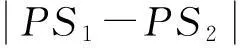振動(dòng)加強(qiáng)點(diǎn)和減弱點(diǎn)判斷的深入分析及從中得到的教學(xué)啟示*
李展華
*系臺(tái)州市2015年教育科學(xué)規(guī)劃研究課題“新考改下校本選修課程與國(guó)家主干課程有效融合的探索——以高中物理學(xué)科為例”研究成果,課題編號(hào):TG15151
(臨海市回浦中學(xué) 浙江 臺(tái)州 317000)
?
振動(dòng)加強(qiáng)點(diǎn)和減弱點(diǎn)判斷的深入分析及從中得到的教學(xué)啟示*
李展華
*系臺(tái)州市2015年教育科學(xué)規(guī)劃研究課題“新考改下校本選修課程與國(guó)家主干課程有效融合的探索——以高中物理學(xué)科為例”研究成果,課題編號(hào):TG15151
(臨海市回浦中學(xué)浙江 臺(tái)州317000)
摘 要:文中對(duì)一道常規(guī)振動(dòng)加強(qiáng)點(diǎn)和減弱點(diǎn)判斷問(wèn)題的解答提出了質(zhì)疑,分別用幾何證明法和定量計(jì)算法做了詳細(xì)的證明,并對(duì)問(wèn)題產(chǎn)生的根源做了深入剖析,最后提出質(zhì)疑精神、探究能力和攻堅(jiān)意識(shí)的培養(yǎng)與提高要先從教師自身做起.
關(guān)鍵詞:加強(qiáng)點(diǎn)減弱點(diǎn)啟示質(zhì)疑探究
1問(wèn)題的提出
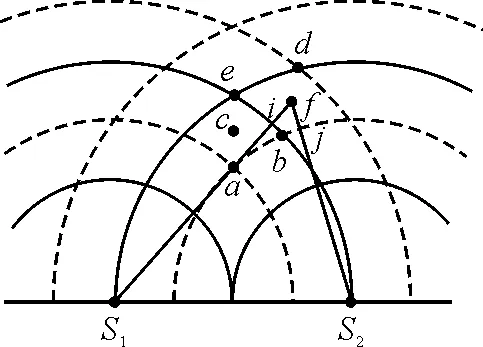
【題目】如圖1表示兩個(gè)相干波源S1和S2產(chǎn)生的波在同一種均勻介質(zhì)中相遇.圖中實(shí)線表示波峰,虛線表示波谷,c和f分別為ae和bd的中點(diǎn),則
(1)在a,b,c,d,e,f6點(diǎn)中,振動(dòng)加強(qiáng)的點(diǎn)是________;振動(dòng)減弱的點(diǎn)是________.
(2)若兩振源S1和S2振幅相同,此時(shí)刻位移為零的點(diǎn)是________.
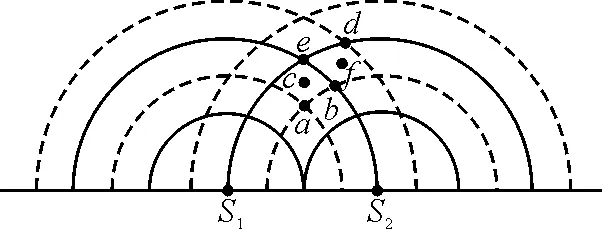
圖1
解析:(1)a和e兩點(diǎn)分別是波谷與波谷、波峰與波峰相交的點(diǎn),故此兩點(diǎn)為振動(dòng)加強(qiáng)點(diǎn);c點(diǎn)處在a和e連線上,且從運(yùn)動(dòng)的角度分析a點(diǎn)的振動(dòng)形式恰沿該線傳播,故c點(diǎn)是振動(dòng)加強(qiáng)點(diǎn).而b和d兩點(diǎn)是波峰與波谷相交的點(diǎn),故此兩點(diǎn)為振動(dòng)減弱點(diǎn);f點(diǎn)處在b和d兩點(diǎn)連線上,也是振動(dòng)減弱點(diǎn).
(2)因?yàn)镾1和S2振幅相同,波峰與波谷相遇時(shí)位移為零,或兩平衡位置相遇時(shí)位移也為零,故此時(shí)刻位移為零的點(diǎn)有b,c,d,f.
答案:(1)a,c,e;b,d,f;(2)b,c,d,f.
考點(diǎn):波的干涉中振動(dòng)加強(qiáng)點(diǎn)和減弱點(diǎn)的判斷方法.
(1)公式計(jì)算法:某質(zhì)點(diǎn)的振動(dòng)是加強(qiáng)還是減弱,取決于該點(diǎn)到兩相干波源的距離之差Δr.當(dāng)兩波源振動(dòng)步調(diào)一致時(shí)
若Δr=nλ(n=0,1,2,…),則振動(dòng)加強(qiáng);
若Δr=(2n+1)(n=0,1,2,…),則振動(dòng)減弱.
(2)現(xiàn)象觀察法:波谷與波谷、波峰與波峰相遇的點(diǎn),為振動(dòng)加強(qiáng)點(diǎn);波峰與波谷相遇的點(diǎn),為振動(dòng)減弱點(diǎn).
絕大多數(shù)復(fù)習(xí)資料對(duì)本題的解析都是如上所述,上面的分析看似順理成章,符合師生的正常思維和邏輯推理,但是深入思考不難產(chǎn)生以下疑惑:
(1)兩相鄰加強(qiáng)點(diǎn)連線的中點(diǎn)一定是處于平衡位置嗎?即此時(shí)刻c點(diǎn)的位移是零嗎?
(2)兩相鄰加強(qiáng)點(diǎn)(或減弱點(diǎn))連線上的其他點(diǎn)一定也是加強(qiáng)點(diǎn)(或減弱點(diǎn))嗎?即c點(diǎn)一定是加強(qiáng)點(diǎn)嗎?f點(diǎn)一定是減弱點(diǎn)嗎?此時(shí)刻f點(diǎn)的位移還是零嗎?
2問(wèn)題的解決
針對(duì)上述的疑惑,下面采用兩種方法進(jìn)行解惑.
(1)幾何證明法
問(wèn)題焦點(diǎn)——疑惑(1)
證明:連接S1和c兩點(diǎn)并與c點(diǎn)附近波源S1產(chǎn)生的波谷、波峰交于g與h兩點(diǎn),再分別過(guò)a和e做S1和c連線的垂線,垂足分別為k和l,如圖2所示.利用平面三角形知識(shí),容易得出△akc≌△elc,故線段kc=線段lc,又gc 圖2 問(wèn)題焦點(diǎn)——疑惑(2) 證明:根據(jù)波的干涉中振動(dòng)加強(qiáng)點(diǎn)和減弱點(diǎn)的判斷方法——公式計(jì)算法,c點(diǎn)位于S1和S2連線的中垂線上,易得c點(diǎn)為振動(dòng)加強(qiáng)點(diǎn). 對(duì)f點(diǎn)的判斷,可進(jìn)行如下操作:連接S1和f,并與S1波在f點(diǎn)附近產(chǎn)生的波峰交于i,連接S2和f,并與S2波在f點(diǎn)附近產(chǎn)生的波谷交于j,如圖3所示. 圖3 f點(diǎn)所處位置不像c點(diǎn)那樣具有很強(qiáng)的對(duì)稱性,故fi≠fj,因而不易得出 S1f-S2f=0.5λ 故f點(diǎn)不是振動(dòng)的減弱點(diǎn),此刻f點(diǎn)的位移不是零. 此處針對(duì)疑惑(2)的證明雖然有些道理,但仍不夠直觀清晰,很難讓讀者徹底地信服,筆者再用定量計(jì)算法對(duì)此加以說(shuō)明. (2)定量計(jì)算法 問(wèn)題焦點(diǎn)——疑惑(2) 證明:取S1和S2連線為x軸,水平向右為x軸正向,以S1和S2連線的中垂線為y軸,豎直向上為y軸正向,取S1和S2連線的中點(diǎn)為坐標(biāo)原點(diǎn)O,建立平面直角坐標(biāo)系,取波長(zhǎng)λ=2,S1和S2坐標(biāo)分別為(-2,0)、(2,0).下面求b點(diǎn)的坐標(biāo),b點(diǎn)是兩圓的交點(diǎn),故b點(diǎn)坐標(biāo)為兩圓相應(yīng)方程的解.由圓的定義,可以得出兩圓的相應(yīng)方程為 (x+2)2+y2=16 (x-2)2+y2=9 解得 S1f=4.491 061 S2f=3.488 499 S1f-S2f=1.002 562 顯然S1f-S2f≠0.5λ,故f點(diǎn)不是振動(dòng)的減弱點(diǎn),此刻f點(diǎn)的位移不是零.至此,疑惑(2)解除.同樣,用定量計(jì)算法也容易對(duì)疑惑(1)進(jìn)行討論,這里不再贅述. 綜上所述,原題答案應(yīng)修正為(1)a,c,e;b,d;(2)b,d. 3問(wèn)題產(chǎn)生的根源 針對(duì)疑惑(2),筆者認(rèn)為產(chǎn)生的根源在于如何進(jìn)行連線的問(wèn)題,是用直線連接,還是用平滑的曲線連接,如果是用平滑的曲線連接,隨意性較強(qiáng),很難準(zhǔn)確分析這個(gè)問(wèn)題.筆者仔細(xì)閱讀了相關(guān)教材[1]及教師教學(xué)用書[2]中的有關(guān)章節(jié),沒(méi)有找到“關(guān)于如何連線”的任何說(shuō)明,這就為錯(cuò)誤的產(chǎn)生埋下了種子.于是,有的教師可能基于考綱中對(duì)此未做要求,便像教材那樣避而不談,留給學(xué)生自己去揣摩;也有的教師淺顯地認(rèn)為加強(qiáng)區(qū)(或減弱區(qū))就是把兩相鄰加強(qiáng)點(diǎn)(或減弱點(diǎn))用直線依次連起而形成的,這種理解從加強(qiáng)區(qū)(或減弱區(qū))的局部看勉強(qiáng)還行,但如果從整體看問(wèn)題就出現(xiàn)了,圖4為一相干波源干涉的示意圖,很顯然,其中任一條加強(qiáng)區(qū)(或減弱區(qū))不是由折線組成的,而是一條較平滑的曲線.那么,我們?nèi)绾胃鶕?jù)已有的幾個(gè)加強(qiáng)點(diǎn)(或減弱點(diǎn))精確描繪出代表加強(qiáng)區(qū)(或減弱區(qū))的平滑曲線呢?這些平滑的曲線有何幾何特征?這里要先從加強(qiáng)區(qū)(或減弱區(qū))的特征談起. 圖4 其中,n=1時(shí)對(duì)應(yīng)距離S1S2中垂線最近的一對(duì)減弱區(qū),n=2時(shí)對(duì)應(yīng)距離S1S2中垂線最近的一對(duì)加強(qiáng)區(qū)……至此,便可以很輕松地寫出圖1中b和d點(diǎn)所在減弱區(qū)的雙曲線方程,只須令上式中n=1,λ=2即可得 再將f點(diǎn)坐標(biāo)代入便可檢驗(yàn)出是否為減弱點(diǎn).讀到這里,大家對(duì)“為何加強(qiáng)點(diǎn)ae連線中點(diǎn)c為加強(qiáng)點(diǎn),而減弱點(diǎn)bd連線中點(diǎn)f卻不是減弱點(diǎn)”應(yīng)該有了更加清晰而深刻的理解吧. 4教學(xué)啟示 明代學(xué)者陳獻(xiàn)章在《論學(xué)書》中說(shuō)過(guò):“前輩學(xué)貴有疑,小疑則小進(jìn),大疑則大進(jìn).疑者,覺(jué)悟之機(jī)也,一番覺(jué)悟,一番長(zhǎng)進(jìn).”有疑有惑,便出現(xiàn)了“心求通而未得之意”,“口欲言而未能之貌”的情形.這說(shuō)明生疑、發(fā)問(wèn)很重要,尤其是能夠在“不疑處有疑”.為何一道常規(guī)習(xí)題的錯(cuò)誤答案能夠流傳至今? 首先表明我們師生質(zhì)疑精神和獨(dú)立思考能力匱乏,大家過(guò)于依賴書本資料,缺乏自己對(duì)問(wèn)題的看法和態(tài)度,更少有去堅(jiān)守自己的學(xué)術(shù)立場(chǎng),教師如此,何況學(xué)生呢?這一點(diǎn)可能與我國(guó)長(zhǎng)期以來(lái)的灌輸式應(yīng)試教育模式有直接的關(guān)系吧. 其次表明我們師生探究能力和攻堅(jiān)意識(shí)不強(qiáng),筆者堅(jiān)信你或是你的學(xué)生一定曾經(jīng)懷疑過(guò)這道常規(guī)習(xí)題的錯(cuò)誤答案,但苦于一時(shí)又說(shuō)不清楚,找不到解決的辦法,便采用了“過(guò)其門而不入”處理方式,其實(shí),這樣的處置方式實(shí)際上是一種浪費(fèi)了極好的教育資源的不妥做法. 在此,筆者要大聲呼吁,質(zhì)疑精神、探究能力和攻堅(jiān)意識(shí)的培養(yǎng)與提高要先從我們教師自身做起,只有如此,我們才能在潛移默化中影響到學(xué)生. 參 考 文 獻(xiàn) 1課程教材研究所.物理·選修3-4.北京:人民教育出版社,2010.33~34 2課程教材研究所.物理·選修3-4教師教學(xué)用書.北京:人民教育出版社,2010.43~44 3薛金星.高中數(shù)學(xué)基礎(chǔ)知識(shí)手冊(cè).北京:北京教育出版社,2008.214~215 收稿日期:(2015-01-01)