基于M-Copula-EGARCH-M-GED模型的相關風險度量及投資組合優化

宗欽原，申建平

(重慶大學數學與統計學院，重慶 401331)

一、引言

相關風險度量和最優組合投資是投資者和資產管理者非常關心的問題。Copula函數是在1959年由Sklar［1］提出的，從90年代開始被應用在金融領域中，Rockinger等［2］提出可以運用 Copula函數建立多變量時間序列模型來替代向量GARCH模型;Patton［3］構造了馬克-美元和日元-美元匯率的對數收益的二元 Copula模型，并與相應的BEKK模型作比較，結果表明Copula能更好地描述金融市場的相關關系;Romano［4］提出應用Copula處理金融的組合風險，同時利用多元函數極值，通過使用Monte Carlo方法來刻畫市場風險;Hu［5］在Gumble、Clayton和FrankCopula函數的基礎上，構建了一種新的Copula函數，即混合Copula函數(M-Copula)，它是以上三種函數的線性組合，權重參數反應變量間的相關程度;韋艷華等［6］利用MCopula與GARCH相結合對金融市場相關程度和相關模式進行了研究;戰雪麗等［7］用Copula-SV模型對投資組合資產的相關風險進行了分析;劉志東［8］運用Copula-GARCH-EVT模型研究了資產投資組合的最優投資比;史道濟等［9］利用Copula函數對股票市場的VaR和最優投資組合進行了分析計算;包衛軍等［10］利用多維的 t-Copula函數，對投資組合的CVaR進行了分析。這些研究表明Copula函數與條件異方差模型相結合是一種較為實用的金融量化分析方法，但存在三點不足:(1)為了減少實證中模型參數估計難度，當前的大部分論文對連接函數Copula的選擇主要集中在Gumble、Clayton 和 FrankCopula 函數中的一種，而 Hu［5］的研究表明單一的Copula函數，對資產間的相關性描述是有局限性的;(2)對單個金融資產收益率的建模，主要以GARCH和EGARCH模型為主，但在現實中存在收益率的風險調整和風險補償，而這兩個模型不能刻畫這一特征;(3)利用Copula和條件異方差模型進行最優組合計算之前，沒有對VaR和CVaR的計算結果進行有效性檢驗。

因此，本文構建了能刻畫風險溢價的EGARCH-M模型，對各單個資產收益率進行建模，選用M-Copula作為聯合分布函數，用遺傳算法對模型中參數進行計算，用基于GED分布的CVaR度量風險，最終利用Monte Carlo方法模擬求得不同投資比例和置信水平下的VaR和CVaR值，求出不同期望收益和置信水平下的最優組合投資權重。.實證表明，該建模方法效果良好，能有效地解決Copula函數與條件異方差模型相結合存在的不足。

(一)Copula函數的相關理論

定理 1.1(Sklar定理)［1］令 H(·，·)為具有邊緣分布函數F(·)和G(·)的聯合分布函數，那么存在一個 Copula函數 C(·，·)，滿足:

H(x，y)=C(F(x)，G(y)) (1)若 F(·)和 G(·)連續，則 C(·，·)唯一確定;反之，若 F(·)和 G(·)為一元分布函數，C(·，·)為相應的Copula函數，那么由式(1)定義的函數H(·，·)是具有邊緣分布F(·)和G(·)的聯合分布函數。

Gumble、Clayton和FrankCopula函數是三類常用的二元阿基米德Copula函數，以下簡要介紹他們在相關性分析中的應用特點。

(1)Gumble Copula 函數［11-12］的分布函數和密度函數分別為:

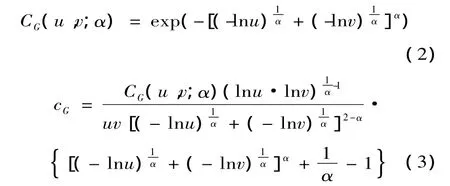
Gumble Copula函數的密度函數具有非對稱性，其密度分布呈“J”字形，即上尾高，下尾低。分布函數對分布變量在分布上尾部的變化十分敏感，能夠快速地捕捉到上尾相關的變化，而在分布的下尾部，由于變量是漸進獨立的，函數對變量在分布下尾部的變化不敏感，難以捕捉到下尾的相關的變化。

(2)Clayton Copula 函數［11-12］的分布函數和密度函數分布為:

Clayton Copula的密度函數具有非對稱性，其分布呈“L”字形，即上尾低，下尾高。故函數對變量在分布下尾的變化十分敏感，能夠快速捕捉到下尾相關的變化，而在分布的上尾部，由于變量是漸進獨立的，其上尾的變化不敏感，難以捕捉到上尾的相關的變化。

(3)Frank Copula 函數［11-12］可以描述變量間的負相關關系，它的分布函數和密度函數分布為:

其中，λ為相關參數，λ≠0。λ＞0表示隨機變量u、v正相關，λ→0表示隨機變量u，v趨向于獨立，λ＞0表示隨機變量u、v互相關。Frank Copula的密度分布呈“U”字形，具有對稱性，因此無法捕捉到隨機變量間非對稱的相關關系。因此此函數只適合于描述具有對稱相關結構的變量之間的相關關系。

(二)M-Copula函數的構建

用前面三者的線性組合來構建混合Copula函數，記作 M-Copula 函數［13］，其表達式為:

其中 wC，wCl，wF≥0，wG+wCl+wF=1。對應的密度函數為:

MC3表示由三個Copula函數的線性組合組成的混合 Copula 函數，CG、CCl、CF分別表示 Gumble、Clayton 和 Frank Copula 函數，wC，wCl，wF為相應的Copula函數的權重系數。由式(2)、(4)、(6)、(8)可知，MC3包含六個參數，其中的相關參數向量(α，θ，λ)可以度量變量之間的相關程度，而線性組合的系數即權重參數向量(wG，wCl，wF)則反映變量之間的相關模式。

由此而見，可以用M-Copula來描述具有各種模式的變量之間的相關關系，與單個Copula函數相比更為靈活，能夠描述具有復雜相關關系的事物，如金融市場之間的相關關系，因此，本文采用應用更為廣泛、使用性也更強的M-Copula函數來描述深市和上市兩者間的相關性。

二、M-Copula-EGARCH-M-GED模型的建立

(一)EGARCH-M模型的建立

Nelson［14］提出了指數 GARCH(EGARCH)模型，它能夠充分捕獲高頻金融時間序列的尖峰厚尾性。EGARCH(p，q)模型形式為

這里，正的εt-i對對數波動率的貢獻為αi+γi，而負的 εt-i對對數波動率的貢獻為 αi- γi，參數γi表示 εt-i的杠桿效應。Engle、Lilien 和 Robins將基本的ARCH模型加以擴展，允許序列的均值不獨立于條件方差，這類模型被稱為ARCH-M模型，其基本觀點是風險厭惡的投資者會在持有風險資產時要求相應的風險補償。由于一項資產的風險可以用收益的方差來衡量，風險溢價就是收益條件方差的增函數［15］。將持有一項有風險資產所帶來的超額收益描述為

其中，yt表示持有金融資產所帶來的超額收益率;μt代表足以使風險厭惡的投資者持有金融資產的風險溢價;εt表示對金融資產收益率的不可預測的沖擊。而持一項長期金融資產收益必須恰好等于風險溢價［16］，也就是說

假設風險溢價是εt的條件方差的增函數，即，收益率的條件方差越大，使投資者持有長期資產所需的風險溢價就越大。即，如果σ2t是 εt的條件方差，則風險溢價就可以表述為

其中，μi為收益率的無條件期望值，系數δi反映了風險和收益之間的替代關系，即為風險溢價參數，εi.t為擾動為隨時間變化的的條件方差，ηi，t為獨立同分布的標準殘差，αi為滯后參數，βj為方差參數。常用γi來說明金融市場中價格的非對稱影響，當γi≠0時，說明各種干擾對價格的影響是非對稱的;當γi＜0時，說明價格波動受負外部沖擊的影響大于受正外部沖擊的影響;當γi＞0時，正的外部沖擊大于負的外部沖擊，此種現象稱之為“杠桿效應”。

(二)M-Copula-EGARCH-M-GED模型的建立

假設標準殘差 ηt=(η1，t，η2，t)獨立同分布，t=1，2，3，…，T，其聯合分布函數為 G(z1，z2)，邊際分布函數分別為Fi(zi)，i=1，2。為了更加靈活地刻畫變量之間的相關關系及序列間的相關結構，采用M-Copula函數建模，建立M-Copula-EGARCHM-GED模型:

(三)M-Copula-EGARCH-M-GED模型的參數估計

上述模型(15)的參數估計包含兩部分，一部分是EGARCH模型的參數，另一部分是M-Copula的相關參數，本文采用兩步極大似然估計進行參數估計。首先EGARCH模型的參數通過極大似然估計去獲得，相應得到標準誤差 ηi，t的估計，然后對 M-Copula的相關參數采用遺傳算法進行估計。

(四)M-Copula-EGARCH-M-GED模型檢驗

1.M-Copula函數的擬合度檢驗

Hu［5］在研究歐美外匯與股票市場相關關系時，采用一個服從χ2分布的M經驗統計量來評價Copula函數的擬合優度，從而確定選定的Copula函數是否適合，其具體步驟如下。

令{ut}和{vt}，t=1，2，…，T，都是服從 i.i.d.(0，1)均勻分布序列，它們是根據估計得到的邊緣分布，對觀測序列{xn}和{yn}，t=1，2，…，T 進行概率積分變換之后得到。構造一個包含k×k個單元格的表格G，表格中處于第i行、第j列的單元格記作G(i，j)，表示一個下界為，上界為的概率組合，其中k的選取可以根據樣本的總數和觀測點的總數來確定，既要保證有足夠多的單元格用于模型擬合度的評價，又要保證每個單元格中都有足夠的觀測點。對于任何一點，若，則點(ut，vt)∈G(i，j)，若用 Ai，j表示落在單元格 G(i，j)內的實際觀測點個數，用Bi，j表示由Copula模型預測得到的落在單元格G(i，j)的點的個數，即預測頻數，其中 i，j=1，2，…，k，則評價 Copula 函數擬合度的χ2檢驗統計量M可表示為

其中統計量M服從自由度為(k-1)2的χ2分布。

2.EGARCH-M模型的檢驗

為了驗證 EGARCH-M的合理性，本文采用Ljung-Box Q檢驗法［17］對EGARCH-M模型的殘差序列的相關性進行檢驗，利用K-S檢驗法［17］對EGARCH-M模型誤差分布的擬合度進行檢驗。

三、基于M-Copula-EGARCH-M-GED模型的CVaR計算和投資組合優化

定義 2 CVaR(Conditional Value at Risk)，即條件期望值，是繼VaR之后產生的一種風險度量方法。根據 Rockafella［18］的定義，CVaR 是指在一定的置信水平下，某一資產或資產組合的損失超過VaR的尾部事件的期望值。CVaR用數學公式可以定義為

其中，α為置信水平;w為資產或資產組合的價值;f(w)為概率密度函數;VaRα為置信水平α的風險值。

利用M-Copula計算CVaR時，運用蒙特卡洛模擬需要構造二維的隨機向量(X，Y)的隨機數，若已知X，Y的邊際分布函數F1(x)和F2(x)，設其M-Copula函數為C(u，v)，令 U=F1(x)并且 V=F2(x)，則 U，V 都服從［0，1］上的均勻分布，由Copula函數的性質可知，在給定 U=u∈［0，1］為固定值時，隨機變量 V對 u的條件分布函數在v∈［0，1］內是單調非減，若令k=Cu(v)，則k服從［0，1］上的均勻分布，從而，我們可以得到隨機數u和k，然后可以根據條件分布函數Cu(v)的反函數求得另一個隨機數v=，這樣就可以構造偽隨機數對(u，v)。若金融資產為，就可得到隨機數對(x，y)，經過n次的模擬我們可得到n組模擬的收益率數對(xi，yi)，i=1，2，…，n。由此我們獲得了n個投資組合收益率的模擬數zi=wxi+(1-w)yi，再對{zi}，i=1，2，…，n 由小到大進行排序，排序后的序列不妨設為{si}，則在置信水平為1-α時:

(一)MonteCarlo模擬方法的算法步驟

本文進行MonteCarlo模擬計算VaR和CVaR，主要目的是驗證所建模型對風險的預測能力，以便使相關風險最小化的最優投資組合比更具實在價值。

假設金融資產組合有兩種資產X和Y，其收益率分別為x，y，組合中他們所占的比例分別為ω和1-ω，則資產的總收益率為ωx+(1-ω)y。

(1)根據我們選取的M-Copula函數做Monte-Carlo［19］模擬，模擬6 000 個數據，則我們得到6 000個隨機數據對{(un，vn)}，n=1，2，…，6 000，則(un，vn)～ C(u，v)。

(2)設兩列標準殘差序列的分布函數為標準GED 分布 Fη1和 Fη2，對每一組數據對(un，vn)，我們令，可得到標準殘差序列{(η1，n，η2，n)}。

(3)運用Eviews對EGARCH模型進行參數估計時可得到兩個均值為和兩列條件異方差序列，取1，…，T，我們有為6 000維的列向量i=1，2。

(4)由于我們所分析的收益率為對數收益率rt=lnpt-lnpt-1，用Rt=pt/pt-1-1來將其正常收益率形式，則Rt=ert-1，由此對第k次模擬我們可以得到正常的組合收益率Rt=ω(er1，k-1)+(1-ω)(er2，k-1)，Rk也為 6 000 維的列向量。

(5)我們對(4)中Rk得到的6 000個數進行升序排列，則對置信度(1-α)，我們取第6 000×α+1個數的絕對值即為相關置信度的VaR，對前6 000×α個數求算術平均值后為相應置信度的CVaR。

為了對所估算VaR和CVaR的值進行效果檢驗，本文選用DLC的返回檢驗，而DLC表示實際損失的期望值與CVaR的期望值之差的絕對值，定義如下:

(二)基于最小化CVaR建立最優投資組合模型

與VaR相比，CVaR滿足次可加性、正齊次性、單調性及傳遞不變性，因此可以將CVaR作為風險指標［20］，通過使用線性規劃來進行優化;陳科燕［21］應用遺傳算法對最優證劵投資組合模型進行研究;Rackafellar［20］利用CVaR作為風險指標來討論資產組合最優化問題。考慮到中國市場的不允許賣空，因此在下面模型中我們加入了不允許賣空的限制。假設市場有n個風險資產，ri為投資期內風險資產i的收益率，wi為投資者在風險資產i上的投資比例。那么組合收益率可以表示為

以CVaR來測度投資風險，損益服從廣義誤差分布(GED)的CVaR的計算公式:

其中K＞0，為投資者最低預期收入水平，β為置信度。

四、實證分析

(一)數據選取及其基本分析

本文選取樣本數據為1998年9月28日到2012年3月23日中國股票市場上的上證綜指與深證成指的收盤價，總樣本數目為3 260個，通過公式rt=lnpt-lnpt-1計算兩個指數的收益率。本文使用的軟件為Eviews 6.0和MatlabR 2010a進行計算。

由圖1和圖2我們可以看出上證綜指和深證成指的收益率具有波動率聚集性，與金融時間序列的特征吻合。另一方面從整體來看，兩者收益率的波動性都很劇烈，說明對股票市場的風險管理的必要性。

圖1 上證綜指的收益率

圖2 深證成指的收益率

圖3與圖4分別為上證綜指和深證成指對數收益率序列的基本統計量，可以看出上證綜指與深證成指對數收益率序列具有以下特征:(1)樣本峰度都遠大于3，表明上證綜指與深證成指對數收益率呈現明顯的尖峰厚尾性;(2)Jarque-Bera正態統計量的值遠大于臨界值5.99，表明序列的分布不是正態分布;(3)波動具有聚集性和左偏性。

(二)EGARCH-M-GED模型參數估計

使用EGARCH-M-GED模型對兩個指數收益率序列的邊緣分布進行建模，其殘差服從GED(廣義誤差分布)，其模型的估計結果見表1、表2。

圖3 上證綜指收益率序列的基本統計量圖

圖4 深證成指收益率序列的基本統計量圖

表1 上證綜指收益率序列參數估計結果

表2 深證成指收益率序列參數估計結果

由表1和表2知，(1)γi都小于0，在上證綜指中(表1)為 -0.028 008，深證成指中(表2)為-0.019 015，而且都是顯著的，這也說明了兩市中都存在杠桿效應，即壞消息引起的波動要比同等大小的好消息引起的波動要大;(2)模型估計αi均大于0，說明股市波動呈現集聚現象，過去的擾動對未來的波動有著正面的影響，較大幅度的波動后面緊跟著較大幅度的波動，股市參與者的投機性較強;(3)αi+βi都稍微大于1，則衰減速度越慢，波動的持續性越強，說明在模型下的當前信息對預測未來的條件方差都很重要;(4)滬深兩市均值方程中的條件方差項GARCH的系數估計分別為3.850 810和5.048 627，而且都是顯著的，這反應了收益與風險正相關，說明收益有正的風險溢價，深圳股市的風險溢價要高于上海，深圳股市的投資者更加厭惡風險，要求更高的風險補償。

標準化殘差{ηi，t}的Ljung-Box統計量為統計量為Q(10)=11.38，p值為0.33。因此，在5%的顯著水平下，式(14)的EGARCH-M模型能充分地描述給定數據的條件異方差性。

(三)M-copula函數的參數估計

利用EGARCH-M-GED模型中得到的兩個標準殘差序列對混合Copula函數的參數進行極大似然估計，估計方法是遺傳算法［22］，在 MatlabR 2010a環境中編程完成。如表3所示。

表3 Copula函數的參數估計結果

擬合統計量M的值說明了:copula函數選取的不同，對兩個市場指數收益率相關程度與相關模式的刻畫能力相差非常大，M-copula函數對樣本的擬合度是最好的，其次就是Gumble copula函數，剩下的兩個copula函數擬合度相對較差。

比較圖5、圖6、圖7、圖8可知，GumbleCopula函數分布低估下尾的相關程度，明顯高估了上尾的相關程度;ClaytonCopula函數分布明顯低估上尾的相關程度;和FrankCopula函數分布不僅低估上下尾相關程度，而且不能反映兩個市場的非對稱的相關模式;M-copula的分布函數最接近經驗聯合分布，能夠比較全面和準確地捕捉各個時期上海和深圳股票市場之間相關程度變化，且能夠正確地反映兩個市場之間非對稱的相關模式。

圖5 Gumble

圖6 Clayton

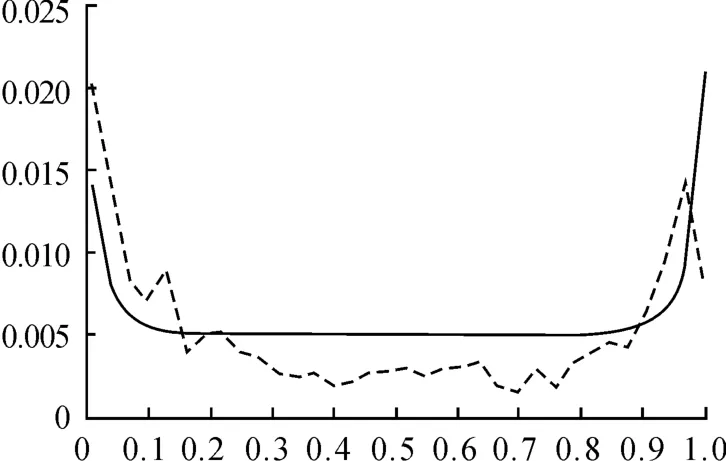
圖7 Frank

圖8 M-Copula

以上為經驗聯合分布和4類Copula函數分布在u=v處的頻率分布圖(實線指Copula函數分布，虛線指經驗聯合分布)

(四)VaR和CVaR的Monte Carlo模擬計算及分析

圖9為用歷史數據通過模型擬合而成的上證綜指和深證成指的相關離散點圖，圖10為通過模型對兩個市場的T+1時刻預測的6 000個數據的離散點圖，兩圖說明模型能對未來的兩市場的相關性變動進行合理正確的預測。下面我們將對歷史數據的風險值和模型預測的風險進行比較，以便說明本文所建模型對相關風險預測的準確性。

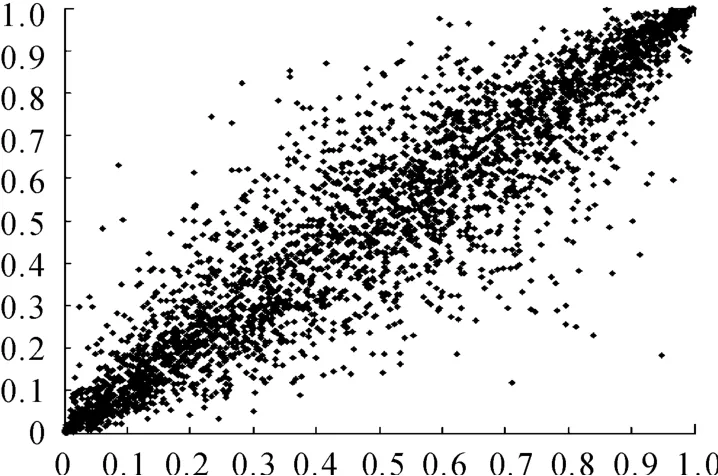
圖9 相關離散點圖

圖10 離散點圖

由表4-6可知，置信水平1-α=0.99或者1-α=0.95，VaR都比較接近 α，表現相當不錯，但還是具有一定激進性;而通過統計量DLC，我們可以看到CVaR對風險的度量比較好。下面我們將對CVaR最小化為目標函數，進行投資組合的最優化的計算結果。

由表7可知，用模型對時間點T+1的收益率進行預測，知上證綜指的平均收益率為0.000 6，深證成指平均收益率為0.001 4，但在5%的分位數下，上證綜指和深證成指的CVaR分別為0.039 6和0.023 4，由于上證綜指的收益率小且條件風險值大，故在分位數為5%時，要使在固定收益CVaR最小，只有將資金絕大部分投入深圳證劵市場;而當分位數取10%時，上證綜指和深證成指的CVaR分別為0.030 7和0.069 6，顯然深證成指的條件風險值遠遠大于上證綜指，故資金在收益率低時，應將其大部分投放在上海證劵市場，隨著收益率的升高，上海市場的投資比例降低，深證市場的資金比例上升，同時CVaR的值升高，符合高風險高收益，但是對二者的固定收益率超過13%時，最優解將不存在，與金融市場的多變性吻合。通過本模型，我們可以通過對不同分位數的選擇來擴大風險范圍，增加收益，來對不同風險厭惡程度的投資者進行投資指導，使得風險得到有效管理。

表4 數據總數為3 258個，投資比例w=1/3的模擬數據統計結果

表5 數據總數為3 258個，投資比例w=1/2的模擬數據統計結果

表6 數據總數為3 258個，投資比例w=3/4的模擬數據統計結果

表7 下表為分位數為5%和10%，固定收益率下的最優投資比例

五、結論與展望

通過上面的模型分析，本文得出以下結論:

(1)上海和深圳股票市場的收益率均存在明顯的波動集聚性、條件異方差性和杠桿效應，模型估計αi均大于0，說明股市波動呈現集聚現象，過去的擾動對未來的波動有著正面的影響，較大幅度的波動后面緊跟著較大幅度的波動，股市參與者的投機性較強;而αi+βi都稍微大于1，即衰減速度越慢，波動的持續性越強。

(2)滬深兩市均值方程中的條件方差項GARCH的系數估計分別為3.850 810和5.048 647，而且都是顯著的，這反應了收益與風險正相關，說明收益有正的風險溢價，深圳股市的風險溢價要高于上海，深圳股市的投資者更加厭惡風險，要求更高的風險補償。

(3)M-copula函數對樣本的擬合度是最好的，其分布函數最接近經驗聯合分布，不僅能夠比較全面和準確地捕捉各個時期上海和深圳股票市場之間相關程度變化，而且能夠正確地反映兩個市場之間非對稱的相關模式;其次就是Gumble Copula函數，剩下的兩個 copula函數擬合度相對較差。

(4)在分位數為5%時，要獲得固定收益，同時CVaR最小，需將資金絕大部分投入深圳證劵市場;在分位數取10%時，目標收益率較低時，應將其大部分投放在上海證劵市場，目標收益率較高時，上海市場的投資比例應降低，深證市場的資金比例應上升，同時CVaR的值升高，符合高風險高收益。

(5)當二者的目標收益率超過13%時，最優解將不存在，與金融市場的多變性穩合。通過本模型，我們可以通過對不同分位數的選擇來擴大風險范圍，增加收益，來對不同風險厭惡程度的投資者進行投資指導，使得風險得到有效管理;在置信水平1-α=0.99或者1-α=0.95，風險值VaR都比較接近α，表現相當不錯，但還是具有一定激進性，而CVaR對風險的度量比較好。

由于本文主要是對二元資產進行了建模，所以下一步我們可以將這一模型擴展到多元的情況。

［1］Sklar A.Functions derepartition an dimensions leurs marges［J］.Publ.Inst.Paris，1959(8):9-13.

［2］Rockinger M，Jondeau E.Conditional dependency:an application of copula［Z］.Department of Finance，HEC School of Management，Paris，2001.

［3］Patton A J.Modeling time-varying exchange rate dependence using copula［Z］.Department of Economics，University of California，San Diego，2001.

［4］Romano C.Applying copula function to risk mangement［J］.Working Paper of University of Rome“LaSapienza”，2002(1):1-11.

［5］Hu L.Essays in Economics applications in macroeconomic modelling［D］.New Haven:Yale University，2002.

［6］WEI Yan-hua，ZHANG Shi-ying.GUO Yan.Research on degree and patterns of dependence in financial markets［J］.Journal of Systems Engineering，2004(19):355-362.

［7］ZHANG Xue-li，ZHANG Shi-ying.Risk Analysis of Financial Portfolio Based on Copula-SV Model［J］.Journal of Systems ＆ Management，2007，16(3):302-306.

［8］LIU Zhi-dong.A Portfolio Selection Model on Copula-GARCH-EVT Based and Its Hybrid Genetic Algorithm［J］.Systems Engineering-Theory Applications，2006，15(2):149-157.

［9］SHI Dao-ji.LI Fan.Research on the VaR and optimal portfolio of stock markets based on Copula［J］.Journal of Tianjin University of Technology，2007，23(3):54-60.

［10］BAO Wei-jun，XUE Cheng-xian.CVaR analysis based on multidimensional the function of t-Copula portfolio［J］.Statistics and Decision，2008(15):40-45.

［11］Frees E W，Valdez E A.Understanding relationships using Copula［J］.North American actuarial journal，1998，2(1):11-25.

［12］Patton A.Skewness，Asymmetric dependence，and portfolios［Z］.London:London School of Economics＆ Political Science，2002.

［13］WEI Yan-hua，ZHANG shi-ying.Copula theory and its in financial analysis［M］.Beijing:Tsinghua University press，2008:80-85.

［14］Nelsen D B.Conditional in asset returns:A new approach［J］.Econometrica，1991(59):347-370.

［15］Blanchard，Oliver，Danny Quah.The Dynamic Effects of Aggregate Demand and Supply Disturbances［J］.American Economic Review，1989，79:655-673.

［16］Bollerslev T.Generalized autoregressive conditional［J］.Journal of Economics，1986(31):9-20.

［17］WANG Chun-feng.The risk management of financial［M］.Tianjin University press，2001.

［18］Rockafeller，Alexander S.Minimizing CVaR and VaR for a portfolio of derivatives［J］.Journal of Banking ＆ Finance，2006，48:583-602.

［19］XUE Zhong-ji.Monte Carlo method［M］.Shanghai:Shanghai science and technology press，1985.

［20］Rockafeller T，Urvasev S.Conditional value-at-risk for general loss distribution［J］.Journal of Banking ＆ Finance News，2000，2(3):1-5.

［21］CHEN Ke-yan.The Research of the Optimal Model for Portfolio Investment bases on Genetic Algorithm［J］.Journal of Nanjing Institute of Meteorology，2003，26(5):72-81.

［22］WANG Xiao-ping，CAO Li-xin.Genetic Algorithm theory and software realization［M］.Xi’an:Xi’an jiaotong University press，2002:56-78.