軍事逆向物流網絡優化模型及算法研究

趙方庚

(蚌埠汽車士官學校，安徽 蚌埠233011)

1 引言

軍事逆向物流，是指在平戰時，從軍事力量手中回收不合格或者失去原軍事使用價值的軍用物資，為滿足一定的軍事需求，從軍事消費點一端返回并加以適當處理，直至最終完成再利用所進行計劃、管理和控制的過程［1］。軍事逆向物流的網絡結構不僅直接影響資源的回收利用，還關系到軍事物流保障的效率和效益，科學、合理的網絡結構是系統高效運行的重要保證。

隨著人們對環保問題的日益關注，軍事逆向物流也逐漸成為相關領域的研究熱點，但現有研究主要針對軍事逆向物流的運作模式［2］、運行機制［3］和管理措施［4］等問題進行定性的分析，基本沒有涉及軍事逆向物流的網絡優化問題。在民用領域，逆向物流網絡優化得到了相對較多的關注。王亞楠等［5］通過建立物流逆向配送網絡關系的數學模型，利用雙向反饋信息加權算法進行網絡配送優化計算，達到了提高網絡運行效率的目的;高陽和劉軍［6］在考慮產品回收量和消費市場需求量不確定的條件下，以第三方物流企業收益和制造商收益最大化為目標，建立了基于第三方回收多周期再制造逆向物流網絡模型;吳洪波和謝夢星［7］以各種設施的投資和運營成本之和最小為優化目標建立了隨機規劃模型，確定了網絡中各設施的數量和位置，并對各條路徑上的物流量進行了合理分配;王雁鳳和黃有方［8］構建了基于雙層規劃的過期藥品逆向物流網絡優化模型，并設計了求解該模型的分層遺傳算法;Pishvaee 等［9］以運輸和開設成本為優化目標，建立多階段逆向物流網絡的混合整數規劃模型，并研究了其模擬退火算法;Niknejad 和Petrovic［10］建立了包括產品回收過程的庫存與生產規劃優化模型，并提出了求解問題的兩階段模糊混合整數優化算法;Roghanian 和Pazhoheshfar［11］建立了逆向物流網絡的隨機混合整數規劃模型，并研究了基于優先級的遺傳算法。上述研究雖對商業逆向物流網絡建設有較強的指導作用，但都以經濟效益為優化目標，無法適用于軍事逆向物流環境。此外，在基本逆向物流網絡優化算法方面，Pishvaee等［9］應用的模擬退火算法雖取得了較好的優化結果，但在組合優化領域，模擬退火算法并不是最高效的智能優化方法，其計算效率仍有一定的提高空間。基于此，本文建立了軍事逆向物流網絡優化的數學模型，并研究了求解模型的遺傳算法。

2 軍事逆向物流網絡優化模型

2.1 問題描述

本文以軍事逆向物流中的常見形式裝備維修保障為例，研究其逆向物流網絡優化問題。裝備維修逆向物流是一個多階段物流網絡問題(如圖1 所示)，其網絡節點由部隊用戶、收集/檢測點、維修點和報廢點組成。其中，收集/檢測點負責從部隊用戶處收集故障裝備或器材，經過必要的檢測后，將故障裝備或器材分為可修復件和不可修復件;然后可修復件被送往維修點進行維修，不可修復件則送往報廢點進行相應的報廢處置。問題中，收集/檢測點、維修點和報廢點均有能力約束。逆向物流網絡優化的目的是選擇合適的收集/檢測點，并確定網絡中各節點間的裝備或器材流量。

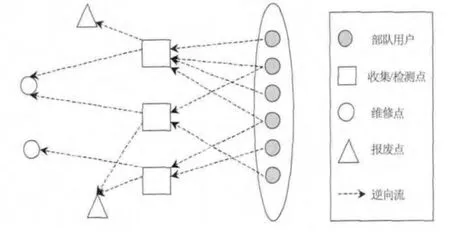
圖1 裝備維修逆向物流網絡結構示意圖

為簡化研究，在模型中作如下假設:①從部隊用戶返回的所有裝備或物資都必須收集;②部隊用戶的位置固定且已知;③維修點、報廢點的數量、位置和能力已知。

2.2 數學模型

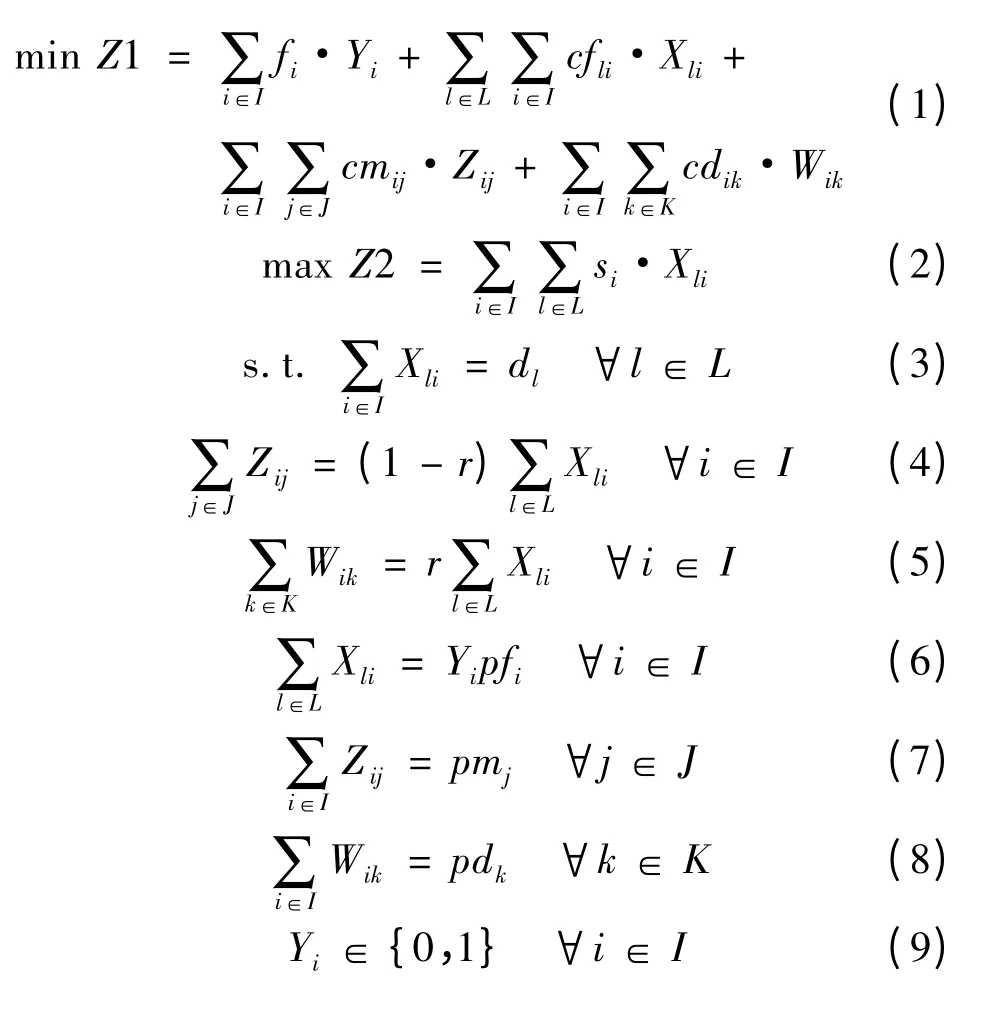
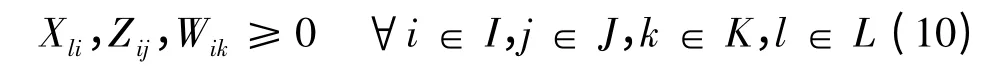
模型中參變量及符號定義為:I為候選收集/檢測點集合;J為已知的修理點集合;K為已知的報廢點集合;L為已知的部隊用戶集合;r為平均報廢率;dl為部隊用戶l返回的物資數量;fi為開設收集/檢測點i的固定成本;si為收集/檢測點i的安全系數;cfli為從部隊用戶l到收集/檢測點i的單位運輸成本;cmij為從收集/檢測點i到維修點j的單位運輸成本;cdik為從收集/檢測點i到報廢點k的單位運輸成本;pfi為收集/檢測點i的能力約束;pmj為維修點j的能力約束;pdk為報廢點k的能力約束。Xli為從部隊用戶l到收集/檢測點i的返回物資數量;Zij為從收集/檢測點i到維修點j的可修件數量;Wik為從收集/檢測點i到報廢點k的不可修件數量;Yi為變量，如果在位置i開設收集/檢測點，則Yi =1，否則Yi =0。

模型中，目標函數(1)為最小化逆向物流系統的總經濟成本，其中第一項為收集/檢測點的開設成本，第二項為物資從部隊用戶到收集/檢測點的總運輸成本，第三項為可修件從收集/檢測點到維修點的總運輸成本，第四項為不可修件從收集/檢測點到報廢點的總運輸成本;目標函數(2)為最大化系統的軍事效益，使系統中物資的安全性最大;約束(3)用以確保部隊用戶返回的所有物資都被收集;約束(4)和(5)用以保證收集/檢測點的流量平衡;約束(6)用以確保部隊用戶返回的物資只被送往開設的收集/檢測點，且不超過收集/檢測點的能力限制;約束(7)和(8)用以保證送往維修點和報廢點的物資數量均不超過它們的能力限制;約束(9)和(10)定義了變量的取值范圍。

在上述軍事逆向物流網絡優化模型中，目標函數(2)是求安全性的最大值，為便于計算，在不影響優化效果的前提下，可將該目標修改為求目標函數最小值的情況:

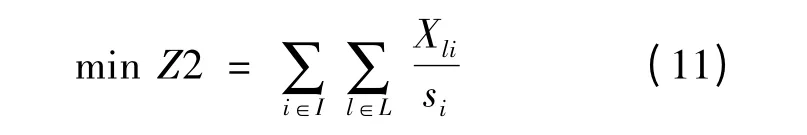
對上述多目標優化模型，本文采用如下方法將之轉化為單目標優化模型:

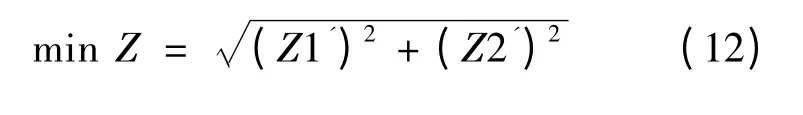
3 軍事逆向物流網絡優化模型的優化算法

由前可知，軍事逆向物流網絡優化模型是一個混合整數規劃模型，變量、約束眾多，傳統的精確算法求解規模較大的此類問題時效率較低，難以滿足解決實際問題的需要。為此，本文采用遺傳算法對問題進行求解。

3.1 算法流程

應用遺傳算法求解軍事逆向物流網絡優化問題首先初始化所用到的參數;然后生成pop_size 個可行解構成初始種群，并對各可行解進行適應度評估;接著利用各遺傳操作算子進行迭代搜索，直到滿足預定的終止條件算法結束。在每步迭代過程中，算法按照輪盤賭策略從種群中隨機地選擇兩個個體，并將個體進行交叉和變異，得到新的子個體。上述遺傳操作過程將進行pop_size/2 次，得到的子個體在進入種群的同時，種群中較差的(適應度低的)個體將被淘汰，以保持種群規模不變。在每次迭代的最后，算法還將在種群中的最佳個體上應用局部搜索過程，以加速算法收斂。另外，算法的終止規則設定為迭代固定的次數。

3.2 染色體表示及解碼方法

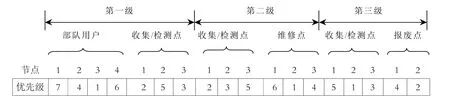
圖2 染色體表示示例

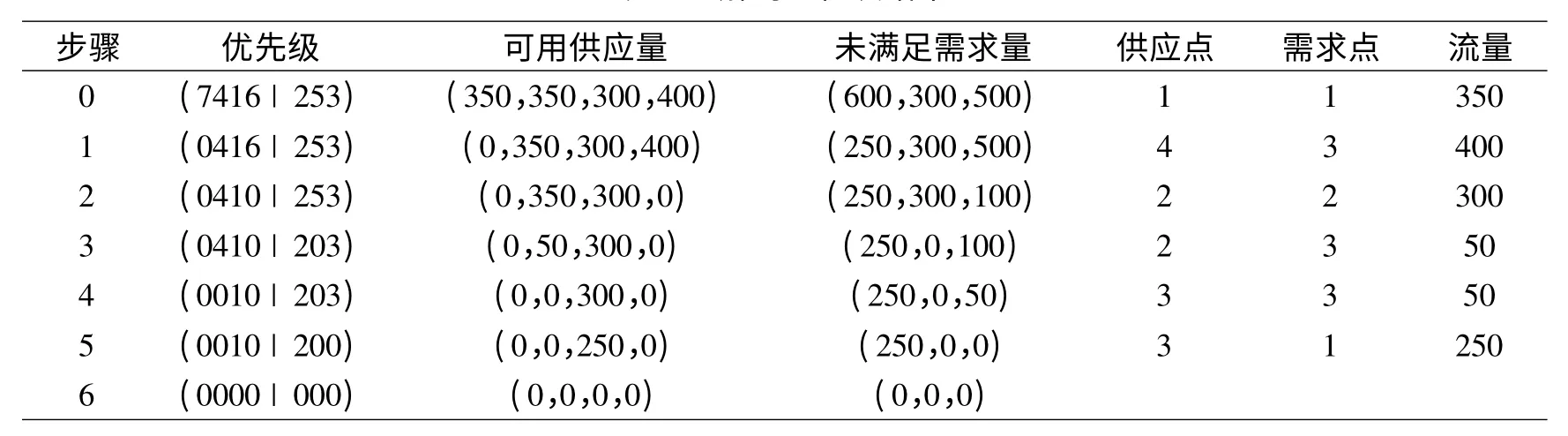
表1 解碼過程及結果

本文采用基于優先級的編碼方法構造軍事逆向物流網絡優化模型的解。染色體由［L］+3［I］+［J］+［K］個正整數組成，其中［L］、［I］、［J］、［K］分別表示部隊用戶、候選收集/檢測點、維修點和報廢點的數量，各數字則分別表示對應節點的優先級。圖2 所示為一染色體示例，該示例由4 個部隊用戶、3 個候選收集/檢測點、3 個維修點和2 個報廢點組成。染色體分為三部分，第一部分表示部隊用戶和候選收集/檢測點之間的物資供給關系，第二部分表示候選收集/檢測點與維修點間的物資供給關系，最后一部分則表示候選收集/檢測點與報廢點間的物資供給關系。

對于上述基于優先級的染色體表示方法，需要將之進行解碼，以獲得各節點之間的物資供給關系。為便于說明，以圖3 所示的單級染色體為例，介紹其解碼方法。圖3 中，(a)為染色體編碼，(b)為供應方和需求方之間的運輸成本，(c)為供需量及解碼后得到的物資供給關系(箭頭表示流向，其上數字表示流量)。具體解碼過程為:首先選擇優先級最高的節點，圖3(a)中對應為節點(供應節點1);然后查找成本矩陣，找出該節點向對應最低運輸成本(min{13，17，16}= 13)所指向的節點(需求節點1);再根據兩個節點的供需量，在二者之間安排最大可能的物資供給(min{350，600}=350);繼續在染色體中尋找次高的優先級，并按上述過程安排物資流。如此反復，直至所有需求都得到滿足，即完成解碼過程。圖3 所示算例，其解碼運算過程及結果見表1。

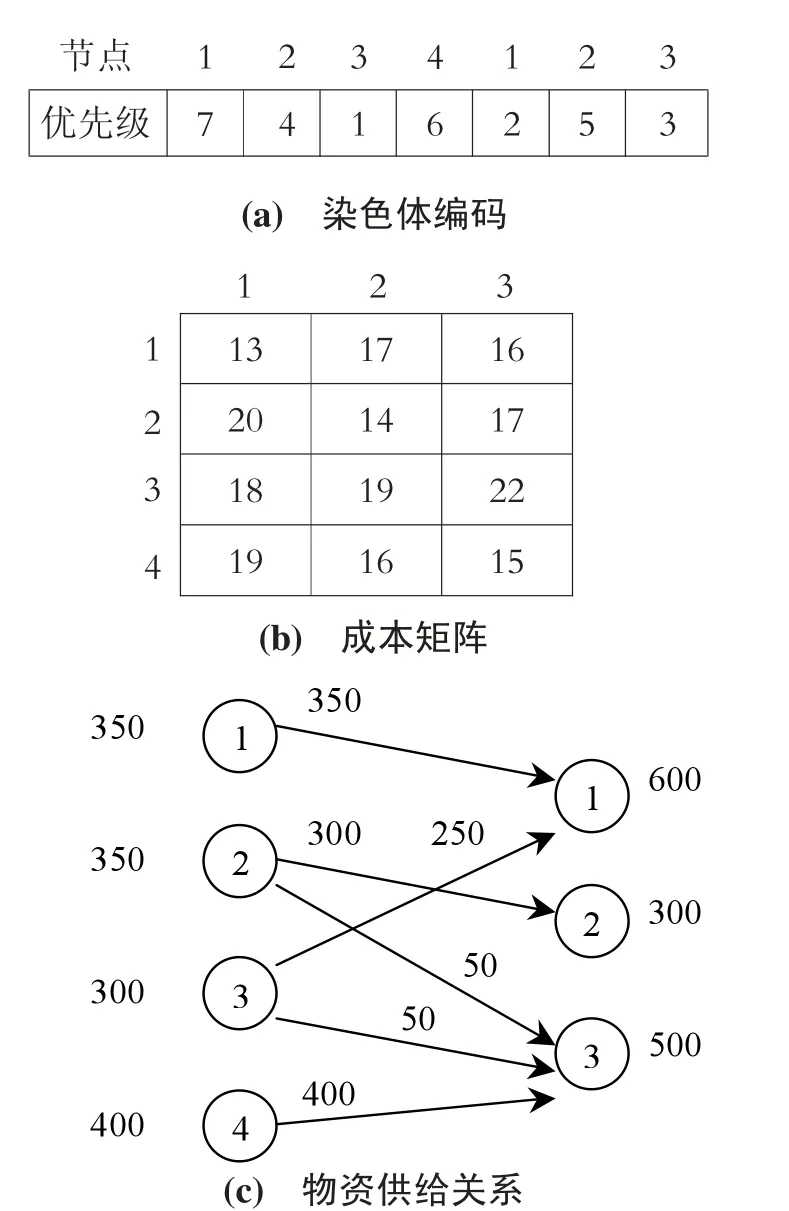
圖3 染色體解碼方法示意圖

3.3 適應度評估及初始種群的生成

染色體的適應度反映了其所表示的解的質量。在本文算法中，公式(12)所定義的目標函數被用于評價染色體的適應度。

初始種群中的個體均采用隨機生成的方法，即對染色體中的各級分別隨機生成長度為［L］+［I］、［I］+［J］和［I］+［K］的數字串，經解碼算法運算后，計算相應的適應度值。

3.4 交叉算子

選擇算子得到的兩個父代個體將進行交叉，以產生新的子個體。本文對各部分染色體均分別應用相同的單點交叉方法，交叉所得到的兩個子個體中，選擇其中較優的子個體進入新種群。

3.5 變異算子

為避免遺傳搜索過程過早的陷入局部最優解，算法以一定的概率進行變異。變異方法較為簡單:首先在各段染色體中均隨機選擇兩個編碼位，然后分別交換它們的位置，即可得到變異后的個體。

3.6 局部搜索過程

在每次迭代的最后，算法將應用局部搜索過程對種群中的最佳個體進行優化，以加快算法收斂速度。局部搜索過程應用2－opt 的思想，分別對各段染色體的任意兩個編碼位進行交換操作，算法將嘗試所有可能的編碼位組合，以期發現更優的個體。

4 計算實驗及分析

4.1 算法實現及參數設置

本文所提出求解軍事逆向物流網絡優化問題的遺傳算法利用C 語言在Visual C ++.net 環境中實現。算法中的參數設置如下:種群規模pop_size =30，交叉和變異概率分別設為0.8 和0.1，算法終止條件為迭代300 代。

4.2 算例及計算結果

由于沒有可用的軍事逆向物流網絡優化算例，本文自行設計了6 個算例，算例中，部隊用戶的規模分別是{50，60，70，80，90，100}，候選收集/檢測點的數量均為8 個，其開設固定成本(fi =1000)均相同，各候選收集/檢測點的安全系數si ={0.05，0.08，0.1，0.12，0.15，0.18，0.22，0.1}，維修點和報廢點的數量均分別為5 和3，各節點的位置坐標均在區間［0，100］內隨機生成，節點之間的運輸成本為相應節點之間的歐幾里得距離，各部隊用戶的返回物資量為區間［1，10］范圍內的隨機數，各收集/檢測點的能力上限各維修點的能力上限各報廢點的能力上限pdk平均報廢率r =0.2。

應用所研究的算法，對上述各算例均獨立運算10 次，得到的計算結果見表2。其中，第三列給出了10 次運算中得到的最佳解的目標函數值，第四列為10 次運算結果的平均目標函數值。

為驗證算法性能，應用所研究的遺傳算法求解了文獻［9］中的15 個有代表性的逆向物流網絡優化基準算例(算例基本情況見表3)，并將本文算法所得10 次獨立運算的平均結果與文獻［9］中模擬退火算法的優化結果進行了比較(見表4)。從表4可知，在15 個算例中，本文算法求得的13 個算例的平均結果優于文獻［9］中算法的計算結果。

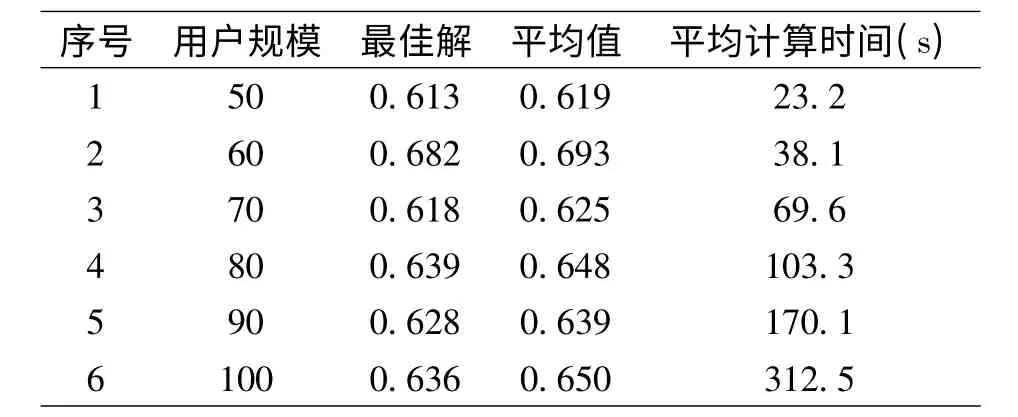
表2 計算結果

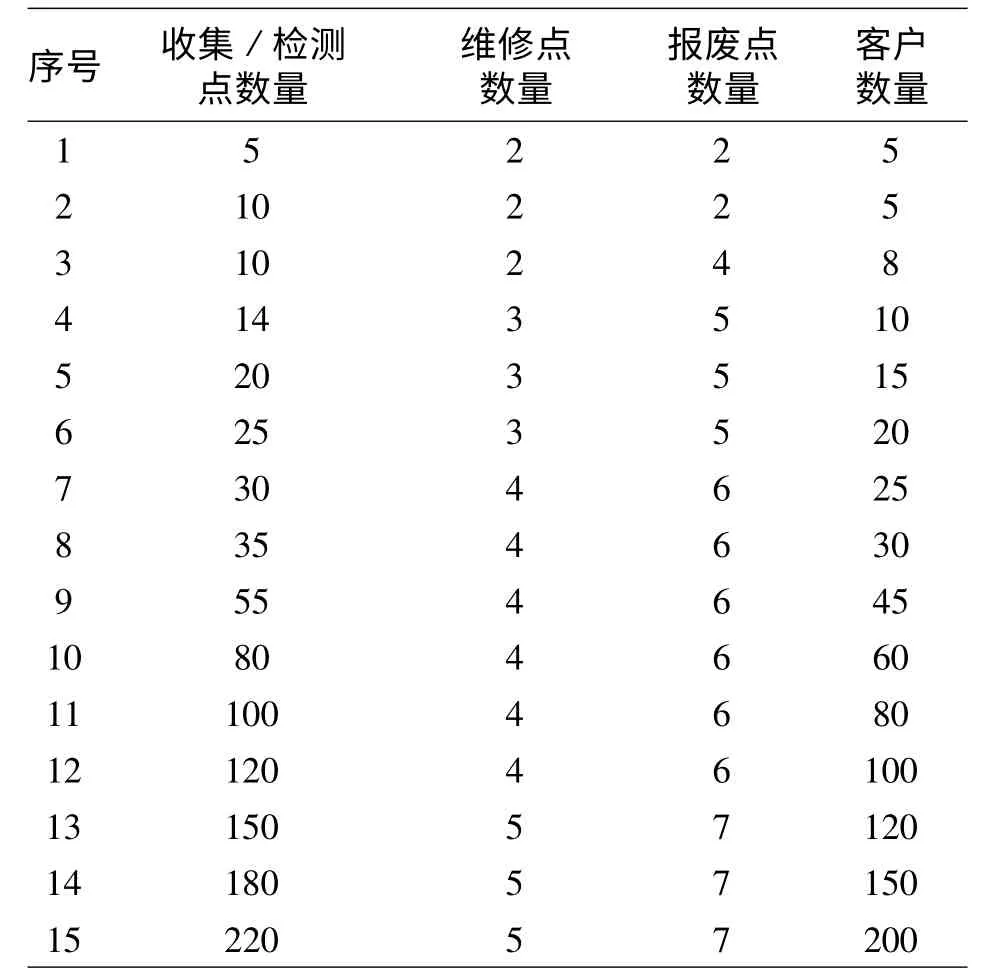
表3 基準算例基本情況［9］

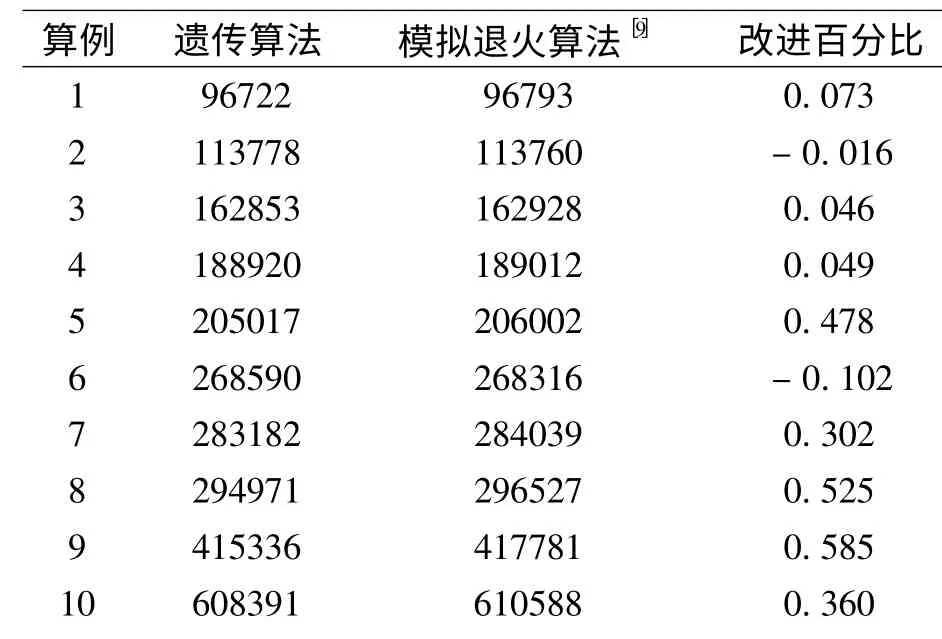
表4 本文算法與文獻［9］中算法的平均計算結果比較

11 654823 659542 0.715 12 1112097 1115163 0.275 13 1573641 1582957 0.589 14 2189368 2205633 0.737 15 3079756 3098121 0.593

5 結束語

優化的網絡結構是軍事逆向物流系統高效運行的關鍵。本文建立了軍事逆向物流網絡的優化模型，研究了求解模型的遺傳算法并完成了算法程序設計。為驗證算法性能，應用本文算法求解了文獻［9］中的基準算例，實驗結果表明:所研究的算法具有比文獻［9］中的算法更高的精度。

［1］ 毛軍凌.軍事逆向物流及其發展策略研究［D］.北京:后勤指揮學院，2007.

［2］ 姜玉宏，樊玉強，顏華.基于物聯網技術的軍事逆向物流系統研究［J］.軍隊采購與物流，2012(4):65 -67.

［3］ 張義桂，黎明.軍事逆向物流運行機制淺析［J］.軍隊采購與物流，2011(3):64 -66.

［4］ 任嵐燕，何婧.加強軍事逆向物流管理，建設資源節約型后勤［J］.軍隊采購與物流，2009(3):65 -67.

［5］ 王亞楠，司玲玲，杜海艷.基于雙向反饋信息的逆向物流網絡優化方法［J］.計算機仿真，2012，29(10):162 -164.

［6］ 高陽，劉軍.基于第三方回收再制造逆向物流網絡設計［J］.計算機系統應用，2013，22(7):16 -21.

［7］ 吳洪波，謝夢星.汽車再制造逆向物流網絡模型研究［J］. 科技與管理，2014，16(2):80 -84.

［8］ 王雁鳳，黃有方.考慮居民選擇行為的過期藥品逆向物流網絡設計［J］.華中師范大學學報(自然科學版)，2015，49(1):52 -59.

［9］ NIKNEJAD A，PETROVIC D. Optimisation of integrated reverse logistics networks with different product recovery routes［J］. European Journal of Operational Research，2014，238(1):143 -154.

［10］ ROGHANIAN E，PAZHOHESHFAR P. An optimization model for reverse logistics network under stochastic environment by using genetic algorithm［J/OL］. ［2014 -09］http://dx. doi.org/10.1016/j.jmsy.2014.02.007.

［11］ PISHVAEE MS，KIANFAR K，KARIMI B. Reverse logistics network design using simulated annealing［J］. International Journal of Advanced Manufacturing Technology，2010，47:269-281.