基于時間序列的系統盲辨識與特征提取

張銳， 黃晉英， 郎忠寶

（1.中北大學機械與動力工程學院，太原030051；2.晉西集團技術中心，太原030051）

0 引言

時間序列是利用參數模型對有序的隨機采樣數據進行處理，是一種模式識別的時域方法。采用時間序列分析方法，可以避免在振動檢測技術中因直接加窗所造成的功率泄漏，克服了求取動態數據統計特性時直接加窗造成的影響［1］。基于時間序列的齒輪箱模型理論，以其在故障診斷中損傷識別小、降噪、可操作性強等方面有明顯的優勢，在實踐和理論研究方面都有著極大潛力，因此近年來得到迅速的發展和完善［2］。

1998年，譚洪舟［3］提出一種對非高斯非最小相位ARMA模型的階p、q及相應參數的盲辨識算法，僅利用輸出信號的三階累積量來確定模型的階數和系數。并對火車車輪軸承的磨損振動信號進行建模，驗證了算法的有效性。2002年，李志農［4］研究了基于時間序列模型的盲系統辨識的參數化雙譜分析，并將此方法應用到對轉子裂紋位置、深度的確定上，通過實驗表明，參數化雙譜分析的方法是有效的，為機械故障診斷提供了一些有價值的結論。Ming Yang［5］等針對恒定負載下齒輪箱的診斷提出變化的負載和變化的速度情況下的齒輪箱故障診斷，使用ARX模型估計時域同步平均的振動數據，可以檢測齒輪損傷及局部損傷。

1 時間序列模型的建立

對于一個單輸入多輸出線性時不變系統，設其輸入為x（t），m個輸出用yi（t）表示，系統輸入到m個輸出的脈沖響應函數用hi（t）來表示，則系統模型可表示為

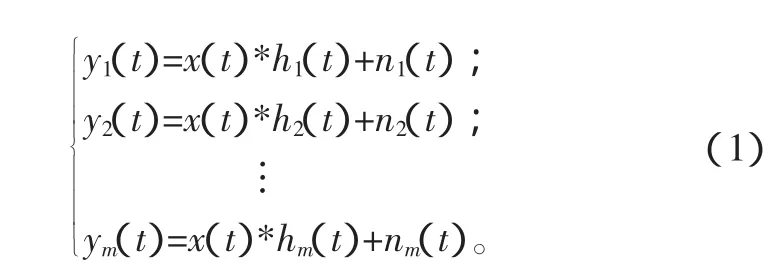
式中：*表示卷積，ni（t）為均值為零的加性噪聲。只要辨識出每個傳輸通道的hi（t），即可通過系統特性參數進行故障診斷。hi（t）可通過時間序列建模的方式獲得。

設系統輸入的采樣序列用x（n）表示，其輸出為采樣序列用y（n）表示，則其ARMA模型可表示為

式中：等式右端第一項稱為自回歸部分（AR），a（k）（k=1，2，…，p）稱為自回歸系數，p為自回歸部分的階次，代表了被辨識系統的階次；等式右端第二項稱為滑動平均部分（MA），b（k）（k=1，2，…，q）為滑動平均系數，q 為滑動平均部分的階次；ε（k）為觀測噪聲，與輸入是相互獨立的。

ARMA模型盲辨識基本的思路是利用代價函數確定ARMA模型的階次，遞推或采用某種優化算法確定其模型系數。工程上常采用FPE準則、AIC準則和BIC準則來對齒輪箱狀態模型進行定階［6］。模型的參數估計最常用的是最小二乘法、最大似然估計，高階累積量法，其中，利用高階累積量估計ARMA模型的參數具有抑制高斯噪聲的特性。首先基于三階累積量矩陣的奇異值確定AR的階數，利用累積量的切片法確定系數，在得到模型AR參數后，然后得到沖擊響應的估計h（n），再由此推出MA參數的估計值b（n），從而可以計算出模型的參數。

2 ARMA模型仿真

利用MATLAB模擬產生ARMA序列，參數設置分別為：數據點數為1024；數據維數為1；AR參數向量為［1-1.50.8］；MA 參數向量為［1］；輸入信號種類為‘exp'；噪聲方差為0.01；噪聲的概率分布類型是‘nor'。

產生的序列經過預處理后，使用上節中的方法估計模型的階數，通常采用先估計AR模型的階數再估計MA模型的階數的方式。三階累積量的奇異值、FPE準則、AIC準則、BIC準則的定階曲線如下，三階累積量的奇異值法模型階數在最大值處取得，其余三種在最小值處取得，從圖1中可看出，4種方式都可估計出階數為2。

4種方式確定的模型的AR階數為2，與真實的階數一致。分別采用基于三階累積量的殘余時間序列法、基于三階累積量的q切片法、Burg法估計模型參數。結果表明基于累積量的參數確定方法效果優于Burg法。

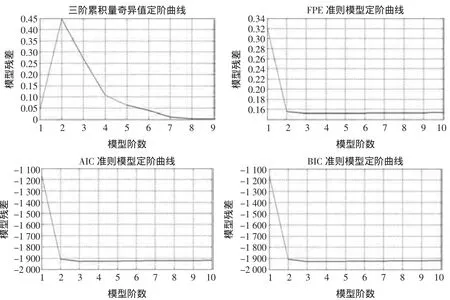
圖1 定階曲線

3 齒輪箱的ARMA模型

本次實驗在實驗室的齒輪箱故障診斷實驗臺上對某二級齒輪箱進行布點測試，并且選用LMS公司的LMS Test.Lab測試系統對齒輪箱的振動信號進行采集和簡單后處理。實驗設備包括三向加速度傳感器及LMS信號采集分析儀等。本次實驗選擇在齒輪箱的敏感振動部位布設8個傳感器，分別布置在靠近輸入軸一側的軸承座處的箱體上，測試方向為垂直向上。傳感器在箱體表面的布測編號按從左到右從上到下的順序。

建立輸入到各測點的ARMA模型，將多自由度分解成若干個單自由度系統，該系統的通用模型采用式（2）描述的模型。圖2為齒輪箱在正常工況與斷齒工況下四測點的定階曲線，根據實際計算結果和其它測點的計算情況，確定齒輪箱ARMA模型AR部分的階次為10階，MA部分的階次為1階。對齒輪箱的ARMA模型進行盲辨識，提取AR子模型的系數作為特征參量，在辨識過程中，把多輸入多輸出系統簡化成8個單輸入單輸出系統，分別辨識基于8個測點輸出信號的模型參數，表2列出了正常工況與故障工況下測點4模型的辨識結果，該模型數據的輸入軸轉速為1200 r/min。

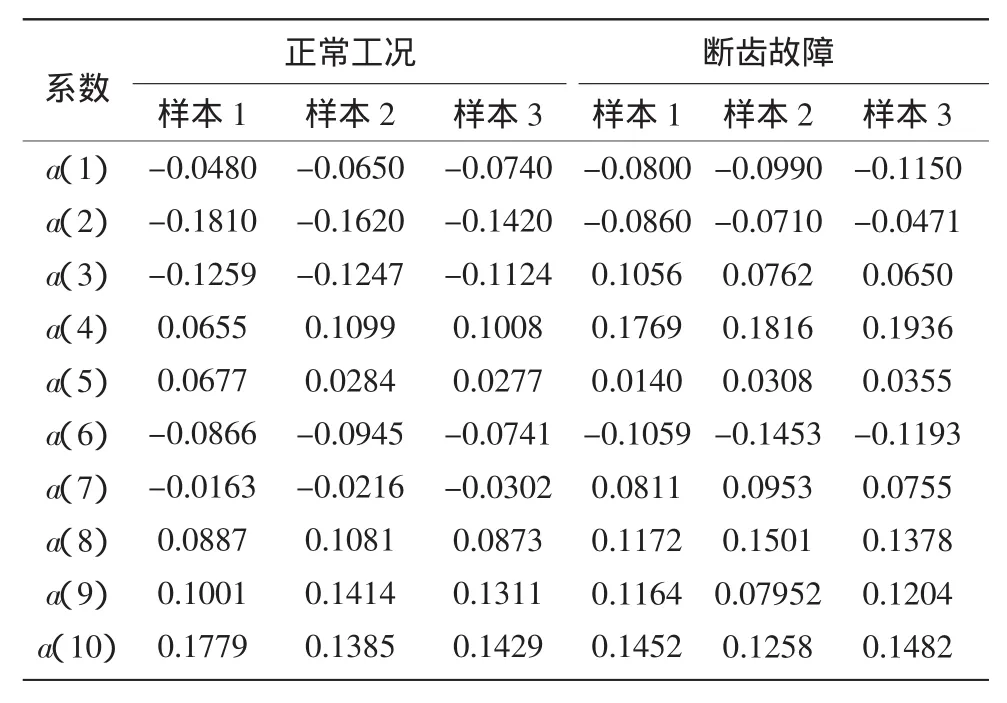
表2 AR子模型系數

盲系統辨識是僅僅根據系統的輸出來獲得特性函數的一種信號處理方法。分析了基于時間序列的盲系統辨識方法與特征提取方法，并且對ARMA模型系統盲辨識進行了仿真，仿真結果表明基于累積量的方法的有效性。齒輪箱振動信號的ARMA模型系數計算結果表明，利用時間序列所建立的系統模型的參數能較好地反映各種故障的變化，也進一步證明了結構發生故障時系統特性的變化與故障之間具有一定的對應關系。

［1］ 夏瑞花.基于時間序列分析的滾動軸承的故障診斷［D］.烏魯木齊：新疆大學，2006.

［2］ R.G.Gan An Extended FFT Algorithm for ARMA Spectral Estimation.IEEE Trans ASSP，2002，32(1)：862-870.

［3］ 黃建洪，陳致偉，傅戈雁.時間序列預測模型的建模方法與應用［J］.機械制造，2007，45（11）：1-3

［4］ 李志農.時序模型盲辨識在旋轉機械故障診斷中的應用研究［D］.杭州：浙江大學，2002.

［5］ 曹學巖.基于量子優化和ARMA模型的齒輪箱故障診斷研究［D］.太原：中北大學，2014.

［6］ 傅志方，華宏星.模態分析理論與應用［M］.上海：上海交通大學出版社，2002：25-26.