基于風電增速箱行星輪系的轉子-軸承系統模型概述
宋辰超, 王立勇, 馬超, 許寶杰, 王志
(北京信息科技大學現代測控教育部重點實驗室,北京100192)
0 引言
增速齒輪箱作為風力發電機傳動系統的核心之一,它的研究和開發是風電技術的重要內容,并正向高效、高可靠性及大功率方向發展,由于風電機組的工作環境惡劣,使得增速箱成為最容易壞的部件之一,而行星傳動系統是增速箱傳動系統中的薄弱環節[1]。因此對增速箱行星傳動系統的深入研究很有必要。
近十幾年來,各國學者對行星輪系的模型及動力學特性進行了較為深入的研究[2-4]。其中 A.Kahrama[5]建立2K-H行星傳動的扭轉模型,經固有特性分析,以解析形式給出了固有頻率的計算方法。張策、王世宇等[6]建立了2K-H行星傳動的修正扭轉模型,即在平移-扭轉模型基礎上計入了沿行星架切向的平移自由度以及行星輪軸承支撐剛度,得到了固有頻率的解析表達式。項昌樂等[7]在工程應用中,考慮時變嚙合剛度,阻尼等因素的影響,研究了針對系統的工作狀態變化對行星輪傳動非線性振動特性產生影響的分析。
上述所研究的模型分別考慮了不同的影響因素,在綜合考慮風電增速箱工況及結構之后,建立了基于風電增速箱行星輪系平移-扭轉振動模型的轉子-軸承系統模型。
1 模型的建立
根據構件運動特性的不同,行星輪模型大致可分為兩種類型:純扭轉模型和平移扭轉模型。
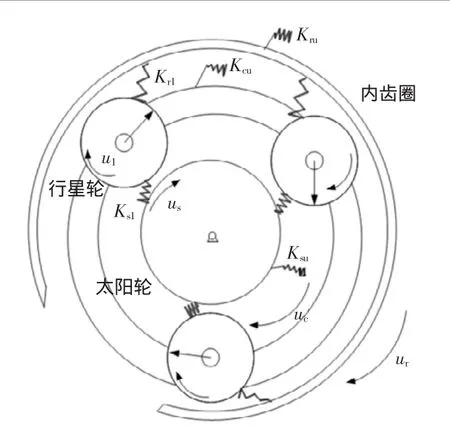
圖1 純扭轉模型
純扭轉模型是僅考慮了構件的扭轉振動的精簡模型。如圖1所示。它具有自由度少,構件內聯關系考慮少,計算量小等優點,在行星輪動態研究領域廣泛應用,由于眾多學者研究,所以建模的仿真度高,所得結果相對成熟。
行星輪除了具有扭轉自由度外,還具有沿系桿切向的平移自由度。所以國內外學者又研究了平移-扭轉模型。此外,扭轉振動模型的固有頻率與行星輪軸承支承剛度有關。因此平移-扭轉模型是考慮了行星輪軸承支承剛度和沿行星架切向平移的模型。當支承剛度與嚙合剛度之比大于10時,可以用精簡的純扭轉模型逼近復雜的平移-扭轉模型。
但是在針對實際特定情況下的行星輪,純扭轉模型顯得過于理想化,并沒有將特定情況下的有關因素考慮進去。因此依據平移-扭轉模型,計入特定因素建立了風機增速箱的行星輪模型。
為了方便建模,本文對行星輪傳動作適當簡化,并提出了以下假設:a.齒輪和軸為剛體,不考慮軸的柔性,采用集中參數模型;b.各行星輪的質量、轉動慣量,以及行星輪各個軸承支承剛度相等;c.每個構件均有3個自由度:1個繞自身旋轉的扭轉自由度和沿與軸線垂直的2個正交方向的平移自由度。
如圖2所示為直齒行星齒輪傳動系統簡圖。
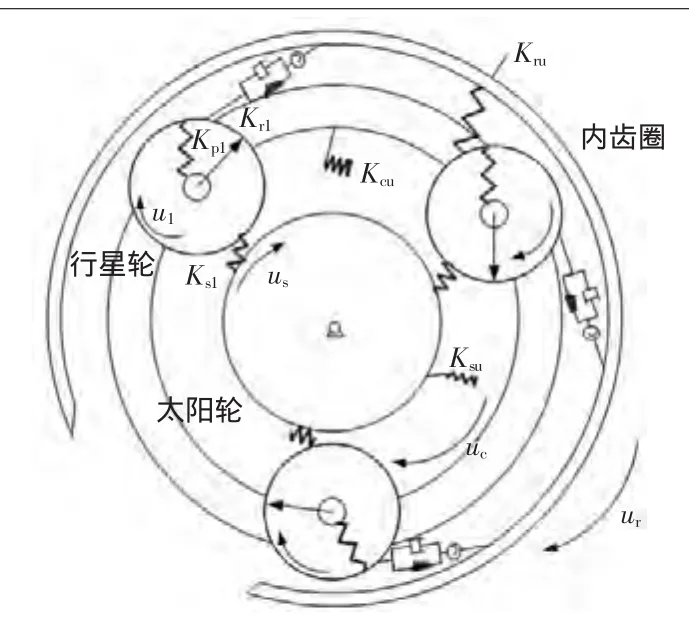
圖2 傳動計算模型
圖2 中,下標 s、c、r、n 表示太陽輪、行星架、內齒圈、行星輪。行星架的坐標系為ocxcyc。太陽輪相對于行星架的坐標系為osxsys。內齒圈相對于行星架的坐標系為orxryr。xiyi(i=1,2…n)為第i個行星輪質心的坐標。
其中 θc、θs、θr為行星架、太陽輪、內齒圈的扭轉角位移。θpi為行星輪的扭轉角位移,θbi為轉子i處的轉角。KixKiy(i=s,c,r,p)分別為太陽輪、行星架、內齒圈、行星輪的軸承剛度。KsiCsi為太陽輪與行星輪之間的時變嚙合剛度、嚙合阻尼。KriCri為內齒圈與行星輪之間的時變嚙合剛度、嚙合阻尼。KbxiKbyi(i=1,2)為軸承i處的支撐剛度。Kti(i=1,2)軸為i的扭轉剛度。erpi和espi為內齒圈與行星輪之間的嚙合誤差與太陽輪與行星輪之間的嚙合誤差。us,c,r,p為太陽輪、內齒圈、太陽架、行星輪的線位移;φi為第i個行星輪與水平方向的夾角(φi=2π(i-1)/n)。α為齒輪的壓力角。


將式帶入拉格朗日方程
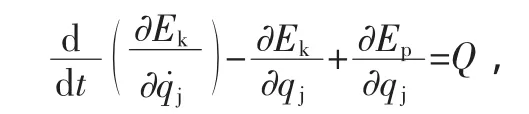
整理得矩陣方程為
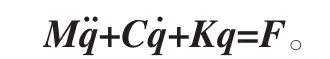
式中:q為系統的廣義自由度,q=[xcycucxryrurxsysusx1y1u1x2y2u2x3y3u3γb1γb2γ1γ2]T;
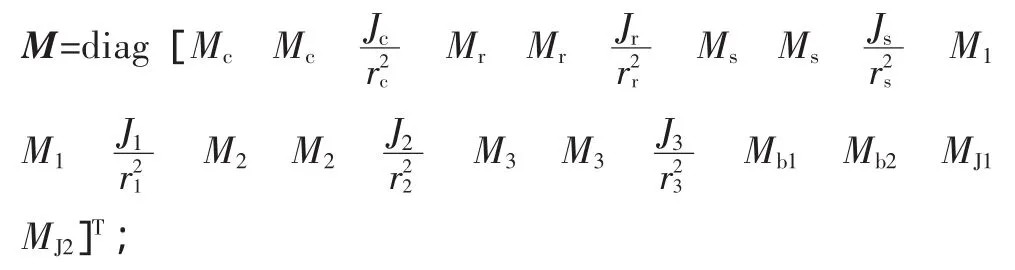



注:s表示 sin,c表示 cos。
2 系統激勵力分析
本文建模時考慮了時變嚙合剛度,綜合嚙合誤差,行星輪的安裝位置誤差,嚙合阻尼等作為內部激勵力對系統的影響。
2.1 時變嚙合剛度,嚙合阻尼
時變嚙合剛度[8]假設為周期矩形波,將其展成Fourier級數,取6次諧波項可保證足夠精度,其表達式為:
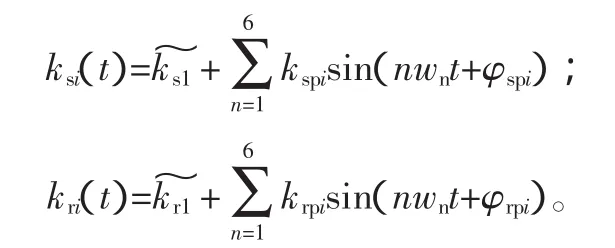
式中:ksi、kri為外、內嚙合時變剛度為外、內嚙合平均剛度;kspi、krpi為外、內時變嚙合剛度幅值;φspi、φrpi為外、內初始嚙合相位。
對于傳動系統,齒輪的嚙合阻尼對系統的內部激勵是不可忽略的,但是嚙合阻尼比較復雜,本文采用嚙合阻尼經驗公式:
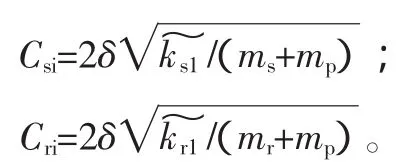
式中,δ為阻尼比,取0.07[10]。
2.2 綜合嚙合誤差
綜合嚙合誤差是由嚙合誤差、安裝誤差組成的:
espi=Essin(2πωst+φs)+Bssin(γs+α);
erpi=Ersin(2πωrt+φr)+Brsin(γr+α)。
式中:Es、Er為制造偏心誤差;Bs、Br為安裝偏心誤差;γi為外嚙合副與內嚙合副之間的嚙合相位差。
3 結論
1)純扭轉模型精煉,應用比較廣泛。但是其所考慮影響參數少,針對于特定環境的狀況適應性較差。此修正扭轉模型,不僅考慮了行星輪軸承支承剛度和沿行星架切向平移自由度,還計入了時變嚙合剛度、嚙合阻尼、綜合嚙合誤差對模型的影響。目前國內外多用此模型。
2)對于多自由度系統,若采用牛頓定律,一般都是取分離體,分別列出各分離體的運動微分方程,這就要考慮分離體之間的相互作用。本文采用能量法,從系統總體出發來列運動方程,用動能與勢能這樣的純量來描述系統的運動量與相互作用,相比于牛頓定律方法,優勢很大。
3)針對于風機齒輪箱,輸入軸與輸出軸和行星輪是一個整體。若單獨對于風機中的行星輪來建模,必然不能完全反映出此情況的特性,也會影響后續研究的準確性。因此考慮輸入輸出軸,建立行星輪系平移-扭轉振動模型的轉子-軸承系統模型。
4)此系統模型已建立,后續對于模型的動態特性的分析需要更加深入研究。
[1] 廖明夫,Gasch R,Twele J.風力發電技術[M],西安:西北工業大學出版社,2009:48-59.
[2] 孫智民,季紅林,沈允文.2K-H行星齒輪傳動非線性動力學[J].清華大學學報:自然科學版,2003,43(5):636-639.
[3] Burdess J S,Pennell J A,Rosinski J.Development of a New Three-dimensional Dynamic Model of Helical Gears[C]//Proc.Inter Gearing'94,1994:517-524.
[4] 劉瑩.風力發電機齒輪箱的齒輪轉子系統動力學的分析與研究[D],新疆:新疆農業大學,2007:32-37.
[5] Kahraman A.Natural modes of Planetary gear trains[J].Journal of Sound and Vibration,1994,173(l):125-130.
[6] 宋軼民,許偉東,張策,等.2K-H行星傳動的修正扭轉模型建立與固有特性分析[J].機械工程學報,2006,42(5):16-21.
[7] 劉輝,蔡仲昌,朱麗君,等.多工況條件下單級行星傳動非線性振動特性研究[J].兵工學報,2012,33(10):1153-1161.
[8] Abousleiman V,Velex P.A hybrid3D finite element/lumped pa-rameter model for quasi-static and dynamic analyses of planetary/epicyclic gear sets [J].Mechanism and Machine Theory,2006,41(6):725 -748.
[9] 孫智民,沈允文,王三民,等.星型齒輪傳動非線性動力學建模與動載荷研究[J].航空動力學報,2001,16(4):402 -407.
[10] 李潤方,王建軍.齒輪系統動力學-振動、沖擊、噪聲[M].北京:科學出版社,1997.

