基于時間約束的無人機避障研究

楊秀霞，劉小偉，張毅

(海軍航空工程學院控制工程系，山東煙臺264001)

0 引言

目前，無人機在軍事及民用領域已得到越來越廣泛的應用。如何使無人機能夠安全導引到目標并順利避開動態障礙物是眾多學者研究的重點課題。

最早對這一問題開始研究的是 Khatib［1］，Erdmann等［2］。后來，學者們把在靜態環境下得到成功應用的路徑規劃及避障方法推廣到動態環境中。如在文獻［3］中提到了確定及隨機的路徑地圖方法;在文獻［4］中考慮機器人及障礙物的速度，并加入到勢能函數的構造中，得到適用于動態環境的勢場法;在文獻［5］中通過動態窗口方法進行路徑規劃及避障。這些方法在靜態環境下得到了較好的結果，但是在動態環境下，尤其是應用于無人機高速運動這一特殊情況下，避障效果并不理想。其原因主要是在動態環境下，碰撞判斷及避障情況下對速度的控制與靜態環境相比，存在較大的區別。

為解決動態環境下的碰撞判斷問題，文獻［6-7］提出了基于運動學方程的碰撞判斷方法。文獻［6］定義了碰撞錐的概念，依據相對速度角度與障礙圓的切線來確定碰撞。在文獻［7］中基于視線角速度方程，對直接碰撞和間接碰撞進行了比較。

同時，考慮到動態環境下障礙物速度變化的問題，學者們提出了速度障礙的概念。例如文獻［8］在考慮運動障礙物速度的基礎上進行碰撞錐的構建，在此基礎上，通過使機器人的速度轉移到碰撞錐之外達到避障目的，但是對障礙物的速度要求必須是線性的。為解決障礙物速度為不定值的避障問題，文獻［9］通過對某一時刻，在考慮無人機及障礙物相對位置情況下，對可能的碰撞速度進行時間積分，得到非線性速度障礙集進行避障。同時考慮到多無人機之間的避碰問題，文獻［10］提出了互惠速度障礙的概念，即兩個即將相碰的無人機之間互相主動避碰，達到避碰目的。

但上面所有的方法均未考慮避障過程中避障完成時間的問題。現實情況下，只有避障完成時間小于無人機到達避障點時間，才能確保無人機成功避障。因此，基于對避障完成時間的考慮，本文提出了滑模變結構有限時間收斂制導律的避障算法，使無人機相對障礙物的速度方向在有限時間內轉移到碰撞錐之外達到避障目的。本文首先在極坐標系下建立無人機與障礙物的相對運動學方程，通過引入滑模變結構有限時間收斂制導律進行避障算法設計。最后對有限收斂時間進行分析，得到了滿足要求的參數范圍，可以使無人機的收斂時間小于到達避障點時間，確保避障完成。最后利用Matlab對設計的避障算法進行了仿真驗證。仿真結果表明，在選擇合適的參數下，無人機相對障礙物速度方向收斂到避障切線方向的時間小于無人機到達避障點的時間，驗證了算法的有效性。

1 幾何關系及運動學方程

1.1 問題描述

當無人機與障礙物在慣性空間運動時，建立無人機與障礙物的幾何關系示意圖，如圖1所示。無人機的速度大小為vuav，方向為ψuav;障礙物的速度大小為vobs，方向為ψobs。無人機相對障礙物的速度大小為vrel，方向為ψrel，其中vrel=vuav－ vobs，－ vobs為障礙物速度相反速度。由速度障礙原理，通過擴大障礙圓半徑為RP，則把無人機簡化為質點U，基于質點U及障礙圓切線BU和AU，建立碰撞區域UAB。若vrel位于UAB內，則存在碰撞危險，因此需要調整無人機的速度大小及方向，使vrel調整到UAB之外。調整時，一般考慮vrel角度變化最小即避障完成時間短、偏離原目標軌跡短原則。結合圖1，選取避障切線為BU，即避障點為B，其中避障切線BU的長度為rBU，方向為 θBU。

本文提出的避障算法是基于滑模變結構有限時間收斂制導律，使無人機能夠在有限時間內到達避障點B，且相對速度方向ψrel與切線BU方向θBU相等，確保避障完成。

圖1 無人機與障礙物幾何關系示意圖Fig.1 Schematic diagram for geometric relation of UAV and obstacle

1.2 建立運動學方程

由于假設障礙圓是剛性圓，因此B點的速度大小及航向角與圓心一致。結合圖1，在極坐標系下可得無人機U與B點之間的距離rBU及視線角θBU的變化率為:

為研究方便，建立無人機與障礙物的相對運動方程，此時無人機以相對速度vrel飛向避障點B:

式(3)給出了無人機與避障點B之間的距離變化關系，式(4)給出了無人機與避障點B之間的視線角的變化方程。

對式(4)求導，并將式(3)代入，整理可得:

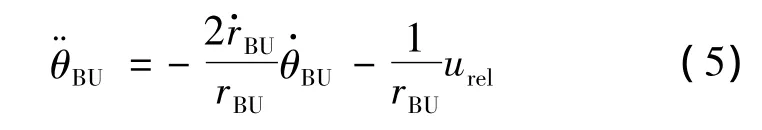
式中:urel為相對速度vrel的加速度在視線法向上的分量。

選取無人機在發現障礙物開始避障的初始時刻為t=t0，初始狀態為rBU(t0)和，初始視線角為θBU(t0)，在t時刻的狀態為rBU(t)和，令x，則式(5)可寫為:

2 滑模變結構有限時間收斂避障算法設計

無人機在避障過程中控制系統容易受到參數變化和外界環境干擾，因此制導律的設計必須考慮系統的魯棒性。滑模變結構控制對參數攝動和外界干擾具有不變性，使系統具有良好的抗干擾能力，因此基于滑模變結構控制理論設計有限時間收斂避障算法是有實際意義的。下面將基于滑模控制理論設計有限時間收斂制導律，通過選擇合適的參數，使避障完成時間小于到達避障點時間，完成避障。

2.1 制導律設計

由初始時刻x1(t0)=0，x2(t0)≠0設計非奇異滑模面為:

式中:β＞0，p和q(p＞q)為正奇數。

設計非奇異滑模控制器為:

式中:1＜p/q＜2，η＞0。

則在控制器式(10)的作用下，系統將克服外界干擾，在有限時間內到達滑模面式(9)，并且狀態量x1和x2沿滑模面運動，將在有限時間內收斂到零。

2.2 穩定性分析

對于滑模到達階段，選取Lyapunov函數:

對式(11)求導，可得:

結合式(8)和式(9)可得:

把式(10)代入式(13)得:

因此可得:

由于1＜p/q＜2，則0＜p/q－1＜1，又由于β ＞0，p和q(p＞q)為正奇數，則0時)。因此可得:

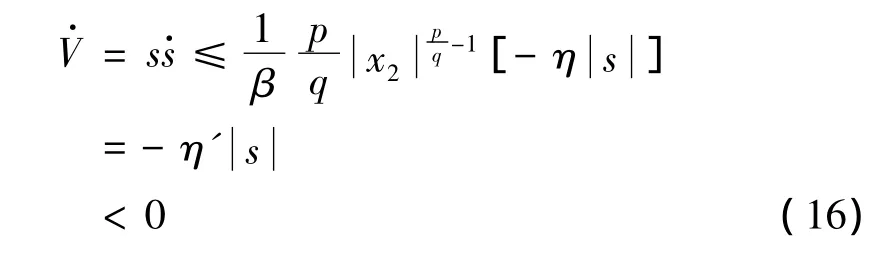
可見，控制器滿足Lyapunov穩定條件，系統狀態在有限時間內收斂到滑模面。

2.3 有限收斂時間分析

基于滑模變結構控制律，系統運動分為滑模到達和在滑模上運動到平衡點兩個階段。因此，收斂時間分為相應的兩部分。針對滑模到達階段，設s(t0)≠0到s(t)=0的時間為tr。當t=t0+tr時，s(t0+tr)=0。由得:

當 s≥0時，有:

對式(17)兩邊積分得:

則:

即:

同理，當s≤0時，有:

下一步計算狀態變量沿滑模面運動到平衡點的時間ts。考慮到系統初始條件的奇異性，設計滑模面為:

當狀態變量在滑模上運動時，滿足s=0，即:

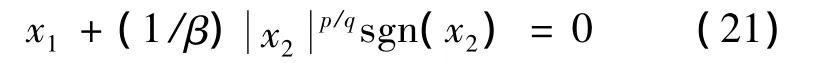
同時式(21)等價于

則:

因此總的制導系統的收斂時間可表示為:

綜上可知，所設計的制導律能夠使制導系統狀態在有限時間內收斂。由式(20)及式(23)可以看出，系統狀態到達滑模面的時間與選取的參數η成反比，即η越大，系統狀態收斂越快，收斂時間就越短;當系統狀態到達滑模面后，收斂到原點的時間與選取參數p，q及β有關。因此可以通過調節參數η，p，q及β來控制系統的收斂速度，使總的制導系統的收斂時間t小于到達避障點時間trea=rBU(t0)/vrel，完成避障。

3 無人機航向角控制

由上述避障算法設計可求出控制urel。假設相對速度大小不變，即，則由式(6)可知:

進而可知:

假設障礙物為勻速運動，則arel全部由無人機提供，因此可得無人機速度大小及方向角變化率為:

由式(27)及式(28)就可求出無人機的運動軌跡。

4 仿真結果及分析

為驗證上述避障算法的有效性，對避障算法進行仿真。

假設障礙物為勻速運動，vobs=43 m/s，ψobs=0 rad，初始坐標為 xobs0= －10 km，yobs0=10 km，無人機初始速度大小為vuav0=43 m/s，初始方向角為ψobs0=(π/2)rad，初始坐標為xuav0=0 km，yuav0=0 km，假設無人機和障礙物圓半徑RP=250 m。

通過計算，可求得無人機到達避障點B的時間為:

因此，通過選擇合適的參數η，p，q及β，可使無人機在到達避障點前相對速度角度收斂到期望角度。

通過計算，選擇η=0.002，p=8，q=7，β=0.17，仿真結果見圖2～圖7。

圖2 視線角變化示意圖Fig.2 Schematic diagram for variation of the angle of sight

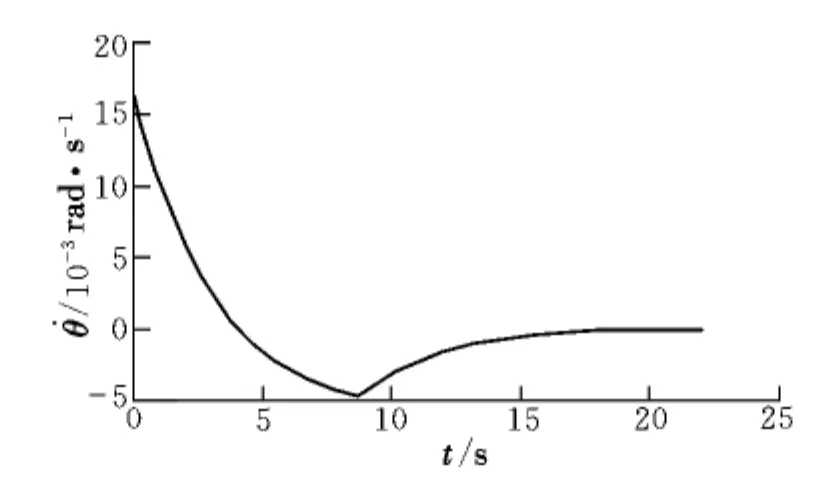
圖3 視線角速率變化示意圖Fig.3 Schematic diagram for variation of the angular rate of sight

圖4 相對速度角度變化示意圖Fig.4 Schematic diagram for variation of the angle of relative velocity

圖5 無人機速度變化示意圖Fig.5 Schematic diagram for velocity variation of UAV

圖6 無人機速度方向角變化示意圖Fig.6 Schematic diagram for variation of velocity and orientation angle

圖7 無人機避障過程示意圖Fig.7 Schematic diagram for UAV to avoid the obstacles

由圖2可知，當無人機觀察避障點B的視線角穩定時，t=20 s，小于trea=22 s，且穩定視線角與初始時刻發現避障點B的切線角相等，保證無人機能夠順利避障。由圖3可知，在t=20 s時，視線角速率，視線穩定，再次證明避障完成。由圖4可知，當t=20 s時，相對速度角度ψrel=θBU=2.717 6 rad，即相對速度角度穩定時，相對速度角度到達避障方向，避障完成。由圖5和圖6可知，無人機實際速度大小及方向角變化不劇烈，即過載不是很大，保證了過載要求。由圖7可知，障礙物圓與無人機圓相遇時兩圓相切，也就保證了避障完成。

5 結束語

本文基于無人機與障礙物之間的幾何關系，得到無人機與障礙物在極坐標系下的運動方程，在考慮避障完成時間的基礎上，通過引入滑模變結構有限時間收斂導引律，設計避障算法，選擇合適的參數，可使避障完成時間小于無人機到達障礙物的時間，保證了避障完成。仿真結果證明了該算法的有效性。

本算法的實現僅需要知道障礙物及無人機的位置及速度這4個參數，因此，算法操作起來比較方便。下一步的工作是將該算法擴展到三維空間，并對障礙物是變加速的情況進行研究。

［1］ Khatib O.Real time collision avoidance for manipulators and mobile robots［J］.The International Journal of Robotics Research，1986，5(1):90-98.

［2］ Erdmann M，Lozano-Perez T.On multiple moving objects［J］.Algorithmica，1987，2(1):477-521.

［3］ Fujimura K，Samet H.Roadmap-based motion planning in dynamic environments［J］.IEEE Trans.Robot，2005，21(5):885-897.

［4］ Ge S，Cui Y.Dynamic motion planning for mobile robots using potential field method［J］.Auton Robots，2002，13(3):207-233.

［5］ Seder M，Petrovic I.Dynamic window based approach to mobile robot motion control in the presence of moving obstacles［C］//Conf.Robot.Italy:Autom，Roma，2007:1986-1992.

［6］ Chakravarthy A，Ghose D.Obstacle avoidance in dynamic environment:a collision cone approach［J］.IEEE Transactions Systems，Man Cybernetics:Systems，Humans，1998，28(5):562-574.

［7］ Belkhouche F，Belkhouche B.Kinematics based characterization of the collision course［J］.Robot Autom，2008，23(2):127-136.

［8］ 朱齊丹，鐘訓昱，張智.基于速度變化空間的移動機器人動態避碰規劃［J］.機器人，2009，31(6):539-547.

［9］ Large F，Sckhavat S，Shiller Z，et al.Using non-linear velocity obstacles to plan motions in a dynamic environment［C］//ICARCV Control，Automation，Robot and Vision Conference.France:IEEE，2002，734-739.

［10］ Van den Berg J，Lin M，Manocha D.Reciprocal velocity obstacles for real-time multi-agent navigation［C］//ICRA Robotics and Automation Conference.CA:IEEE，2008，1928-1935.