雙時間步時域有限體積方法計算時變電磁場

雙時間步時域有限體積方法計算時變電磁場

許勇黃勇周鑄

(中國空氣動力研究與發展中心計算空氣動力研究所,四川 綿陽 621000)

摘要雙時間步被引入到時域有限體積解算器這一直接求解麥克斯韋方程組的高精度數值方法中．雙時間步方法作為非定常時間推進技巧,時間精度由物理時間步長決定,穩定性要求由定常子迭代時間步長所滿足,從而放松了通常顯式時間格式和網格對物理時間步長的限制,達到節約計算量的目的．典型目標電磁散射計算表明：通過對物理時間步長、最大子迭代步數、子迭代收斂判據的合理選取,雙時間步方法在保證計算精度的同時,能提高計算效率．

關鍵詞雙時間步;時域有限體積法;電磁散射;雷達截面

中圖分類號O441.4

文獻標志碼A

文章編號1005-0388(2015)04-0647-06

AbstractDual time stepping technique was introduced into the finite volume time domain (FVTD) method which is a high precision direct numerical solvers for time dependent electromagnetic fields controlled by Maxwell equations. As an unsteady time marching technique, the time precision is determined by physical time step, stability criterion is guaranteed by steady sub-iteration time step in this method, as a result, the physical time step was relaxed which ordinary limited by explicit time scheme and grids, the computational work is also decreased. The computation of canonical electromagnetic scattering problem demonstrated that the computational precision is conserved and efficiency is also increased; by the rational choose of physical time step, the maximum step and convergence criterion of sub-iteration in this technique.

收稿日期：2014-06-26

作者簡介

Dual time stepping FVTD method for computation of

time-dependent electromagnetic fields

XU YongHUANG YongZHOU Zhu

(ComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchand

DevelopmentCenter,MianyangSichuan621000,China)

Key words dual time stepping; finite volume time domain method; electromagnetic scattering; radar cross section

資助項目: 裝備預先研究項目(51313010303)

聯系人： 周 鑄 E-mail: stephen000@sina.com

引言

時變電磁場滿足時域麥克斯韋方程組,隨著計算機技術的發展,直接求解該方程組成為可能．與歐拉方程相同的雙曲型數學特征促進了計算流體力學(Computational Fluid Dynamics, CFD)技術在電磁場計算中的應用,其中時域有限差分(Finite-Difference Time-Domain,FDTD)法[1]和時域有限體積(Finite-Volume Time-Domain,FVTD)法[2-5]最為著名．

這些方法的時間推進或采用二階中心差分或時空耦合Lax-Wendroff格式以及多步Runge-Kutta法,其共同點是時間計算的顯式格式．以Runge-Kutta方法為代表的顯式方法,既有編程簡便,又有易實現時間高精度的優點,對時域電磁場計算是可靠的時間離散方法．但是時間顯式方法有一個最大的缺陷,其時間步長受穩定性的限制,整個計算空間必須采用統一的最小全局計算步長,為模擬幾何外形劇烈變化生成的貼體加密網格,會帶來很小的全局時間步長,從而使得到穩定的時變電磁場需要較長的計算時間,特別是在求解多維非定常問題時,計算時間的限制帶來計算量的顯著增加．另一方面,隱式計算方法雖能夠放寬計算步長的穩定性限制,但伴隨而來的是時間精度下降和矩陣求逆運算．

Jameson在CFD領域提出了雙時間步(Dual Time Stepping)隱式迭代方法[6]．該方法通過在控制方程中引入定常的虛擬時間導數項,在每個物理時間段內對物理時間導數作線性化處理,從而使得物理時間推進步長可以根據物理問題進行選取而不受穩定性的限制,計算的穩定性要求由虛擬時間子迭代滿足,子迭代的定常計算可以采用局部時間步長加速收斂．從理論上來講,引入虛擬時間迭代過程的雙時間步法,只有在子迭代殘值趨于零時才接近時間高精度,但實際計算往往難以滿足這一點,因此子迭代過程對非定常計算的影響是一個值得關注的問題．

雙時間步法在計算效率方面具有顯著的優勢,大量的CFD計算充分證實了這一點．但是雙時間步法求解時變電磁場時,需對一些因素進行必要的研究,包括物理時間迭代精度、物理時間步長、子迭代收斂標準以及最大子迭代步數的選擇,它們協同作用才能保證時間推進的效率和計算精度．本文即在已有顯式多步Runge-Kutta電磁場FVTD解算器的基礎上,拓展應用子迭代為多步Runge-Kutta的雙時間步法計算電磁散射場,極大縮短穩定電磁場所需計算時間,并計算和分析以上因素對計算結果的影響規律．

1數值方法

1.1控制方程

時域麥克斯韋方程組的兩個旋度方程(法拉第電磁感應定律和安培環路定律),在無源條件下的直角坐標系守恒形式為

(1)

式中: Q=[BxByBzDxDyDz]T=[BD]T,

B是磁感應強度矢量,D是電位移矢量; Fx=[0

-EzEy0Hz-Hy]T; Fy=[Ez0-Ex-Hz

0Hx]T; Fz=[-EyEx0Hy-Hx0]T.

對于復雜外形物體,在計算空間生成貼體多塊結構網格,其坐標變換為

k=k(x,y,z),k=ξ,η,ζ.

(2)

并得到曲線坐標系下的麥克斯韋方程組守恒型

(3)

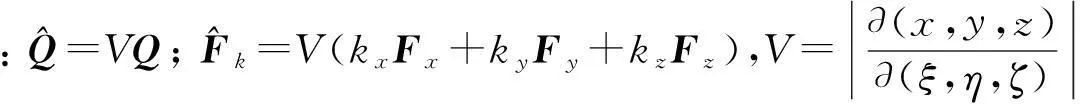
1.2空間積分方法

在計算中,守恒電磁場量在自由空間中使用散射場,可保持守恒方程形式,同式(1),從而避免在網格空間傳播入射場帶來的數值誤差,也有利于截斷空間無反射邊界條件的應用,入射電磁場可由入射波解析給出,在完全導電壁處由邊界條件引入,這也相應避免了傳統時域有限差分法中劃分總場區和散射場區的繁瑣做法．

有限體積法的空間精度體現在能否精確模擬守恒變量Q在網格單元分界面處的狀態變量,以得到相應精確的分界面通量．這里采用Steger-Warming分裂進行網格單元分界面通量計算

(4)

單元邊界左右流通量可統一寫為:

(5)

(6)

式中: S,S-為相似矩陣; Λ+,Λ-分別為正負特征值構成的對角矩陣; QL,QR分別代表分界面處左右狀態變量,它們可采用MUSCL格式而達到最高三階精度:

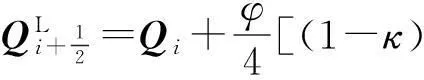
(7)

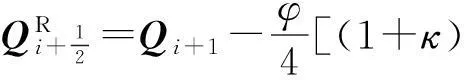
(8)

式(7)～(8)中:φ是限制器,本文中取φ=1;κ=1/3是三階精度格式的控制參數;和Δ分別是后差和前差算符．

1.3雙時間步法

對于時空分別積分的半離散線方法,顯式時間計算方面采用常微分方程求解中的Runge-Kutta法:

Qn+k/m=Qn-λαkR(Qn+(k-1)/m),k=1,m,

(9)

λ=Δt/V,

(10)

αk=1/m-k+1．

(11)

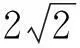
顯式方法穩定性要求全網格空間采用相同物理時間步長,會加大計算量;雙時間步方法則采用時間雙重循環,外循環為物理時間推進,內循環為虛擬時間迭代,相應雙時間步法控制方程組修改為

(12)

(13)

式中:

(14)

Q*是Qn+1(n是物理時間步)的近似,物理時間導數采用后向差分為二階時間精度．式(13)類似式(9)作顯式子迭代:

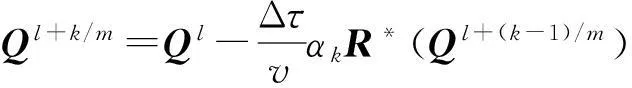
k=1,m,

(15)

上標l、l+1代表虛擬定常子迭代過程中的兩個相鄰時間層．

在數值模擬過程中,需要對內迭代收斂過程進行判斷和控制,使得內迭代過程在保證一定時間精度的前提下盡快收斂．Arnone指出[8],式(15)在物理時間步小于或與虛擬時間步同量級時變得不穩定．Melson[9]進一步明確不穩定性來源于殘差中3Q*/(2Δt)的顯式計算,物理時間步Δt越小不穩定越明顯,解決之道就是隱式化該項并作線性化處理,最后得到每層子迭代的Runge-Kutta關系為

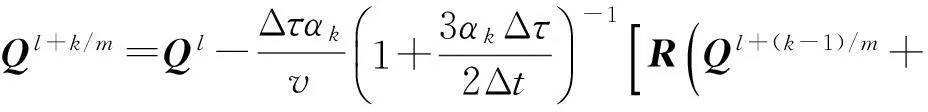
(16)

除了式(11)對應最大時間精度系數外,可以針對空間格式調節系數來增加最大時間步和改善穩定性．表1即為對應一階空間格式,步數分別為3、4、5的Runge-Kutta最大CFL數和相應系數．

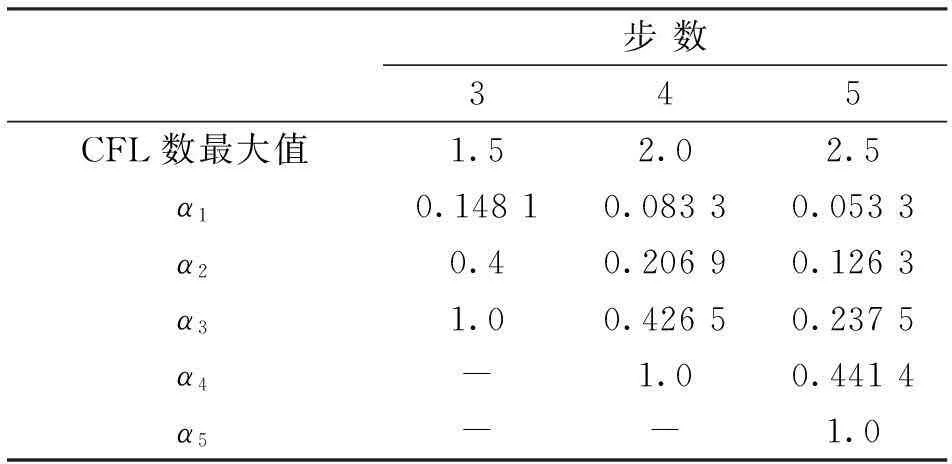
表1　多步Runge-Kutta系數和最大CFL數

由此得到簡諧波入射FVTD計算目標雷達截面(Radar Cross-Section,RCS)步驟:首先經時間推進在整個網格區域建立穩定的電磁振蕩,然后在空間Stratton-Chu積分面處逐周期進行傅里葉變換,獲得收斂的頻域電磁散射場,進而由積分方程得到目標雙站RCS分布[7]．

2計算結果與分析

雙時間步方法時間精度由物理時間步長確定,為二階時間精度;采用越小的物理時間步長時間精度就越有保證,采用較大的物理時間間隔有利于提高計算效率,但物理時間步長也不能夠無節制增加．圖1比較了不同物理時間步長對圓柱RCS結果的影響,k為波數,a為圓柱半徑,計算網格為51×46,其中物面網格選取每波長20個網格點,遠場邊界在3波長外,輻向網格壁面加密,平均約每波長15個網格點．

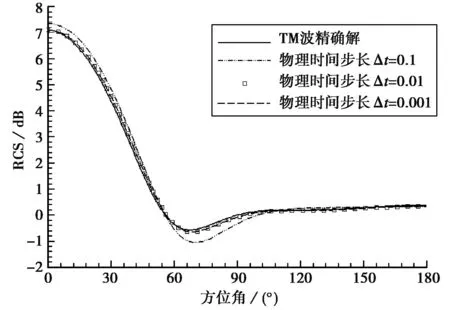
(a) TM波

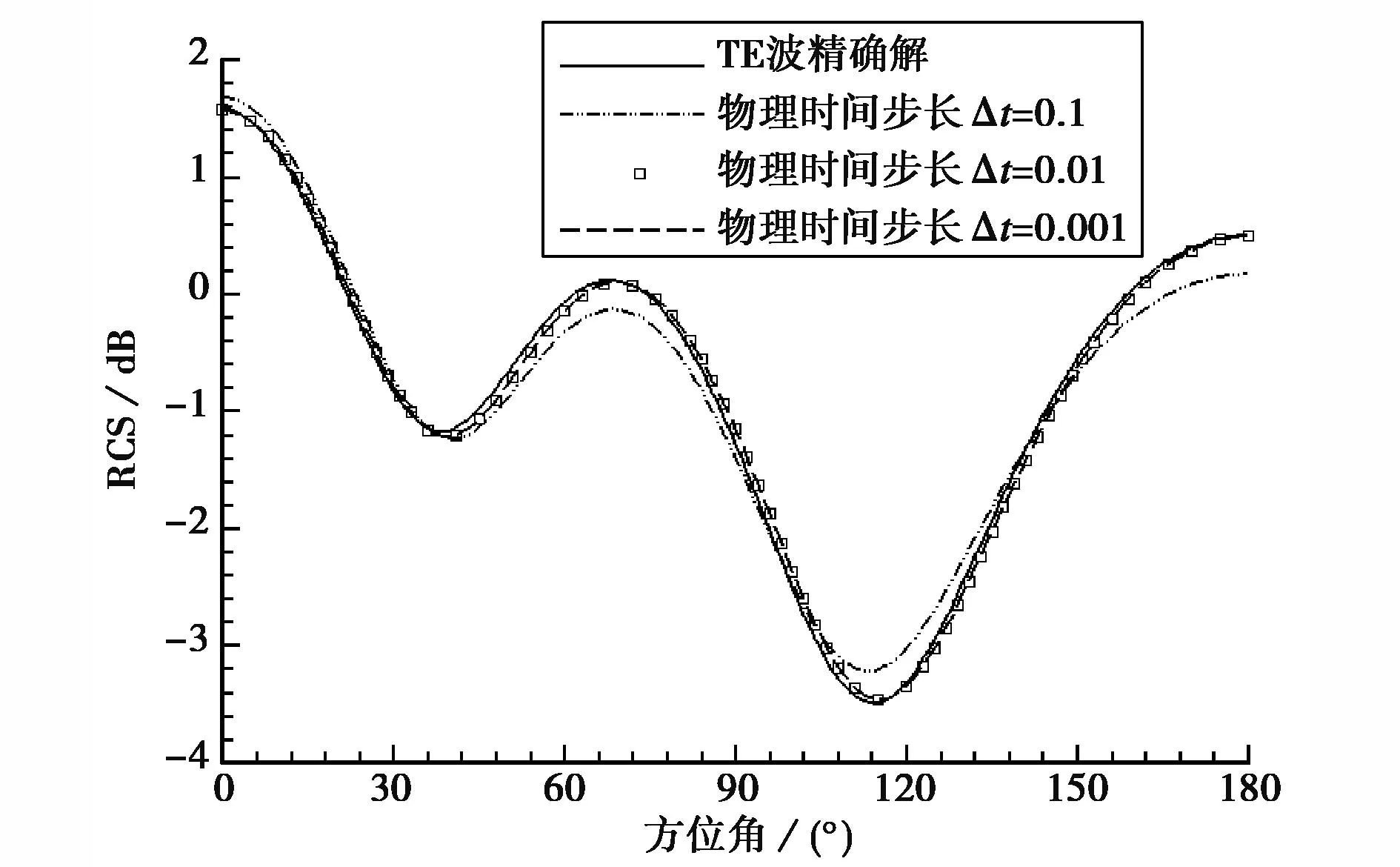
(b) TE波 圖1　物理時間步長對圓柱(ka=2)RCS的影響

物理時間步長決定了傅里葉變換中取樣周期的點數目,在保證精度前提下的更大取值有利于節約計算量,其選取與目標電尺度無關,跟電磁場空間散射特性相關,其選取由典型二維、三維計算驗證選取．由圖1知二維問題用入射電磁波周期無量綱化的物理時間步長Δt=0.01計算精度已可以,建議三維問題選擇Δt≈0.001量級,隨著物理時間間隔的增大,計算結果與參考值差別逐漸增大,在過大的物理時間步長條件下,雙時間步方法的計算精度變低．

雙時間方法非定常計算的時間精度還受到每一物理時間步上子迭代步數制約．迭代步數多,收斂控制嚴格,時間精度才有保證．真實時間步小,則子迭代可以取得少一些,數值計算中為防止場變化劇烈處、以及子迭代CFL數取得過大等情況時,殘差很有可能無法下降到收斂判據值,陷入死循環而給出最大子迭代步數,另一方面對子迭代收斂進行判斷和控制,在保證一定時間精度的前提下盡快結束迭代．本文子迭代收斂判據使用電場和磁場在計算空間最大幅度差的絕對值．

圖2是TM波入射圓柱(ka=10,網格為201×46)最大子迭代步數的影響,圖3是TE波入射圓柱(ka=10)子迭代收斂判據的影響,可見子迭代殘差下降2個量級已能滿足要求,這與CFD中殘差下降2～3個量級一致．

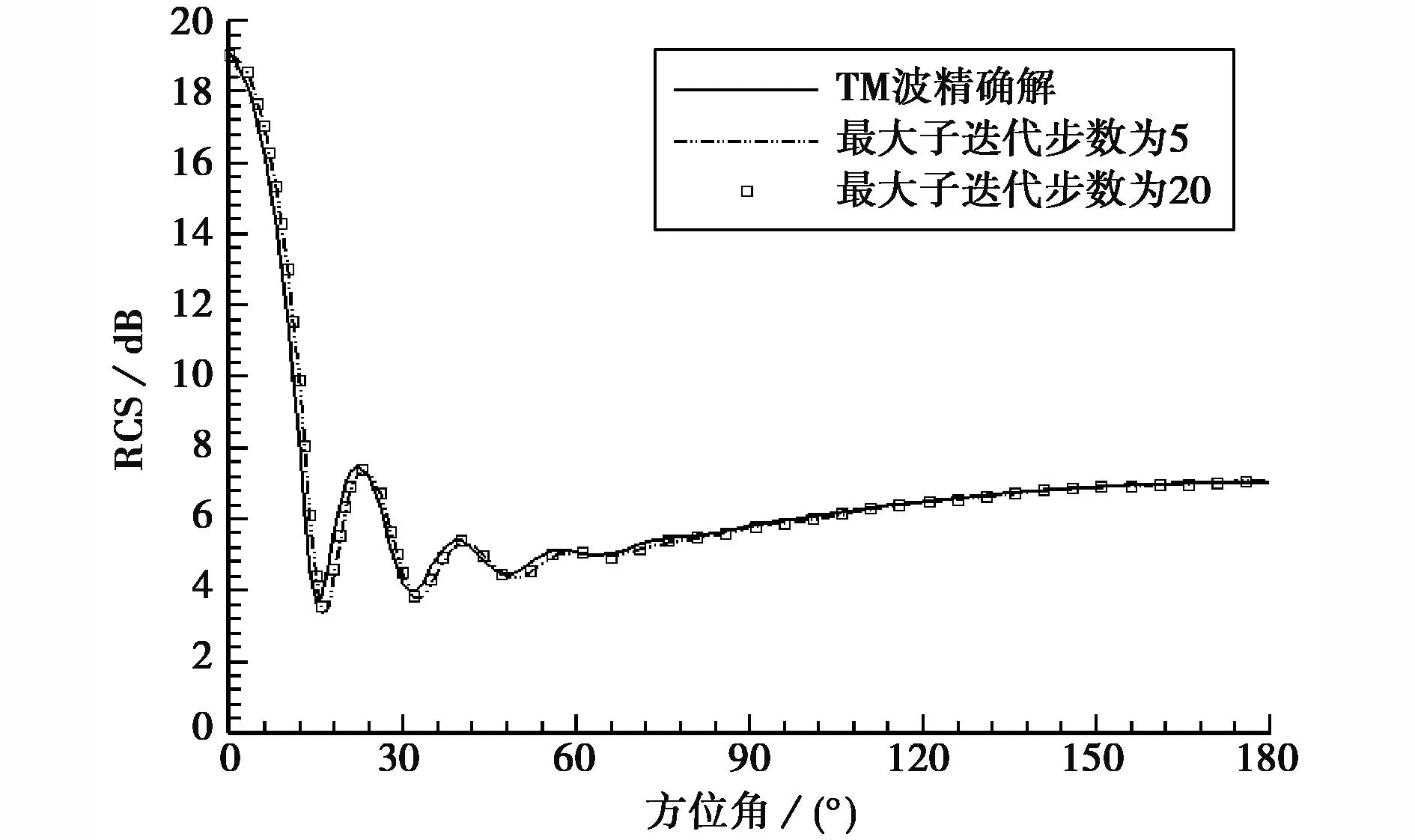
圖2　最大子迭代步數對圓柱(ka=10)RCS的影響

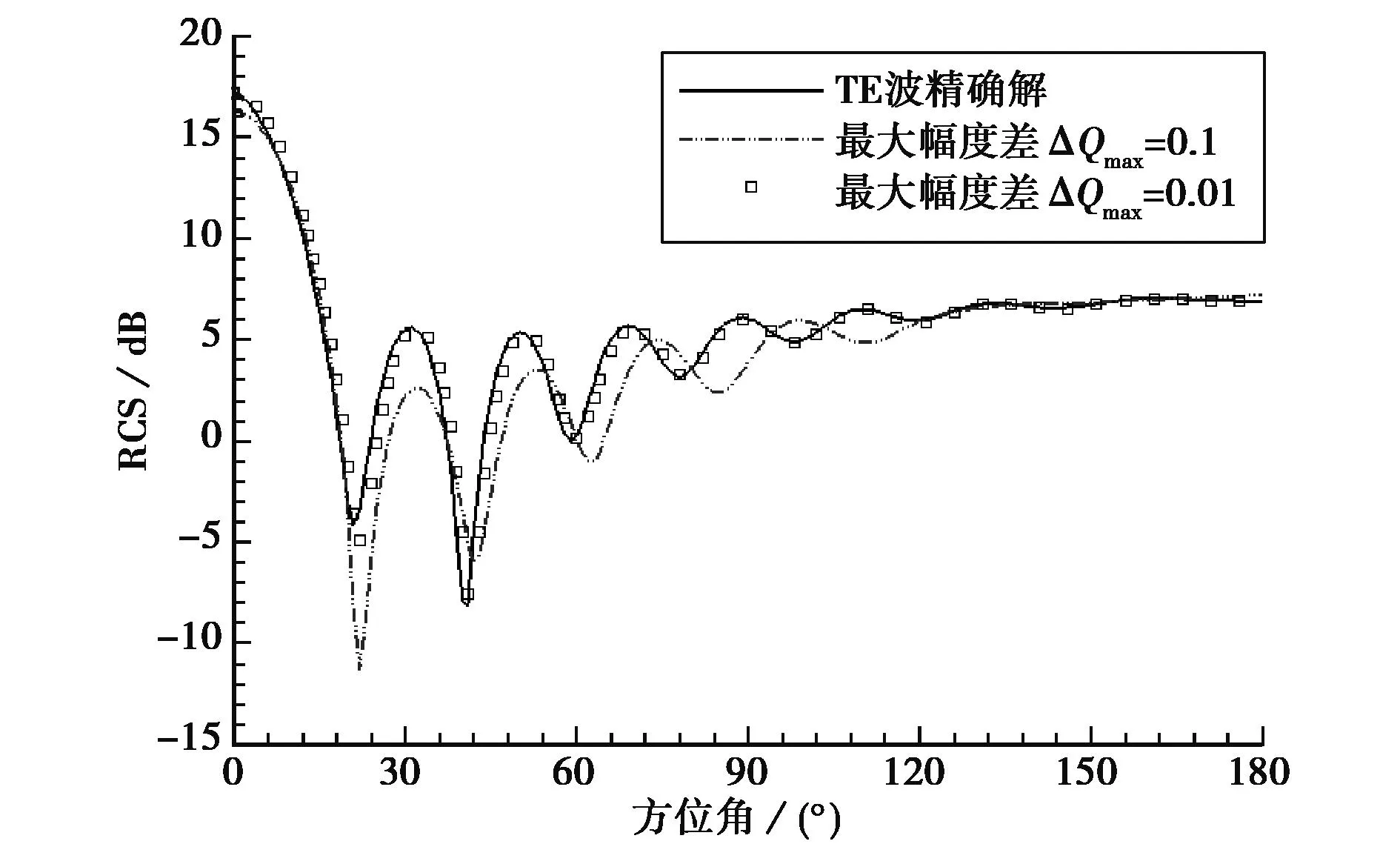
圖3　子迭代收斂判據對圓柱(ka=10)RCS的影響

以Runge-Kutta方法為代表的顯式方法容易實現時間求解的高精度,對非定常計算來說是理論上最為可靠的時間離散方法,以下針對雙時間步方法與顯式Runge-Kutta方法,就時間精度、結果好壞及計算效率作一些比較．

采用完全導電金屬球電磁散射為例,其電尺寸為ka=2,a為球半徑．計算網格為61×31×46,時間迭代都是四步Runge-Kutta推進,其他計算條件相同．圖4同一空間點分別用顯式Runge-Kutta法和雙時間步方法計算,其散射電磁場量的時間振蕩歷程、空間兩者幾無區別,說明物理時間后向差分、二階精度的雙時間方法精度滿足傅里葉變換需要．

圖5比較了顯式和雙時間步計算的RCS雙站分布,可見后者在前向(θ=180°)與解析解吻合更好．圖6則是這兩種方法逐周期進行傅里葉變換所得頻域值收斂歷程比較,在達到同樣的收斂標準(0.001),雙時間步收斂略快,這對大網格量和存在很小體積網格單元的情況,能大大提高計算效率．因為此時顯式Δt≈10-4量級甚至更小,相反雙時間步方法則根據時間精度選擇Δt,并可用局部時間步等技巧加速虛擬時間子迭代的收斂．

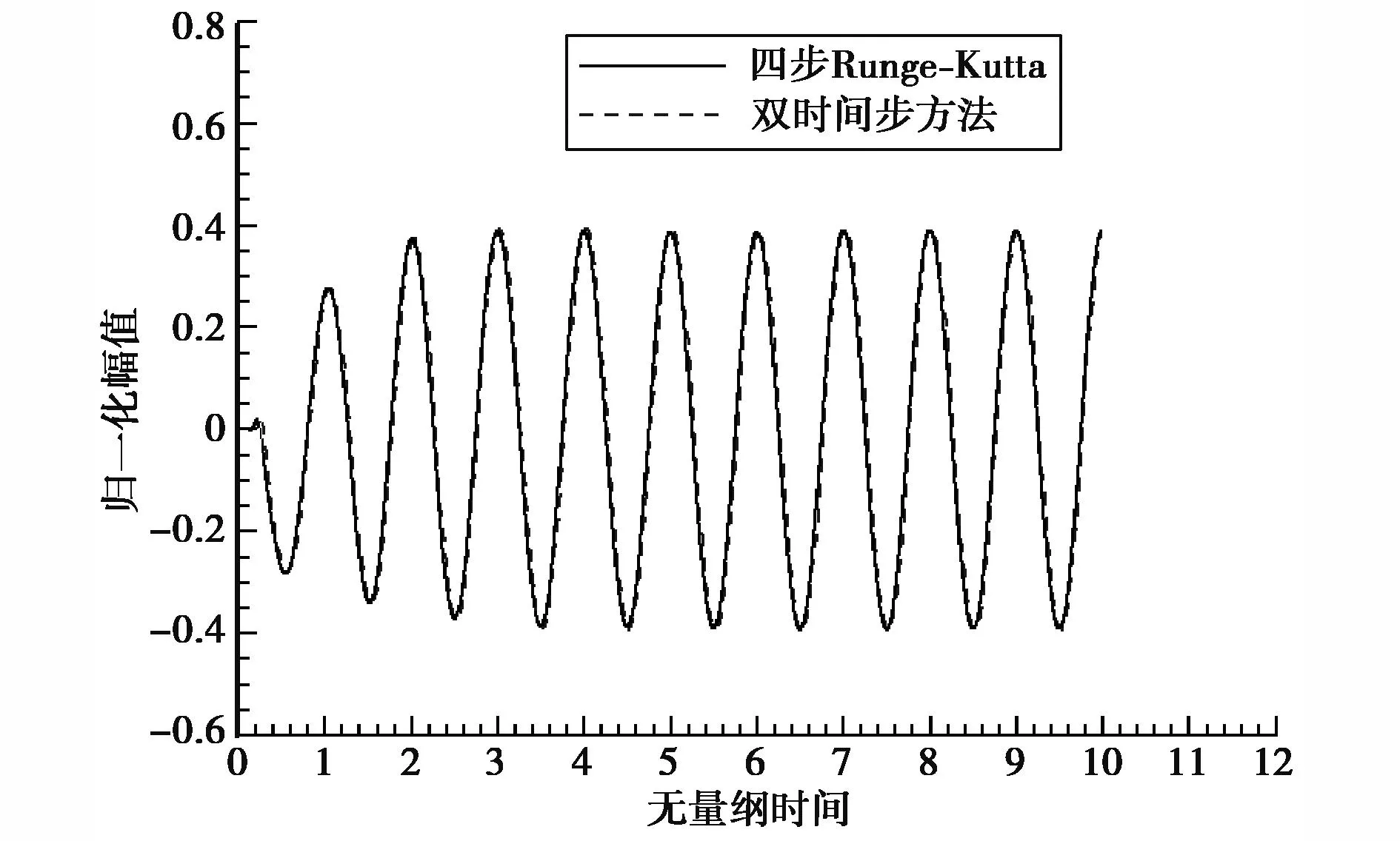
圖4　時變散射場振蕩歷程比較(金屬球,ka=2)

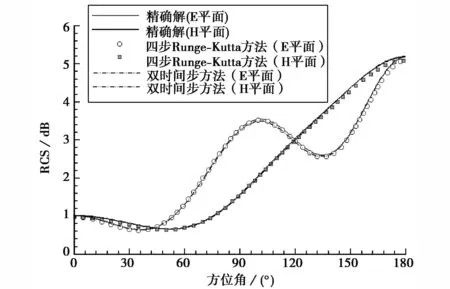
圖5　雙時間步計算金屬球雙站(RCS) 分布比較(ka=2)

圖6　電磁場頻域收斂歷程比較(金屬球,ka=2)

3結論

雙時間步時域有限體積方法計算時變電磁場,徹底放松了顯式格式穩定性對物理時間步的限制,使得時間精度由物理時間間隔決定,穩定性由定常虛擬時間子迭代(可以應用加速收斂技巧)保證,該方法可以由添加很少幾段程序由一個顯式計算程序修改而來,這樣既能保證計算精度又能大大提高計算效率的方法,值得在時域電磁場數值計算中推廣應用．

致謝:衷心感謝中國空氣動力研究與發展中心計算空氣動力研究所江雄、劉剛等人在雙時間方法應用上提供的幫助,使得該算法能在時變電磁場的計算中得到推廣．

參考文獻

[1]YEE K S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media [J]. IEEE Trans on AP, 1966, 14(5):302-307.

[2]SHANKAR V, MOHAMMADIAN A H, HALL W F. A time-domain, finite-volume treatment for the Maxwell equations [J]. Electromagnetics, 1990, 10:127-145.

[3]SHANG J S, GAITONDE D. Scattered electromagnetic field of a reentry vehicle [C]//AIAA 94-0231, 1994.

[4] 路占波, 張安, 候新宇，等. 采用FDTD/FVTD混合算法分析蝶形微帶天線[J]. 電波科學學報, 2007, 22(3): 527-532.

LU Zhanbo, ZHANG An, HOU Xinyu, et al. Analysis of bow-tie microstrip antenna by hybrid FDTD/FVTD algorithm[J]. Journal of Radio Science, 2007, 22(3): 527-532. (in Chinese)

[5]鄧聰, 尹文祿, 柴舜連, 等. 兩種適用時域有限體積法的截斷邊界[J]. 電波科學學報, 2009, 24(3): 537-540.

DENG Cong, YIN Wenlu, CHAI Shunlian, et al. Two boundary conditions for the truncation of cell-centered FVTD algorithm on unstructured lattices [J]. Chinese Journal of Radio Science, 2009, 24(3):537-540. (in Chinese)

[6]JAMESON A. Time dependent calculations using multigrid with applications to unsteady flows past airfoils and wings [C]//AIAA 91-1596, 1991.

[7]許勇, 樂嘉陵. 基于CFD的電磁散射數值模擬[J]. 空氣動力學學報, 2004, 22(2): 185-189.

XU Yong, LE Jialing. CFD based numerical simulation of electromagnetic scattering [J]. Acta Aerodynamica Sinica, 2004, 22(2):185-189. (in Chinese)

[8]ARNONE A, LIOU M S, POVINELLI L A. Multigrid time accurate integration of the navier-stokes equations [C]//AIAA 93-3361, 1993.

[9]MELSON N D, SANETRIK M D, ATKINS H L. Time-accurate Navier-Stokes calculations with multigrid acceleration [C]//Proc 6th Copper Mountain Conf. on Multigrid Methods, 1993: 423-439.

許勇(1971-)，男，四川人，中國空氣動力研究與發展中心副研究員，研究領域為計算電磁學，研究方向包括再入體電磁特性、電磁場數值計算方法.

黃勇(1970-)，男，四川人，中國空氣動力研究與發展中心研究員．研究方向為計算空氣動力學、飛行器氣動多目標優化設計．

周鑄 (1973-),男,重慶人,中國空氣動力研究與發展中心研究員.研究方向為計算空氣動力學、復雜流動分析.

胡榮旭,吳振森,張金鵬. 中國近海蒸發波導反演中最佳雷達參數分析[J]. 電波科學學報，2015,30(4):653-660. doi: 10.13443/j.cjors. 2014080501

HU Rongxu, WU Zhensen, ZHANG Jinpeng. Analysis for best radar parameter in inversion of evaporation duct above China sea areas[J]. Chinese Journal of Radio Science,2015,30(4):653-660. (in Chinese). doi: 10.13443/j.cjors. 2014080501