高精度折光修正系統射線描跡快速算法

高精度折光修正系統射線描跡快速算法

劉玉梅陳祥明趙振維孫方

(中國電波傳播研究所,山東 青島 266107)

摘要大氣折射誤差是影響外彈道測量數據的主要誤差源之一．受技術條件所限,大氣折射誤差修正在線算法常采用簡化模型,而高精度的大氣折射誤差修正往往置于事后數據處理工作中．為適應新形勢下折光修正系統數據處理的需求,基于大氣折射率隨高度的分布特征,引入“虛高”概念,并給出了高度迭代步長選取的新方法．通過與傳統方法的比較可知:改進方法在保證大氣折射誤差修正精度的同時,大大提高了射線描跡算法的運算速度;另外,該仿真結果也可為電波大氣折射誤差修正的工程應用提供參考．

關鍵詞折光修正;射線描跡;簡化模型;虛高;迭代步長

中圖分類號TN012

文獻標志碼A

文章編號1005-0388(2015)04-0749-05

AbstractThe atmospheric refraction error is a main error source among the factors affecting the flight data processing of trajectory measurement. With the restriction of technical condition, the on-line atmospheric refraction correction always uses simplified model. Usually, the high-precision atmospheric refraction correction depends on the post-data processing due to its lower real-time capability. In order to adapt the higher-precision requirements of data processing in optical wave refraction error correction system, virtual height is used and height iteration step is amended according to the distribution change of atmosphere with altitude. The comparison with the general method shows that the improved method has the same accuracy, but the speed of the ray-tracing algorithm is greatly improved. Besides, the simulation may provide valuable reference for the projects of radio wave atmospheric refraction correction.

收稿日期：2014-09-01

作者簡介

High-precision fast ray-tracing algorithm used in optical

wave refraction error correction system

LIU YumeiCHEN XiangmingZHAO ZhenweiSUN Fang

(ChinaResearchInstituteofRadiowavePropagation,QingdaoShandong266107,China)

Key wordsoptical wave refraction correction; ray-tracing; simplified model; virtual height; iteration step

資助項目: 國家自然科學基金(No. 41305024，No. 41205024)

聯系人： 陳祥明 E-mail：xmch22s@163.com

引言

大氣折射效應會引起光波傳播時延和路徑彎曲,導致探測與定位誤差,是影響外彈道測量數據的主要誤差源之一．過去受計算機硬件條件的限制,在實時性要求較高的大氣折射誤差修正工程應用中往往采用簡化模型[1-4],盡管滿足了實時修正的要求,卻犧牲了大氣折射誤差的修正精度,尤其對于大氣結構復雜多變的情況;另外,簡化模型大都是基于統計結果得到經驗模型,精度相對較高的簡化模型往往加入了實測地面氣象數據[5],也只能反映在此種氣象條件下的大氣的平均折射效應,常用于無法獲取高空大氣結構的情況．

隨著雷達測控領域的發展,簡化模型已滿足不了高精度外彈道測量實時數據處理工程應用中對精度的需求．同時,隨著硬件技術的革新,計算機本身的運算速度也有了長足的進步,使得高精度快速修正成為可能．

利用射線描跡算法仿真計算了由于大氣折射引起的測距和測角誤差,重點討論了已知測站上空大氣剖面條件下,提高大氣折射誤差計算速度的有效途徑,通過與傳統方法的比較驗證了改進方法的實用性;本文的方法也可直接應用于工作頻率較高(如X頻段以上)的無線電測量系統的大氣折射誤差修正,也可為只考慮對流層(在折射修正工程應用中,對流層往往指地面至60 km左右高度的整個中性大氣層[1])大氣折射效應的工程應用提供參考．

1射線描跡法

射線描跡法假定大氣球面分層,基于Fermat最小光程原理和Snell定律這兩個幾何光學原理給出的,計算精度高,在實際中得到廣泛應用[6]．大氣層中光波的傳播軌跡示意圖見圖1.

圖中,a為地球半徑,h0和hT分別為測站和目標的海拔高度,θ0和α0分別為測站測得目標的視在距離和測站到目標的真實仰角,R0為測站到目標的真實距離,Rg為光波實際傳播路徑．

1.1距離誤差

1)目標視在距離

目標視在距離Re是測量設備測得的目標距離,與視在仰角θ0和傳播路徑上的大氣折射指數n分布有關:

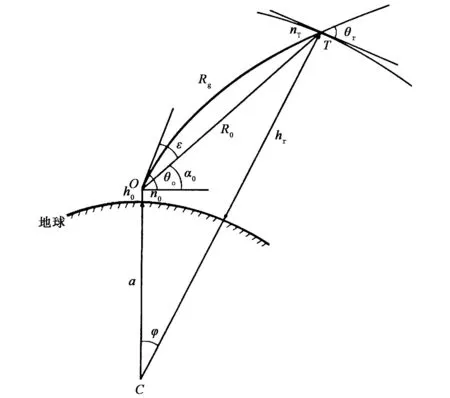
圖1　大氣中光波傳播軌跡示意圖

(1)

式中: r為地心距,r=a+h;由Snell定律知:nrcosθ=const; 記A0=n0r0cosθ0,則:

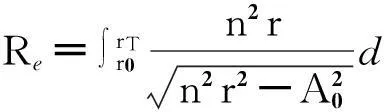
(2)

2)目標真實距離

在△COT中,根據余弦定理得:

(3)

根據式(1)～(3),得到大氣折射引起的距離誤差,記為ΔR,則:

ΔR=Re-R0.

(4)

1.2仰角誤差

1)測站與目標間地心張角

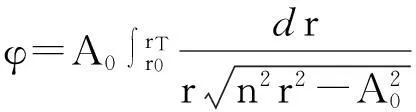
(5)

2)目標真實仰角

在△COT中,根據正弦定理得

(6)

記大氣折射引起的仰角誤差為ε,則:

ε=θ0-α0.

(7)

從式(1)～(7)可知:計算光波大氣折射引起的測距和測角誤差,需要已知傳播路徑上大氣折射指數剖面和目標的真實高度．對于前者,國內外學者給出了多種獲取大氣折射指數剖面的方法[5,7],不予贅述;對于后者,工程上常基于測得目標的視在距離Re和視在仰角θ0,通過迭代的方法逼近得到．

2傳統方法

2.1目標真實高度

文獻[8]中給出了已知大氣折射率剖面,基于目標的視在距離Re和視在仰角θ0用迭代法逼近目標真實高度hT的方法,也是目前工程中通用的方法,算法流程為:

1) 取天線高度h0為迭代初值,即:hT=h0;

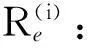
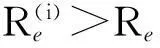
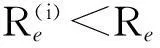
2.2對流層高度以上處理

對折光修正系統而言,對流層高度以上空域的大氣折射效應可以忽略,即在此空域可以認為光波沿直線傳播．文獻[1]和文獻[9]給出了計算這一空域大氣折射誤差的有效簡易方法,基于三角形幾何關系計算距離和地心張角,替代運算較復雜的數值積分．具體為:

1) 目標視在距離

(8)

式中： H為對流層高度,常取60km； Re(H)為測站至H高度處的視在距離．

2) 目標與測站地心張角

(9)

式中,φ(H)為測站與H高度處的地心張角．

3改進方法

3.1目標初始高度

不難看出:傳統方法計算目標的真實高度算法中,迭代初始高度取天線高度,造成步驟3)中多次重復步驟2),勢必增加運算時間,對于高空目標尤為明顯．

“虛高”是電離層垂測數據(頻高圖)判讀中常用到的術語[10],在數值上等于真空傳播假設條件下對應的目標高度．大氣球面分層假設下,虛高hv的計算公式為

(10)

顯然,目標的虛高大于其真實高度．

3.2高度迭代步長

式(1)兩邊對r求導數,得:

(11)

由于對流層大氣折射指數n隨高度的增加而遞減[5,7];結合式(11),不難得出:在視在仰角θ0一定時,視在距離的變化梯度隨高度增加是遞減的;換言之,如果按視在距離的變化量等比例選取高度步長,計算得到的視在距離大于其真實值．基于此,對迭代算法進行改進,算法流程為:

1) 計算目標的虛高hv,并作為目標高度的迭代初值,即:hT=hv;

4對比與分析

統計表明:大氣折射引起的天頂延遲在2.3 m左右,即使在1°時高度誤差也只有20 m左右[1,10],這使得引入“虛高”,很顯然會大大減少步驟3)的運算時間;在此不針對這一點與傳統方法進行比較,重點比較步驟4)對算法的改進效果．

作為試算個例,統一取目標的視在距離Re=300 km,取eps=0.01 m,大氣折射率剖面由參考標準大氣[11]換算得到,剖面高度步長取1 km;數值積分算法采用龍貝格(Romberg)數值積分算法[12]．

圖2給出的是視在仰角θ0在1°～90°范圍內傳統方法與改進方法迭代次數的對比結果．

從圖2可以看出:傳統方法的迭代次數都在10次以上,而改進方法的迭代次數都在5次以下,在視在仰角大于40°時，1次迭代即可，改進方法大大減少了運算迭代次數.

圖3給出是高度迭代步長取剖面步長,其它條件不變的條件下,視在仰角θ0在1°～90°范圍內用改進方法完成一組誤差值計算的耗時曲線(計算機配置:E8400酷睿雙核CPU、2G內存)．

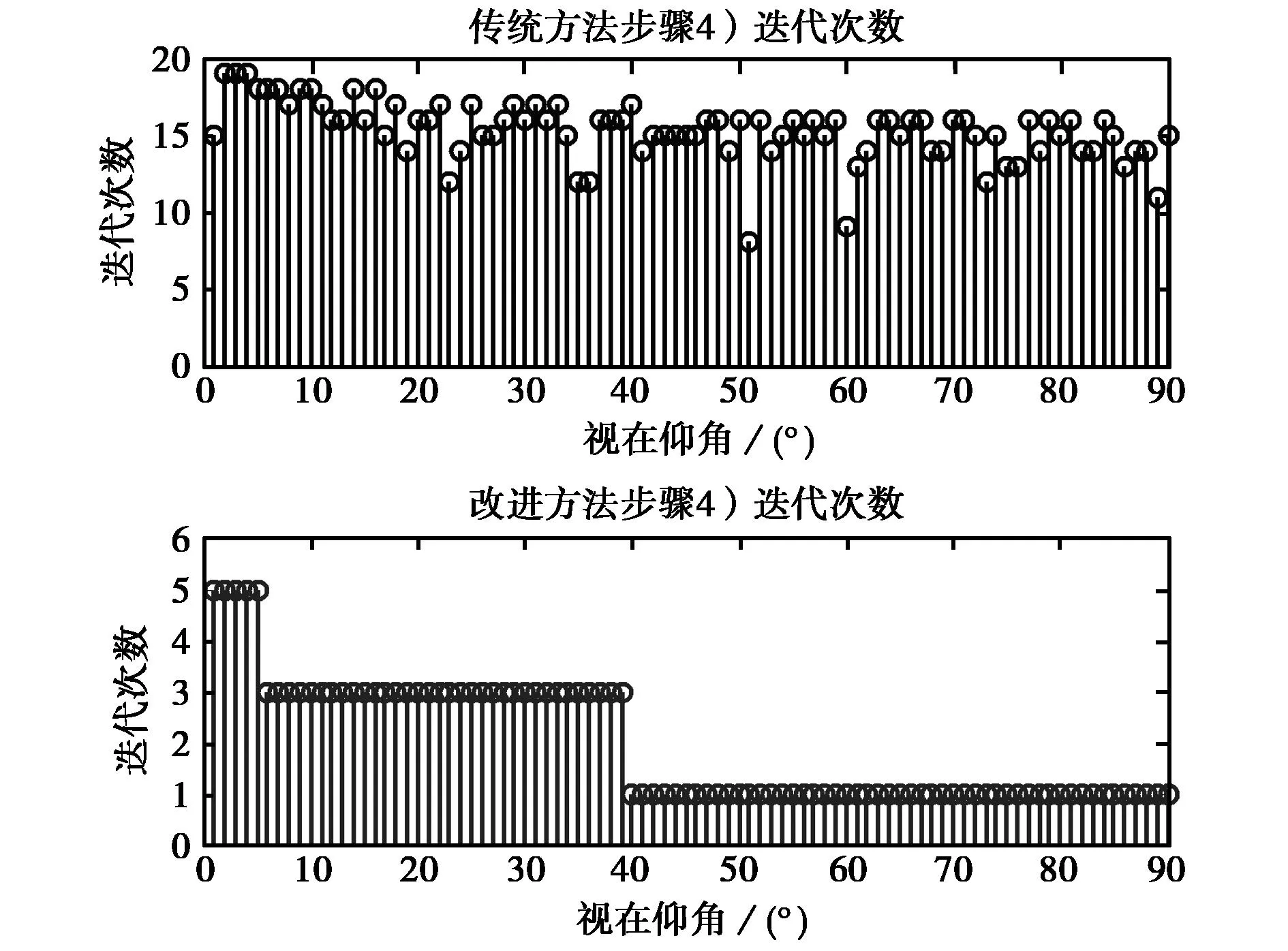
圖2　不同視在仰角時兩種方法的 迭代次數比較

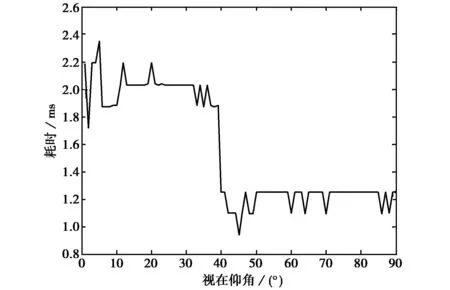
圖3　改進方法完成一組誤差值的計算耗時 隨視在仰角變化曲線

目前,測控系統采樣間隔多為1 s,在此計算機配置條件下,改進方法完成一組誤差值計算的耗時在3 ms以下,完全可以滿足該前提條件下的近實時修正需求．

同時,算法中高度迭代步長的選取也會影響計算時間．圖4給出的是視在仰角為5°,高度迭代步長取0.01～1 km時改進方法完成一組誤差值計算的耗時仿真結果．

從圖4可以很明顯看出:高度迭代步長越大,完成一組誤差值計算耗時越少,主要是由于高度迭代步長越大,步驟3)的耗時越少;如果高度迭代步長足夠大,甚至直接由步驟2)進入步驟4)．

筆者仿真了不同的目標視在距離(包括:Re<300 km和Re>300 km的情況),以及更高精度需求(eps?0.01 m)時,在既有計算機配置條件下,改進方法較傳統方法的運算速度都有顯著的提高,在此不一一列出．

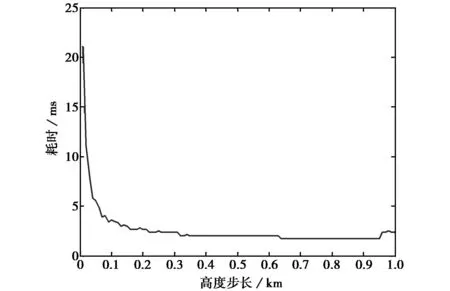
圖4　不同高度迭代步長完成一組誤差值計算耗時

5結論與討論

基于對流層大氣折射率隨高度的分布特征,引入“虛高”概念,并改進了高度迭代步長選取方法,通過比較得知:改進方法在保證精度的同時,大大縮短了誤差計算時間,說明針對折光修正系統射線描跡算法的改進是有效的,具有較強的實用價值．需要說明的是:

圖3是基于既有計算機配置、剖面高度步長取1 km時的仿真計算結果,配置不同、剖面步長取值不同(見圖4),仿真結果會有所不同．

精度需求也會影響計算速度,本文選取的測距精度在0.01 m,對應的距離誤差精度遠在0.01 m以上,實際工程應用中定位精度需求不見得如此之高．

數值積分算法的選取也是影響計算速度的一個因素,其影響程度需要結合剖面步長綜合考慮,不是本文重點,不予詳細展開．

本文的改進方法不限于應用于折光修正系統．眾所周知:對于無線電測量設備而言,如果設備的工作頻率足夠高,電離層大氣引起的折射效應往往可以忽略[13-14],此時電波大氣折射誤差的計算可以等同于光波大氣折射誤差的計算．由此,本文改進方法可以直接用于高頻無線電測量系統的大氣折射誤差修正;同時,本文改進方法也可為只考慮對流層大氣折射效應的無線電測量系統提供參考．

參考文獻

[1] 黃捷, 張仁芳, 胡大璋. 電波大氣折射誤差修正[M]. 北京: 國防工業出版社, 1999: 133-137.

[2] 謝益溪, 拉菲涅特J, 蒙J P, 等. 電波傳播——超短波·微波·毫米波[M]. 北京:電子工業出版社, 1990: 67-82.

[3] 吳希德, 張武良, 韓文俊. 對流層距離誤差預報法的檢驗與改進[J]. 電波科學學報, 1994, 9(2): 71-77.

WU Xide, ZHANG Wuliang, HAN Wenjun. Test and improvement of prediction method for tropospheric range error[J]. Chinese Journal of Radio Science, 1994, 9(2): 71-77.(in Chinese)

[4] 韓文俊, 趙紅梅. 預報對流層大氣折射誤差的新公式[J]. 電波科學學報, 2005, 20 (4): 458-461.

HAN Wenjun, ZHAO Hongmei. A new formulate for predicting tropospheric refractive error[J]. Chinese Journal of Radio Science, 2005,20(4):458-461. (in Chinese)

[5] 陳祥明. 大氣折射率剖面模型與電波折射誤差修正方法研究[D]. 青島: 中國海洋大學, 2008.

CHEN Xiangming. Studies on Atmospheric Refractivity Profile Model and Radio Wave Refractive Error Correction Method[D]. Qingdao: Ocean University of China, 2008. (in Chinese)

[6] 楊志強, 陳祥明, 趙振維. 對流層電波折射誤差修正經驗模型研究[J]. 電波科學學報, 2008, 23(3): 580-584.

YANG Zhiqiang, CHEN Xiangming, ZHAO Zhenwei. Empirical model for radio wave refractive error correction of troposphere[J]. Chinese Journal of Radio Science, 2008, 23(3): 580-584.(in Chinese)

[7] BEAN B R, DUTTON E J. Radio Meteorology[M]. New York: Dover Publications Inc, 1968: 49-89.

[8] 劉利生. 外測數據事后處理[M]. 北京: 國防工業出版社, 2000: 248-250.

[9] 祝轉民, 李恒年, 黃永宣, 等. 電波折射誤差修正的精確模型與在線算法[J]. 系統工程與電子技術, 2003, 25(3): 287-289.

ZHU Zhuanmin, LI Hengnian, HUANG Yongxuan, et al. An exact model and on-line algorithm for radio refraction error correction[J]. Systems Engineering and Electronics, 2003, 25(3): 287-289. (in Chinese)

[10]焦培南, 張忠治. 雷達環境與電波傳播特性[M]. 北京:電子工業出版社, 2007: 252-261.

[11]ITU. ITU-R P.835-5 Reference Standard Atmospheres[S]. Geneva: International Telecommunication Union, 2012.

[12]徐士良. C常用算法程序集[M]. 北京: 清華大學出版社, 1996: 143-145.

[13]ITU. ITU-R P.531-11 Ionospheric Propagation Data and Prediction Methods Required for the Design of Satellite Services and Systems[S]. Geneva: International Telecommunication Union, 2012.

[14]李建儒, 劉玉梅, 趙振維, 等. 衛星測控電波折射修正效果分析[C]//2007年航天測控技術研討會論文集. 北京, 2007: 135-138.

劉玉梅(1978-),女,山東人,中國電波傳播研究所高級工程師,碩士,主要從事電波傳播、數據庫及軟件系統研發等方面的工作．

陳祥明(1983-),男,山東人,中國電波傳播研究所工程師,碩士,主要從事大氣環境建模及折射修正方面的工作．

趙振維(1965-),男,河北人,研究員,博士,中國電波傳播研究所總工程師,中國電子科技集團公司首席專家,享受國務院政府特殊津貼,現為中國電子學會高級會員、中國宇航學會飛行器測控委員會委員,長期從事電波環境及其傳播特性方面的工作．

孫方(1982-),女,山東人,2004年畢業于西安電子科技大學通信工程學院,現在中國電波傳播研究所青島研發中心從事電波傳播、大氣波導等方面的工作．

葛行軍, 張軍, 靳振興, 等. 雙諧振腔長脈沖相對論返波振蕩器研究[J]. 電波科學學報,2015,30(4):754-758. doi: 10.13443/j.cjors. 2014090801

GE Xingjun, ZHANG Jun, JIN Zhenxing, et al. Investigation of a aong-pulse relativistic backward wave oscillator with dual resonant cavities [J]. Chinese Journal of Radio Science,2015,30(4):754-758. (in Chinese). doi: 10.13443/j.cjors. 2014090801