基于自抗擾控制技術的無人機編隊控制器設計

李一波，胡楊，陳偉，王毅

(1.沈陽航空航天大學 自動化學院，遼寧 沈陽110136;2.中航工業成都飛機工業(集團)有限責任公司 技術中心，四川 成都610000)

0 引言

無人機編隊飛行［1］是指兩架或者多架無人機(UAV)為適應任務要求，以一定結構的某種隊形排列飛行。與單架無人機相比，無人機編隊可以顯著提高完成作戰任務的效率［2］。編隊飛行主要包括隊形設計、飛行過程中的隊形保持，也包括根據外部情況以任務需要進行的隊形動態調整變換。

無人機編隊控制問題的研究主要集中在編隊隊形保持控制方面，國內外許多研究機構針對上述問題進行了廣泛的研究。文獻［3-4］采用了經典PID控制方法進行控制系統設計。文獻［5］應用自抗擾控制策略設計了姿態角跟蹤回路，驗證了自抗擾控制器具有很強的魯棒性。文獻［6］考慮到編隊時的氣動耦合和外部干擾，設計了神經網絡自適應逆控制器。文獻［7］提出了一種利用高階滑模控制的思想設計編隊飛行保持控制器。以上文獻提出的思想雖然解決了編隊隊形保持的問題，但在現實編隊飛行過程中，系統容易受到外界干擾和航向測量誤差等各種因素的影響，從而導致控制器的性能大大降低，難以滿足實際應用時對編隊指令控制精度和響應速度等方面的要求。

自抗擾控制(ADRC)技術最先是由我國韓京清研究員提出的一種非線性控制策略［8］。它一方面發揚了經典PID控制方法的不依賴于模型的精準性，僅基于誤差反饋進行控制的優點;另一方面又結合了現代控制理論的成果，通過建立擴張狀態觀測器(ESO)對外界和內部的擾動進行實時估計和補償，從而避免了積分作用的缺陷。本文基于長機-僚機結構，設計了自抗擾控制器，通過編隊指令的輸入可以完成編隊過程的保持和變換。仿真結果表明，該控制方法控制精度高、超調量小、抗干擾性強，性能遠優于現有的PID控制方法。

1 編隊飛行相對運動數學模型的建立

以其中一架UAV和有人機斜線編隊為例進行分析。采用固連于僚機的旋轉參考坐標系(見圖1)，其x軸方向與無人機的速度矢量方向一致。

圖1 編隊飛行幾何關系圖Fig.1 Formation flight geometric relationship

因在同一高度下的水平面內，在不考慮高度方向的情況下，長機與其編隊內的UAV的相對運動方程為:

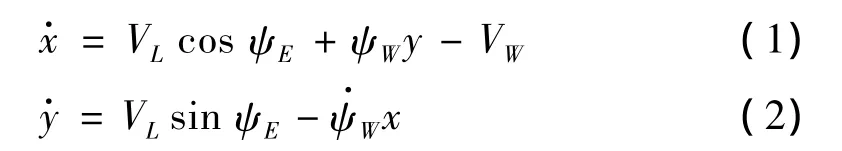
式中:Vi(i=L，W)為長機和僚機的速度;ψi(i=L，W)為長機和僚機的航向角;ψE=ψL－ψW為航向角偏差。

編隊飛行中每架UAV都安裝有編隊保持自駕儀，本文采用一階慣性環節描述，如下式所示:

式中:τVi(i=L，W)和τψi(i=L，W)分別為速度時間常數和航向角時間常數。由于本文所研究的無人機模型機動性較差，在長機進行大角度機動轉彎時，僚機無法跟隨長機機動，所以應用小擾動和小角度假設，對其進行線性化處理得:

對式(3)～式(8)進行整理，可得編隊飛行的數學模型為:

2 自抗擾編隊控制器設計

2.1 自抗擾控制算法設計

ADRC是一種新型的控制算法，它對對象模型依賴程度較低，且對于系統中的不確定干擾具有較強的抑制作用，非常適合于UAV這種動態特性比較復雜的非線性系統［8-10］。因此，本文對作為僚機的UAV的速度和航向兩個通道設計了由微分器(TD)、擴展狀態觀測器(ESO)、誤差的非線性組合(NLSEF)和擾動估計補償環節構成的ADRC控制器，如圖2所示。

圖2 自抗擾控制器結構圖Fig.2 The structure of the ADRC controller

以航向角回路為例介紹ADRC控制器的設計。由于航向角ψ和角速率q是準積分關系，令x1=ψ，x2=ψ≈q，則航向角運動方程可寫成如下形式:

自抗擾控制器的具體選擇算法如下。

2.1.1 微分器

式中:r為快速因子;h0為濾波因子;h為積分步長。r參數的選取應滿足使得跟蹤微分器響應快和在給定階躍信號時跟蹤微分器輸出曲線較為光滑兩個條件。只要 h ≤ h0，即可消除震顫。fhan(x1，x2，r，h)的算法如下:

2.1.2 擴展狀態觀測器

式中:β01，β02和β03為增益系數，其整定原則是使擴張狀態觀測器能夠很好地估計出系統各個狀態的變化和擾動，β01，β02，β03應協同調整;δ為可調參數。fal(e，α，δ)的算法為:

2.1.3 誤差的非線性組合

式中:α1，α2，α3及β1，β2，β3為可調參數;y為編隊實際距離;yc為編隊間隔指令。

2.1.4 擾動估計補償為:

式中:b為可調參數，是唯一與控制對象有關的參數，其微小變化可能引起輸出u的躍變，一般b取較大值可以有效補償擾動和不確定因素。

在上述參數條件下，對ADRC控制器參數整定如下:r=0.2，h0=1，h=1，β01=0.8，β02=0.15，β03=0.5，δ=0.1，α1=0.8，α2=0.4，α3=0.8，β1=1.1，β2=0.1，β3=0.02，b=0.1。

2.2 編隊控制系統仿真結構

用于模擬編隊飛行控制系統仿真的控制結構如圖3所示。

圖3 編隊控制系統結構Fig.3 Formation control system architecture

長機和僚機的自動駕駛儀完全獨立，飛行時由長機的自動駕駛儀發出編隊指令控制整個編隊，僚機自動駕駛儀的控制指令來自編隊控制器，編隊間隔指令和編隊控制律均在僚機模塊中執行。本文通過控制各無人機之間的編隊間隔來調整編隊的隊形，通過給各個僚機輸入編隊間隔指令(xc，yc)，各僚機控制器即可自動調整本機在編隊中的隊形，完成相應的隊形變換。

3 仿真結果及分析

UAV 一階慣性模型參數:τψW= τψL=0.05，τVW= τψL=0.1。

假設編隊時長機和僚機始終處于同一水平面內，航向角ψ0=0°，速度V=200 m/s，初始編隊x=100 m，y=300 m。

通過輸入編隊間隔指令xc=250 m，yc=500 m，僚機的編隊間隔響應如圖4所示，可知僚機成功實現了編隊的隊形變換。

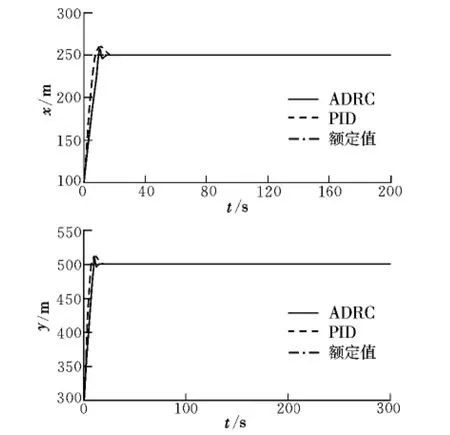
圖4 編隊隊形變換響應曲線Fig.4 The response curve of formation transforming

在仿真20 s時給予長機30°的航向角，70 s時恢復航向，速度增加至450 m/s，僚機的速度跟蹤和航向角跟蹤如圖5(a)和(b)所示，僚機x，y方向的編隊間距響應如圖5(c)和(d)所示，可知僚機成功實現了編隊的隊形保持。

圖5 編隊隊形保持響應曲線Fig.5 The response curve of formation keeping

由仿真可知，傳統PID和ADRC控制器都可以控制僚機準確跟蹤長機機動，但ADRC控制器使得僚機機動響應超調量小，x，y方向編隊調整時間較短，編隊間隔最大偏差較小且無超調，過渡更加平穩，控制效果優于PID控制。

4 結束語

自抗擾控制器可以對系統的所有不確定因素作用都歸結于“未知擾動”，并對它進行估計和補償，且無需知道系統的精準模型以及具體參數［11］，具有控制精度高、適應能力強等優點。本文所使用的方法擴充性也很好，可以通過對編隊間距的控制來實現兩架或者更多架無人機進行編隊飛行時的隊形保持與變換。在后續研究中，將深入研究各種不確定因素帶來的干擾對所設計的ADRC編隊控制器的影響，優化編隊控制器的相關參數，提高編隊控制技術的實用性。

［1］ 李文皓，張珩.無人機編隊飛行技術的研究現狀與展望［J］.飛行力學，2007，25(1):9-11.

［2］ Hasan A M，Samsudin K，Ramli A R，et al.A review of navigation systems［J］.Australian Journal of Basic and Applied Sciences，2009，3(2):943-959.

［3］ 朱戰霞，鄭莉莉.無人機編隊飛行控制器設計［J］.飛行力學，2007，25(4):22-24.

［4］ 劉成功，楊忠，樊瓊劍.無人機編隊隊形保持變換控制器設計［J］.計算機仿真，2011，28(10):73-77.

［5］ 曹宇.無人機非線性自抗擾控制方法研究［D］.哈爾濱:哈爾濱工業大學，2013.

［6］ 王曉燕，王新民，姚從潮.無人機編隊飛行神經網絡自適應逆控制器設計［J］.控制與決策，2013，28(6):837-843.

［7］ Galzi D，Shtessel Y.Closed-coupled formation flight control using Quasi-continuous high-order sliding-mode［C］//American Control Conference.New York，2007:1799-1804.

［8］ 劉剛，王彪.PID/ADRC控制器在四旋翼無人飛行控制中的應用［J］.云南民族大學學報:自然科學版，2014，23(2):151-156.

［9］ HU Q，FEI Q，WU Q，et al.Research and application of nonlinear control techniques for quadrotor UAV［C］//第三十一屆中國控制會議.合肥:中國科學技術大學，2012:706-710.

［10］楊瑞光，孫明瑋，陳增強.飛行器自抗擾姿態控制優化與仿真研究［J］.系統仿真學報，2010，22(11):2689-2693.

［11］ 韓京清.自抗擾控制技術［J］.前沿科學，2007，1(1):24-31.