有點火窗口限制的ALCM下滑段多約束制導策略

胡錦川，陳萬春

(北京航空航天大學 宇航學院，北京100191)

0 引言

空射巡航導彈(ALCM)的縱向彈道一般分為下滑段、平飛段和俯沖段。下滑段是指從載機投放至拉平點火之間的彈道，不僅需滿足彈道拉平和點火窗口要求，還需滿足臨界馬赫數、迎角和過載等過程約束。合理設計下滑段的制導策略，不僅可以增大ALCM的可投放區，還對保證ALCM點火和順利轉平具有重要意義。

傳統的下滑段制導主要采用跟蹤制導方法，該方法分為標準彈道設計和跟蹤制導律設計兩部分。其中標準彈道主要通過方案彈道規劃［1-4］和彈道優化［5-6］獲得，而跟蹤制導律的設計方法則包括PID經典控制方法［7-8］、反饋線性化［9］和在線軌跡更新［10］等。跟蹤制導依賴于標稱軌跡，并且在大擾動下的精度相對較差。基于最優控制的顯式制導策略［11-14］是解決下滑段制導問題的最新方法，具有適應性強、魯棒性好的特點。Ohlmeyer等［11］提出的廣義顯示制導律能夠同時滿足脫靶量和碰撞角約束，同時使得終端法向加速度收斂到零。Xing等［12］提出的分段最優制導律，能同時滿足終端位置、彈道傾角和迎角要求，并考慮了一階延遲環節。

本文在上述顯式制導律的基礎上，進一步加入了終端地速約束，獲得了能夠同時滿足終端高度、彈道傾角、地速和迎角約束的最優法向加速度，同時還閉環考慮了多種過程約束和風干擾的影響，最終獲得了滿足多約束要求的下滑段制導策略。

1 問題建模

1.1 運動建模

地面坐標系下，ALCM下滑段縱平面運動方程如下:

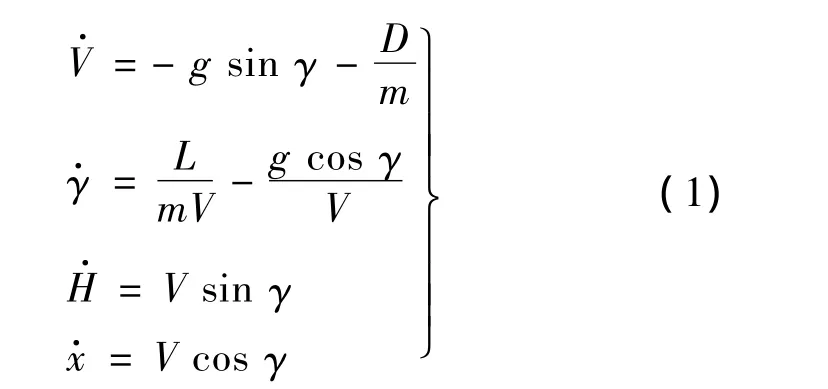
式中:V，γ，H，x分別為地面坐標系下的速度(簡稱地速)、彈道傾角、高度和縱程;g為重力加速度;m為質量;L和D分別為升力和阻力，其表達式為:

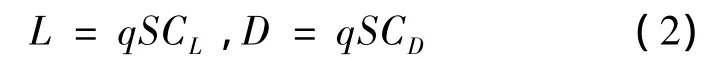
式中:S為氣動參考面積;CL和CD分別為升力系數和阻力系數，與馬赫數Ma和迎角α相關;q為動壓:

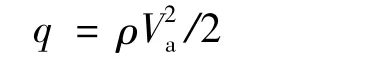
式中:ρ為大氣密度;Va為空速，其與地速的關系為:

式中:Vws為風速在射面內的分量。

1.2 約束建模

ALCM在下滑段同時包含多個終端約束和過程約束。

1.2.1 臨界馬赫數約束

ALCM在下滑過程中，空速馬赫數不能超過臨界馬赫數，否則其氣動特性將會急劇地變壞，使操縱困難。臨界馬赫數約束如下:

式中:Maa為空速馬赫數(Maa=Va/c，c為聲速);Macr為臨界馬赫數。

1.2.2 控制能力約束

ALCM下滑段經歷的空域非常大，動壓變化大，導致可用過載變化范圍大。因此ALCM需同時考慮迎角范圍約束和可用過載約束:

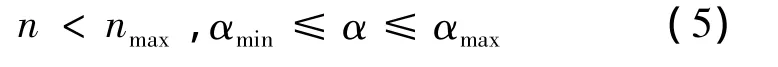
式中:n為法向過載，n=L/(mg);nmax，αmin和 αmax分別為最大可用法向過載、最小可用迎角和最大可用迎角。

1.2.3 點火窗口約束

以航空發動機為動力的ALCM需保證點火時進氣道氣流充足且穩定，因此下滑段的終點需滿足點火窗口約束:

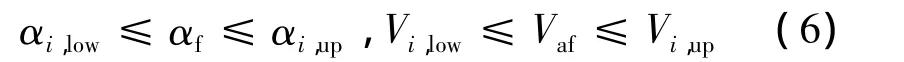
式中:αf和 Vaf分別為終端迎角和空速;αi，low，αi，up，Vi，low，Vi，up分別為最小點火迎角、最大點火迎角、最小點火空速和最大點火空速，它們均與點火高度(Hi)相關，如圖1所示。

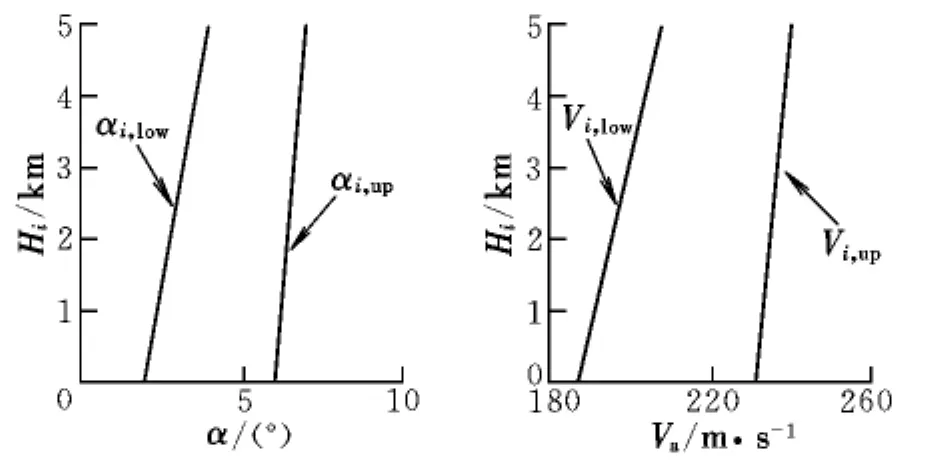
圖1 點火窗口Fig.1 Ignition window

在制導時，為了保證擾動下終端迎角和空速能夠滿足點火窗口要求，αf和Vaf通常取點火窗口的中間值:

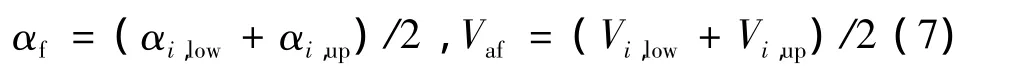
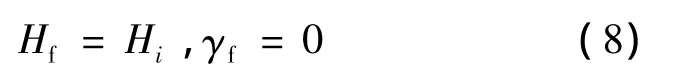
式中:Hf和γf分別為終端高度和彈道傾角。

1.2.4 飛行時間約束

ALCM快速下滑有助于提高其隱蔽性，同時彈載電源也要求導彈的下滑時間不能過長，因此飛行時間需滿足如下約束:

式中:tmax為最大飛行時間。

1.3 風場建模

在下滑段的制導中，臨界馬赫數約束和終端約束均涉及空速。但考慮到隱身等要求，ALCM往往不安裝空速管，使得飛行過程中空速無法測量，只能利用慣導獲得的地速信息來估算其大小。若完全忽略風干擾的影響，則可能造成空速的散布范圍大于點火空速窗口，如圖2所示(地速取中間空速時風干擾下的空速散布范圍)，因此需要通過估算風速來減小估算空速的散布［15-17］。

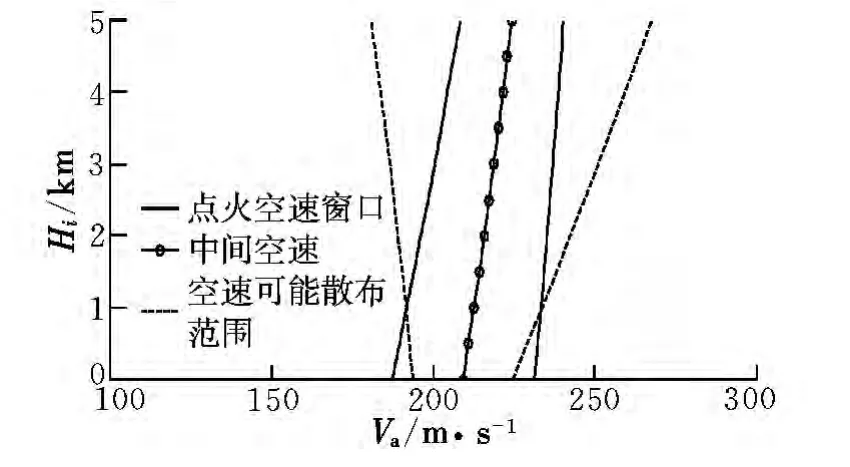
圖2 風干擾對空速的影響Fig.2 The effect of wind interference on airspeed

忽略隨機變化的突風影響，對流層射面內的平均風廓線近似滿足如下關系:

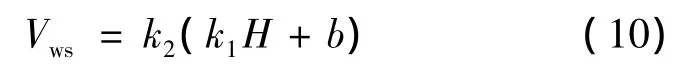
式中:k1和b為準定常風模型的參數;k2為修正系數。由投放時刻載機獲得的射面風速信息估得:

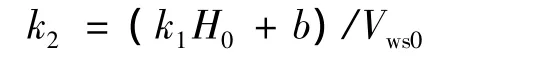
式中:H0為投放高度;Vws0為投放時載機測得的射面風速。

利用上述風場模型，可將點火空速約束和臨界馬赫數約束轉化為點火地速約束和最大地速約束:

式中:Vf為終端地速;Vi和Vmax分別為點火地速和臨界馬赫數確定的最大地速:

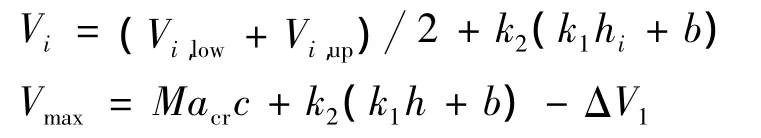
式中:ΔV1為考慮風速誤差的速度安全余量。

2 下滑段多約束制導策略

2.1 制導策略

下滑段的約束可分為三大類:第一類為終端約束，包括終端高度、彈道傾角、地速和迎角約束;第二類為與制導指令相關的過程約束，包括臨界馬赫數約束、迎角約束和法向過載約束;第三類為飛行時間約束。根據上述各類約束的特點，設計如下制導策略:

(1)第一類約束關系到能否順利點火，決定了制導指令的基本形式，將采用最優控制理論進行求解;

(2)第二類約束關系到飛行品質，決定了制導指令的邊界;

(3)由于下滑段存在很強的速度約束，因此飛行時間可調的范圍較小，在制導時可忽略其影響，但飛行時間約束會影響可投放區的大小。

2.2 多終端約束優化問題建模

忽略過程約束影響，下滑段制導幾何關系如圖3所示。圖中，an為法向加速度，將作為下滑段的制導指令，an=L/m －g cosγ。

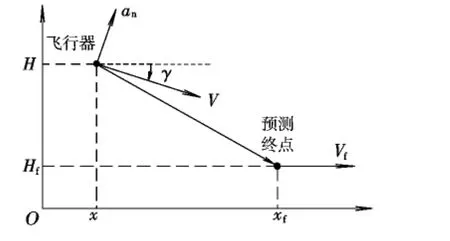
圖3 制導幾何關系Fig.3 Guidance geometry

下滑段制導問題的難點在于同時滿足終端地速大小和方向的要求，為此，需要對速度微分方程進行線性化［18］。引入比能量e=V2/2+gh，對時間求導可得:

在下滑段ALCM處于自由滑翔狀態，升阻比變化不劇烈。若假設在飛行過程中升阻比不變，則阻力可寫為:

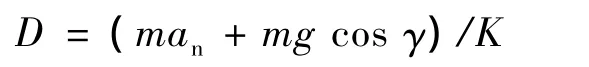
式中:K為下滑段的升阻比，在計算時取常值。將上式帶入式(13)可得:

以x為自變量，并假設γ為小量，則由式(1)和式(14)可得下滑段線性化的運動方程為:

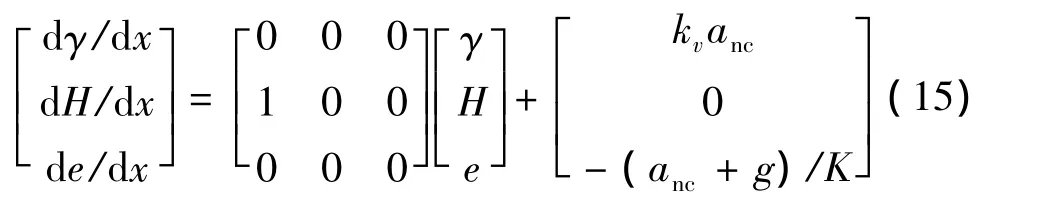
式中:kv=1/V2，設為常數;anc為僅考慮終端過程約束情況下的法向加速度，為控制變量;γ，H和e為狀態變量，其終端約束為:

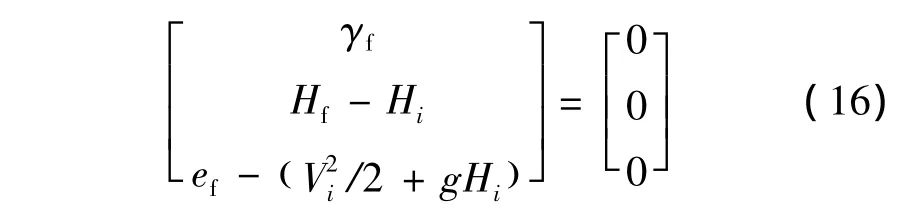
設目標函數為:

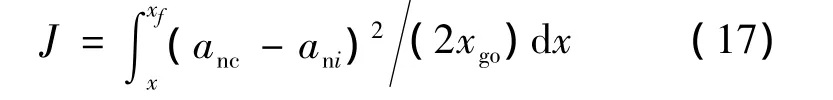
式中:xgo為剩余縱程;ani為點火迎角對應的法向加速度，它們分別滿足如下關系式:

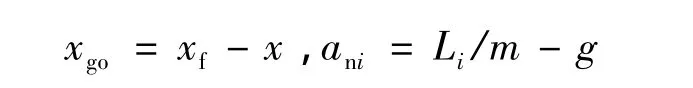
式中:xf為終端縱程;Li為迎角取(αi，low+ αi，up)/2 時對應的升力。式(17)給出的目標函數可使得在x→xf的時候anc→ani，從而保證終端迎角滿足要求。

利用上述優化模型，可以獲得同時滿足下滑段點火點的高度、彈道傾角、地速和迎角要求的anc。

2.3 滿足多終端約束的最優法向加速度

引入哈密爾頓函數:

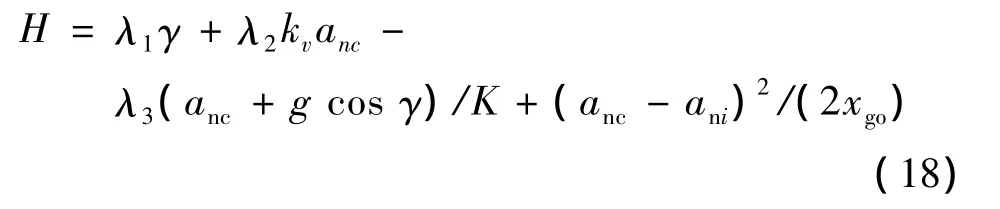
式中:λ1，λ2和λ3分別為H，γ和e對應的協態變量，滿足如下關系:

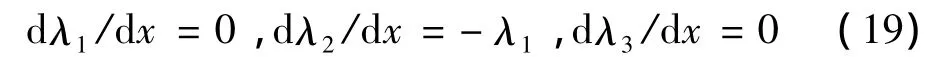
求解式(19)可得:

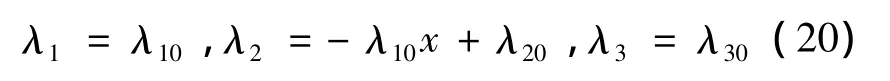
式中:λ10，λ20和 λ30為協態初值。

最優法向過載滿足:

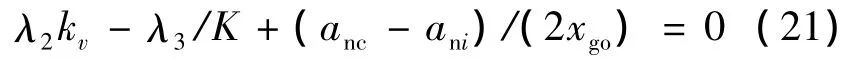
將式(20)帶入式(21)并整理得:

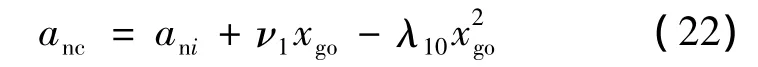
式中:ν1=(λ10xf－λ20)kv+λ30/K。將式(22)帶入

式(15)，并結合式(16)可得最優法向加速度為:

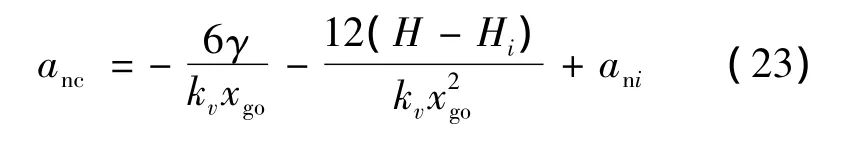
其中:

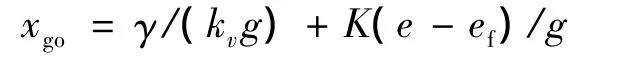
2.4 法向加速度邊界

法向加速度邊界由臨界馬赫數約束、迎角約束和法向過載約束共同確定。

2.4.1 臨界馬赫數約束

式(12)將臨界馬赫數約束轉化為最大地速約束。為了滿足該約束，當V逐漸接近Vmax，則需逐漸減小至零。由于法向過載越大則越小，因此該約束對應著法向過載下邊界，其表達式如下:

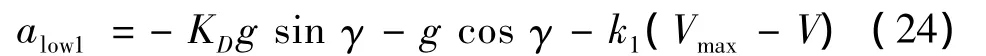
式中:KD為D=－mg sinγ對應的升阻比;k1為制導指令光滑因子:

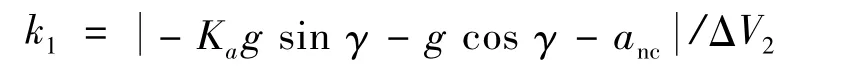
式中:ΔV2為速度常數。

2.4.2 迎角約束

最大迎角約束和最小迎角約束分別對應著法向加速度的上邊界和下邊界，如下所示:

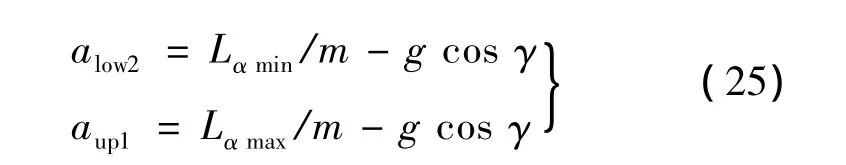
式中:Lαmin和Lαmax分別為αmin和αmax對應的升力。

2.4.3 過載約束

過載約束對應著法向加速度的上邊界:

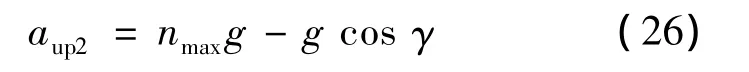
2.4.4 法向加速度邊界

總的來說，法向加速度邊界為:

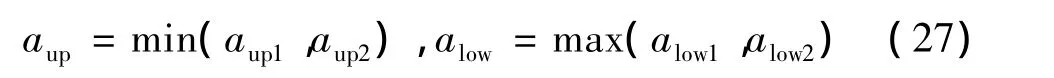
式中:aup和alow分別為下滑段法向加速度的上邊界和下邊界。

2.5 下滑段制導指令

綜上可得，多約束條件下的下滑段制導指令為:

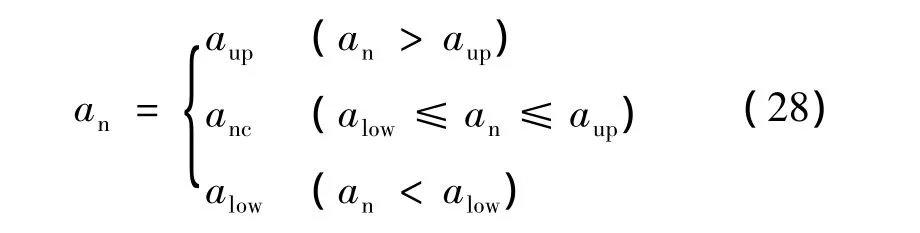
式中:an為下滑段法向加速度。

3 仿真校驗

3.1 模型建立

為了校驗上述下滑段制導策略的性能，選用戰斧巡航導彈作為仿真模型，具體參數見表1。

表1 仿真參數Table 1 Simulation parameters

此外，導彈的氣動數據采用Datcom估算，擬合如下:

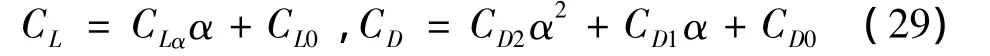
其中:

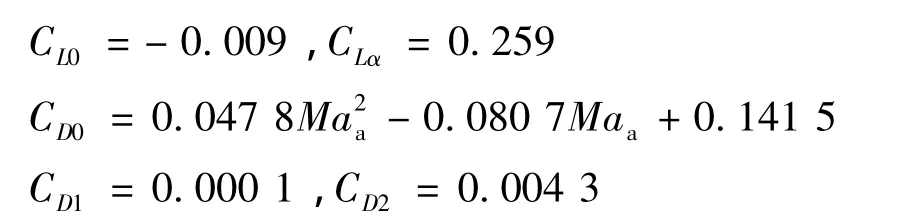
3.2 下滑段多約束制導策略仿真驗證

為了驗證本文給出的下滑多約束制導策略的性能，將制導結果與打靶法優化結果進行了對比，其中打靶法的目標函數與式(17)相同。仿真條件見表2，結果如圖4～圖6所示。

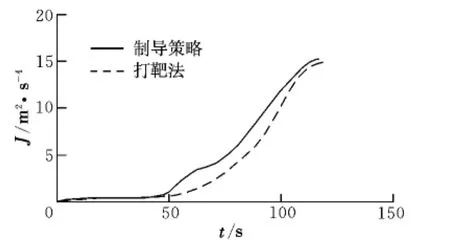
圖4 目標函數曲線Fig.4 Target function histories

由圖4可以看出，由打靶法獲得的最優解目標函數終值為15.03 m2/s4，而由制導策略得到的目標函數終值為15.35 m2/s4，兩者僅相差2%。

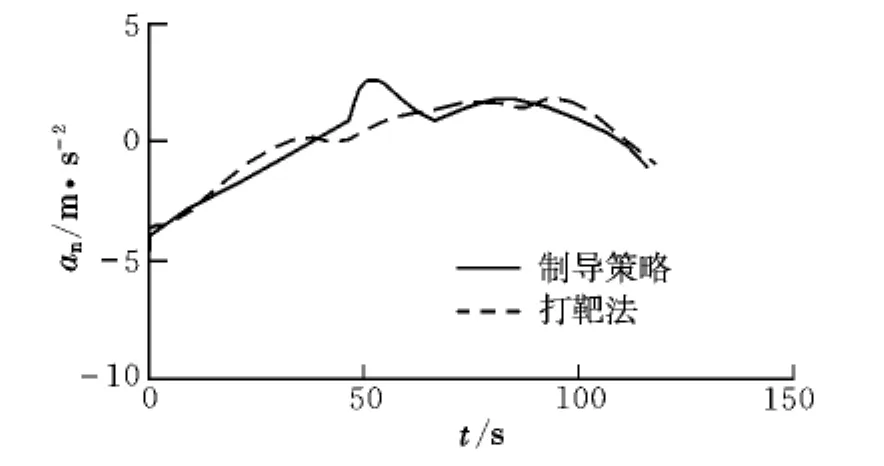
圖5 法向加速度曲線Fig.5 Normal acceleration histories

由圖5可以看出，本文制導策略的加速度曲線與優化曲線基本重合，但存在一個凸起，這是由于該處的空速接近臨界馬赫數，制導指令中考慮了速度限制的影響。

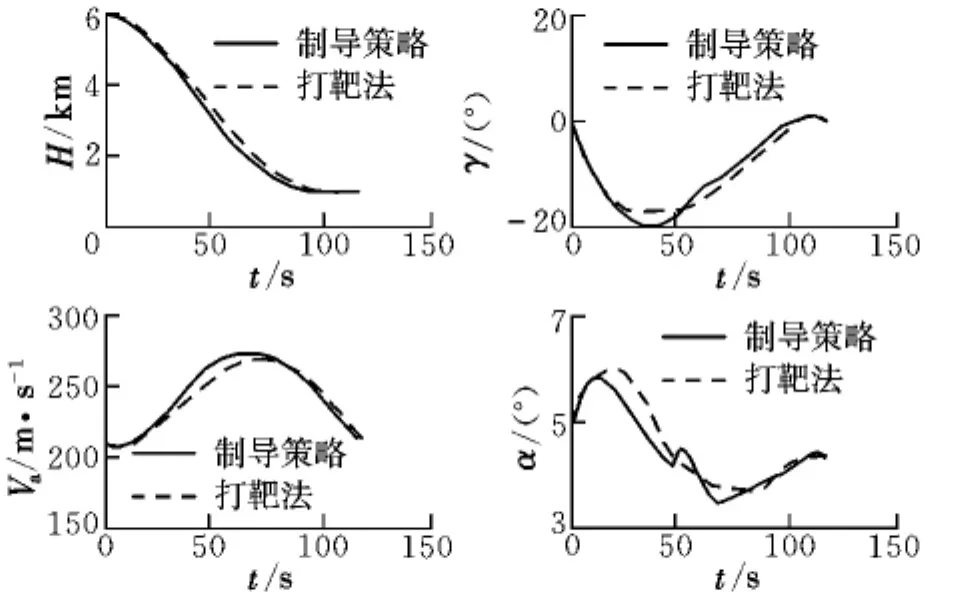
圖6 狀態和迎角曲線Fig.6 States and angle of attack histories

由圖6可以看出，制導策略獲得的高度、彈道傾角、空速與迎角曲線均與打靶法的結果較為接近，均滿足終端約束要求。

3.3 綜合拉偏打靶

設飛行任務和拉偏參數如表3所示。

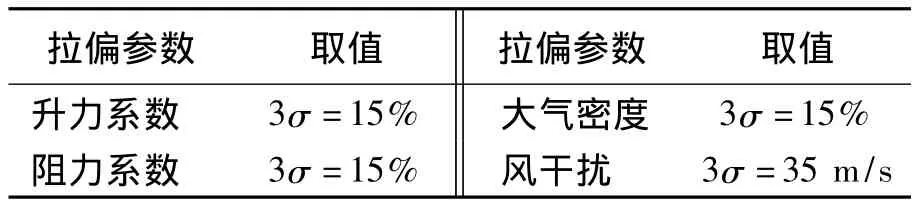
表3 拉偏設置Table 3 Disturbance conditions

分別采用本文制導策略和PID跟蹤制導策略(打靶法優化結果)對滑翔段彈道進行1 000次打靶，得到的結果如圖7～圖10所示。圖中，左子圖為本文制導策略結果，右子圖為打靶法結果。

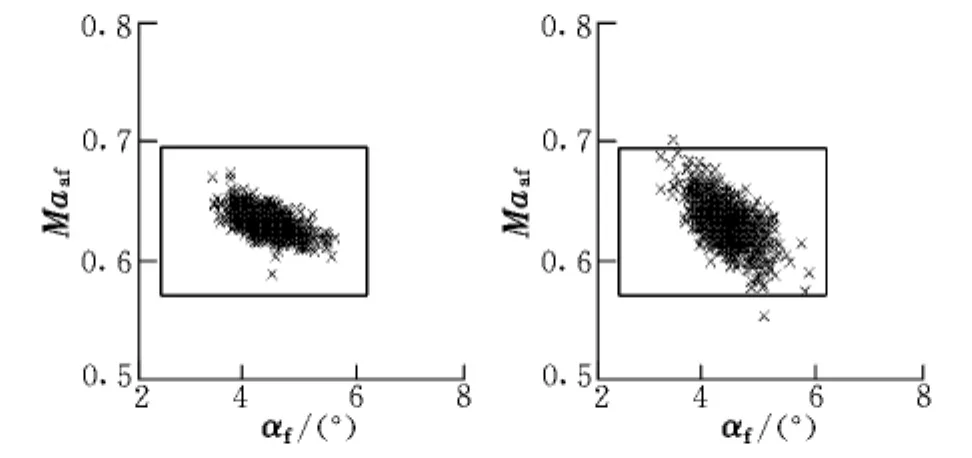
圖7 終端迎角和馬赫數散布Fig.7 Final angles of attack and airspeed Mach

由圖7可以看出，本文制導策略獲得的終端迎角和空速馬赫數均滿足點火窗口要求，并且散布相對較小;而跟蹤制導策略則有可能不滿足點火窗口要求，并且散布相對較大。

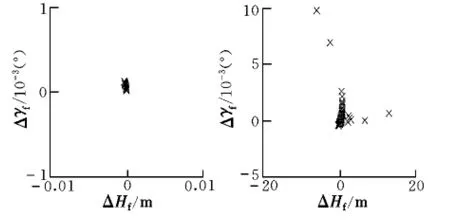
圖8 終端高度和彈道傾角誤差Fig.8 Final height errors and ballistic bank errors

由圖8可以看出，本文制導策略的終端高度和彈道傾角精度要優于跟蹤制導策略。

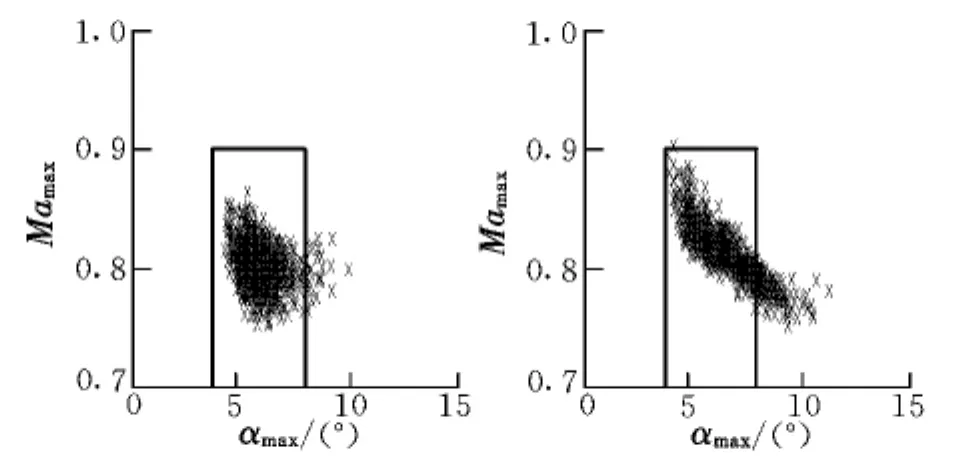
圖9 最大迎角和空速馬赫數散布Fig.9 Maximum angle of attack and airspeed Mach

由圖9可以看出，兩種制導策略均存在不滿足過程約束的情況，但本文制導策略97.6%的概率滿足過程約束要求，而跟蹤制導策略只有84.0%的概率滿足過程約束要求。

圖10進一步分析了風干擾對迎角和空速的影響。可以看出，風干擾的附加迎角Δαw可達4°，馬赫數增量ΔMaa可達0.1，這也是存在較多不滿足過程約束算例的主要原因。

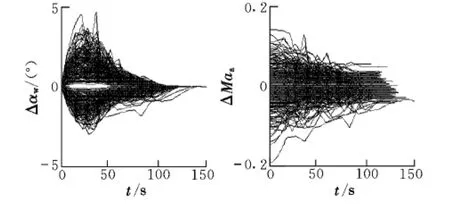
圖10 風干擾對迎角和空速的影響Fig.10 Impact of wind interference on angle of attack and airspeed

總的來說，相對于跟蹤制導策略，本文制導策略具有抵抗拉偏能力強、魯棒性好的特點。

3.4 可投放區

利用本文提出的ALCM下滑段多約束制導策略，進一步求解可投放區，得到的結果如圖11和圖12所示。

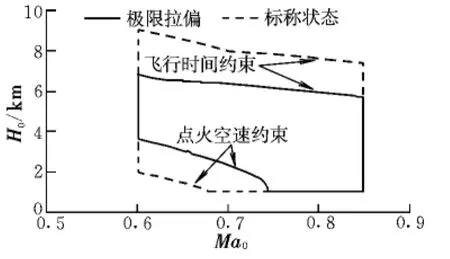
圖11 低空點火可投放區Fig.11 Acceptable launching region of low altitude

圖12 高空點火可投放區Fig.12 Acceptable launching region of high altitude

由圖可知:可投放區的下界由點火空速決定，可投放區的上界在低空點火時由飛行時間約束決定，高空點火時由飛行時間及臨界馬赫數約束共同決定;拉偏會減小可投放區，并且高空點火的影響要大于低空點火;高速投放比低速投放具有更寬的允許投放高度范圍。

4 結束語

本文提出了一種ALCM下滑段多約束制導策略。在空速不可測的情況下，提出通過風廓線和地速估算空速的方法，能夠有效降低風干擾帶來的終端空速散布，從而滿足ALCM點火窗口要求。將臨界馬赫數約束、迎角約束和過載約束轉化為法向加速度邊界，實現了對過程約束的閉環考慮。獲得了下滑段最優法向加速度，能夠同時滿足終端高度、彈道傾角、地速和迎角約束。仿真驗證表明，該制導策略獲得的結果與打靶法優化結果類似。在氣動力拉偏、大氣密度拉偏和風干擾的情況下，與傳統的PID跟蹤法相比，具有更高的制導精度和更好的魯棒性。利用該制導策略，給出了ALCM的可投放區，并分析了拉偏對可投放區的影響，為實際應用提供了理論依據。

［1］ Tsikalas G M.Space shuttle auto land design［R］.AIAA-82-1604，1982.

［2］ Barton G H，Tragesser SG.Auto landing trajectory design for the X-34［R］.AIAA-99-4161，1999.

［3］ 彭紹雄，周卿吉.空艦導彈彈道優化算法［J］.戰術導彈技術，1990(1):19-26.

［4］ 楊劍影，謝邦榮，尹健.中程空地導彈下滑彈道的設計方法探究 ［J］.彈箭與制導學報，2003，23(3):50-52.

［5］ 周浩，周韜，陳萬春.高超聲速滑翔飛行器引入段彈道優化 ［J］.宇航學報，2006，27(5):970-973.

［6］ 周國鋒，王朝志，陳萬春.機動彈頭引入段彈道優化設計［J］.戰術導彈技術，2008(5):20-23.

［7］ Miyazawa Y，Motoda T，Izumi T，et al.Longitudinal landing control law for an autonomous reentry vehicle［J］.Journal of Guidance，Control，and Dynamics，1999，22(6):792-800.

［8］ 劉瑋，宋科璞.飛行器無動力下滑技術研究［J］.計算機仿真，2013，30(8):65-69.

［9］ 李雪松，李穎暉，徐浩軍，等.基于直接反饋線性化的飛行器著陸控制設計［J］.飛行力學，2010，28(4):42-45.

［10］ Schierman J D，Hull J R，Ward D G.Adaptive guidance with trajectory reshaping for reusable launch vehicles［R］.AIAA-2002-4458，2002.

［11］ Ohlmeyer E J，Philips C A.Generalized vector explicit guidance［J］.Journal of Guidance，Control，and Dynamics，2006，29(2):261-268.

［12］ Xing Qiang，Chen Wanchun.Segmented optimal guidance with constraints on terminal angle of attack and impact angle［R］.AIAA-2012-0257，2012.

［13］ Lee Y I，Kim SH，Lee J I.Analytic solutions of generalized impact-angle-control guidance law for first-order lag system ［J］.Journal of Guidance，Control，and Dynamics，2013，36(1):96-112.

［14］趙漢元，陳克俊.再入機動彈頭的速度控制［J］.國防科技大學學報，1993，15(2):11-17.

［15］肖業倫，金長江.大氣擾動中的飛行原理［M］.北京:國防工業出版社，1993:11-18.

［16］ Oznur Usanmaz，Enis T T.Wind effect analysis on instrument flight procedures using a Turkish wind model［J］.Journal of Aircraft，2012，39(6):2023-2032.

［17］張松蘭，劉曉利.風場建模與彈道仿真［J］.彈箭與制導學報，2006，26(1):550-552.

［18］ Mease K D，Chen D T，Sch?nenberger H.Reduced order entry trajectory planning for acceleration guidance［J］.Journal of Guidance，Control，and Dynamics，2002，25(2):257-266.