增穩錐套與軟管二級擺建模與仿真

石超，薛建平，董新民，王健，陳勇

(空軍工程大學 航空航天工程學院，陜西 西安710038)

0 引言

對于“插頭-錐套”自主空中加油方式來說，由于存在大氣紊流［1］與受油機前體產生的頭波［2］影響，再加上加油軟管的柔性，導致加油錐套相對于加油機的空間位置不能固定，在一定范圍內存在飄擺現象。由此可知，該加油方式存在兩個缺點［3-4］:一是由于錐套存在飄擺現象，導致加油對接環節的時間較長;二是受油機接近加油錐套時，其前體頭波可能誘發加油錐套震蕩從而導致相關的加油事故。因此，增穩錐套的概念便應運而生。

Ellsworth等［5］早在1976年就著手研究對空中加油錐套進行引導與控制，設計出了一種用氣動控制面代替穩定傘的加油錐套，并搭載在加油機CC-137上進行了一系列飛行試驗。Williamson等［3］研究了通過操縱穩定傘對錐套進行主動增穩控制的設想，在低速錐套的基礎上制造出一個可控錐套進行風洞試驗，并通過控制方法的仿真獲得了良好的控制效果。胡孟權等［6］通過對加油軟管運動規律及平衡拖曳位置的研究，分析了軟管的運動規律和錐套姿態的變化規律。王海濤等［7］針對軟管錐套式空中加油系統的軟管建模問題，提出了一種可變長度的多級串聯理想單擺系軟管運動模型，分析了加油機尾渦流場、滾轉運動對軟管錐套的動態影響及軟管甩鞭現象的產生原因，并通過MATLAB仿真驗證了所建模型的有效性。

對增穩錐套概念設計的研究文獻越來越多，但都沒有一個較好的仿真驗證平臺。雖然這些文獻對軟管錐套系統進行了分段建模研究，但大多把錐套視為一個只有氣動阻力的質點。為此，本文提出了適用于仿真與風洞試驗研究的增穩錐套與軟管二級擺模型。此模型著重研究了增穩錐套的氣動特性，而將軟管視為等長的剛體桿。通過對此模型的建模與仿真研究，最終，獲得了穩定氣流中增穩錐套的靜力平衡位置，為增穩錐套的進一步主動增穩控制方法研究奠定了仿真驗證平臺基礎。

1 增穩錐套氣動系數獲取

1.1 增穩錐套三維數字模型的建立

本文所涉及到的增穩錐套模型的實物錐套原型如圖1所示。

圖1 軟管式空中加油錐套Fig.1 Drogue in air refueling hose-drogue systems

本文結合圖1中的加油錐套與文獻［8］中風洞試驗的905550錐套模型，使用三維數字固體幾何建模軟件UG建立了有8根支柱的簡化三維數字錐套模型，并給出了一種加裝“十字形”控制舵面增穩控制錐套的概念設計模型，如圖2所示。

圖2 普通錐套與加裝舵面的增穩錐套三維模型Fig.2 3D models of drogue and stability drogue with control surfaces

1.2 CFD數值計算方法獲取氣動系數

1.2.1 數值計算結果

在Ma=0.4無干擾自由來流條件下，本文采用CFD方法分別計算了增穩錐套在6種迎角下的阻力系數CD、升力系數CL以及俯仰力矩系數Cm，所有計算中舵偏均為零。由于在實際加油條件下，錐套的迎角不超過5°，故選取 α =0°，1°，2°，3°，4°，5°這6 個迎角條件進行數值計算。在錐套體坐標系內，CFD數值計算所得6種迎角下增穩錐套的阻力系數、升力系數及俯仰力矩系數如表1所示。

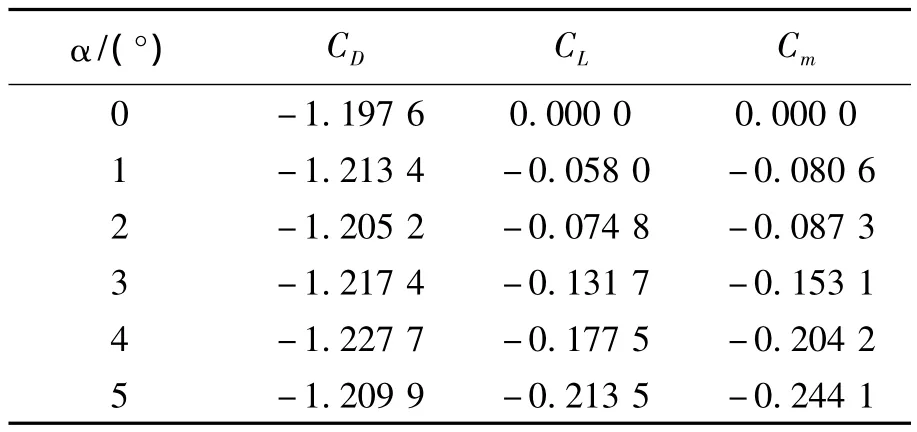
表1 增穩錐套在不同迎角下的氣動系數Table 1 Aerodynamic coefficients of stability augmentation drogue at different angle of attack

圖3和圖4分別為增穩錐套在不同迎角下的阻力系數曲線、升力系數曲線及俯仰力矩系數曲線。

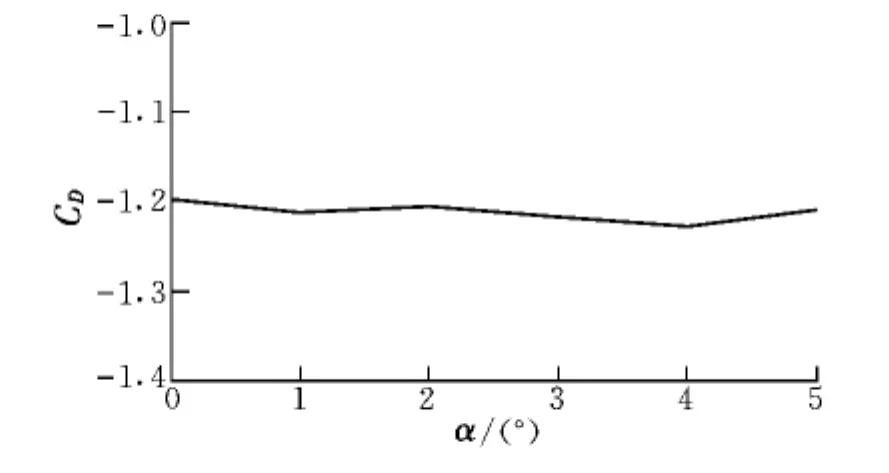
圖3 增穩錐套在不同迎角下的阻力系數曲線Fig.3 Drag coefficient curve of stability augmentation drogue at different angle of attack

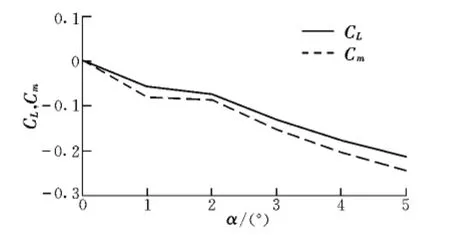
圖4 增穩錐套在不同迎角下的升力系數和俯仰力矩系數曲線Fig.4 Curves of lift and pitch moment coefficient of stability augmentation drogue at different angle of attack

1.2.2 CFD方法的有效性驗證

本文將錐套穩定傘阻力系數作為驗證對象。根據文獻［8］給出的經驗公式可知，本文錐套穩定傘阻力系數的預測值為:

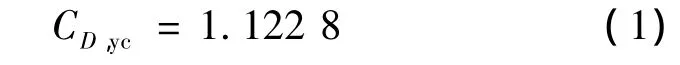
其與計算所得穩定傘阻力系數的平均值1.163 6誤差3.63%，足以說明本文所用CFD方法的有效性。

1.3 氣動系數線性擬合

由圖3和圖4可知，迎角在0°～5°內，增穩錐套阻力系數、升力系數及俯仰力矩系數均與迎角呈近似線性關系。故采用一元線性回歸方法［9］分別對這三個系數進行線性擬合。擬合結果為:

2 二級擺運動建模

2.1 建模假設與坐標定義

在給出“軟管-錐套”二級擺模型前，為了簡化所研究問題的復雜性，進行如下假設:加油機定直平飛;將軟管視為等長剛體管，并忽略其氣動特性;認為地面坐標系為慣性坐標系;剛體管與加油吊艙間用假設的球形接頭連接。增穩錐套與軟管二級擺模型如圖5所示。

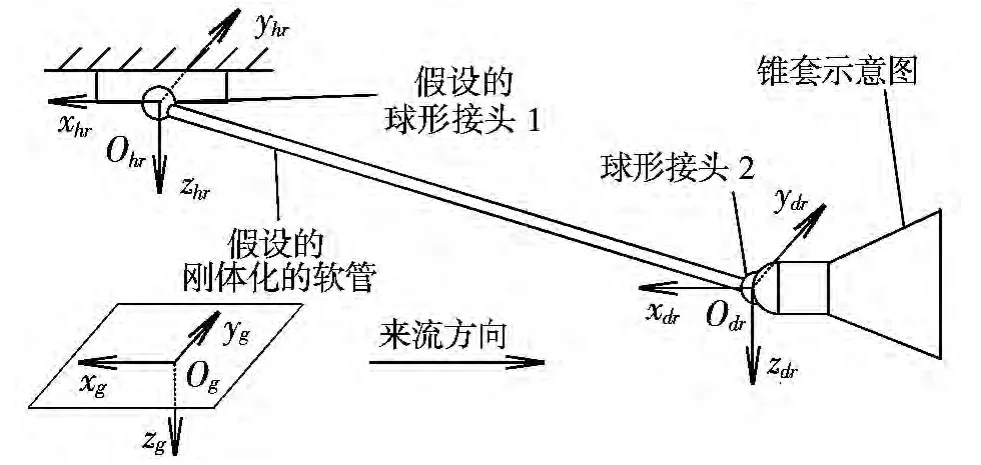
圖5 二級擺模型及坐標關系示意圖Fig.5 Schematic diagram of the double pendulum model and coordinate system

如圖5所示，令地軸系Ogxgygzg為慣性系，管參系Ohrxhryhrzhr與錐參系Odrxdrydrzdr的原點分別為球形接頭1與2的球心，且都與慣性系平行。本文研究還涉及到錐體系Odxdydzd與管體系Ohxhyhzh。錐體系原點與錐參系相同，xd軸與錐套中軸線重合，指向剛體管為正，yd軸與慣性系yg平行，zd由右手定則確定。管體系與錐體系定義方法相同，其原點在球形接頭1球心處。

2.2 動力學方程

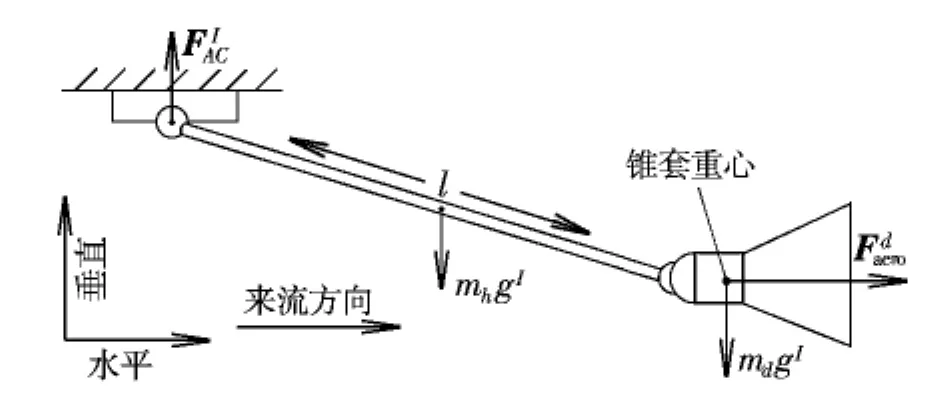
圖6 二級擺動力學模型平面示意圖Fig.6 Schematic diagram of vertical plane of the double pendulum dynamics model

作用在球形接頭1球心處的合力與合力矩方程分別為:

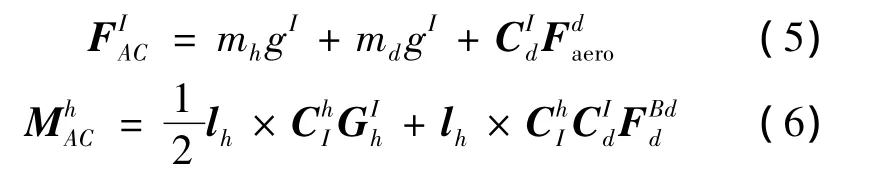
作用在球形接頭2球心處的合力與合力矩方程為:

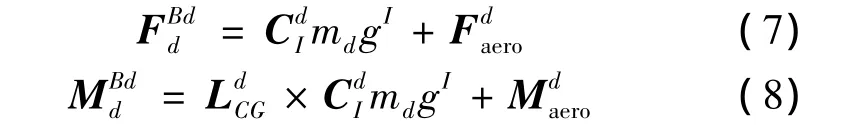
增穩錐套繞球形接頭2球心轉動的動力學微分方程為:

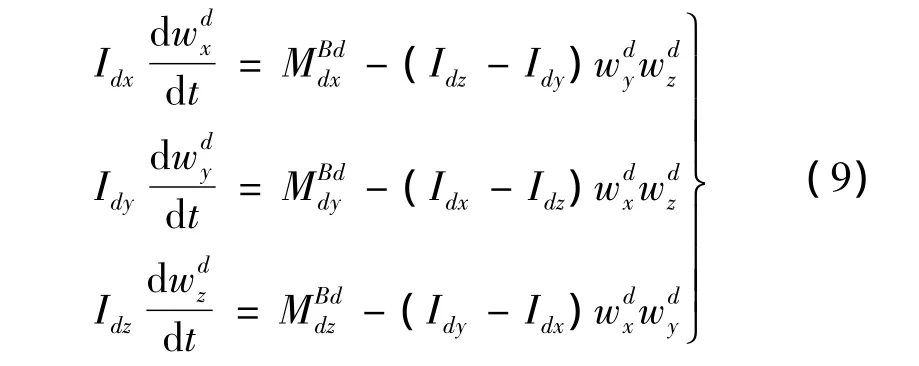
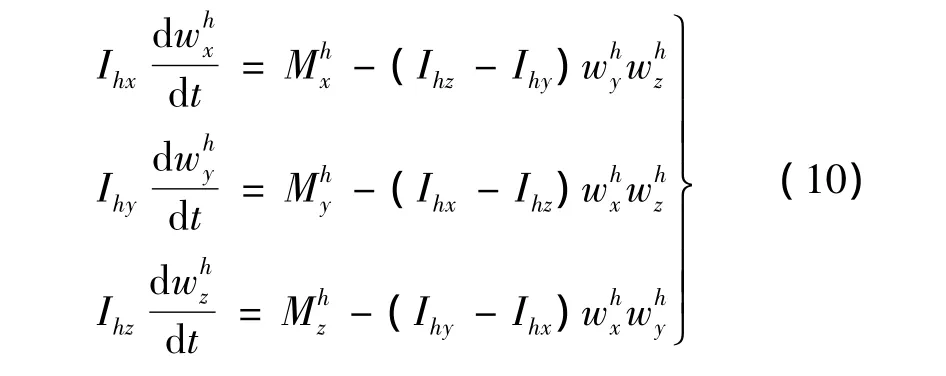
剛體管繞球形接頭1球心轉動的動力學微分方程為:式中:Ihx，Ihy，Ihz為剛體管繞其三個慣性主軸(在管體系內)的轉動慣量為剛體管繞接頭1球心的合力矩在管體系三個主軸上的分量;為剛體管繞其三個主軸的轉動角速度分量。

2.3 運動學方程

本文采用四元數［10］解算剛體管與增穩錐套姿態。管參系中，剛體管繞球形接頭1球心轉動的四元數微分方程為:

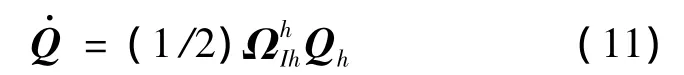
式中:Qh為剛體管單位四元數姿態為剛體管角速度矢量四元數矩陣形式，其表達式為:

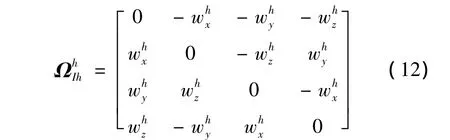
錐參系中，增穩錐套繞球形接頭2球心轉動的四元數微分方程為:

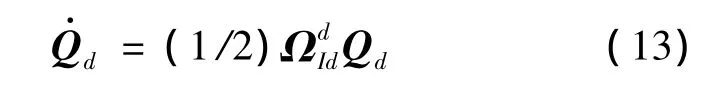
式中:Qd為剛體管單位四元數姿態;為增穩錐套角速度矢量的四元數矩陣形式，其表達式為:

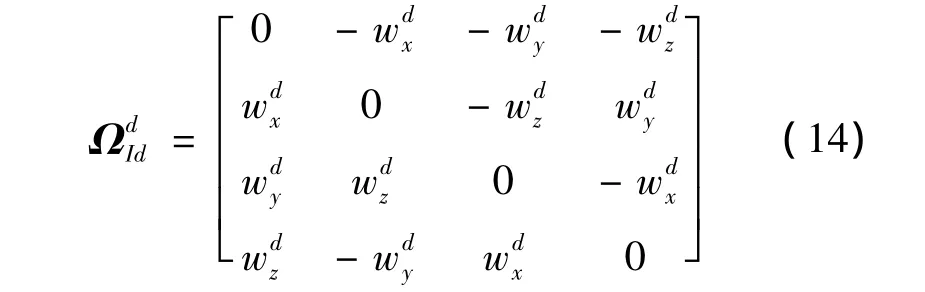
給定增穩錐套和剛體管的初始位姿，聯立求解式(9)～式(11)及式(13)，即可計算出二級擺模型實時位姿。

3 仿真結果及分析

根據以上二級擺運動模型搭建Simunlink仿真模型。本文通過管參系Ohrxhrzhr平面內二級擺運動仿真，旨在獲得穩定來流中增穩錐套相對于加油機吊艙的穩定平衡位置。

增穩錐套與剛體管的特性參數如下:剛體管長度30.48 m;剛體管直徑0.08 m;剛體管滿油密度6.64 kg˙m－1;增穩錐套質量32.09 kg;增穩錐套xd軸重心位置0.44 m。

仿真初始條件如下:穩定來流馬赫數Ma=0.4;剛體管初始俯仰角20°;增穩錐套初始俯仰角0°;剛體管初始俯仰角速度0 rad˙s－1;增穩錐套初始俯仰角速度 0 rad˙s－1。

在初始條件下，使用擬合所得氣動系數和二級擺特性參數進行仿真，得到管參系Ohrxhrzhr平面內錐套重心運動軌跡，如圖7所示。

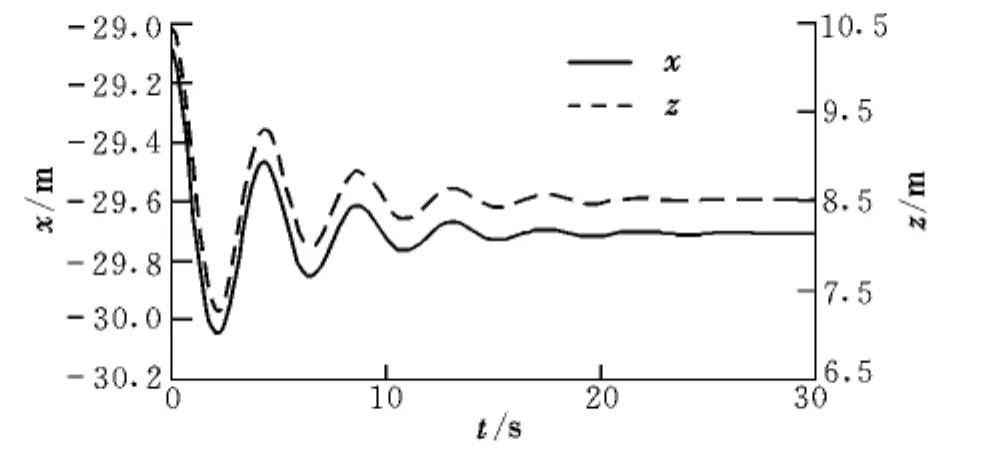
圖7 增穩錐套重心運動軌跡Fig.7 Trajectory of the center of stability drogue gravity

由圖7可知，仿真進行了30 s后，增穩錐套處于穩定平衡狀態。表2給出了管參系內二級擺穩定參數。

表2 二級擺穩定參數Table 2 Stability parameters of double pendulum

為了驗證穩定參數的可靠性，將穩定俯仰角與俯仰角速度作為初始條件，再次進行仿真，得到管參系Ohrxhrzhr平面內增穩錐套重心運動軌跡如圖8所示。

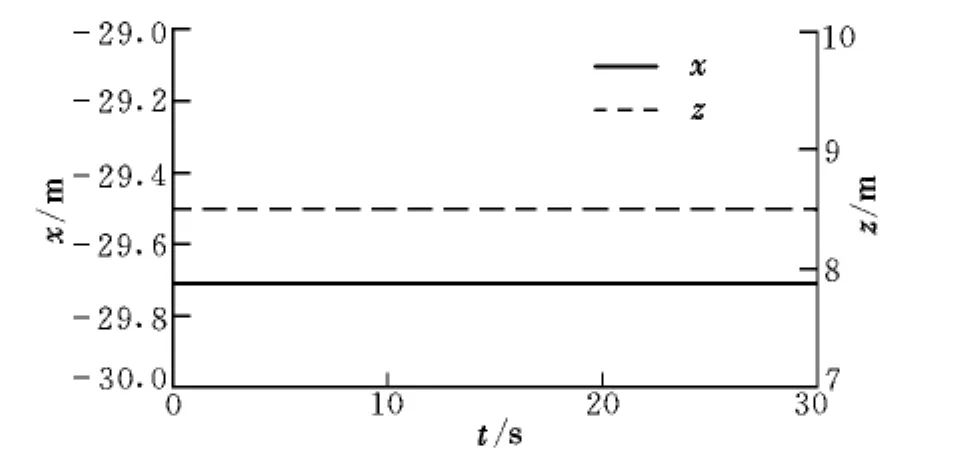
圖8 增穩錐套重心運動軌跡Fig.8 Trajectory of the center of stability drogue gravity

從圖8可以看出，仿真獲得的穩定參數可靠，同時也說明了所搭建的增穩錐套二級擺仿真驗證平臺的有效性。

4 結束語

本文提出了一種簡化的軟管與增穩錐套二級擺模型，建立了其運動模型，并進行了仿真研究，最終獲得了穩定氣流中增穩錐套的穩定平衡位置，為增穩錐套的進一步主動增穩控制方法研究奠定了仿真驗證平臺基礎。下一步的工作可在如下兩方面開展:研究在不同迎角與不同舵偏角下，增穩錐套的氣動特性，為其增穩控制提供氣動參數;在其氣動特性充分研究的基礎上，研究增穩錐套的控制算法，達到穩定錐套的目的。

［1］ 張雷雨，張洪，楊洋，等.空中加油對接過程的動力學建模與仿真［J］.航空學報，2012，33(7):1347-1354.

［2］ Dogan A，Blake W.Modeling of bow wave effect in aerial refueling［C］//AIAA Atmospheric Flight Mechanics Conference.Toronto，Ontario Canada，2010.

［3］ Williamson W R，Reed E，Glenn G J，et al.Controllable drogue for automated aerial refueling［J］.Journal of Aircraft，2010，47(2):515-527.

［4］ 劉曌，周春華，袁鎖中.軟管式自主空中加油飛行控制系統與仿真研究［J］.系統仿真學報，2012，24(10):2054-2059.

［5］ Ellsworth J A，Fox W R，Lovendahl D E，et al.Guided drogue flight test report［R］.NAVY TRE-23027，1978.

［6］ 胡孟權，聶鑫，王麗明.插頭-錐管式空中加油軟管平衡拖曳位置的計算［J］.空軍工程大學學報，2009，10(5):22-26.

［7］ 王海濤，董新民，竇和鋒，等.軟管錐套式空中加油系統建模與特性分析［J］.北京航空航天大學學報，2014，40(1):92-98.

［8］ Kapseong Ro，Basaran E，Kamman J W.Aerodynamic characteristics of paradrogue assembly in an aerial refueling system［J］.Journal of Aircraft，2007，44(3):963-970.

［9］ 汪榮鑫.數理統計［M］.西安:西安交通大學出版社，1986:174-185.

［10］范奎武.用四元數描述飛行器姿態時的幾個基本問題［J］.航天控制，2012，30(4):49-53.