四階微分系統廣義主次譜之比的下界

黃振明

(蘇州市職業大學基礎部，江蘇蘇州215104)

考慮如下四階微分系統廣義譜的估計問題

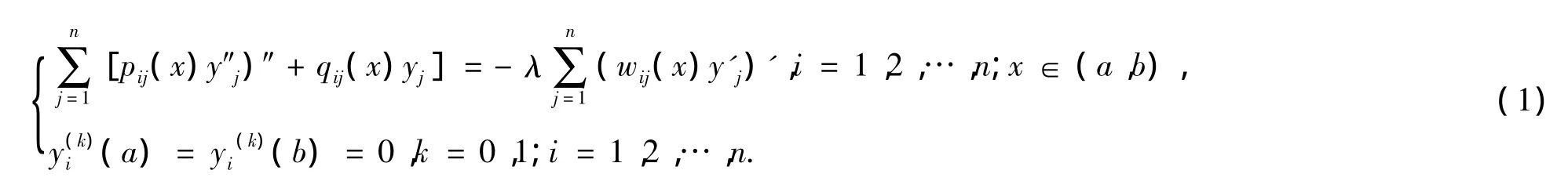
其中(a，b)R是一個有界開區間，pij(x)∈C2［a，b］，qij(x)∈C［a，b］，wij(x)∈C1［a，b］，且滿足pij(x)=pji(x)，qij(x)=qji(x)，wij(x)=wji(x)(i，j=1，2，…，n)，為方便推導，令

利用上述矩陣和向量記號，首先將微分系統(1)寫成如下等價的矩陣形式

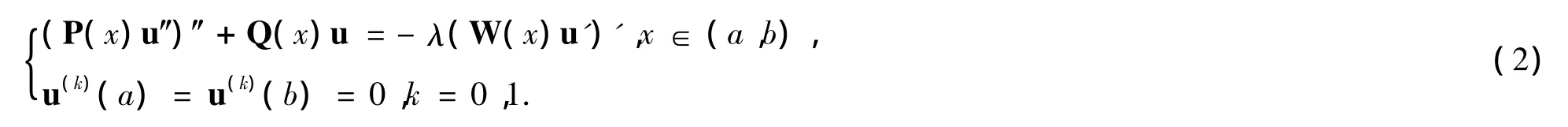
在推導定理的過程中還需用到如下條件:對任意n維向量ξ=(ξ1，ξ2，…，ξn)T有

上述μi，vi(i=1，2)均為正常數，T表示轉置.

微分方程的離散譜問題是微分方程譜理論領域一個重要的研究課題，自從法國數學家Sturm和Liouville提出了有關離散譜函數空間理論之后，譜問題受到了越來越多的關注，特別是近數十年來，許多數學工作者運用Sturm－Liouville理論，對實際問題中產生的單個微分方程(如梁橫向振動方程、重調和方程等)進行了譜估計，并取得了一系列成果，有關結論可查閱文獻［1－8］，但對于比較復雜的問題，為了更精確地描述它的自然現象，在歸結方程時，就必須考慮更多的因素和它們之間的相互作用，其數學模型一般需要用微分方程組來表示。例如，在一定條件下，諧振回路的數學模型就可用四階微分方程組來表示。為此，筆者討論上述由任意多個方程構成的方程組(2)的廣義譜估計，參照文獻［1］的討論方法，獲得了關于問題(2)的主次離散譜之比的下界估計不等式，且其估計系數與區間的幾何度量無關，文獻［2］討論的四階微分方程廣義譜問題僅是本文問題(2)當時的特例，因此問題(2)的廣義譜估計結果可視為文獻［2］結論的進一步推廣，在物理學和力學，特別是解決工程技術中的振動問題和穩定性問題時有著一定的參考價值［9－11］，同時，本文的工作對進一步討論高階常微分系統乃至偏微分系統的離散譜問題也有一定的啟迪作用，主要結果如下.

定理1 設λ1，λ2分別是問題(2)的主、次離散譜，且0＜λ1＜λ2，則有

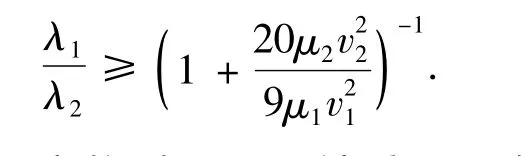
首先，說明問題(2)的離散譜λ都為正實數，在(2)兩端乘u，再在區間(a，b)上積分，利用(3)、(4)和分部積分公式，并利用邊界條件，可得

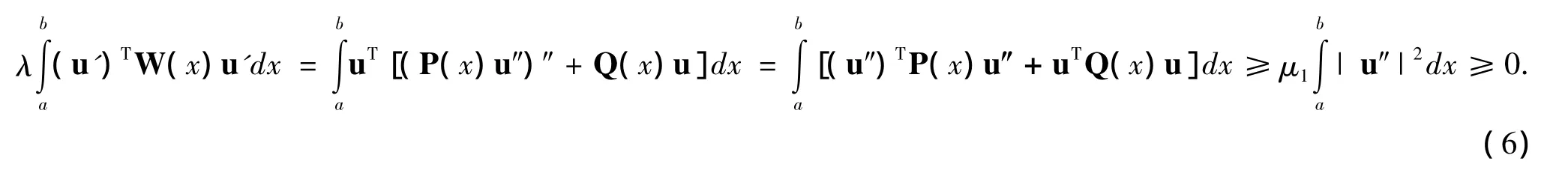
另外，由問題(2)中邊界條件和(5)，可得

由(6)和(7)可知，λ為非負實數.

另一方面，λ不會等于零，否則由(6)知，u″=0，可推得u=c1+c2x(其中c1，c2為任意n維常向量)，代入邊界條件u(a)=u'(a)=0，即得c1=c2=0，也即u≡0，而這與特征向量為非零向量矛盾，所以λ=0.

設問題(2)的主、次譜分別為λ1和λ2，由上面的討論知道，它們滿足0＜λ1≤λ2，記對應于λ1的特征向量為u，且滿足對上式分部積分得

利用(5)和(8)，得

由(6)和(8)，得

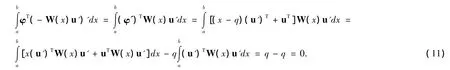
從(11)知，φ與u廣義正交，且滿足奇次邊界條件φ(k)(a)=φ(k)(b)=0(k=0，1)，由Rayleigh商的最小化性質可得

利用φ的定義和(2)，計算可得

φ″=(x－q)u″+2u'.

(P(x)φ″)″=(x－q)(P(x)u″)″+2(P(x)u″)'+2(P(x)u')″

(P(x)φ″)″+Q(x)φ =(x－q)［(P(x)u″)″+Q(x)u］+2(P(x)u″)'+2(P(x)u')″=－λ1(x－q)(W(x)u')'+2(P(x)u″)'+2(P(x)u')″.

上式兩端同乘φ并在［a，b］上積分可得

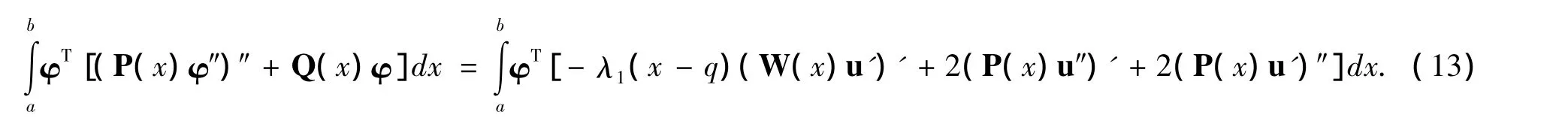
另一方面，利用分部積分和恒等式(x－q)u'=φ'－u，可得

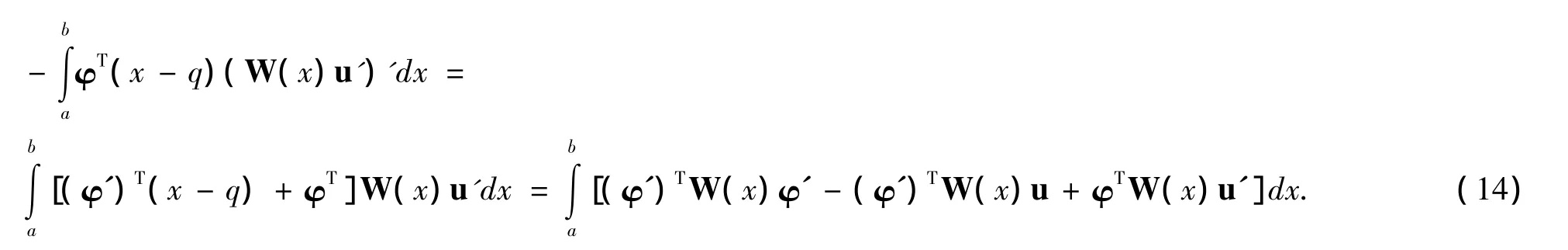
根據(13)和(14)，得

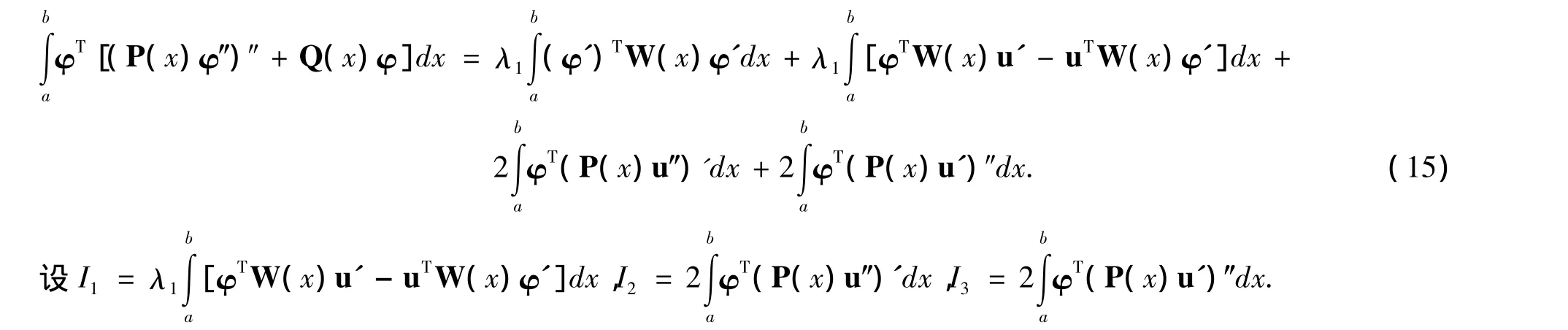
由(15)，得

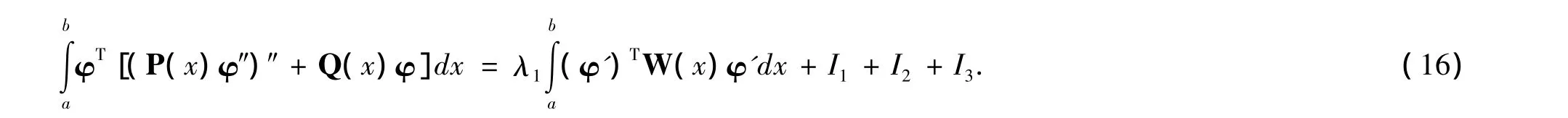
利用(12)和(16)，有

下面估計積分I1+I2+I3的上界和積分的下界.

引理1 設u是問題(2)對應于主譜λ1的特征向量，則

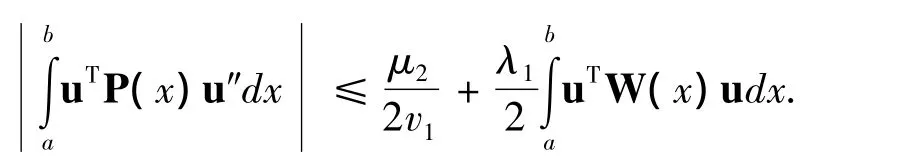
證明 利用式(3)、(5)、(6)、Cauchy－Schwartz不等式和基礎不等式有

表15和16給出了LAS及本文方法的迭代過程及設計點處可靠度值。表17給出了本文方法迭代點處的局部采樣半徑值。可以看出，相較于LAS方法，本文方法每次迭代所需的樣本點更少，最終求解也更為準確。

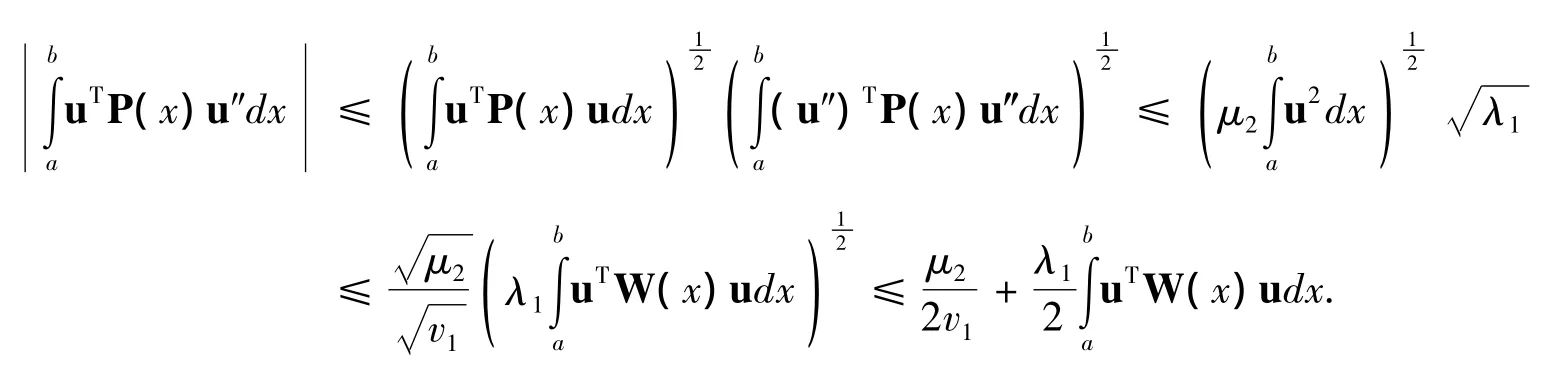
則引理1得證.

引理2 設λ1是問題(2)的主譜，則

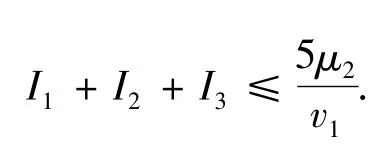
證明 利用分部積分和φ的定義，計算可得

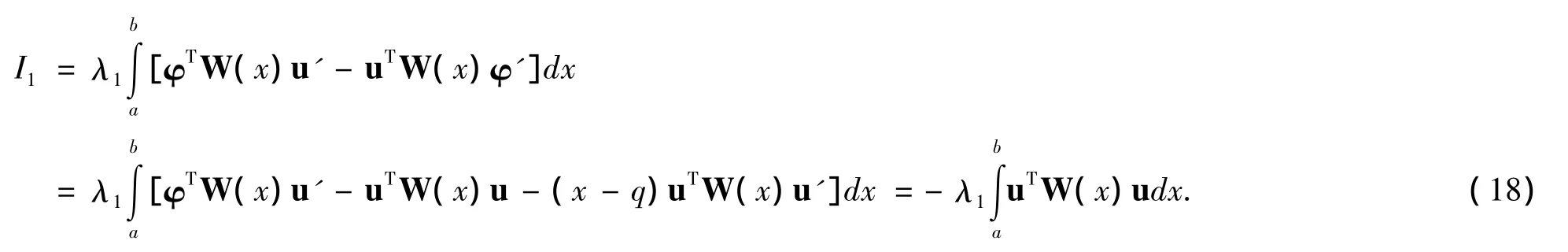
通過推算，類似可得

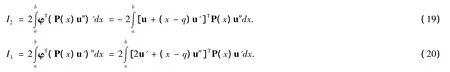
結合(18)、(19)和(20)，有

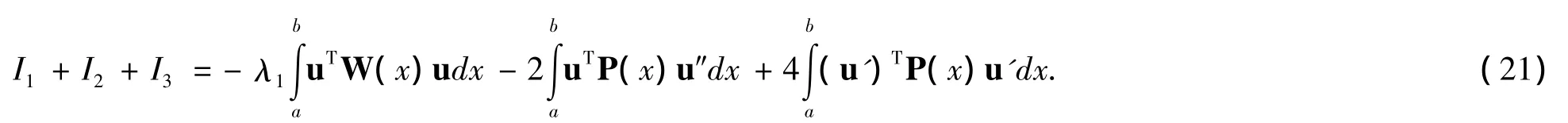
引理3 對于上述定義的φ與λ1，下列估計式成立

證明 利用分部積分和φ的定義，有

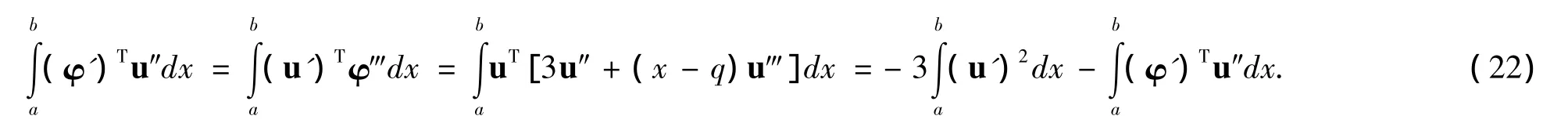
由(22)，可得恒等式

利用(5)、(9)、(10)、(23)和 Cauchy－ Schwartz不等式得

整理上式，即得引理3.

定理1的證明

將引理2的估計結論代入(17)得到

再將引理3的估計不等式代入(24)，經化簡整理即得定理1的結論.

注1 特別地，當微分系統(2)中P(x)、W(x)為數量矩陣時，有μ1=μ2，v1=v2，此時，由定理1可得到更簡潔的用主譜估計次譜上界的不等式

注2 至于微分系統(2)在其它邊界條件下是否有類似定理1的估計結論還有待于進一步研究.

［1］曾維國，錢椿林.斯圖姆－劉維爾問題的特征值［J］.工科數學，1992，8(1):28－32.

［2］黃振明.一類四階微分方程第二廣義譜的估計［J］.三明學院學報，2011，28(5):13－16.

［3］陳祖墀，錢椿林.任意階Laplace算子的離散譜估計［J］.中國科技大學學報，1990，20(3):259－265.

［4］賈高.梁橫向振動方程的特征值估計［J］.安徽大學學報，1997，21(2):29－33.

［5］金光宇，錢椿林.四階常微分方程的特征值估計［J］.蘇州絲綢工學院學報，1996，16(4):115－119.

［6］韓秋敏，錢椿林.六階某類微分方程第二特征值的上界［J］.蘇州大學學報，1999，15(4):26－30.

［7］盧亦平，錢椿林.微分方程帶一般權的第二特征值的上界估計［J］.長春大學學報:自然科學版，2009，19(10):7－10.

［8］Hile G N，Yeh R Z.Inequalities for Eigenvalues of the Biharmonic Operator［J］.Pacific J Math，1984，112(1):115 －132.

［9］Protter M H.Can one hear the shape of a drum［J］.SIAM Rev.1987，29(2):185 －197.

［10］Hook S M.Domain independent upper bounds for eigenvalues of elliptic operator［J］.Trans Amer Math Soc，1990(318):615－642.

［11］Mark S A.The universal eigenvalue bounds of Payne－Polya－Weinberger，Hile－Protter，and H C Yang［J］.Proc.Indian Acad.Sci.Math.Sci.，2002，112(1):3 －30.