完全圖的譜
李映輝 ,王守峰
(1.昆明學院數學系,云南昆明650224;2.北京大學數學學院,北京100871;3.云南師范大學數學學院,云南昆明650092)
圖譜理論是圖論研究的一個活躍而重要的領域,它在量子化學、統計力學、計算機科學、通訊網絡以及信息科學中均有著廣泛的應用.在圖譜論中,圖與多種矩陣自然地結合在一起,如鄰接矩陣、關聯矩陣、拉普拉斯矩陣、無符號拉普拉斯矩陣和距離矩陣等.完全圖是圖論中一類基礎而重要的圖,其結構的特殊性導致了它的研究方法的差異性及其結果的簡潔性.
本文首先介紹了完全圖Kn的鄰接矩陣、拉普拉斯矩陣、無符號拉普拉斯矩陣;然后通過組合數學和矩陣論的方法獲得了完全圖的特征多項式及其鄰接譜,即是包含圖論信息的代數結構;最后,研究了完全圖的特征多項式的系數與圖的結構之間的關系,證明了完全圖的鄰接譜、拉譜拉斯譜和無符號拉譜拉斯三者之間的關系.
1 基本概念
設圖Γ的頂點集VΓ是集合{v1,v2,…,vn},邊集EΓ作為頂點集VΓ的無序對的集合,如果{vi,vj}在邊集EΓ中,就稱vi與vj是鄰接的.完全圖Kn是一個有n個頂點且相異頂點均互相鄰接的圖.
定義1[1]圖Γ的鄰接矩陣是一個n×n矩陣A=A(Γ),它的元素滿足

從鄰接矩陣A的定義可直接得到其是一個實對稱陣,A的跡為trace(A).由于矩陣A的行和列對應圖Γ標記后的頂點,研究鄰接矩陣的性質就是研究行列置換后的不變量,即鄰接矩陣A的譜的性質.設變量λ是矩陣A的特征值,由于A是實對稱陣,故λ是實數,作為方程det(λI-A)=0的根λ的重數是對應λ的特征向量空間的維數.
定義2[1]鄰接矩陣A的特征多項式det(λΙ-A)稱為圖Γ的特征多項式,記為χ(Γ;λ),A=A(Γ)的特征值也稱為圖Γ的特征值.
定義3[1]圖Γ的鄰接譜是A(Γ)的特征值和它們各自重數的集合.若A(Γ)的特征值是λ0>λ1>…> λs-1,它們的重數分別是 m(λ0),m(λ1),…,m(λs-1),記 A(Γ)的鄰接譜為
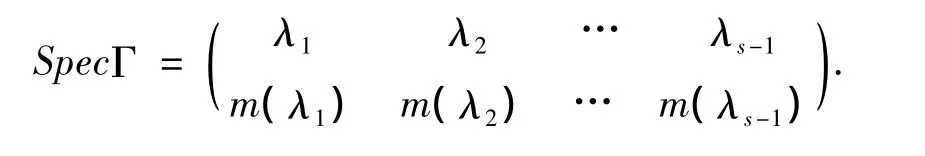
定義4[1]設A是一個矩陣,A的譜展是s(A)=maxij{|λi- λj|}.
其中max是指取遍鄰接矩陣A的所有特征值.
定義5[2]設Γ是一個沒有自環的無向圖.圖Γ的拉普拉斯矩陣L(Γ)的指標是圖Γ的頂點集,且行和為0.其中Lxy=-Axy,當x≠y.設D(Γ)是一個指標是圖Γ的頂點集,使得Dxy是頂點x的度,則拉普拉斯矩陣L(Γ)=D(Γ)- A(Γ),Q(Γ)=D(Γ)+A(Γ)就是無符號矩陣.
在連通圖Γ中,連接vi和vj的路徑的最少邊數稱作vi與vj的距離,記作(vi,vj).連通圖Γ中距離函數的最大值稱作圖Γ的直徑.
2 預備結論
設圖 Γ 的特征多項式是 χ(Γ;λ)= λn+c1λn-1+c2λn-2+c3λn-3+ … +cn,在此公式中-c1是0,即特征值的和,由于A的跡trace(A),因此c1=0.
引理1[1]圖Γ的特征多項式的系數滿足:(1)c1=0;(2)-c2是圖Γ的邊數;(3)-c3是圖Γ中三角形數目的兩倍.
命題1 圖Γ的特征多項式的系數cn具有性質cn=(-1)n|A|.
證明 因為圖Γ的特征多項式是χ(Γ;λ)=det|λI-A|,當其變量λ =0,
cn= χ(Γ;λ)=det(λI- A)=|- A|=(- 1)n|A|.
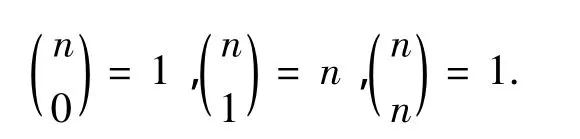
引理2[3]若0≤ r≤n,則
引理3[3]對于所有的整數n和k滿足1≤k≤n-1,則
命題2 對于所有的整數n和k滿足1≤k≤n-1,則(k-1
證明 根據引理2和引理3,有
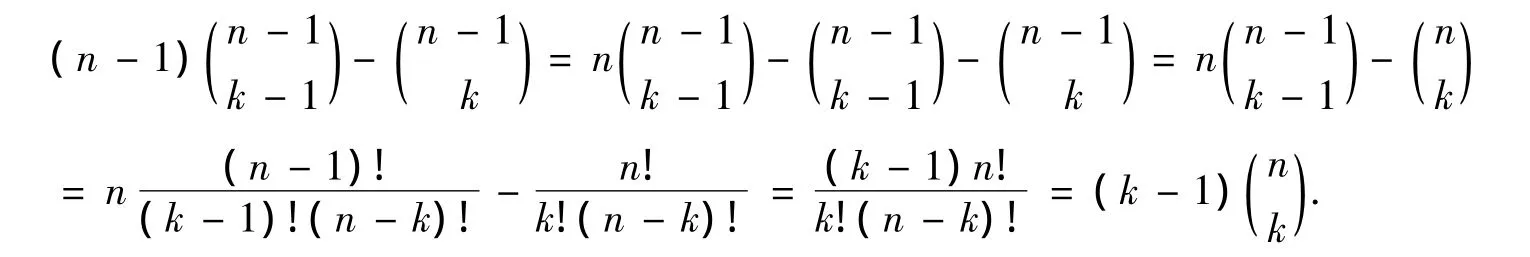
完全圖Kn是一個有n個頂點且相異頂點均互相鄰接的圖,所以自然有完全圖Kn的鄰接矩陣是
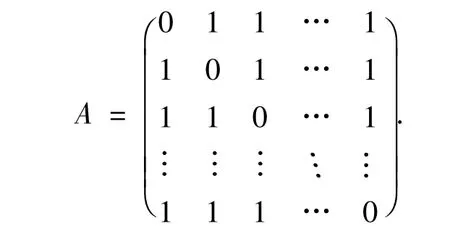
命題3 完全圖Kn的特征多項式是 χ(Kn,λ)=(λ -n+1)(λ +1)n-1.
證明

=(λ-n+1)(λ +1)n-1.
由于完全圖Kn是k-正則圖,即每一個頂點有相同的度k=n-1,根據拉普拉斯矩陣的定義,有完全圖Kn的拉普拉斯矩陣
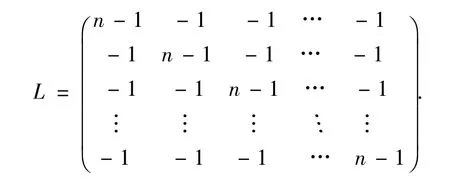
類似完全圖Kn的特征多項式,可得到如下命題.
命題4 完全圖Kn的拉普拉斯矩陣L的特征多項式是Chapo(L,θ)=θ(θ-n)n-1.
同樣的方法可以得到完全圖Kn的無符號拉普拉斯矩陣Q,
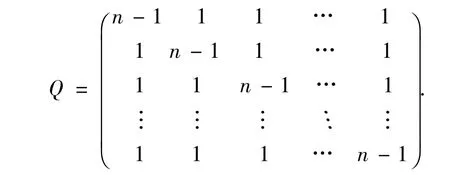
命題5 完全圖Kn的無符號拉普拉斯矩陣的特征多項式是
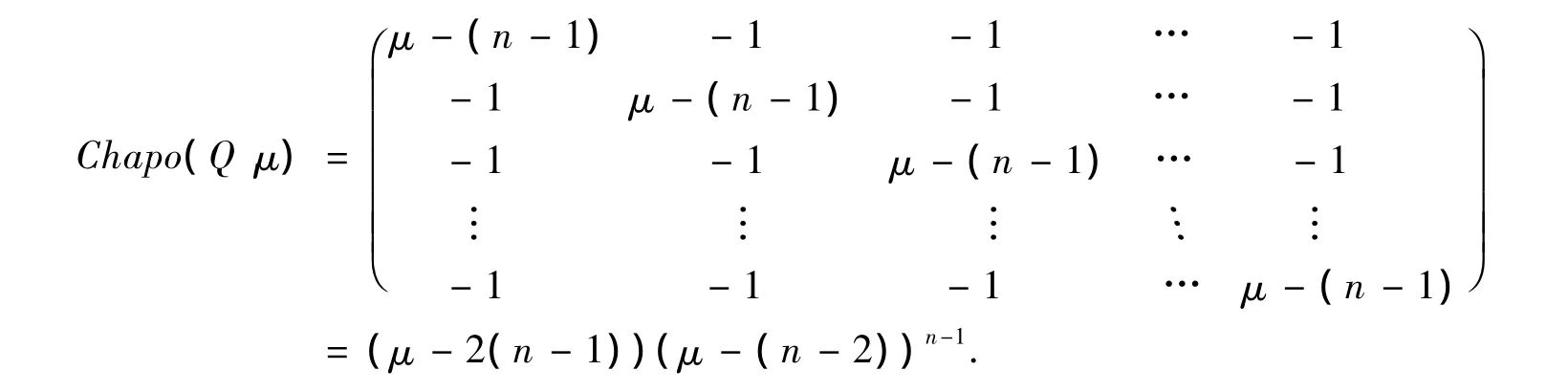
3 主要結果
命題 6 完全圖 Kn的特征多項式具有形式 χ(Γ;λ)= λn+c1λn-1+c2λn-2+c3λn-3+ … +cn,其中 ck=
證明 在命題3中給出了完全圖的Kn特征多項式,根據命題2有
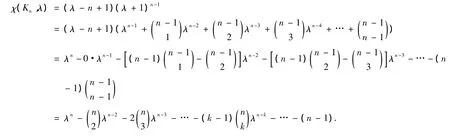
由于完全圖有其自身的特殊結構和性質,即每一對相異頂點都是鄰接的.根據引理1可知是Kn的邊的數目是圖Γ中三角形的數目.對于有向圖而言是Kn中三角形數目的2倍.另一方面,在命題2中已經有完全圖Kn的鄰接矩陣的系數的性質,即c1=trace(A)=a11+a22+…+ann=0.當它的變量λ=0時,有cn= χ(Γ;λ)=det(λI-A)=|-A|=-(n-1).
定理1 完全圖Kn的特征多項式的系數滿足下列性質:(1)c1=0;(2)是Kn中邊的數目;(3)是Kn中三角形數目的2倍;(4)-cn=n-1.
在命題3中,完全圖Kn的特征值是λ0=n-1,λ1=λ2=… =λn-1=-1,或者說特征值為 -1的重數是n-1.
定理2 完全圖Kn的譜是
在矩陣論中已經證明了鄰接矩陣的特征多項式的系數c1是A的跡trace(A),它的所有特征值之和c1=λ0+λ1+… +λn-1=(n-1)-(n-1)=0;特征多項式的系數 cn是所有特征值之積 cn= λ0λ1…λn-1=(- 1)n-1(n-1).
顯然完全圖是連通圖,所以Kn的直徑是1.
引理4[1]設連通圖Γ的鄰接代數是δ(Γ),半徑是d,那么鄰接代數δ(Γ)的維數至少是d+1.
推論 完全圖Kn的鄰接代數δ(Γ)的維數至少是2,并且有2個不同的特征值.
定理3 完全圖Kn的譜展是n.
證明 由于譜展是s(A)=maxij{ λi- λj},所以
s(A)=maxij{ λi- λj}=|λ0- λ1|=|(n-1)-(-1)|=n.
綜合命題3、命題4和命題5,完全圖Kn的鄰接譜、拉普拉斯譜、無符號拉普拉斯譜分別為
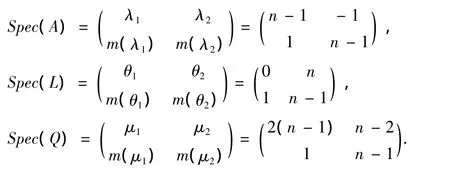
由定理2和以上研究,可得到如下性質.
定理 4 μ1=2λ1=2k,μ2=2λ2+ θ2.
[1]Norman Biggs.Algebraic Graph Theory[M].Second Edition.London:Cambridge University Press,1993.
[2]Andries E.,Brouwer and Willem H.Haemers.Spectra of Graphs[M].London:Springer,2012.
[3]Richard Brualdi.Introductory Combinatorics[M].Fifth Edition.Beijing:China Machine Press,2012.
[4]D.Cvetkovic,S.Simmic.Graph Spectra in Computer Science[J].Linear Algebra and its Applications,2011(434):1545-1562.

