新非平穩信號分析方法-自適應徑向墨西哥草帽核時頻分布

第一作者李志農男，博士，教授，1966年8月生

新非平穩信號分析方法—自適應徑向墨西哥草帽核時頻分布

李志農，朱明，龍盛蓉(南昌航空大學無損檢測技術教育部重點實驗室, 南昌330063)

摘要：據自適應最優核設計準則，構造新的自適應徑向墨西哥草帽型核函數時頻分析方法。該方法能據分析信號分布自適應調節核函數的擴展方向及寬度，使在信號自項方向盡可能延伸，而不在信號自項方向的互項盡可能抑制，能克服傳統時頻分布中固定核函數缺乏對信號自適應能力的不足。給出自適應徑向墨西哥草帽型核函數時頻分布定義及算法，并與傳統的短時傅里葉變換、Wigner-Ville分布及小波變換方法對比分析。仿真結果表明，所提方法優于傳統的時頻分布方法，能更有效處理非平穩信號，可獲得較傳統時頻分布分辨率及抗噪更高性能。通過用于轉子裂紋故障診斷實驗結果表明，該方法能有效反映裂紋故障的嚴重程度。

關鍵詞：徑向墨西哥草帽核；自適應時頻分布；自適應優化；故障診斷；裂紋轉子

基金項目：國家自然科學基金(51075372，50775208， 51265039);江西省教育廳科技計劃項目(GJJ12405);湖南科技大學機械設備健康維護湖南省重點實驗室開放基金(201204) ;江西省研究生創新基金項目(YC2013-S214)

收稿日期：2014-02-08修改稿收到日期：2014-05-23

中圖分類號:TN911;TH165.3;TH17;TP391文獻標志碼：A

A new method for non-stationary signal analysis-adaptive radial mexican-hat kernel time-frequency distribution

LIZhi-nong,ZHUMing,LONGSheng-rong(MOE Key Laboratory of Nondestructive Testing, Nanchang Aeronautical University, Nanchang 330063, China)

Abstract:A new adaptive radial Mexican-hat kernel (RMK) time-frequency distribution method was proposed according to the design criteria of adaptive optimal kernel. The characteristic of the proposed method was that RMK could self-adaptively adjust the expansion direction and width of the kernel function according to the distribution of the analyzed signal. The kernel function expanded as far as possible in auto-term direction, and was suppressed as far as possible in cross-term direction to overcome the deficiency of lack of self-adaptability for the fixed kernel function in the traditional time-frequency distribution. Here, the definition and the algorithm of RMK were presented, and the proposed method was compared with the traditional time-frequency distribution, such as, short Fourier transformation, Wigner-Ville distribution and wavelet transformation. The simulation results showed that the proposed method is superior to the traditional time-frequency distribution, it can more effectively be used to process non-stationary signals, and obtain the higher time-frequency resolution and anti-interference performance. Finally, the proposed method was applied in the fault diagnosis of rotor crack. The test results showed that the proposed method is very effective and can reflect the severity of rotor crack fault.

Key words:radial mexican-hat kernel; adaptive time-frequency distribution; adaptive optimization; fault diagnosis; cracked rotor

工程中所得動態信號往往具有非平穩性。由于非平穩動態信號的統計特性與時間有關，故對其須同時進行時、頻分析[1]。時頻分析能提供頻譜內容隨時間變化的信息，為非平穩信號分析的有力工具[2]。然而，傳統的短時傅里葉變換、小波變換、Cohen類雙線性時頻分布等分析方法均采用固定的核函數，對信號缺乏自適應性，導致分析結果往往失去實際物理意義而不能正確提取信號本質特征[3-4]。Baraniuk等[5-6]針對雙線性時頻分布中核函數固定不變、對信號缺乏自適應缺點，提出自適應優化核函數的設計準則，大大增強對非平穩信號的處理能力，可據不同類型信號進行自適應處理[7-11]。本文針對固定核缺陷，據自適應優化核設計準則，提出新的自適應墨西哥草帽核時頻分布。該方法能隨信號模糊函數不同而自適應調節核的方向，使之與模糊函數的自項相匹配且最大限度擴展自項方向核函數，對其它方向進行最大抑制，自項獲得最大保留，交叉項得到較好抑制，時頻分辨率高，亦能較好抑制噪聲。將該方法與傳統時頻分析方法在時頻分辨率及抑制噪聲能力方面進行對比分析，并用于裂紋轉子故障特征分析，實驗結果驗證該方法的有效性。

1自適應徑向墨西哥草帽核時頻分布構造

由于直角坐標系中傳統二次型時頻分布的核函數Φ(θ,τ)固定不變，不能隨信號不同而改變，對信號缺乏自適應性。為此，本文據自適應最優核設計準則，構造出二維徑向非增低通的墨西哥草帽(Mexican-hat)核函數，其極坐標形式為

(1)

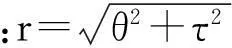
該核函數為徑向非增低通函數，隨遠離原點而光滑下降，引入參數ξ使核函數通帶與阻帶之前的寬度可調；亦可據模糊域中信號的自項方向，自適應調節核方向與自項方向匹配，盡可能使核在自項方向擴展,其它方向盡量收縮，使信號自項獲得最大的保留，交叉項得到最大抑制；且能較好抑制噪聲。

由式(1)可知，二維徑向函數是一維擴展函數的參數化表示，可將二維函數的優化求解問題轉換成一維函數的優化求解問題，優化目的簡化為尋找最優的一維擴展函數σ(ψ)。徑向Mexican-hat核函數的優化設計準則在極坐標形式下可表示為

(2)

約束條件為

(3)

(4)

式中：AF(r,ψ)為信號模糊函數極坐標形式。

式(3)將核函數限制為徑向Mexican-hat函數形式，式(4)中a限制核函數的能量體積，且直接影響自項的聚集程度及交叉項的抑制程度。因模糊函數關于原點對稱，式(3)中σ(ψ)積分范圍可變為0≤ψ≤π，故對式(4)化簡為

(5)

通過符號積分可得

(6)

式中：

η=[2+ξ2-2ξ-2exp(-ξ)]ξ-3

(7)

所以

(8)

對自適應最優Mexican-hat核函數的求解轉變為優化求解問題，即

(9)

約束為式(4)、式(8)。由式(9)可知，要實現最大化，模糊函數AF(r,ψ)越大，核函數Φ(θ,τ)越大。然而受a限制，其核函數能量體積有限。為實現極大化優化準則，核函數Φ(θ,τ)將盡可能對靠近模糊域原點的自分量方向作遠的擴展而對遠離模糊域原點的互分量方向盡可能收縮。參數a通過控制最優核體積決定交叉項抑制程度及自分量聚集程度。文獻[3-4]給出a的選擇原則，即通常情況下取1≤a≤5。a越小對互分量抑制越厲害，但會濾掉一些自分量，使分辨率降低；a越大時頻分辨率越高，但互分量則得不到較好抑制。因此，利用該方法需折中選擇。經多次試驗，本文認為選a=2最合適。

在所提出算法中需考慮調節系數ω，ξ的選擇。由式(3)知，ω及ξ值對Φ有直接影響，但整個優化選擇中a控制著核函數的能量體積，優化時σ2(ψ)初值為式(8)取等號情況。a不變時σ2(ψ)與ω成正比，故其結果對Φ影響不大。而隨ξ增大核函數過渡帶變小，形狀亦會發生一定變化，對時頻分辨率有一定影響。經大量試驗對比證明，ω對時頻分布影響不大，本文取ω=0.1。對ξ選擇，取ξ=1時能獲得較好結果。

自適應Mexican-hat核函數參數確定后，須進行約束條件下優化問題求解。工程應用中時頻分布計算總建立在離散化基礎上，因此須對優化目標函數及約束條件離散化。通常，模糊函數計算及從模糊域到時頻域轉換均在直角坐標系中進行，可利用快速傅里葉變換實現。而優化問題在極坐標中計算則更簡便。因此計算過程中涉及兩個坐標系的尺度變換。自適應徑向Mexican-hat核時頻分布計算步驟如下：

(1)對直角坐標系下信號的模糊函數AF(θ,τ)進行矩形采樣。設采樣長度為L，采樣間隔為T，則離散模糊函數為

AFd(m,n)=AF(θ;τ)|θ=mΔθ,τ=mΔτ

(10)

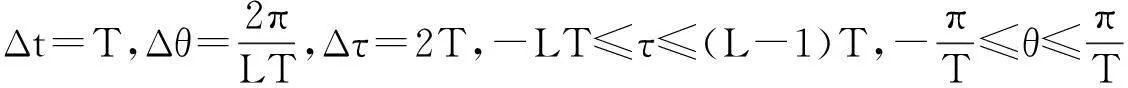
離散模糊函數表達式為

AFd(m,n)=

(11)

(2)直角坐標系下不便于信號的模糊函數優化，可通過插值轉化到極坐標下。為便于變換，設L×L矩形網格寬高比相等，對兩坐標系進行尺度轉換，令Δτ=Δθ，則

(12)

(13)

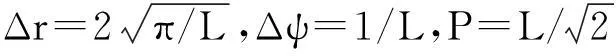
r=pΔr,(p=0,1,…,P-1)

ψ=qΔψ,(q=0,1,…,Q-1)

式中：p，q分別為極半徑、極角的采樣點。

獲得離散化模糊函數極坐標形式AFp(p,q)，此時核函數可表示為

(14)

(3)由上兩步得待優化目標函數及約束離散形式

(15)

(16)

由于最優核函數優化過程為非線性過程，直接求解計算量非常大，故采用梯度上升迭代算法求其最優解σq，令

(17)

迭代式為

σ(k+1)=σ(k)+μ(k)f(k)

(18)

(19)

(20)

為使算法收斂，用歸一化方法使約束條件成立，即

(4)將優化的最優核函數σq用插值法轉換到直角坐標系中。

(5)在直角坐標系中對模糊函數及最優核函數的乘積進行一次FFT及IFFT，即得最優時頻分布。

2性能研究

為驗證自適應徑向墨西哥草帽核時頻分布的有效性，構造仿真信號為

(22)

該信號由兩個復線性調頻信號之和構成，選采樣頻率fs=100 Hz，采樣點數N=256。其時域波形見圖1(a)，自適應徑向墨西哥草帽核時頻分布見圖1(b)。為對比分析，給出傳統的時頻分析方法所得Wigner-Ville分布、小波變換及短時傅里葉變換的時頻分布，見圖1(c)、(d)、(e)。從時頻分辨率及抗噪能力兩方面考察自適應徑向墨西哥草帽核時頻分布處理非平穩信號能力。

2.1時頻分辨率分析

對比圖1各時頻分布結果可知，對線性調頻信號，自適應墨西哥草帽核時頻分辨率明顯高于小波變換及短時傅里葉變換。Wigner-Ville分布雖分辨率最高，但存在嚴重的交叉干擾項，而自適應墨西哥草帽核時頻分布、小波變換及短時傅里葉變換均不存在交叉項。因此由時頻分辨率及交叉項抑制來看，自適應徑向墨西哥草帽核時頻分布明顯優于其它時頻分析方法。此可從理論上對該結果給出充分解釋。

短時傅里葉變換由于受Heisenberg測不準原的約束，時間、頻率分辨率不可能同時達到最佳，且其時頻窗口大小固定不變，缺乏自適應性。Wigner-Ville 時頻分布在模糊域中全通，時頻聚集性好，能較好反映信號的時頻特征，但存在遠大于自項的交叉干擾項，且其時頻分布仍采用固定核函數。即適合于某種特定類型信號分析的固定核函數不一定適合其它類型信號分析。況且Wigner-Ville 時頻分布缺乏對信號的自適應能力。小波雖具有可調時頻聚窗口，但存在一定局限，如小波基函數選擇對非平穩信號處理影響較大。故選合適的小波基滿足不同類型信號較困難[12-13]，往往只適用某些類型信號，而對其它類型信號不一定適用，對信號缺乏廣泛地自適應性。且小波變換的時移、頻移是固定變化的，只是對時頻平面進行機械的格型分割，因此在小波變換中小波基一經選擇，在整個分解、重構過程中均無法更改；小波基可能在全局上是最佳的，但對某個局部可能最差，故小波變換不具備自適應的信號分解特性。

與傳統短時傅里葉變換、Wigner-Ville分布、小波變換相比，自適應墨西哥草帽核時頻分布能據不同信號模糊函數自適應調節核的擴展方向及寬度，對在信號自項方向盡可能延伸，而對不在信號自項方向的互項盡可能抑制。因此該時頻分布自適應性較強。

圖1(f)為信號x(t)對應的自適應Mexican-hat核等高圖，可見Mexican-hat核能自動隨信號方向擴展，而在其它方向收縮，從而能得到最佳的時頻分辨率。

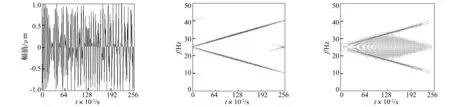
(a) 信號x(t)的時域波形　　　　　　(b)自適應徑向墨西哥草帽核分布　　　　　　　(c) Wigner-Ville分布

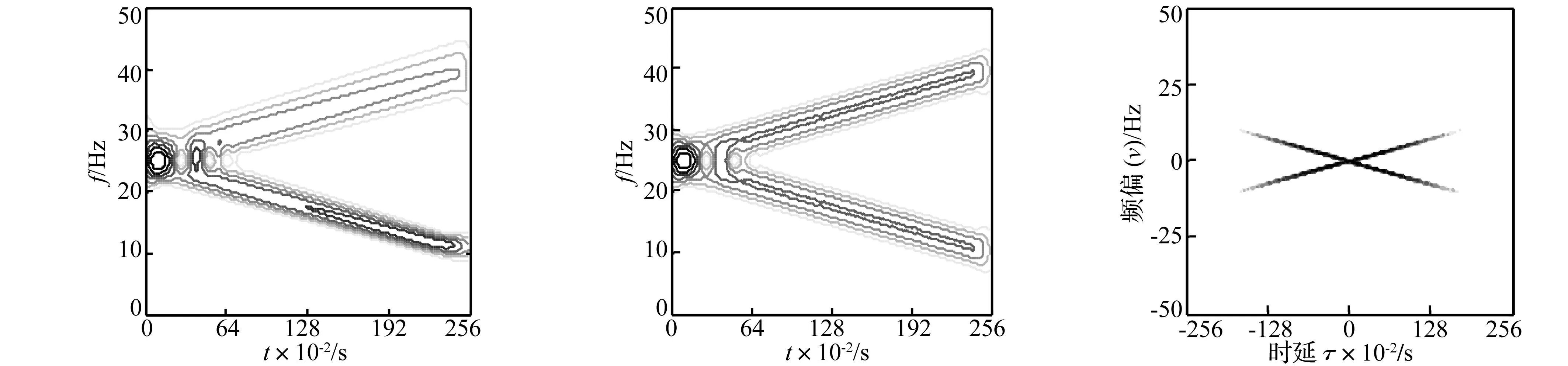
(d) 小波變換　　　　　　　　　　(e) 短時傅里葉變換　　　　　　　　(f) 信號x(t)對應的墨西哥草帽核 圖1　信號的時頻分布 Fig.1 The time-frequency distribution of signal

2.2抗噪性分析

自適應徑向墨西哥草帽核在二維平面上為低通核，而低通核有助于減少噪聲敏感度。為驗證該草帽核抑制噪聲的能力，對信號x(t)分別施加不同信噪比(SNR) 的高斯白噪聲進行測試。

分別加入信噪比5 dB、-1 dB的加性高斯白噪聲時自適應徑向墨西哥草帽核時頻分布見圖2、圖3。為對比分析，亦給出相應的不同噪聲環境下傳統Wigner-Ville分布、小波變換及短時傅里葉變換時頻分布。由圖2、圖3可知，Wigner-Ville分布存在嚴重的噪聲污染，信號特征完全被淹沒，此因信號在模糊域全通；小波變換及短時傅里葉變換時頻圖均存在不同程度的噪聲污染，不能較好分辨信號的時頻特征，且隨噪聲增強，反映信號的時頻特征越模糊。原因為兩種變換采用的固定小波函數、窗函數所致，缺乏自適應性。而自適應墨西哥草帽核時頻分布(圖2(b)、3(b))可清晰看出頻率隨時間線性變化特性，且絕大部分噪聲被抑制。明顯優于其它時頻分布，尤其信噪比越低該優勢越明顯。其原因為該自適應核在二維平面上為低通核，且能隨信號特征朝信號自項方向自動作盡可能延伸，在其它方向盡可能收縮，故噪聲能被盡可能抑制。

從時頻分辨率及抗噪能力兩方面均明顯反映出自適應墨西哥草帽核時頻分布在處理非平穩信號方面優于Wigner-Ville分布、小波變換、短時傅里葉變換。該草帽核時頻分布為優秀的自適應時頻分析方法。

3實驗研究

為進一步驗證方法的有效性，利用自適應徑向墨西哥草帽核時頻分布對轉子裂紋故障進行分析。實驗在Bently轉子試驗臺上進行，為分析不同裂紋的自適應徑向墨西哥草帽核時頻分布特性，加工兩根裂紋深度不同的軸，一根裂紋深度為直徑的25%，另一根為直

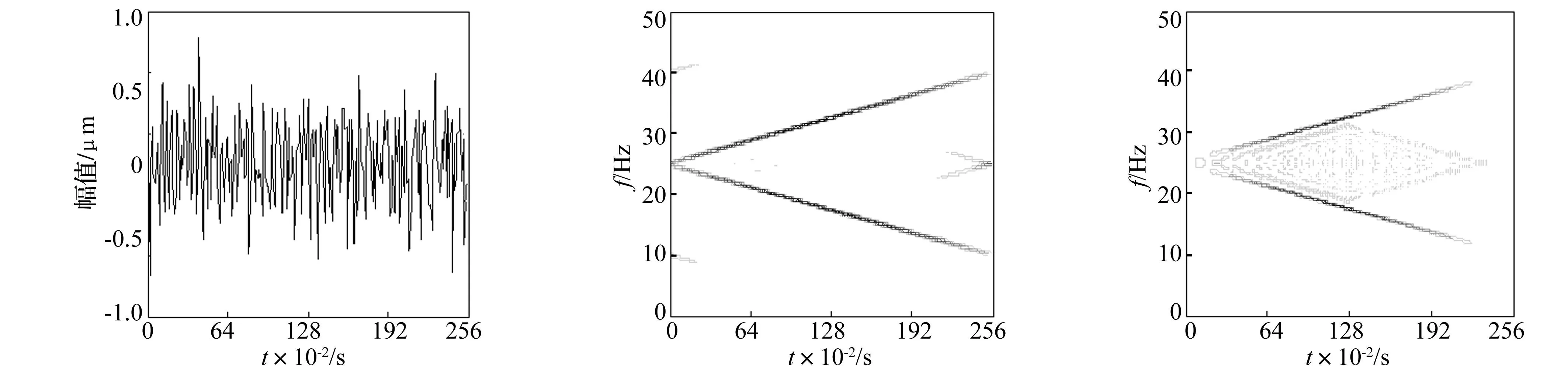
(a) 信號x(t)染噪后的時域波形,信噪比為5dB(b) 自適應徑向墨西哥草帽核分布(c) Wigner-Ville分布

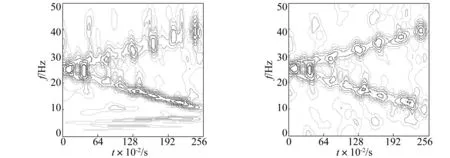
(d) 小波變換(e) 短時傅里葉變換圖2 各種時頻分布Fig.2Thetime-frequencydistribution

(a) 信號x(t)染噪后的時域波形,信噪比為-1dB(b) 自適應徑向墨西哥草帽核分布(c) Wigner-Ville分布

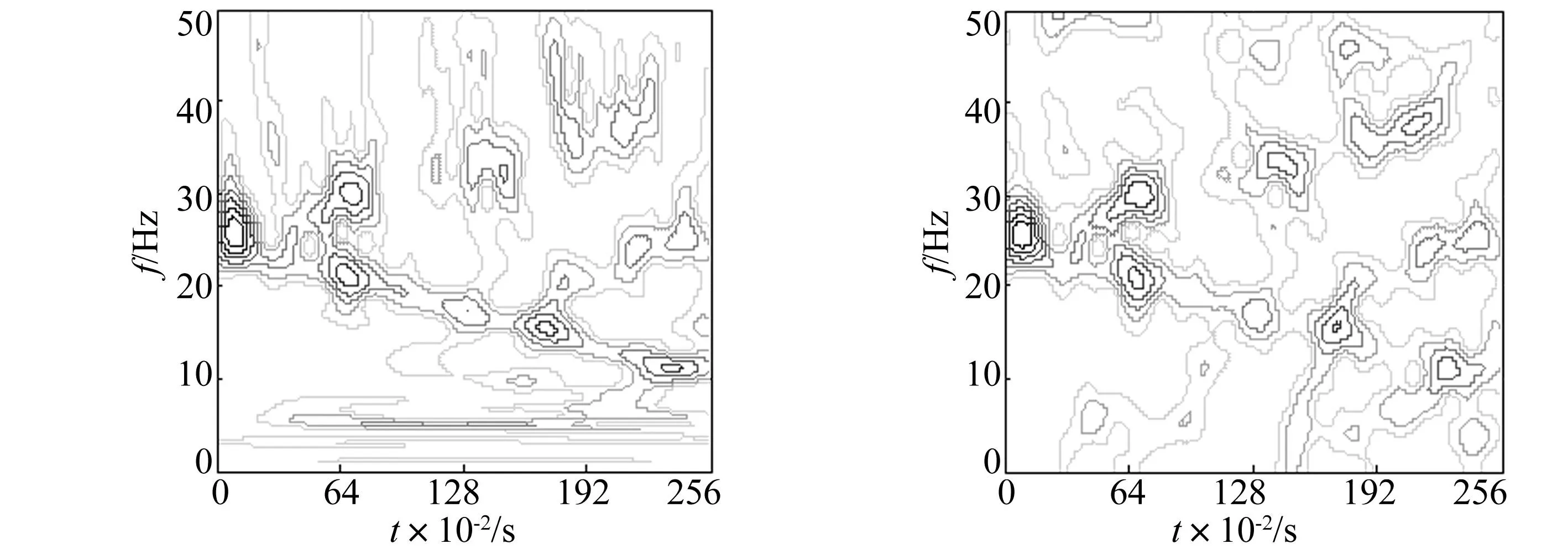
(d) 連續小波變換分布(e) 短時傅里葉變換分布圖3 各種時頻分布Fig.3Thetime-frequencydistribution

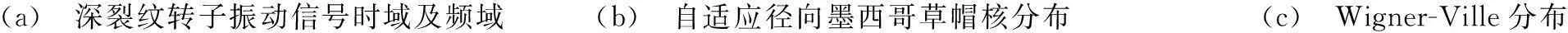
(a) 深裂紋轉子振動信號時域及頻域(b) 自適應徑向墨西哥草帽核分布(c) Wigner-Ville分布

(d) 小波變換(e) 短時傅里葉變換圖4 淺裂紋的時頻分布Fig.4Thetime-frequencyofshallowcrack

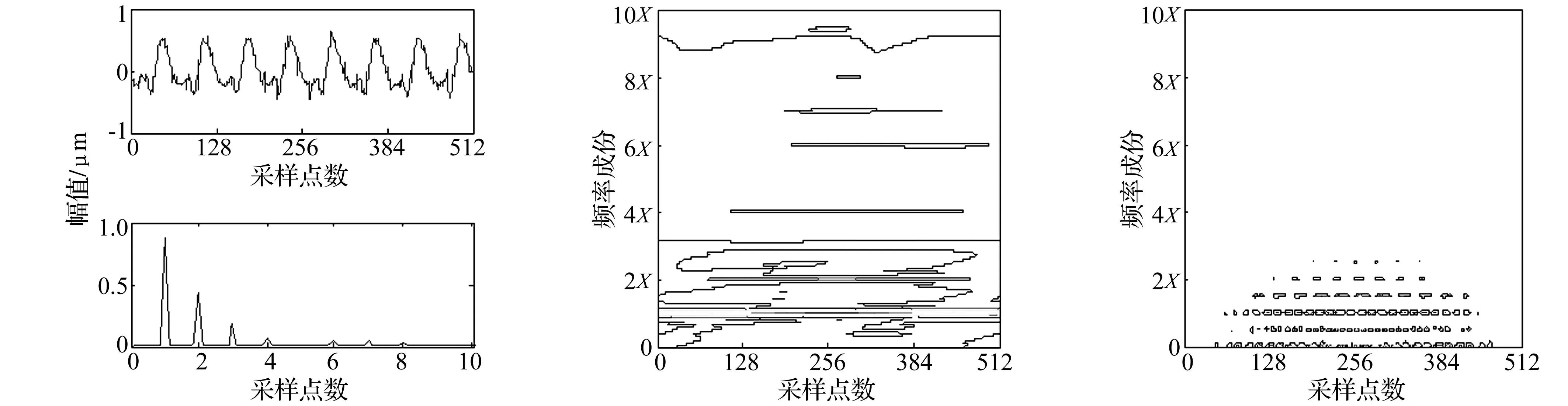
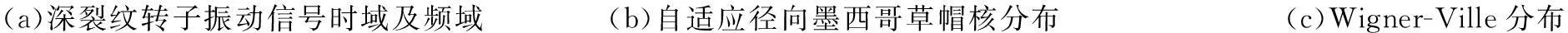
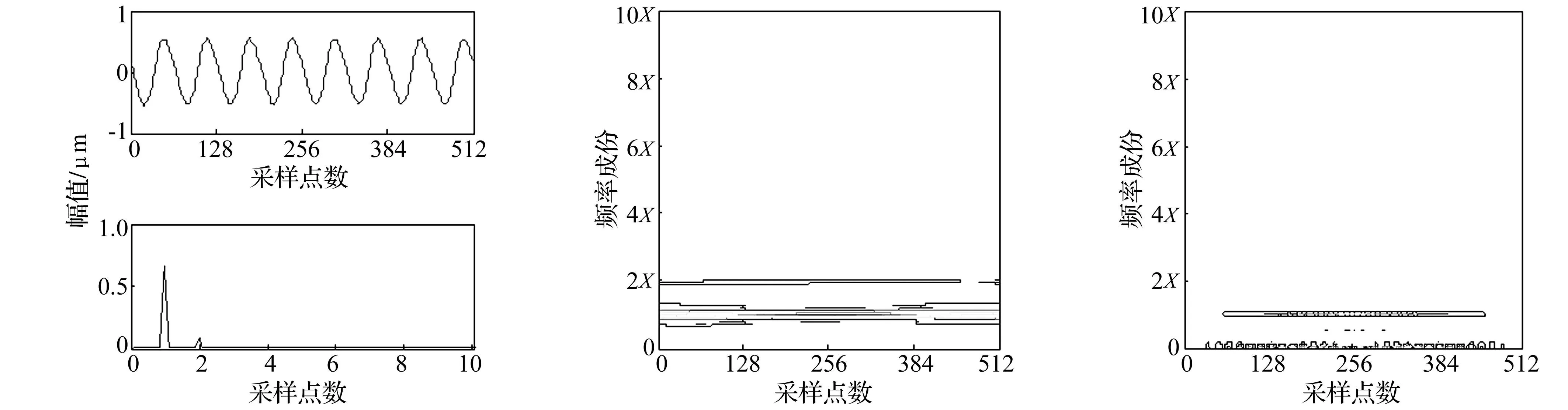
(a)深裂紋轉子振動信號時域及頻域(b)自適應徑向墨西哥草帽核分布(c)Wigner-Ville分布

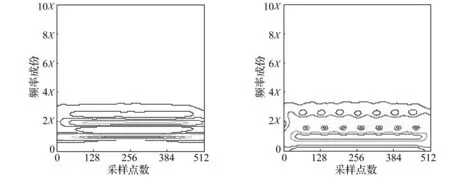
(d)小波變換(e)短時傅里葉變換圖5 深裂紋的時頻分布Fig.5Thetime-frequencyofdeepcrack

徑的50%。裂紋軸加工方法為：用線切割機在軸上指定位置切割出給定深度槽，切槽寬度約0.12 mm；在切槽中嵌入厚度0.10 mm金屬片，形成近似開閉裂紋。為防止薄金屬片實驗中脫落，嵌入切槽前在薄金屬片某面涂502膠水與切槽粘牢[14-15]。兩條不同程度裂紋轉子振動信號的時域圖、頻譜圖、自適應徑向墨西哥草帽核時頻分布及傳統的Wigner-Ville分布、小波變換、短時傅里葉變換時頻分布分別見圖4、圖5。其中圖4(a)、圖5(a)為不同裂紋深度時的時域圖、頻域圖，可知，頻譜中能看出倍頻信息，但卻看不出信號頻率隨時間變化特征。由圖4(b)、圖5(b)看出，淺裂紋時轉子系統自適應徑向墨西哥草帽核時頻分布的一、二倍頻占主要成分且持續存在，而隨裂紋深度增加，裂紋轉子系統除一、二倍頻等主要成分仍持續存在外，四、六、八倍等高倍頻成分相繼出現，較一、二倍頻弱，且只在一定時區內存在，與理論分析結果吻合。由圖4(c)、圖5(c)知，Wigner-Ville分布雖時頻分辨率高但存在嚴重的交叉干擾項，難以看清時頻特征。由圖4(d)、5(d),4(e)、5(e)知，小波變換及短時傅里葉變換的時頻分辨率均不及本文時頻分布方法。因此，自適應徑向墨西哥草帽核時頻分布能有效反映裂紋故障的嚴重程度。

4結論

針對傳統時頻分布中固定核函數缺乏對信號的自適應能力的不足，據自適應最優核設計準則，提出新的自適應墨西哥草帽核時頻分布。給出該核函數的定義、優化方法及算法，考察該方法對非平穩信號處理能力，并與傳統的Wigner-Ville分布、小波變換、短時傅里葉變換進行對比分析,結論如下：

(1)所提時頻分布無論對時頻分辨率或噪聲抑制均優于傳統的時頻分析方法，因核函數為二維的徑向非增低通核函數，且能隨信號特征朝信號自項方向自動盡可能延伸，在其它方向盡可能收縮，交叉項及噪聲被盡可能抑制。

(2)通過進行轉子裂紋故障診斷實驗，結果進一步驗證所提方法的有效性。

參考文獻

[1]何正嘉,訾艷陽,孟慶豐,等. 機械設備非平穩信號的故障診斷原理及應用[M].北京: 高等教育出版社, 2001.

[2]向玲,唐貴基,胡愛軍. 旋轉機械非平穩振動信號的時頻分析比較[J]. 振動與沖擊, 2010,29(2): 42-45.

XIANG Ling,TANG Gui-ji, HU Ai-jun. Vibration signal’s time-frequency analysis and comparison for a rotating machinery[J]. Journal of Vibration and Shock, 2010,29(2): 42-45.玲,唐貴基,胡愛軍. 旋轉機械非平穩振動信號的時頻分析比較[J]. 振動與沖擊, 2010,29(2): 42-45.

XIANG Ling,TANG Gui-ji, HU Ai-jun. Vibration signal’s time-frequency analysis and comparison for a rotating machinery[J]. Journal of Vibration and Shock, 2010,29(2): 42-45.

[3]Sheng Chen-xing, Li Zhi-xiong, Li Qin, et al. Recent progress on mechanical condition monitoring and fault diagnosis[J]. Procedia Engineering, 2011,15: 142-146.

[4]Zhao X M, Patel T H, Zuo M J. Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J]. Mechanical Systems and Signal Processing,2012,27:712-728.

[5]Baraniuk R G,Jones D L. A signal dependent time-frequency representation: optimal kernel design[J]. IEEE Trans on Signal Processing, 1993, 41(4) :1959-1602.

[6]Baraniuk R G, Jones D L. Signal dependent time-frequency analysis using a radially Gaussian kernel[J].Signal Processing, 1993, 32(3) : 263-284.

[7]Alp Y K, Arikan O. Time-frequency analysis of signals using support adaptive Hermite-Gaussian expansions[J]. Digital Signal Processing, 2012,22:1010-1023.

[8]Jones D L, Baraniuk R G. An adaptive optimal-kernel time-frequency representation[J].IEEE Trans. on Signal Processing,1995,43(10):2361-2371.

[9]Zhao Y, Altlas L E ,Marks R J. The use of cone-shaped kernels for generalized time-frequency representations of nonstationary signals[J].IEEE Transactions on Acoustics, Speech, and Signal Processing,1990,38(7):1084-1091.

[10]Wu D, Morris J M.Time-frequency representations using a radial butterworth kernel[C]. IEEE-SP Int’l. Symp. on Time-Freq. and Time-Scale Anal, Philadelphia, PA. 1994: 60-63.

[11]王曉凱, 高靜懷, 何洋洋. 基于時頻自適應最優核的時頻分析方法[J]. 系統工程與電子技術, 2010, 32(1): 22-26.

WANG Xiao-kai, GAO Jing-huai, He Yang-yang, Time-frequency analysis based on time-frequency-adaptive optimal-kernel[J]. Systems Engineering and Electronics, 2010, 32(1): 22-26.

[12]Yan R, Gao R X. Base wavelet selection for bearing vibration signal analysis[J]. International Journal of Wavelets, Multiresolution and Information Processing, 2009, 7(4): 411-426.

[13]趙學智,陳統堅,葉邦彥,等. 基于參數方程的小波基自適應選擇[J]. 機械工程學報, 2005, 40(11): 123-128.

ZHAO Xue-zhi, CHENG Tong-jian ,YE Bang-yan,et al. Adaptive selection of wavelet based on parametr equation [J]. Chinese Journal of Mechanical Engineering, 2005, 40(11): 123-128.

[14]曾復. 裂紋轉子非線性振動機理及實驗研究[D]. 杭州:浙江大學, 2001.

[15]李志農. 時序模型盲辨識在旋轉機械故障診斷中的應用研究[D]. 杭州：浙江大學, 2002.