大跨度柱殼屋蓋基于半無矩理論簡化計算方法研究＊

白志強，劉 元

（1.濰坊學院，山東 濰坊 261061；2.中國建筑標準設計研究院有限公司，北京 100048）

柱殼由于其良好的受力性能，在船舶工業中應用較為廣泛，關于柱殼的受力分析，很多學者基于經典彈性力學理論，對柱殼的解析解法進行了積極的探索［1-2］。近幾十年來，殼體結構在建筑中的應用愈加廣泛，尤其是球面網殼、扁網殼等鋼網格結構在大跨建筑中應用日趨成熟。而對于混凝土柱殼結構的應用比較少，因此，積極探索混凝土柱殼結構的簡化分析方法對推動柱殼結構在工程實踐中的應用是非常必要的。

薄壁柱殼由于其在縱向曲率為零，在計算、設計、制造及施工過程中比雙曲扁殼結構要簡單方便的多，這也是環向開敞的柱殼可應用于各種工業與民用大跨度結構中的優勢之一。一般來講，頂蓋柱殼的計算是相當繁瑣的，但對于薄壁柱殼，面內次要方向的彎矩應力相對于其他應力分量很小，可以忽略，可考慮半無矩理論的簡化方法進行計算。單建［3］以結構力學桿系結構為例，分析了無矩解法的誤差問題。徐烈煊［4］采用半無矩理論簡化分析方法計算了直線邊帶有直梁的柱殼結構受力，并與Donnell彎曲理論和Schorer簡化理論所得結果進行了比較。本文基于弗拉索夫提出的半無矩理論，求解一對邊簡支的柱面薄殼屋蓋結構的內力和位移，并與有限元分析結果進行了比較。

如果圓柱殼的直線邊長度a與圓柱殼在水平面內的投影寬度b 之比大于1.5，縱向荷載q1=0，環向荷載q2及法向荷載q3都只沿環向變化，即可按半無矩理論簡化計算。半無矩理論是丹尼爾彎曲理論基本假設的進一步簡化：1）在垂直于母線方向橫截面上，彎矩和扭矩可以忽略（M1=M12=0）；2）不計中面的環向線應變和切應變，也就是取ε2=ε12=0，并且不計環向曲率的改變，即x2=0（于是α為常量的橫截面的中線不變形，而且保持垂直于縱線）；3）忽略泊松比的影響，即μ=0。

1 柱殼半無矩簡化分析方法的基本方程［5］

圓柱殼的尺寸如圖1所示：

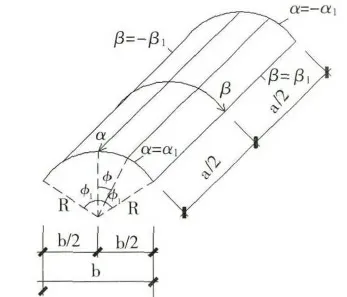
圖1 柱殼坐標及符號

引入無量綱坐標：

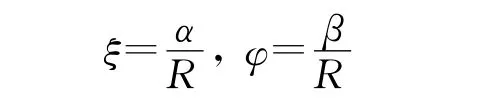
圓柱殼在q1q2q3作用下的平衡微分方程可以寫成：

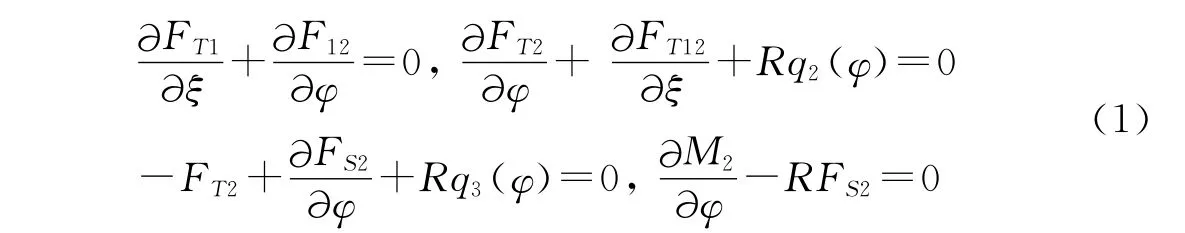
由物理方程及幾何方程得出方程如下：

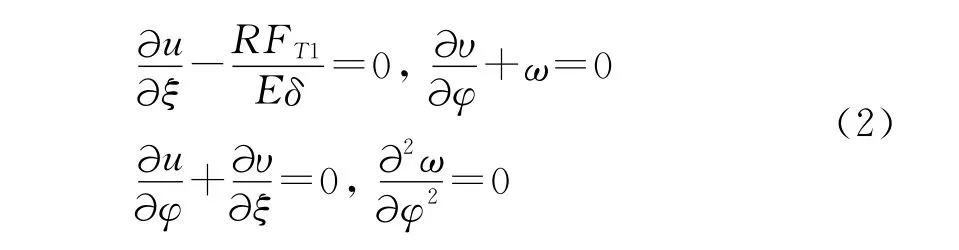
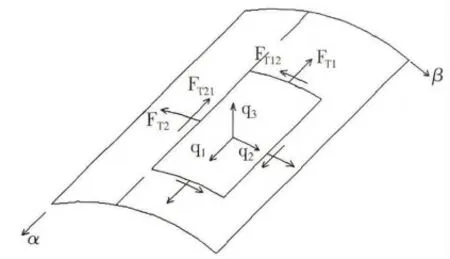
圖2 柱殼微分單元受力

而邊界條件可以表示為：

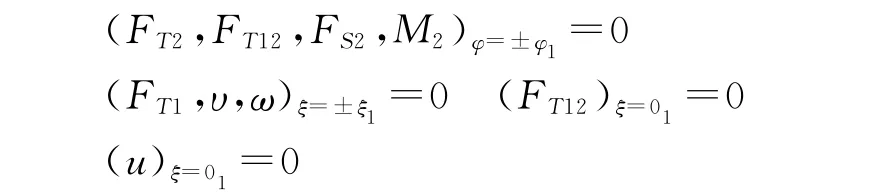
基于之前的假定，殼體橫截面上的正應力和直梁橫截面上的彎曲應力一樣，和截面的M 成正比。此柱殼橫截面彎矩圖沿縱向呈拋物線變化（見圖2），故M 正于與（α2-α12），也就正比于（ξ2-）。由于柱殼橫截面上的M1已經假定為零，可見上述的M 只與FT1即δσ1的合成，而

其中f（φ）=C1φ3+C2φ2+C3φ+C4。

將FT1表達式代入基本方程，結合邊界條件可得出：

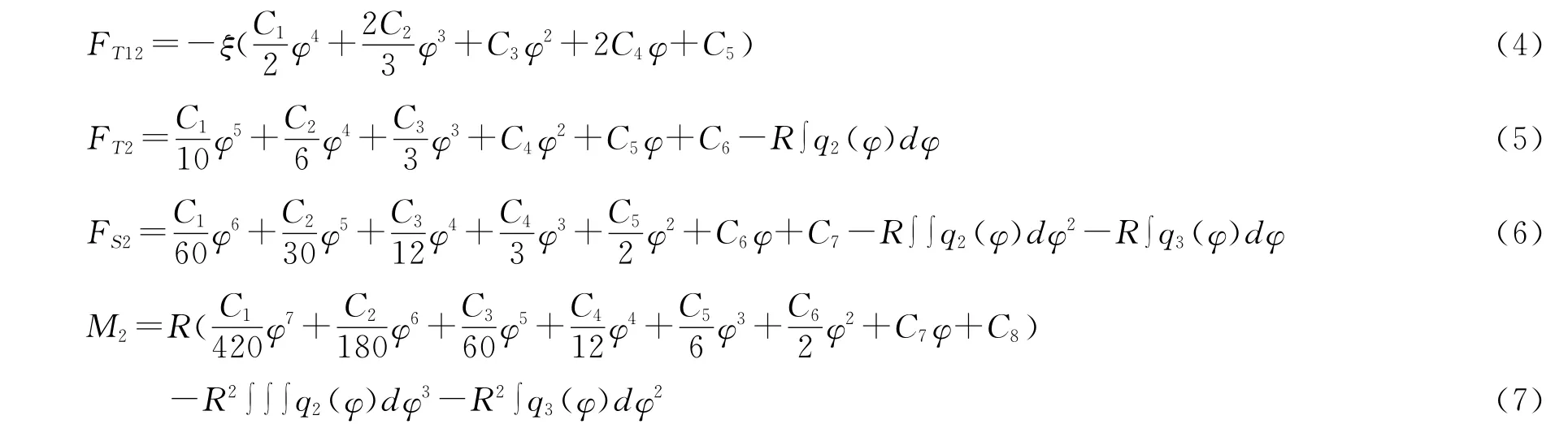
此處，由于C6C7C8為待定常數，已起到附加常數的作用，故積分式的附加常數可以取零。

柱殼中面位移的表達式為：

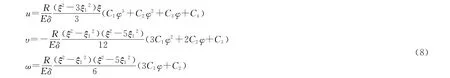
八個待定常數C1至C8可以由邊界條件完全確定。在對稱荷載作用下，q2（φ）是φ 的奇函數，q3（φ）是φ 的偶函數，因而u，ω，FT1，FT2，M2是φ 的偶函數，而υ，FT12，FS2是φ 的奇函數，這時有C1=C3=C5=C7=0，只需由四個方程求C2，C4，C6，C8。若在反對稱荷載作用下，同理可利用上述性質簡化計算相應四個待定常數C1，C3，C5，C7。對于一般荷載，可分解成對稱和反對稱荷載，疊加求之。

2 算例分析

圓柱殼屋面，厚度0.15m，拱的半徑為20.0m 的圓曲線，長度分別取為36m 和60m（對應的，半圓心角30°，側向長邊方向鉸支，曲邊自由，密度2500kg／m3，C30混凝土，材料彈性模量30GPa，試分析其在自重作用下的內力以及變形情況。

在屋蓋自重作用下，自重荷載為對稱荷載，滿足以上敘述的簡化求解條件。

按半無矩理論簡化方法求得跨中柱殼頂點處（α=β=0）的平行直線邊的內力FT1和徑向位移ω。

同時，采用ansys軟件建立有限元模型，兩簡支端曲梁采用beam4單元模擬，柱殼屋蓋采用shell181單元模擬，考慮泊松比為0.2，在cylindrical坐標系下，得到跨中柱殼頂點的平行直線邊的內力FT1和徑向位移ω。結果見表1。

表1 兩種計算方法所得FT1和ω

3 結果分析

通過以上的計算結果可以看出，對應沿母線方向的FT1值，半無矩理論算得的結果值比有限元算的的結果均偏大，跨度為36m 的結構運用半無矩理論的計算結果大了近60%，FT1大了跨度為60m 的柱殼結構結果偏大了一倍。主要原因在于采用半無矩理論簡化計算時，過多的近似 （不考慮泊松比，不考慮環向應變等）使得計算結果過于保守。

同時在進行徑向位移計算的過程中，由于半無矩理論運用的前提假定，使得中性面不發生變形，頂點處的最大位移為-0.0293m 和-0.2260，而ansys分析結果同位置處的位移為0.0182m 和0.01677m（沿徑向背向圓心）。但由于在有限元建模過程中，材料屬性采用各向同性材料模擬，在計算過程中考慮了環向切應變和環向線應變，考慮了環向曲率的改變，因此變形結果在柱殼頂點有沿徑向背向圓心方向的位移，在柱殼的直線邊界處，沿徑向的位移最大，分別達到-0.172m 和-0.282m （方向沿徑向指向圓心）。如圖3、圖4所示。

圖3 36m 跨柱殼處截面的變形

圖4 60m 跨柱殼處截面的變形

從結果比較來看，基于半無矩理論的簡化方法FT1計算結果較之數值計算結果明顯偏大；位移計算結果盡管在同一個數量級內，但由于簡化方法在計算過程中忽略了環向線應變和切應變，同時忽略環向曲率等過多的近似，使得計算的位移變形形態和有限元實體建模分析所得的變形結果又較大的差異，而有限元的變形趨勢基本符合實際的受力特點，有柱殼弧線被 “壓扁”的趨勢，如圖5和圖6。

圖5 36m 跨柱殼的變形云圖

圖6 60m 跨柱殼的變形云圖

4 結論

（1）通過比較兩種方法所得的結果，可得知基于半無矩理論的簡化計算所得跨中頂點處內力值FT1結果與數值分析方法結果保持在一個數量級之內，簡化方法所得結果偏保守。計算的徑向位移變形分布與數值分析結果有明顯差異。由于數值分析計算結果并沒有過多的近似假定，ansys建模過程中，選擇各構件模擬單元時，盡可能地反映各構件的實際受力特點，因此有限元分析結果能夠較精確地反映柱殼結構實際受力情況和變形情況。

（2）基于本文的分析可知，半無矩理論的分析結果與有限元分析結果存在明顯偏差，建議在概念設計階段可通過半無矩理論簡化方法近似估計FT1的受力及ω 的取值，在精細分析階段，應對誤差足夠重視；對于兩端簡支柱殼結構的精確計算，有限元分析方法應作為首選方法。

［1］王燕舞.對稱雙圓弧柱殼強度及穩定性解析計算方法研究［D］.哈爾濱工程大學，2004.

［2］姚文.圓柱殼結構在非均勻荷載作用下的強度分析［D］.哈爾濱工程大學，2007.

［3］單建，宋九祥.結構力學中擬無矩狀態的計算問題［J］.力學與實踐，2005，27（1）：70-71.

［4］徐烈煊.圓柱殼的半無矩理論分析［J］.武漢理工大學學報，2004，26（1）：72-75.

［5］徐芝綸.彈性力學（上冊）［M］.4版.北京：高等教育出版社，2006：301-330.