反應流體的移動網格動理學格式

甄亞欣, 倪國喜（.北京應用物理與計算數學研究所,計算物理實驗室,北京 00088；2.華北電力大學,數理系,北京 02206）

反應流體的移動網格動理學格式

甄亞欣1,2, 倪國喜1
（1.北京應用物理與計算數學研究所,計算物理實驗室,北京 100088；2.華北電力大學,數理系,北京 102206）

在移動網格上構造一種反應流的動理學格式.首先利用BGK模型推導含化學反應的流體力學方程組,并利用其積分形式構造移動網格上離散格式,再利用自適應移動網格方法得到網格速度,最后利用時間精確的動理學數值方法構造數值通量,得到移動網格單元上新的物理量.一維與二維的數值實驗表明這種格式同時具有高精度、高分辨率的特點.

反應流體力學方程；動理學格式；自適應移動網格方法

0 引言

含化學反應的流體動力學研究是爆轟流體力學的最重要部分,爆轟流體力學是伴隨化學反應的強沖擊波的傳播過程,人們對其理論研究與相關的數值模擬的研究有較長的歷史[1].早在1899年,Chapman及Jouguet等對爆轟現象作了簡單的一維理論描述,形成所謂C-J理論[2－3],該理論是借助氣體動力學原理而闡釋的.之后,Zel'dovich、Neumann與D?ring各自獨立對C-J理論的假設和論證作了改進,提出所謂的ZND理論[4－6],它比C-J理論更接近實際情況,上述兩種理論被稱為爆轟波的經典理論,它們都是一維理論.二十世紀50年代,通過實驗的詳細觀察,發現爆轟波波陣面包含復雜的三維結構,這種結構被解釋為入射波,反射波和馬赫波構成的三波結構.到二十世紀50－60年代,人們進行了大量的試驗研究,實驗結果顯示：反應區末端狀態參數落在弱解附近,而不是C-J參數,說明實際爆轟比C-J理論和ZND模型更為復雜.之后,Kirwood和Wood[7]推廣了一維定常反應理論,指出定常爆轟具有弱解的可能性將隨著流體的復雜性增加而增加.弱解模型為實驗數據與一維理論的偏離作出了一種理論解釋.從二十世紀60年代開始, Erpenbeck[8]提出了爆轟的線性穩定性理論,對一維爆轟定常解的穩定性進行了分析.后來又有人提出“方波”穩定性理論.由于實驗測量技術和數值模擬工具的限制,以及固有的復雜性,研究工作有一些進展,但還存在許多困難和問題.

隨著計算方法與計算技術的發展,爆轟流體力學數值模擬方法取得了很大的進步[9],目前最常用的有歐拉方法與拉氏方法.歐拉方法對應流體力學方程的Euler形式,網格固定不動,除了考慮由源項引起的變化,還必須考慮通過網格的物理量輸運.然而歐拉方法在模擬多介質流動時會遇到許多問題,多介質流動問題模擬的關鍵之一是要確定物質界面和自由面,對于多介質界面追蹤已經發展了一些有效的方法,如Hirt和Nichols[10]提出的體積份額法,Glimm[11]等提出的波陣面追蹤法.這些方法在保持守恒性與克服震蕩等方面還存在一些問題.拉氏方法對應流體力學方程的拉格朗日形式,由于不含輸運項,拉氏方法計算公式簡單,網格隨流體運動,數值耗散小,界面清晰.拉氏方法可以分為兩種形式,一種是交錯網格型,另一種是以Godunov方法為基礎的單元中心型.與交錯網格方法不同,單元中心型的所有物理量定義在網格中心,它的優點是可以給出較為精確的壓力與邊界條件,可以保持能量守恒,該方法的不足之處是網格節點的拉氏速度由某種插值或者優化的形式獲得,從而導致該方法的非物理變形.為抑制網格的扭曲變形,可以在拉氏計算中加入網格重分以提高算法的抗變形能力,Hirt和Nichols[12]所開創的ALE方法就是基于這一思想發展起來的,利用ALE方法模擬多介質流動日益受到重視,但守恒性、相容性等問題還沒能很好的解決.

移動網格方法是與ALE方法比較接近的一種數值方法,Azarenok和Tang[13]發展了基于守恒插值的移動網格方法,它部分克服了ALE方法所遇到的困難,另一種移動網格方法由Harten等[14]開創,它在時空多面體上運用有限體積方法,避免了顯式的重映,后被發展到高維空間,并用于化學反應流的數值模擬,但離散格式復雜,在高維時很難把握數值精度.結合動理學方法,Ni等[15]進一步發展了移動網格方法.動理學數值方法是目前流體力學數值模擬中的一種重要的方法,它從微觀層次獲取宏觀的數值通量,與通常的數值方法相比較,有更多的物理內涵,因而可以提供更多的信息,其時間積分是精確的.動理學數值方法的基本思想是利用流體的微觀描述與宏觀描述的等價性,宏觀Euler方程與Navier-Stokes方程可以利用Boltzmann方程得到[16].利用其簡化模型,Deshpande和Mandal等[17－18]發展了一種動理學數值方法,他們將Courant-Isaacson-Reeves迎風算法用于無碰撞的Boltzmann方程,得到動力學通量向量分裂法（即KFVS方法）.之后基于Bhatnagar-Gross-Krook（BGK）模型的動理學數值方法也迅速發展起來[19－21].Xu和Lian在這一方面發展了一套比較系統的方法,并用于多介質與稀薄流等問題的數值模擬[22－24].基于動理學移動網格方法是一種無重映移動網格方法,它避開了傳統的移動網格方法中物理量重映帶來的誤差.

本文從動理學BGK模型出發,利用經典的Chapman-Enskog展開,導出含化學反應的流體力學方程,在動理學數值方法的基礎上,結合移動網格技術構造了含化學反應的流體力學動理學格式.

1 移動網格反應流體力學的動理學數值方法

本節從修正的BGK模型出發,利用Chapman-Enskog展開,推導反應流體力學方程組,利用其積分形式,給出在運動標架下的離散形式,再結合移動網格方法,確定網格移動速度,實現物理量的更新.

1.1 反應流體力學方程組的BGK模型

以修正的二維的BGK模型為例,推導反應流體力學方程組,二維BGK方程為

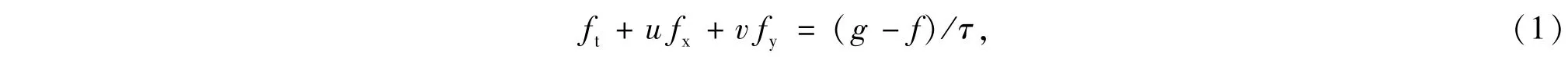
其中f是微觀粒子的分布函數,g是逼近f的平衡態分布函數,（u,v）是微觀粒子的運動速度,在包含多組分時,f與g可表示為

其中z為組分參量,在描述單介質的流體時,f與g一般表示為

它們與z無關,這里增加一個自由度后,就可以從BGK模型方程得到擴展的含化學反應的流體力學方程.相應地,多組分的平衡態分布有

這里λ＝m/（2kT）,m是微觀粒子的質量,k是Boltzamn常數,T是宏觀溫度,自由度K＝（5－3γ）/（γ－1）＋1,ξ2＝

宏觀物理量與微觀的分布函數的關系為

其中dΞ ＝d u d v d z dξ,dξ＝dξ1dξ2…dξK,Ψ ＝（ψ1,ψ2,ψ3,ψ4,ψ5）＝（1,u,v,z,（u2＋v2＋ξ2）/2）.

由流體質量、動量、能量的守恒性,得到守恒約束條件

從BGK模型方程得到反應流體力學方程,同樣可以利用Chapman-Enskog展開,零階的Chapman-Enskog展開式f＝g,代入方程（1）,作矩得

其中Ψ ＝[1,u,v,z,（u2＋v2＋ξ2）/2],寫成分量形式可得多組分的流體的Euler方程

其中總能量E＝ρ[U2＋V2＋（K＋2）/（2λ）]/2,壓力P＝ρ/（2λ）.

若考慮化學反應,這時p＝p（ρ,e,z）,其中的z為組分變量,參數z由化學反應率方程確定

不同的化學反應類型有不同類型的表式,對理想流體的化學反應,一般取指數形式的Arrhenius反應率

對于給定化學反應率的流體,與方程（2）對應的包含化學反應的流體力學方程為

其中Q為化學反應的熱能.

1.2 移動網格上的離散格式

對于含化學反應的無粘的可壓縮的流體力學方程,為構造移動網格上的動理學數值方法,考慮運動控制體Ω（t）,設其邊界速度為Ug,則在Ω（t）上與方程組（3）對應的的積分形式可表示為

其中S（t）是控制體Ω（t）的邊界,n是邊界單位外法向,ρ,p,E和U＝（U,V）分別為流體的密度,壓強,比總能和速度.記e＝E－U2/2為比內能.當Ug＝0,方程組（4）是歐拉坐標的積分形式.當Ug＝U時,則為拉氏坐標的積分形式.

其中（·）Ω為Ω上的均值,

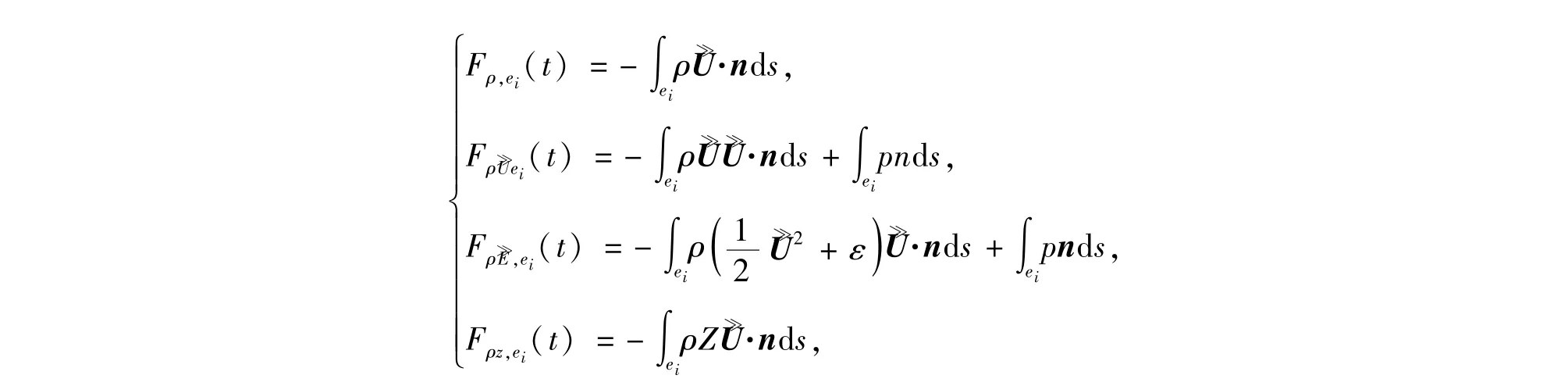
這里Fρ,ei,,Fρz,ei分別為通過邊界ei的質量通量、動量通量和能量通量.

為得到分量形式的離散方程,將邊界速度分解為法向與切向速度分量,記邊界ei法向方向為n＝（cosα, sinα）,速度為U＝（U,V）,則法向速度′和切向速度分量為

則可將離散方程組（5）寫為

其中

方程組（6）是移動網格下有限體積半離散格式.定義不同時刻的控制體Ω′＝Ω（tn＋1）和Ω＝Ω（tn）,控制體上質量、動量和能量的質量平均值定義為

對半離散形式（6）,由于動理學通量是時間的顯函數,從時間步tn到tn＋1積分,得到方程組（6）的全離散格式,時間離散是精確的.

1.3 動理學數值通量

在這一節,將利用方程（1）解的表達式構造數值通量,對于方向分裂格式,數值通量歸結為一維的情形,與方程（1）對應的一維的BGK方程的解可表示為

其中x′＝x－u（t－t′）.有了邊界的分布函數,就能得到邊界的數值通量,這樣只需在邊界點構造非平衡的初始分布f0與平衡分布函數g.

對非平衡的初始分布f0,不失一般性可設邊界點xj＋1/2＝0,令

這里al,r,Al,r進一步可展開為

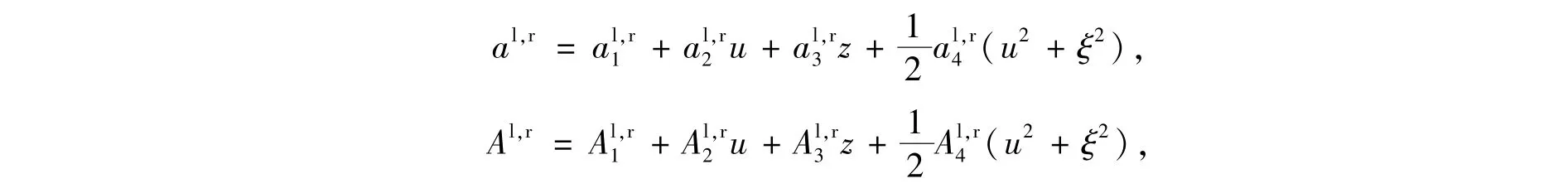
對于平衡態g,不妨設它為（x＝0,t＝0）附近的平衡態,可構造為

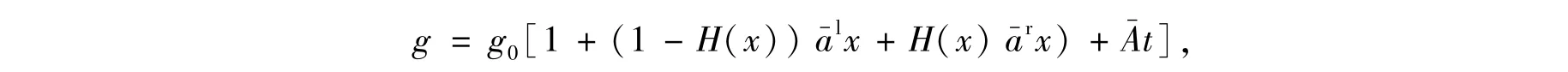
同樣,

利用文獻[19]中類似方法可計算出所有的系數.

將上述得到的非平衡的初始分布f0與平衡態分布g代入解的表達式（7）,進行簡單的積分運算可得

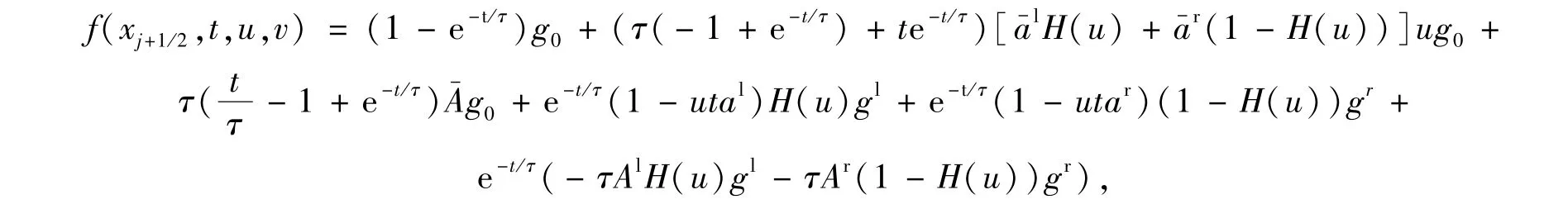
這樣可以積分得到邊界通量,

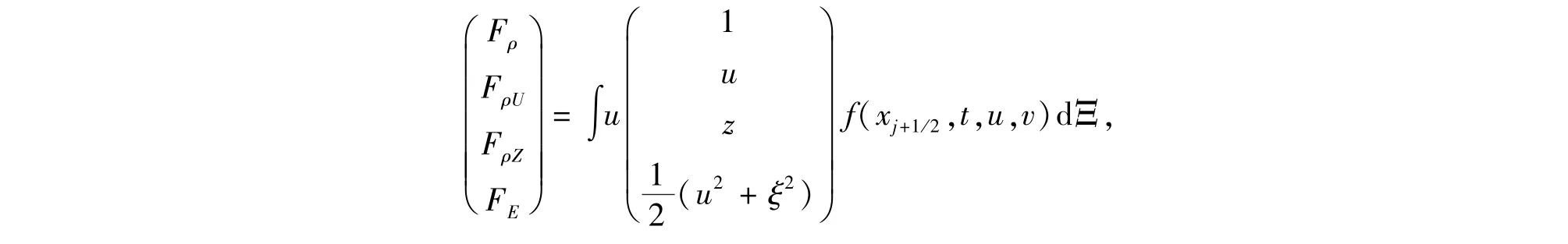
按邊界法向與切向方向投影,再代入式（6）就可更新單元上的物理量.

1.4 網格移動速度

得到邊界通量后,剩下就是要確定網格速度,為得到網格移動速度,只需要得到網格節點的新時刻的位置,利用

就可得到節點速度,其中Xn＋1和Xn分別為新舊網格節點坐標,Δt是時間步長,利用線性關系就得到邊界上各點的速度分布.

新時刻網格節點位置利用變分原理得到,假設x＝x（ξ）是計算域到物理域的坐標映射,ξ＝ξ（x）是逆映射.定義計算區域網格能量泛函為

其中d是空間維數,Gk是給定的對稱正定矩陣,為簡單起見,這里取為Gk＝w I,其中I是單位矩陣,w是非負加權函數.能量泛函（8）對應的歐拉－拉格朗日方程為

利用有限體積方法可得到網格移動方程的離散格式,參見文獻[22],對二維的網格方程,權函數w取值為

其中熵s＝p/ργ,uξ為相應單元的物理量,α1和α2是可調非負參數.

2 數值實驗

含化學反應的流體動力學行為比較復雜,實驗結果很少,這里利用上節構造的數值方法給出幾個典型算例的數值模擬結果.

一維反應流體數值實驗

這是一個穩態的含化學反應的流體力學問題,激波前的狀態為

反應率中的參數分別為：Ea＝14.0,Q＝14.0,γ＝1.4.波后狀態利用下列公式計算[1],

圖1 密度的數值模擬結果與精確解Fig.1 Density comparison between exact solution （bold line）and numerical solution（circle）

圖2 壓力的數值模擬結果與精確解Fig.2 Pressure comparison between exact solution and numerical solution

圖3 質量分數的數值結果（未反應區的值為1.0,反應完成區為0.0.）Fig.3 Mass fraction distribution between 1.0 and 0.0

其中v＝1/ρ,可得C-J狀態的值

Von Newmann狀態的值由公式

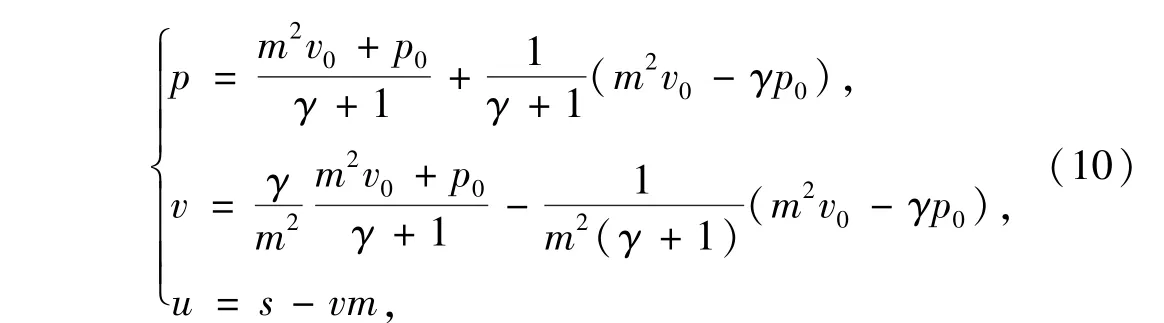
得到ρvn＝4.852 1,pvn＝24.512.其中

計算區域為[0,4],網格數為800,圖1－2分別給出了密度與壓力的數值結果與解析值的比較.圖3為同一時刻的質量分數的數值結果,它表明這種數值格式有很高的分辨率.

二維反應流體的數值實驗

這是非穩態的數值算例,計算區域為[0,4.0]×[0,1.0],網格數為480×120,沖擊波由左至右傳播,波前狀態為ρ＝1.0.p＝1.0,u＝0.0.沖擊波波速為s＝5.441 9,波后狀態可以利用式（9）與（10）得到, y方向按正弦曲線作擾動,如圖4為初始分布,圖5為密度等值線圖,圖6則是相應時刻的局部網格分布.

圖4 二維初始分布（左右兩側均為分片常數,y方向為兩周期的正弦擾動.）Fig.4 Initial distribution with piecewise constants

圖5 密度等值線分布Fig.5 Distribution of density contours

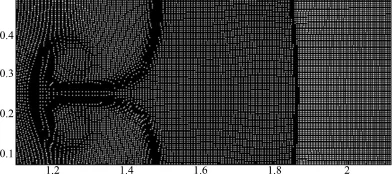
圖6 局部網格分布（顯示的網格數為實際數量的1/10.）Fig.6 Localmesh distributions（1/10 meshes are shown.）

3 結論

利用BGK模型推導了含化學反應的流體力學方程組,構造了移動網格上離散格式,利用自適應移動網格方法得到網格速度,由動理學數值方法構造數值通量,這樣得到了移動網格單元上新的物理量.一維與二維的數值實驗表明這種格式同時具有高精度、高分辨率的特點.這種方法可以推廣到一般狀態方程的反應流體力學方程組.

[1] FickettW,DavisW C.Detonation[M].Berkeley：University of California Press,1979.

[2] Chapman D L.VI.On the rate of explosion in gases[J].Philosophical Magazine Series 5,1899,47（284）：90－104.

[3] Jouguet JC E.On the propagation of chemical reactions in gases[J].Journal des Mathématiques Pures et Appliquées,Series 6,1905,1：347－425.

[4] Zel′dovich Y B.On the theory of the propagation of detonation in gaseous systems[J].Journal of Experimental and Theoretical Physics,1940,10：542－568.

[5] Neumann JV.Theory of detonation waves[R].Office of Scientific Research and Development,Report No.549,Ballistic Research Laboratory File No.X－122.Aberdeen Proving Ground,Maryland,1942.

[6] D?ring W.On the detonation process in gases[J].Annals of Physics,1953,43：421－436.

[7] Kirwood JG,Wood W W.Structure of a steady state plane detonation wave with finite reaction rate[J].The Journal ofChemical Physics,1954,22：1915－1919.

[8] Erpenbeck JJ.Stability of idealized one reaction detonation[J].Physical Fluids,1964,7：684－696.

[9] 孫錦山,朱建士.理論爆轟物理[M].北京：國防工業出版社,1995.

[10] Hirt CW,Nichols B D.Volume of fluid（VOF）method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39（1）：201－225.

[11] Glimm J,Grove JW,Li X,Zhao N.Simple front tracking[J].Contemporary Mathematics,1999,238：133－149.

[12] Hirt CW,Nichols B D.An arbitrary Lagrangian Eulerian computingmethod for all flow speed[J].Journal of Computational Physics,1997,135：203－216.

[13] Azarenok B N,Tang T.Second-order Godunov-type scheme for reactive flow calculations on movingmeshes[J].Journal of Computational Physics,2005,206：48－80.

[14] Harten A,Hyman J M.Self adjusting grid methods for one-dimensional hyperbolic conservation law[J],Journal of Computational Physics,1983,50：235－269.

[15] Ni G X,Jiang S,Xu K.Remapping-free ALE-type kinetic method for flow computations[J].Journal of Computational Physics,2009,228：3154－3171.

[16] Chapman S,Cowling TG.Themathematical theory of non-uniform gases[M].Cambridge University Press,1990.

[17] Mandal JC,Deshpande M.Kinetic flux vector splitting for Euler equations[J].Computers Fluids,1994,23（2）：447－478.

[18] Chu C K.Kinetic-theoretic description of the formation of a shock wave[J].Physical Fluids,1965,8：12－22.

[19] Lei G,LiW,Ren Y.A high-order unstructured-gird WENO FVM for compressible flow computation[J].Chinese Journal of Computational Physics,2011,28（5）：633－640.

[20] Xu X,Ni G.A high-ordermovingmesh kinetic scheme based on WENO reconstruction for compressible flows[J].Chinese Journal of Computational Physics,2013,30（4）：509－514.

[21] Li Z,Yu X,Zhao G,Feng T.A RKDG finite elementmethod for Lagrangian Euler equation in one dimension[J].Chinese Journal of Computational Physics,2014,31（1）：1－10.

[22] Xu K.A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J].Journal of Computational Physics,2001,171：289－335.

[23] Lian Y S,Xu K.Gas-kinetic scheme for multimaterial flows and its application in chemical reactions[J].Journal of Computational Physics,2000,163：349－375.

[24] Lian Y S,Xu K.Gas-kinetic scheme for reactive flows[J].Computers＆fluids,2000,29：725－736.

[25] Tang H Z,Tang T.Adaptivemeshmethods for one-and two-dimensional hyperbolic conservation laws[J].SIAM Journal on Numerical Analysis,2003,41：487－515.

Adaptive M oving M esh K inetic Scheme for Reactive Fluids

ZHEN Yaxin1,2, NIGuoxi1
（1.LCP,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China；
2.School ofMathematics and Physics,North China Electric Power University,Beijing 102206,China）

We concern extension of gas-kinetic scheme of BGK type to reactive fluids,and develop an adaptivemovingmeshes BGK scheme（AMMBGK）.We derive systems from amass fraction BGK model for detonation fluids,including both inviscid and viscous reactive flow systems.Then,based on a BGK type scheme and splitting method that splits system into fluid part and part of energy released from reaction process,we presentamass fraction BGK scheme onmovingmeshes for reactive flows.Numerical results validate availability of the gas-kinetic scheme in simulation of reactive fluids.

reactive fluids；mass fraction BGK model；gas kinetic scheme；adaptivemovingmeshes

1001-246X（2015）06-0677-08

O351

A

2014－11－04；

2015－02－02

國家自然科學基金（91130020,11402087）,國防基礎科研計劃（B1520133015）及計算物理實驗室基金資助項目

甄亞欣（1983－）,女,博士,講師,從事計算流體力學方法研究,E-mail：yasine_zhen＠163.com