同步坐標下無刷雙饋電機無源性控制

同步坐標下無刷雙饋電機無源性控制*

陳集思1，楊俊華1，黃健健2，吳捷3

(1. 廣東工業大學 自動化學院,廣東 廣州510006;

2. 機械工業部深圳設計研究院有限公司,廣東 深圳518000;

3. 華南理工大學 電力學院,廣東 廣州510641)

摘要：針對無刷雙饋電機非線性PID控制方案中轉速和負載轉矩動態響應性能差，負載突變時易引起振蕩等問題，提出無源性控制策略。根據無刷雙饋電機同步速旋轉坐標系下的電壓、磁鏈和轉矩方程，建立電機的歐拉-拉格朗日模型；從能量角度分析電機電氣子系統與機械子系統的無源性，設計電機的轉矩控制器和轉速控制器。為改善系統動態響應，降低其對參數變化的靈敏度，通過在控制器中加入非線性阻尼，實現系統的快速收斂。基于MATLAB/Simulink環境搭建了無刷雙饋電機無源性控制的仿真模型，仿真結果表明，無源性控制策略可快速跟蹤給定轉速，動態響應性能好，全局穩定、魯棒性好。

關鍵詞：無刷雙饋電機； 無源性控制； 非線性阻尼； 動態響應； 魯棒性

基金項目：* 國家自然科學基金資助項目(51307025,5177050,51407035);廣東省高等學校科技創新項目(2013KJCX0059);廣東高校優秀青年創新人才培養計劃項目資助(2012LYM_0052;2013LYM_0019)

通訊作者：陳集思

中圖分類號：TM 301.2;TP 273文獻標志碼： A

收稿日期：2015-03-26

Passivity-Based Control Strategies of Brushless Doubly-Fed Machine

CHENJisi1,YANGJunhua1,HUANGJianjian2,WUJie3

(1. School of Automation, GuangdongUniversity of Technology, Guangzhou 510006, China;

2. Shenzhen Machinery Institure Architectural Design, Co.， Ltd.， Shenzhen 518000, China;

3. School of Electric Power, South China University of Technology, Guangzhou 510641, China )

Abstract：A novel passive control strategy was proposed to improve the dynamic response performance of the speed and load torque of the brushless doubly-fed machine(BDFM) with the nonlinear PID control scheme,and the oscillation as the load changes suddenly. The Euler-Lagrangian model of BDFM was established based on the equations of the voltage,flux and torque of BDFM in synchronous speed rotary coordinate system. The passivity of the electrical subsystems and mechanical subsystems of the machine were analysized by the view of energy, and the controllers of the torque and speed were designed.In order to improve the system dynamic response and reduce its sensitivity to parameter variations, the nonlinear damping was added into the controller to make the system achieve fast convergence.A novel simulation model of BDFM with passivity control strategy was built in MATLAB/Simulink environment.The simulation results showed that a given speed of BDFM could be fastly tracked, BDFM had good dynamic performance,global stability and good robustness with the passive control strategy.

Key words： brushless doubly-fed machine; passivity based control; nonlinear damping; dynamic response; robustness

0引言

無刷雙饋電機(Brushless Doubly-Fed Machi-nes, BDFM)是一種新型交流調速電機。BDFM結構簡單穩固、功率因數可調、調速控制裝置容量小、運行模式靈活，在可調速驅動系統和變速恒頻發電領域應用前景廣泛。近年來，國內外學者對BDFM進行了較多研究，建立了較為準確實用的數學模型[1]，提出標量控制[2]、矢量控制[3]、轉子磁場定向控制[4]、直接轉矩控制[5-9]、智能控制[10-12]、自適應控制[13-15]等多種控制策略。文獻[4]分別將BDFM的功率繞組和控制繞組在各自的同步坐標系下進行磁場定向，數學模型和轉子磁場定向控制策略得以簡化，控制性能良好。文獻[5]研究了一類無刷雙饋電機直接轉矩控制系統，結構簡單、計算量小，但磁鏈和轉矩脈動較大。為此，文獻[7]提出采用轉矩預測法，有效減小了轉矩脈動并改善了定子電流波形。文獻[10]通過引入轉矩預測控制策略，獲得了良好的動態性能。采用磁場定向矢量控制方案的BDFM調速系統，存在超調及動態穩定遲滯等問題，文獻[11]結合模糊控制和PI控制，控制效果明顯好于單獨的PI控制。文獻[12]設計了BDFM的PID神經網絡控制器，轉速跟蹤準確，但過分依賴于系統模型，對系統未建模動態和未知擾動亦未作出較好的估計和補償。基于波波夫超穩定性理論的模型參考自適應算法，文獻[13]提出了一種轉矩和磁鏈計算的新方法，改進了BDFM直接轉矩控制策略。BDFM是一個高階、多變量、非線性及強耦合系統，各類控制策略都存在局限性[16]。

無源性控制策略(Passivity Based Control， PBC)最早應用于機器人控制，由Omega等人將PBC的概念引入到電機控制中。各類電機，無非都是基于法拉第電磁感應定律進行機電能量變換，PBC強調從能量的觀點，考慮將電機處理成非線性控制對象，通過配置系統能量耗散特性方程中的無功分量，迫使系統總能量跟蹤期望的能量函數，并使系統的狀態變量漸近收斂至設定值。電機動態方程中的無功分量則不必抵消，其對系統能量平衡及穩定性無影響，控制器簡單、魯棒性好。文獻[17]研究了雙饋電機PBC的設計步驟，轉速外環與電流內環相互協調，保證了定轉子電流及轉速的漸近跟蹤。針對變速恒頻雙饋異步風力發電系統，文獻[18]提出了一種既能漸近跟蹤期望的定轉子電流和轉速，又可保持定子側單位功率因數運行的無源控制器，實現了風電系統的最大風能捕獲。文獻[19]設計了本質上是非線性反饋的PBC，實現了雙饋風力發電系統在負載轉矩時變未知情形下磁鏈、轉速的漸近跟蹤控制。文獻[20]論證了BDFM的無源性，給出了d-q軸旋轉坐標下的轉速控制器。

根據無源性控制理論，本文將BDFM的轉子磁鏈參考值作為轉矩控制器的輸入，并在轉矩控制器前加上線性調節器，通過漸近跟蹤磁鏈設定值，調節BDFM的轉速和轉矩。控制器中加入了非線性阻尼，系統收斂快速。

1BDFM的無源性分析

1.1BDFM的數學模型

BDFM定子的功率繞組直接接工頻電源，控制繞組通過變頻器與工頻電源連接。

功率繞組子系統在其同步旋轉坐標系下的d-q軸電壓和磁鏈方程為[21]

(1)

(2)

控制繞組子系統在其同步旋轉坐標系下的d-q軸電壓和磁鏈方程為

(3)

(4)

式中：uqp、udp、iqp、idp、ψqp、ψdp、rp、Lp、Lmpr、ψqrp、ψdrp——功率繞組的電壓、電流、磁鏈、電阻、自感、功率繞組與轉子之間的互感和功率繞組轉子磁鏈的q軸和d軸分量；

uqc、udc、iqc、idc、ψqc、ψdc、rc、Lc、Lmcr、ψqrc、ψdrc——控制繞組的電壓、電流、磁鏈、電阻、自感、控制繞組與轉子之間的互感和控制繞組中轉子磁鏈的q軸和d軸分量；

ωr、ωp、ωc、ωsp、ωsc——機械角速度、功率繞組和控制繞組的角頻率和轉差角速度；

D——微分算子；

上標p、c——功率繞組同步速坐標系、控制繞組同步速坐標系；

下標p、c、s、r——功率繞組、控制繞組、定子側、轉子側的物理量；

下標d、q——d-q坐標系下q、d軸分量。

BDFM的電磁轉矩方程為

Te=Tep+Tec

(5)

其中：

(6)

式中：Tep、Tec——功率繞組子系統和控制繞組子系統產生的電磁轉矩。

運動方程為

(7)

式中：J、Kd、Tl——轉子的轉動慣量、阻尼系數和負載轉矩。

1.2BDFM控制繞組的Euler-Lagrange系統

BDFM功率繞組與電網直接相連接，其電壓的大小和頻率由電網決定，通過調節BDFM控制繞組的電壓和頻率，就可以控制電機的運行模式。為分析BDFM的無源性，現將式(3)轉化為EL方程的形式，電流的狀態方程為

(8)

其中：

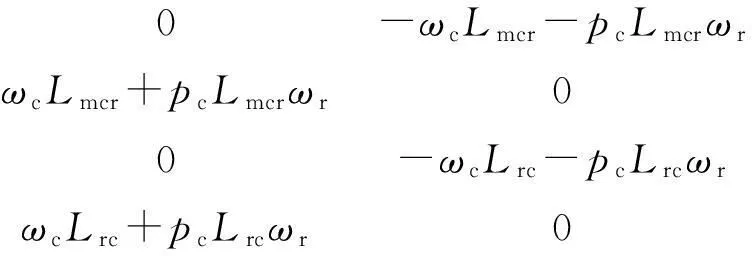
式中：u和i——控制繞組子系統的輸入電壓矢量和輸出電流矢量；

M和R——分別為控制繞組子系統的電感矩陣和電阻矩陣；

W——與控制繞組子系統有關的項；

C和CT——反對稱矩陣。

1.3BDFM控制繞組無源性分析

分別對BDFM控制繞組的電氣子系統和機械子系統進行無源性分析。

忽略繞組的電容效應，定義BDFM控制繞組中電氣部分的能量函數為

(9)

對時間求導：

(10)

將式(8)代入式(10)：

(11)

因C具有反對稱性，即iTCi=0，所以Ci項不會影響系統的能量變化，也就不會影響系統的穩定性。因此，在設計BDFM控制策略時，可忽略該部分的非線性因素，可以認為是一個配置系統無功分量的過程。

將式(11)兩邊進行積分可得

He(t)-He(0)=∫0tiTudτ-∫0tiTRidτ-

∫0tiTWddτ<∫0tiTudτ

(12)

式(12)左邊是控制繞組電氣子系統能量的增量，右邊為電機從電源獲取的能量。現將u視為電氣子系統輸入，則iT為子系統輸出。右邊第二項實際就是電氣子系統內部的電阻消耗、第三項則為電氣子系統中轉化為機械能部分的能量。式(12)表明，控制繞組電氣子系統磁場儲存能量的增加量，總是小于控制繞組從電源獲得的能量，所以電氣子系統是嚴格無源的。

假設BDFM轉軸為剛性，即BDFM機械部分存儲的能量全部為動能，則其能量函數可定義為

(13)

對式(13)進行時間求導后代入式(7)，積分后可得

(14)

式(14)左邊為機械子系統所增加的能量，右邊為機械子系統輸入的能量。若將Te-TL視為機械子系統輸入，ωm視為機械子系統輸出，則BDFM的機械子系統嚴格無源。

由并聯系統的無源性原理可知，因為電氣子系統和機械子系統均為嚴格無源的，故其并聯形成的整個BDFM系統也是嚴格無源的。功率繞組、控制繞組和機械三部分子系統的相互連接關系如圖1所示。

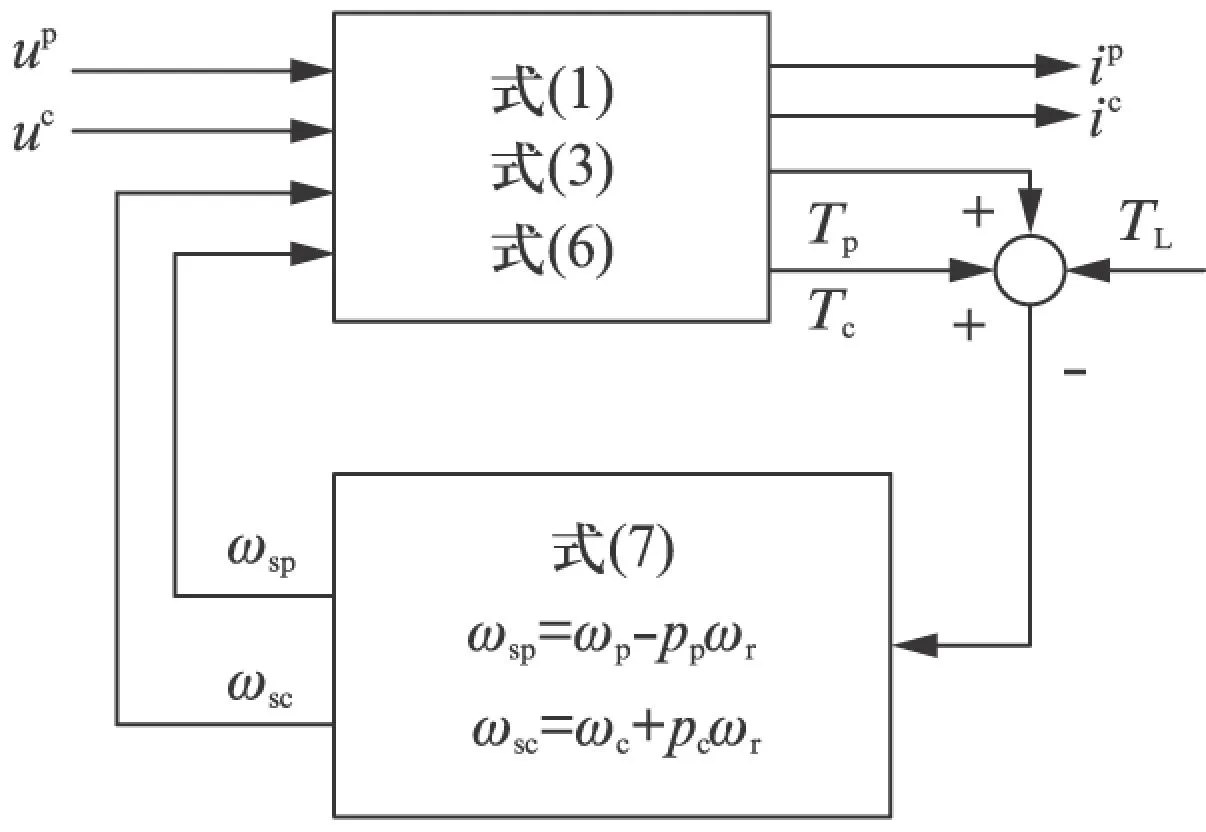
圖1　BDFM的反饋互聯結構

設計PBC方案時，可將控制繞組電氣子系統的能量存儲函數作為總的能量函數，機械子系統則可看作是電氣子系統的無源干擾。

2基于無源性的控制器設計

2.1轉矩控制器設計

為實現轉子磁場漸近矢量控制和電磁轉矩漸近跟蹤，制定如下控制目標：

(1) 電磁轉矩漸近跟蹤，即

(15)

(2) 控制繞組子系統轉子磁鏈q軸分量漸近定向，即

(16)

(3) 控制繞組子系統轉子磁鏈d軸分量漸近跟蹤，即

(17)

為此，定義實際狀態與狀態期望值之間的跟蹤誤差為

(18)

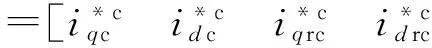
由方程(8)，可得到系統的誤差方程：

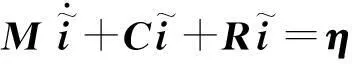
(19)

式中：η——作用于系統的擾動。

(20)

定義誤差方程的能量存儲函數為

(21)

求式(21)對時間的導數，有：

(22)

由于C為反對稱矩陣，所以式(22)右邊第一項為零，整理上式，可得

(23)

功率繞組與電網直接連接，計算功率繞組磁鏈時，可忽略其電阻壓降。即功率繞組磁鏈為

(24)

將功率繞組子系統的磁鏈與其對應的同步速旋轉坐標系的d軸重合，得到以下關系，即：

(25)

整理可得

(26)

在確定轉速下，功率繞組同步速坐標系中轉子電流分量將為恒定值。

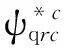
(27)

由式(3)的第3行可得到控制繞組的轉差角速度為

(28)

令η=0，由式(3)的1、2行可得PBC系統的控制律為

(29)

將式(27)、式(28)代入式(29)，化簡可得

(30)

為保證整個控制系統嚴格無源，改善系統動態響應并降低控制系統對參數變化的靈敏度，對控制量式(30)注入阻尼項，可得

(31)

式中：k——阻尼系數。

恒定阻尼注入，雖可改善系統動態響應，但會影響系統穩態性能，因此提出變阻尼控制策略。變阻尼通過跟蹤微分器實現，在電機起動或動態過程開始時采用大阻尼，隨后實行自動調節，從而改善動態響應。

針對BDFM的控制系統，所采用二階微分跟蹤器實現變阻尼的注入。若二階跟蹤微分器輸入一個信號v(t)，它將輸出兩個信號x1和x2，其中x1跟蹤輸入信號v(t)，x2作為v(t)的“近似微分”。其形式為

(33)

其中：

(34)

同理，在BDFM控制系統中注入變阻尼時，可在電機起動時注入較大阻尼，接近穩態時切換至較小阻尼。因此，將跟蹤微分器的輸出倒用，獲得變阻尼注入的形式為

(35)

其中：

(36)

式中：k1——起動時希望注入的阻尼值；

k2——接近穩態時希望注入的較小阻尼值；

k——阻尼輸出值。

2.2轉速控制器設計

基于無源性的BDFM轉矩控制系統，能夠漸近跟蹤時變的轉矩，只要建立轉速誤差反饋，采用比例積分調節器，就能夠得到下述參考轉矩方程：

(37)

式中：kp、ki——比例、積分增益。

可構建BDFM無源控制系統，如圖2所示。

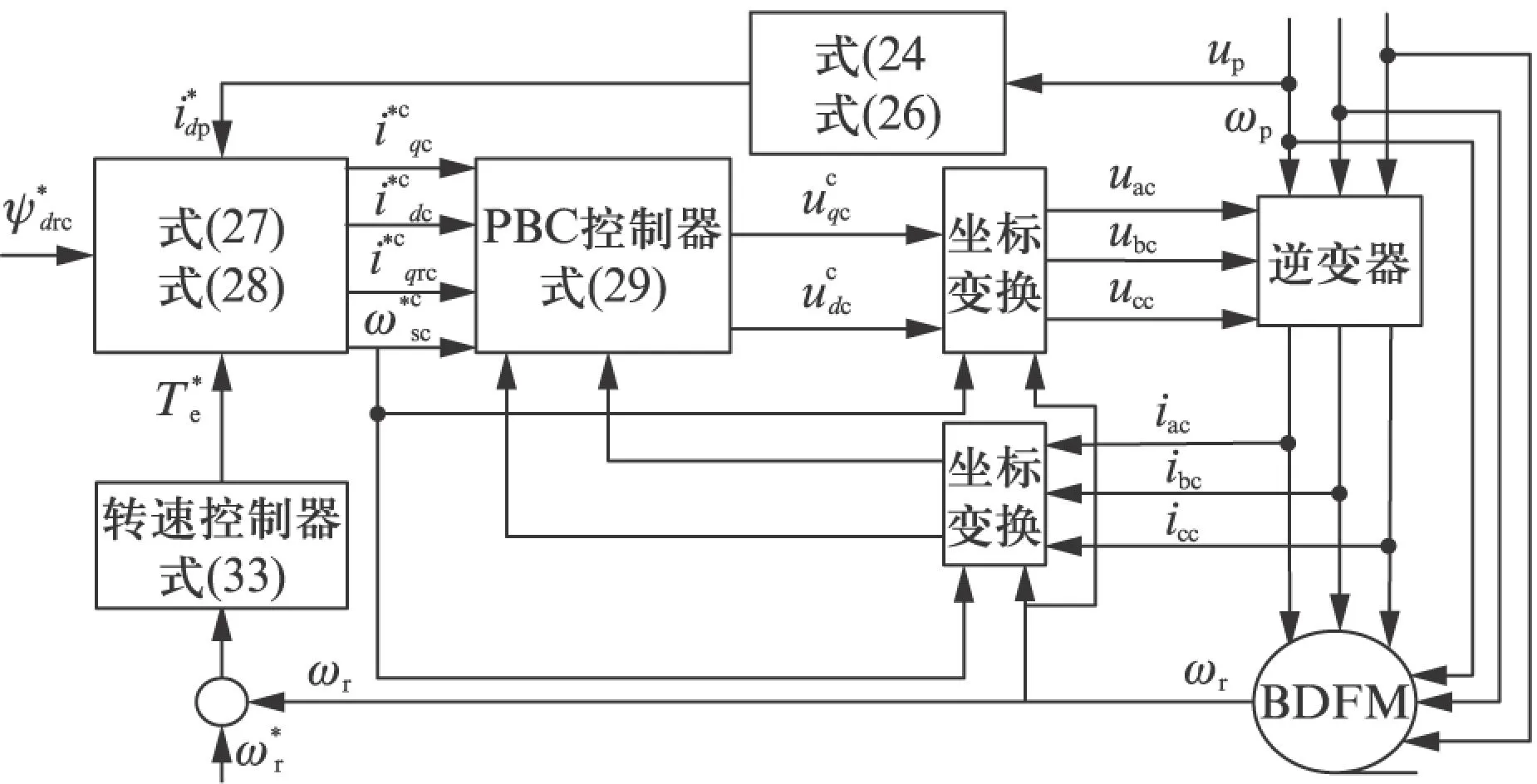
圖2　BDFM的無源控制結構

3系統仿真試驗

在MATLAB/Simulink平臺上搭建系統的各個模塊，建立系統的仿真模型并進行仿真。系統參數如下：pp=3，pc=1，rp=0.43Ω，rc=0.436Ω，rr=1.63Ω,rrp=rrc=0.5Rr=0.815Ω，Lp=71.38mH，Lmpr=69.31mH，Lc=65.33mH，Lmcr=60.21mH，Lr=142.8mH，a=70，J=0.03kg·m2，kp=10，ki=0.03，δ=0.003。

圖3為BDFM的初始轉速給定為750r/min時，空載起動，系統在0.25s時達到穩定，在2.5s時加入負載10N·m突變系統的動態響應波形。負載變化時，系統轉速超調量超過設定值的20%，并伴隨小幅振蕩，輸出轉矩跟蹤迅速，在2.8s時系統重新達到穩定，整個過程中，轉速波動較小，無超調現象。

圖3　負載變化時動態響應

圖4為BDFM初始轉速給定為600r/min時，轉速出現超調現象，系統經過0.3s的小幅振蕩后達到穩定，在2.5s時轉速給定突增到900r/min的動態響應波形。由圖4可見，轉速動態響應迅速，最大超調量不超過設定值的10%，在2.8s時系統達到電磁轉矩平穩。

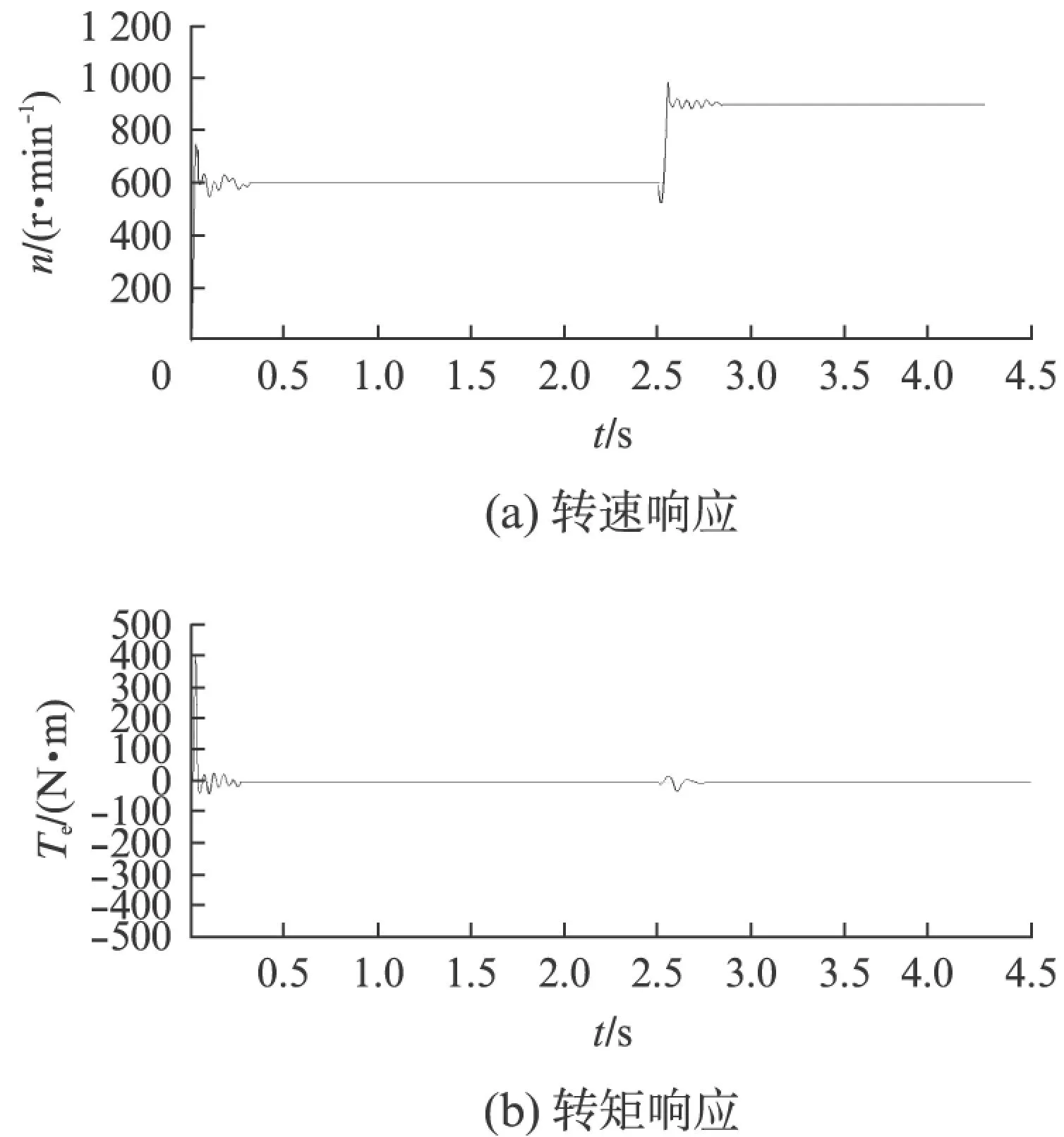
圖4　轉速變化時動態響應

4結語

在籠型轉子BDFM的轉速控制中引入無源性非線性控制方法，從能量的角度分離出系統“無功力”，有效簡化控制器設計，提高了系統魯棒性。以變結構的形式注入非線性阻尼，提高了系統收斂速度，改善系統動態響應。仿真結果驗證了方法的可行性。

【參考文獻】

[1]LI R,WALLACE A, SPEE R.Dynamic simulation of brushless doubly-fed machines[J]. IEEE Transactions on Energy Conversion, 1991,6(3)： 445-452.

[2]ZHOU D, SPEE R,ALEXANDER G C, et al. Experimental evaluation of a rotor flux oriented control algorithm for brushless doubly-fed machines[J]. Power Electronics, IEEE Transactions on Power Electronics, 1997,12(1)： 72-78.

[3]POZA J,OYARBIDE E, ROYE D.New vector control algorithm for brushless doubly-fed machines[C]∥Proceedings of the 28th IEEE Conference on Industrial Electrons Society Conference， Scvillc, Spain， 2002： 1138-1143.

[4]黃守道,王耀南,黃科元.無刷雙饋電機轉子磁場定向控制策略的研究[J].電工技術學報,2002, 17(2)： 34-39.

[5]劉曉鵬,張愛玲,樊雙英.無刷雙饋電機直接轉矩控制策略的研究[J].微特電機,2006,34(3)： 25-31.

[6]BRASSFILED W R, SPEE R, HABETLER T G.Direct torque control for doubly-fed machine[J].IEEE Transactions on Industry Applications, 1996,32(5)： 1098-1104.

[7]張愛玲,張洋.基于轉矩預測控制的無刷雙饋電機直接轉矩控制系統[J].電機與控制學報,2007, 11(4)： 326-330.

[8]SARASOLA I, POZA J, RODRIGUEZ M A, et al. Predictive direct torque control for brushless doubly fed machine with reduced torque ripple at constant switching frequency[C]∥The 2007 IEEE International Symposium on Indusfirial Elecfironics， Vigo, USA： IEEE, 2007： 1074-1079.

[9]JOVANOVIC M G, G DORRELL D. Sensorless control of brushless doubly-fed reluctance machines using an angular velocity observer[C] ∥The 7th International Conference on Power Electronics and DriveSystems, Piscataway, NJ： IEEE, 2007： 717-724.

[10]周欣欣,張愛玲.無刷雙饋電機直接轉矩控制轉矩脈動最小化[J].電機與控制學報,2006,10(6)： 571-575.

[11]蔡曉名,楊向宇.基于模糊PID的無刷雙饋電機矢量控制[J].微特電機,2005,33(11)： 30-32.

[12]郭紅霞,楊金明,劉文剛.無刷雙饋電機的PID神經網絡控制[J].控制理論與應用,2008,25(1)： 53-56.

[13]楊俊華,呂惠子,吳捷，等.基于波波夫超穩定性的無刷雙饋電機直接轉矩控制[J].中國電機工程學報,2009,29(15)： 107-113.

[14]ZHOU D, SPEE R, WALLACE A K.Model refer-ence adaptive speed control for doubly fed machines[C]∥Proceedings of the 19th Annual Conference of IEEE Indusfirial Elecfironics， New York, IEEE, 1993,2(2)： 1175-1180.

[15]楊俊華,李建華,吳捷，等.無刷雙饋風力發電機組的模糊自適應控制[J].電機與控制學報,2006,10(4)： 346-350.

[16]劉航航,韓力.無刷雙饋電機控制策略發展綜述[J].微特電機,2010(6)： 69-73.

[17]高勇,張文娟,楊媛,等.基于無源性的變速恒頻雙饋風力發電機控制系統[J].電工技術學報,2010,25(7)： 130-136.

[18]高勇,張文娟,楊媛，等.變速恒頻雙饋異步電機無源性控制[J].太陽能學報,2010,31(11)： 1491-1496.

[19]錢平,葛翔.雙饋感應風力發電機的無源性控制方法研究[J].太陽能學報,2009,30(11)1540-1545.

[20]呂惠子,楊俊華,吳捷，等.無刷雙饋調速電機無源性分析及自適應控制[J].控制理論與應用,2009,26(12)： 1425-1429.

[21]鄧先明.無刷雙饋電機的電磁分析與設計應用[M].北京： 機械工業出版社,2008.

[22]NICKLASSON P J, ORTEGA R, ESPINOS G P. Passivity-based control of a class of Blondel-Park transformable electric machines[J]. IEEE Transac-tions on Automatic Control, 1997,42(5)： 629-647.

[期刊榮譽]

中文核心期刊中國科技核心期刊中國學術期刊(光盤版)

全國優秀科技期刊華東優秀科技期刊

中國科學引文數據庫來源期刊中國學術期刊綜合評價數據庫來源期刊