基于聲振耦合的裝載機駕駛室多目標形貌優化設計

第一作者張俊紅女，博士，教授，博士生導師，1962年生

基于聲振耦合的裝載機駕駛室多目標形貌優化設計

張俊紅，李忠鵬，畢鳳榮，王鍵，朱傳峰

(天津大學內燃機燃燒學國家重點實驗室，天津300072)

摘要：對某裝載機駕駛室及室內聲腔進行建模得到聲振耦合模型，通過SIMO法模態試驗驗證所建模型的準確性，測取懸置點激勵力并進行頻響分析及室內噪聲預測。結合耦合模態頻率和噪聲曲線峰值頻率確定關鍵優化頻率，在駕駛室的最大扭矩工況下進行靜力學分析，采用折衷規劃法和平均頻率法將駕駛室靜態整體剛度和多階關鍵頻率歸一為Euclidean距離的多目標函數，對駕駛室進行多目標形貌優化。結果表明：此優化方法在駕駛室結構優化上的應用綜合提高了結構整體剛度和多階關鍵固有頻率，避免了單頻優化時頻率震蕩現象，得到了優化目標的整體Pareto最優解，室內噪聲總聲壓級降低了3.03 dB。

關鍵詞：聲振耦合；折衷規劃法；平均頻率法；多目標形貌優化；低噪聲

基金項目：國家高技術研究發展計劃(863計劃)資助項目(2012AA1117064) 國家自然科學基金(10902024);教育部新世紀優秀人才支持計劃(NCET-11-0086) ;江蘇省自然科學基金(BK2010397);航空科學基金(20090869009);江蘇高校優勢學科建設工程資助項目(1105007001)

收稿日期：2014-01-28修改稿收到日期：2014-04-06

中圖分類號:TB535

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.07.007

Abstract:The model of a loader cab and its acoustic cavity was built to compose an acoustic-structural coupling model and was verified by SIMO mode test. The excited forces at suspension points were measured, then the frequency response analysis and the prediction of the cab interior noise were proceeded. The critical optimization frequencies were determined according to the coupling mode and the sound pressure level curve, and the static analysis was conducted. under the typical working condition of the cab. The combination of the compromise programming approach and the average frequency method was applied to the multi-objective topography optimization of the cab by merging the static stiffness and several critical dynamic frequencies as the objectives in a Euclidean distance’s multi-objective function. The result shows that the application of the method in the cab optimization can improve the static stiffness and the critical frequencies synthetically, avoiding the frequency oscillation phenomenon and getting the Pareto solution of the optimal objectives, and the overall sound pressure level in the cab is dropped by 3.03dB.

Multi-objective structural optimization design of loader cab considering acoustic-structural coupling

ZHANGJun-hong,LIZhong-peng,BIFeng-rong,WANGJian,ZHUChuan-feng(State Key Laboratory of Engines，Tianjin University，Tianjin 300072,China)

Key words:acoustic-structural coupling; compromise programming approach; average frequency method; multi-objective topography optimization; low noise

裝載機作為一種廣泛應用的工程機械,其駕駛室室內聲場環境的優劣越來越受到人們的重視。由于其發動機功率高，振動大，導致駕駛室室內噪聲較高，降低室內噪聲對改善人機環境有較大意義。

更精確的模態分析在建模時有重要意義，在模態分析研究中，考慮聲壓作用的聲振耦合模態比不考慮聲壓的結構模態更貼近實際，國內外許多學者對駕駛室聲振耦合特性進行了研究。Gladwell等[1]用余能定理和Hamilton變分原理推導出了薄膜振動與聲振耦合理論表達式，為使用有限元法求解聲振耦合問題奠定了理論基礎。目前，國內外在聲振耦合振動分析的理論及應用方面發展較快[2-6]，尤其在理論研究方面日漸成熟，但是，在聲振耦合模態分析的基礎上進行恰當的結構優化有待進一步拓展研究。

形貌優化是結構優化設計的一種重要形式，是一種形狀最優化的設計方法。Marburg[7]利用單目標形貌優化對駕駛室地板進行了改進，使駕駛員右耳處聲壓降低了2 dB。舒歌群等[8]以提高油底殼的一階固有頻率為目標進行形貌優化，提高了油底殼前幾階固有頻率。張俊紅等[9]以柴油機機體裙部水平方向彎曲剛度為目標，運用形貌優化對柴油機機體進行了低振動設計。郝志勇等[10]以提高油底殼某階固有頻率為目標對油底殼進行了形貌優化。由于形貌優化肋板分布形式多樣，使其在板件優化研究中發展迅速[11-13]。吳軍潔等[14]基于拓撲優化和形貌優化，將多工況多目標函數線性加權為單目標函數，對駕駛室結構進行了多工況優化設計。但采用傳統的線性加權法進行多目標優化時，不能確保得到所有的Pareto最優解，若采用折衷規劃法可使所有特征值與目標值之間歐式距離最小化，得到Pareto最優解[15]。同時，平均頻率法可綜合提高各目標頻率值，有效防止單頻優化時出現的頻率振蕩現象。

本文在聲振耦合模態分析的基礎上，采用帶權重的折衷規劃法和平均頻率法相結合，對某裝載機駕駛室進行了多目標形貌優化，使得多階關鍵頻率定位更加精確，與采用線性加權法優化相比，可得到剛度和目標頻率的整體最優解，降低了室內噪聲聲壓級。

1聲振耦合及多目標形貌優化理論

1.1聲振耦合理論

聲振耦合系統中，箱體內部空腔聲場離散形式的波動方程為：

(1)

考慮聲壓對箱體振動作用時，結構振動控制方程為：

式中：[Ms]為結構質量矩陣；[Cs]為結構阻尼矩陣；[Ks]為結構剛度矩陣；{u}為結構位移矢量矩陣；{Fs}為結構外激勵矩陣。{Ff}表示耦合界面上的流體壓力載荷向量。方程(1)和方程(2)描述了聲-結構耦合系統的運動方程，由于{Ff}=RT{p},用統一矩陣的形式可以表示如下:

(3)

1.2折衷規劃法

對于非凸優化問題，線性加權法不能得到整體Pareto最優解，若采用折衷規劃公式可綜合考慮各子目標函數,使目標函數綜合最優。本文以駕駛室整體靜態結構柔度最小化為目標，其多工況下的折衷規劃目標函數可表示為:

(4)

式中：C代表結構柔度；M代表工況數目；p為懲罰因子；wk為第k個工況的權重系數；Ck為第k個工況的柔度最優解；Cmink為第k個工況的柔度目標函數最小值；Cmaxk為第k個工況優化迭代初始步的最大值。

1.3平均頻率法

單頻優化旨在提高某階固有頻率以避免結構發生共振，但實際工程中，許多結構存在多階振動明顯的模態，而且這些模態密集，若采用單頻優化，往往出現某階頻率達到最大，而與其相鄰階次的頻率卻降到一個較低的值，并且可能發生幾階頻率次序調換的頻率振蕩現象[13]。為避免此現象，可采用平均頻率公式建立多頻目標函數，綜合考慮多階關鍵頻率，其形式表示為：

(5)

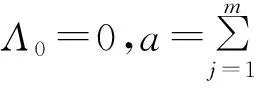
1.4多目標形貌優化理論

為綜合考慮整體結構剛度及多階模態特征頻率的影響，采用折衷規劃法和平均頻率法，將多目標形貌優化數學模型表示為：

(6)

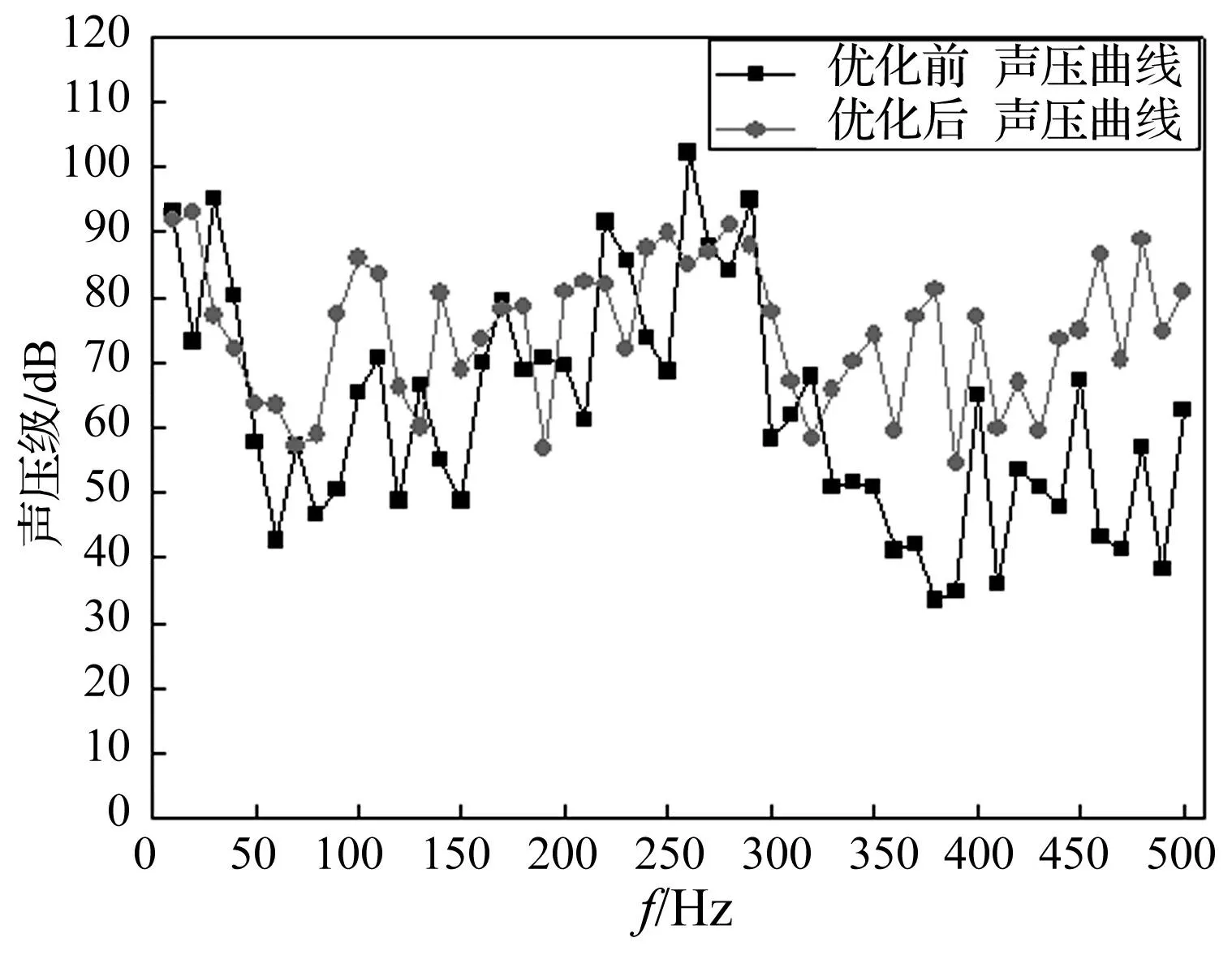
當1

(7)

2耦合模態分析及虛擬噪聲預測

2.1模型建立及模態驗證

某裝載機駕駛室主要由梁、柱、板(鋼板和玻璃)組成，建模時由于其實際結構復雜,故對其影響較小的孔、翻邊進行簡化，車窗和車身為剛性連接。在建立駕駛室模型的同時建立室內聲腔三維實體模型，并進行網格劃分。

駕駛室有限元模型長1 480 mm，寬1 300 mm，高1 570 mm，材料由鋼和玻璃構成，有限元網格由梁單元和殼單元組成，共36 044個節點，37 228個單元，室內聲腔網格共121 481個節點，86 381個單元，有限元模型如圖1所示。

圖1　駕駛室聲固耦合有限元模型 Fig.1 Acoustic-structural coupling FEA model of cab

模態試驗采用TEST.LAB測試系統，試驗采用錘擊法和SIMO測試法，采集得到的信號傳入DASP測試分析系統，并利用計算機進行處理。試驗測得的模態頻率與聲振耦合模態計算值之間的對比結果如表1所示。

表1　耦合模態計算值和試驗模態值對比

計算耦合模態時與試驗模態測試的邊界條件相同，均采用自由邊界條件。通過上表對比發現，試驗模態的結果與耦合模態計算值的相對誤差均不超過10%，表明所建立的有限元模型具有較高的精度，可進行下一步的分析計算。

2.2頻響分析及噪聲預測

駕駛室懸置系統減振方式為橡膠塊減振，由四個懸置點支撐,仿真時采用Rbe2梁單元模擬，均采用全自由度約束。測取懸置點激勵信號的工況為裝載機鏟斗滿載升至最高處且發動機轉速升至額定轉速2 200 r/min,對四個支撐點懸置后的加速度信號進行測取，懸置點激勵信號的實測圖如圖2所示。

圖2　懸置點激勵信號實測圖 Fig.2 Excited force test of suspension point

圖3　頻率為50 Hz時駕駛室振動響應云圖 Fig.3 Thecloud picture of cab vibration response at 50 Hz

將設置好輸入激勵的有限元模型導入Nastran中進行頻率響應分析求解，可得到各頻率下的振動響應及駕駛室各點的頻率響應振動幅值，其中頻率為50 Hz時的駕駛室振動響應云圖如圖3所示。

圖4　人耳處聲壓預測曲線 Fig.4 The predicted sound pressurelevel curve near the driver’s ear

將計算得到的駕駛室頻率響應數據導入LMS Virtual.Lab對駕駛員人耳處的聲壓級進行虛擬預測，如圖5所示。由于駕駛室室內噪聲由板件振動及輻射噪聲共同作用,其中壁板振動主要產生中低頻段噪聲,同時壁板附有多孔吸聲材料，其吸聲性能一般從低頻到高頻逐漸增大，故對中頻和高頻的吸收效果較好，對室內中高頻噪聲具有較強的降噪能力，因此對駕駛室結構優化的目標頻率取0 Hz~500 Hz,進行中低頻噪聲虛擬預測,其聲壓預測圖如圖4所示，計算得到總聲壓級為104.55 dB。

從上圖可以看出，關鍵峰值頻率分別為25 Hz、220 Hz、260 Hz、290 Hz，比其它峰值高出5 dB以上，其中在25 Hz處聲壓級超過了90 dB，在220 Hz、290 Hz和280 Hz三個頻率處聲壓級在90 dB-105 dB之間，同時通過查看激勵力信號可以發現，激勵力大約在220 Hz、260 Hz和290 Hz處峰值較高, 因此須找到25 Hz、220 Hz、260 Hz、290 Hz對應的模態頻率進行優化。結合耦合模態頻率，峰值頻率25 Hz、220 Hz、260 Hz、290 Hz分別對應耦合模態頻率的24.52 Hz、220 Hz、261.8 Hz、291.2 Hz，故將此四階約束模態頻率作為目標頻率進行優化，通過提高這四階關鍵模態頻率避免共振的發生，降低室內噪聲聲壓級。

3駕駛室多目標形貌優化

采用折衷規劃和平均頻率法進行多目標形貌優化時,需首先確定各工況柔度和頻率優化的最優值。裝載機工作時，當鏟斗滿載升至最高處時車架受到彎扭力矩最大，駕駛室也受到彎扭作用，故將此工況作為駕駛室工作的典型工況。在此工況下，以前輪為支撐點，受到后部車身重力的影響，在后懸置點處施加大小為5 000 N，方向垂直于地板的力模擬彎扭變形[16]，并進行靜力學分析。

利用HyperWorks軟件分別以典型工況下結構柔度最小化，四階關鍵模態頻率最大化為目標，進行單目標形貌優化，得到各單目標優化最優解。考慮到駕駛室實際安裝要求及懸置點的特殊位置，故將玻璃、梁單元與殼單元連接處和懸置點處設置為不可設計區域。將設計區域內的肋板屬性設為約束條件,定義起肋寬度為80 mm，斜度為60°，起肋高度為15 mm，得到優化后的各目標最優值如下表2所示。

表2　優化前后各參數目標值對比

通過Optimization卡片定義折衷規劃法和平均頻率法結合的多目標函數，其多目標優化函數為：

(8)

圖5　優化后肋板分布云圖 Fig.5 The cloud picture ofthe rib distribution after optimization

此外，采用線性加權法將柔度及頻率加權為單目標函數,對模型進行單目標形貌優化，與采用折衷規劃和平均頻率法結合的優化結果進行對比，如下表3所示。

表3　線性加權與折衷規劃法優化參數對比

通過上表對比發現，采用帶權重的折衷規劃法和平均頻率法可綜合提高結構剛度及各頻率目標值，f1由24.52 Hz提高到47.35 Hz，f2由220 Hz提高到383.5 Hz，分別提高93和74個百分點，采用線性加權法f1由24.52 Hz提高到42.04 Hz，f2由220 Hz提高到370.1 Hz，分別提高約71和68個百分點，比折衷規劃法分別低22和6個百分點。雖然線性加權法相比較折衷規劃法對柔度、f3、f4等參數有所提高，分別提高約0.3、0.7和1.2個百分點，但遠小于折衷規劃法對f1、f2的提高倍數，故其影響不大。可見，線性加權法雖能提高柔度和f3、f4等目標值，但不能大幅提高f1、f2的值，沒有得到整體最優解，與線性加權法相比，帶權重的折衷規劃和平均頻率法結合更能有效得到各目標值整體最優，體現整體最優解思想。

圖6　優化修正后三維模型 Fig.6 Themodified three-dimensional model after optimization

由于優化后形狀不規則，將優化后結果導出并進行部分修正，其駕駛室模型如圖6所示。

在此模型中施加相同的邊界條件與激勵力信號，進行頻響分析及室內噪聲二次預測，得到駕駛室優化前后室內聲壓預測曲線，如圖7所示。

圖7　駕駛室優化前后聲壓曲線對比 Fig.7 The comparison of the sound pressure level curve before and after optimization

由于此形貌優化旨在降低關鍵頻率峰值，通過對比聲壓曲線可以發現，優化后聲壓曲線峰值在各關鍵頻率處均得到明顯降低,表明結構優化有效。雖在350 Hz~500 Hz頻段內聲壓級有所提高,分析是由于提高駕駛室剛度所致，但計算得到的總聲壓級減小,總聲壓級由104.55 dB降低到101.52 dB，下降了3.03 dB,表明優化效果理想。

4結論

采用帶權重的折衷規劃法和平均頻率法，對某駕駛室聲振耦合模型進行了多目標形貌優化，綜合提高了駕駛室整體結構剛度和四階關鍵固有頻率，相比線性加權法可得到優化目標的整體Pareto最優解，對優化后的模型進行了聲壓二次預測，人耳處的總聲壓級整體降低了3.03 dB。

參考文獻

[1]Gladwell G M L, Zimmermann G. On energy and complementary energy formulations of acoustic and structural vibration problem[J]. Journal of Sound and Vibration, 1966,3(3): 233-241.

[2]Sun S H, Nefske D J.A coupled structural-acoustic finite element model for vehicle interior noise analysis[J]. Journal of Vibration Acoustics Stress and Reliability in Design, 1984, 106: 314-318.

[3]劉禹，喻凡，柳江.車輛乘坐室聲固耦合模態分析[J].噪聲與振動控制，2005，8:38-40.

LIU Yu, YU Fan, LIU Jiang. Modal analysis of vehicle compartment with acoustic-structure coupling[J]. Journal of Noise and Vibration Contral, 2005，8:38-40.

[4]惠巍，劉更，吳立言.轎車聲固耦合低頻噪聲有限元分析[J].汽車工程,2006,28(12):1070-1073.

HUI Wei, LIU Geng, WU Li-yan. Finite element analysis on the car interior low-frequency noise with acoustic-structural coupling[J].Journal of Automotive Engineering, 2006, 28(12):1070-1073.

[5]劉鵬，劉更，惠巍.駕駛室結構振動及其聲固耦合噪聲響應分析[J].機械科學與技術，2006,25(7)：856-859.

LIU Peng, LIU Geng, HUI Wei. Analysis of cab structure vibration and its acoustic coupling noise response[J]. Journal of Mechanical Science and Technology,2006,25(7)：856-859.

[6]舒磊，方宗德，趙冠軍.駕駛室結構減振降噪的拓撲優化設計[J].振動與沖擊，2008,27(3)：113-116.

SHU Lei, FANG Zong-de, ZHAO Guan-jun. Topology optimization design for noise reduction in a truck cab interior[J]. Journal of Mechanical Science and Technology, 2008,27(3)：113-116.

[7]Marburg S. A general concept for design modification of shell meshes in structural-acoustic optimization-Part Ⅱ: Application to a floor panel in sedan interior noise problems[J]. Finite Elements in Analysis and Design, 2002, 38(8):737-754.

[8]舒歌群,劉俊棟,李民，等.基于HyperWorks的柴油機油底殼有限元建模和結構優化[J].小型內燃機與摩托車,2008,37(1):25-27.

SHU Ge-qun, LIU Jun-dong, LI Min, et al. Building FEM model and structural optimization for oil pan on hyperworks[J].Journal of Small Internal Combustion Engine and motorcycle, 2008,37(1):25-27.

[9]畢鳳榮，杜憲峰，張俊紅，等.基于形貌優化的低振動柴油機機體設計[J].內燃機學報，2010,28(5)：459-463.

BI Feng-rong, DU Xian-feng, ZHANG Jun-hong, et al. Blockdesign of diesel engine for low vibration based on topography optimization[J]. Journal of Transactions of CSICE, 2010,28(5)：459-463.

[10]王奇文，郝志勇，李一民，等.基于FEM和BEM的低噪聲油底殼設計研究[J]．汽車工程，2013,35(4):364-368.

WANG Qi-wen, HAO Zhi-yong, LI Yi-min, et al. A research on the design of low- noise Oil-pan based on FEM and BEM[J]. Journal of Automotive Engineering. 2013, 35(4): 364-368.

[11]Min S, Nishiwaki S, Kikuchi N. Unified topology design of static and vibrating structures using multi-objective optimization[J].Computers and Structures,2000,75(1): 93-116．

[12]Ma Z D, Cheng H C, Kikuchi N, et al. Topology and shape optimization technique for structural dynamic problems[J].Journal of Recent Advances in Structural Problems,1992,248(10): 133-143．

[13]Ma Z D，Kikuchi N，Cheng H C. Topological design for vibrating structures[J]． Computer Methods in Applied Mechanics and Engineering,1995，121(4): 259-280．

[14]吳軍杰，陳靖芯，秦永法.基于拓撲和形貌優化的駕駛室結構設計[J].計算機輔助工程，2010,19(4)：62-65.

WU Jun-jie, CHEN Jing-xin, QIN Yong-fa. Structure design of vehicle cab based on topology and topography optimization[J].Journal of Computer Aided Engineering, 2010,19(4)：62-65.

[15]劉林華，辛勇，汪偉.基于折衷規劃的車架結構多目標拓撲優化設計[J].機械科學與技術,2009,30(3):382-385.

LIU Lin-hua, XIN Yong, WANG Wei. Multi-objective topology optimization for an off-road vehicle frame based on compromise programming[J]. Journal of Mechanical Science and Technology, 2009,30(3):382-385.

[16]韓明，吳曉明，黃鶴艇.多種工況下裝載機機罩多目標拓撲優化設計[J].廈門大學學報，2011,50(1)：56-59.

HAN Ming, WU Xiao-ming, HUANG He-ting. Multi-objective topology optimization of the loader hood with multiple loading conditions[J]. Journal of Xiamen University,2011,50(1)：56-59.