凹面光柵分辨率的檢測方法研究

蘇仰慶　黃元申　楊海馬

摘要：構建滿足凹面光柵使用條件的精確檢測系統來檢測凹面光柵的分辨率，根據系統的光源帶寬、狹縫寬度和探測器像素尺寸的理論分析，結合凹面光柵的像差分析，給出一種凹面光柵分辨率檢測系統的檢測方法。系統按照JB/T 8239.2—95《衍射光柵技術條件》的標準方法，定量分析出上述三個因素的影響量，并提出了合理的計算方法，從而在檢測系統的測量值中得到了凹面光柵實際的分辨率值。通過實驗驗證，實際檢測結果與理論分析結果相差0.001 0～0.003 7 nm，是一種能夠真實反映凹面光柵分辨率的光學檢測方法。

關鍵詞：凹面光柵； 分辨率； 光源帶寬； 狹縫寬度； 像素尺寸

中圖分類號： TH 744.1 文獻標志碼： A doi： 10.3969/j.issn.10055630.2015.06.006

Abstract：In order to detect the resolution of the concave gratings， it needs to build a precise detection system. Based on the theoretical analysis of the system of the bandwidth of light source， the slit width and the pixel size of the detector， combining with the aberration analysis of concave gratings， a method for the resolution detection system is proposed. According to the standard method in JB/T 8239.2-95 which is named The technical conditions for diffraction grating， the system analyzes the above three factors quantitatively and puts forward a reasonable calculation method. Then it can obtain the practical value of concave grating resolution in the detection system. By experimental verification， the method can distinguish the difference between the test results and the theoretical analysis results from 0.001 0 nm to 0.003 7 nm.

Keywords：concave grating； resolution； light source bandwidth； slit width； pixel size

引 言

凹面光柵既是色散元件，又是成像系統，構成的光學系統更簡單，在光譜儀中應用也更為廣泛。分辨率是光譜儀最重要的指標之一，因此在裝調前需要對凹面光柵進行檢測[1]。凹面光柵的使用條件不同于平面光柵，其入射波和衍射波均為球面波，入射角度、入臂和出臂的長度，即光柵、入縫和探測器三者的位置，是經過消像差設計得出的[2]，不可隨意放置。這給凹面光柵的檢測帶來困難，要根據不同凹面光柵的使用參數來構建檢測系統。雖然現有的光學系統設計軟件采用光線追跡法，根據點列圖或對比傳遞函數MTF來評估系統的分辨率，但是由于制造安裝的誤差，實際分辨率要低于理論值。目前，文獻中有關于凹面光柵衍射效率的理論計算研究的[34]，也有較多文獻關注對影響凹面光柵分辨率的因素進行理論分析的，而對于分辨率檢測方法的理論與實驗進行綜合分析研究，得出真正凹面光柵分辨率而非帶入系統影響因素的研究還沒有具體文獻。若僅從縫光源寬度、光柵寬度及入縫寬度與分辨率的關系做定性研究，分析光柵實際分辨率恒小于理想分辨率的結論，并沒有深入具體考慮整個分辨率檢測系統各個因素對分辨率的綜合影響，具有局限性[57]。本文主要定量分析了檢測系統中光源帶寬、狹縫寬度及探測器各個參數對分辨率的影響，結合羅蘭型凹面光柵的成像特點，計算寬波段使用范圍內的凹面光柵實際分辨率。

1 影響凹面光柵分辨率檢測的因素

要檢測一塊凹面光柵的分辨率，必須構建符合此光柵使用條件的檢測系統，而檢測系統的光源、狹縫和探測器以及其放置位置的精度不可避免地影響光柵檢測結果。因此為了得到真正的凹面光柵分辯率必須對這些影響因素加以科學的分析，并在檢測數據里，合理地加以去除。

凹面光柵的分辨率是指以點或線單色光源入射時，在像面上按照瑞利準則可分辨的最小光譜范圍。在實際檢測中沒有這種光源，總是帶有一定的尺寸大小和光譜帶寬，因此應考慮它們對分辨率的影響。檢測系統的光源采用標準汞燈，檢測波段為200～1 000 nm。汞燈出光用光纖耦合，用聚光透鏡將光斑聚焦在狹縫中心上，以近似點光源發散球面波入射到凹面光柵表面。必須注意的是入射光經光柵衍射的特征譜線事實上有一定的帶寬；狹縫上的聚焦光點也有一定的尺寸大小；經過狹縫的入射球面波必須充滿整個光柵表面，才能正確檢測出光柵的光譜分辨本領。

1.1 光源帶寬對分辨率檢測的影響

如圖1所示，假設入射單色光波長λ存在一個很小的譜線帶寬為δλ，入射角為α，衍射角為β。在不考慮像差時光柵理論最小可分辨角為Δβ=λNecosβ，其中N為總刻線數，e為有效刻線數。如果考慮像差，則其主極大的半波光譜寬度為ΔλG=λkN+δdλdl[8]，其中δ為像差斑的半徑，k為衍射級次。這就是要檢測的凹面光柵的光譜分辨率。由于光源的非單色性，檢測到的光譜半波寬度為（ΔλG+δλ），因此在檢測的數據中要剔除量δλ。

實驗中采用的低壓汞燈是氣體放電光源，其原子譜線并非一條嚴格的幾何線，無論是發射線還是吸收線，都具有一定的形狀，即譜線輪廓。譜線的強度隨頻率的改變而改變，定義v2v1的值Δv0為頻譜寬度，如圖2所示。

假設光波的波列長度為2 L，則由傅里葉頻譜分析可知單色光λ的譜線寬度與波列長度的關系為δλ=λ22L。低壓汞燈的蒸汽壓只有1.3～13 Pa，其譜線增寬主要是多普勒增寬，譜寬為δλ=2λc2KTln2m，其中c為光速，K為波爾茲曼常數，T為熱力學溫度，m為原子或分子的質量[9]。低壓汞燈譜線在300 K時的理論多普勒增寬如表1所示。

1.2 狹縫寬度對光柵分辨率檢測的影響

理想的點線光源是不存在的，要給光柵一定的光通量，那么狹縫一定要有大小。系統分辨率雖然隨狹縫寬度調小而變高，測的光柵分辨率也越精確，但由于檢測的光能量太小，信噪比低，這樣就降低了測量的靈敏度，同時也降低測量的正確性。因此需要同時考慮光源和探測器的性能以及被測光柵的特性選擇一個合理的狹縫寬度。如圖3所示，若入射狹縫的寬度為A1A2=a，其波長為λ的衍射像為B1B2=b，則光柵的衍射像b=rBcosαrAcosβ·a，其對于檢測帶來的分辨率降低的理論影響值為b/2線寬度對應的光譜寬度。應用色散公式可以計算出狹縫寬度在光柵檢測中帶入的光譜展寬ΔλA=aecosα2KrA，因此在實際測量值中要減去該值。

選定波長為435.8 nm，通過調節狹縫的不同寬度來分析其對光柵分辨率檢測的影響。圖4分別是狹縫寬度為5 μm、10 μm、50 μm、100 μm時檢測結果對照圖。從實驗結果可以看出，不同狹縫寬度對檢測結果影響很大。狹縫寬度a=5 μm時，Δλ=0.016 5 nm；a=10 μm時，Δλ=0.017 7 nm；a=50 μm時，Δλ=0.021 0 nm；a=100 μm時，Δλ=0.025 1 nm。減小狹縫寬度有利于提高系統的分辨率，但是隨著狹縫寬度的減小，會使光強迅速減弱。因此，在不影響光強的前提下應盡可能地減小狹縫寬度，決定系統的最佳光譜帶寬。過分減小狹縫寬度，光強急劇減弱且檢測結果不符合光柵實際分辨率值。通過實驗數據對比，在狹縫寬度為10 μm時，檢測光強值最合適，檢測數值也最接近光柵實際分辨率值，對應的ΔλA如表2所示。

假設被測光柵的參數值是：空間頻率1/e=2 400 l/mm，入臂長度rA=292.098 mm，檢測波長λ=435.8 nm，出臂長度rB=373.8 mm，狹縫寬度a=10 μm。計算狹縫寬度對光柵分辨率檢測影響的光譜寬度為ΔλA=0.009 7 nm。實際測量值為Δλ=0.017 7 nm，低壓汞燈435.8 nm譜線在300 K時的多普勒增寬為δλ=0.000 38 nm，則可見光柵的實際分辨率為Δλr=0.007 6 nm。

1.3 CCD探測器對光柵分辨率檢測的影響

因為狹縫經凹面光柵衍射后在像面上成二維光譜像，所以根據光路結構要求，為了采集到高質量的光譜像，選擇面陣CCD放置于像面上采集圖像。每個像素采集到的光能量用對應積累的電荷量來記錄并轉換成電壓，經A/D轉換后用數字信號輸出，此時CCD能夠分辨的最高空間頻率等于它的空間采樣頻率f0的一半，也就是光譜像在CCD的感光面上至少占兩個像素。CCD的光譜分辨本領是由像素尺寸和系統的線色散率決定的。假設兩個相鄰像素點中心間距為p，系統的線色散率表示為dldλ，CCD可分辨最小波長差ΔλC=2pdλdl，則CCD的光譜分辨率本領為RC=λΔλC=λ2p·dldλ，由此可見CCD的光譜分辨本領與像素間距p成反比[9]。另一方面，CCD采樣信號的過程與曝光時間和增益有關，曝光時間和增益過大會導致感光面采集到的光強太強，超出像素滿阱容量，像素中的電子會溢出，從而影響相鄰像素點的探測采集；曝光時間和增益過小會導致感光面采集到的光強太弱，像素點積累的電荷量無法反應實際的入射光能量，所以CCD存在一個曝光時間和增益的最合適值問題。

曝光時間從8 000～2 000 ns減小，增益從32～18減小時，實驗檢測的像素點隨曝光時間的減小而減小。同一曝光時間不同增益情況下，像素點有最佳值，當增益達到一定下限時，像素點也達到了極限數值；同一增益不同曝光時間情況下，當曝光時間達到一定下限時，像素點也有極限數值。根據實驗數據，本系統曝光時間為7 000 ns，增益為23時是CCD的最佳探測模式，光強適中，像素點最合適采集到的分辨率曲線最適合數據分析。

2 實 例

針對上述的實驗研究，利用CodeV光學設計軟件，根據凹面光柵的設計要求，在寬波段模擬了羅蘭圓型凹面光柵的成像系統。其光柵參數為曲率半徑400.7 mm，刻線數1/e=2 400 l/mm，入射角α=-43.2°，有效口徑為32 mm。凹面光柵分光光路的參數如表3所示。

可得到仿真光路如圖5所示，入射光經光柵分光后在像面從上往下依次分布分別為579.0 nm、577.0 nm、546.1 nm、435.8nm、404.7 nm和365.0 nm的衍射光譜像，優化前生成的MTF曲線見圖6，相應波長的均方根直徑RMS值如表4所示。

RMS值是一個重要的直徑參數，它是彌散斑各個點坐標與參考中心點進行坐標平方和后，除以點數量后再開方的值。該值可以典型地反映一個彌散斑的大小，以定量地反映這個系統實際的斑點大小。

由以上可以看出凹面光柵在子午面和弧矢面的成像質量與極限值均有一定的差距，具有較大像差。由其初始結構并不能得到較好的成像質量，必須對凹面光柵進行消像差優化設計，減小像差。利用CodeV軟件優化，通過點列圖和MTF曲線對凹面光柵的成像質量進行評估。

優化后的結果如表5所示。

經過優化后凹面光柵的成像聚焦在像面上，如圖7所示；優化后的MTF曲線和理論極限值也較為接近，可以獲得高成像質量的凹面光柵，如圖8所示；優化后相應波長的RMS值如表6所示。

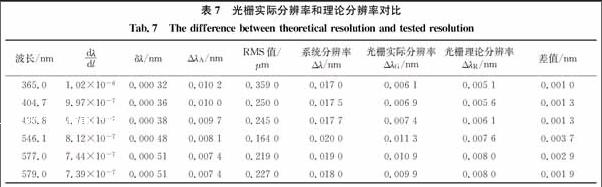
通過對比可以看出，在系統中綜合考慮光源帶寬、狹縫寬度及凹面光柵的像差后，檢測的光柵實際分辨率貼近于光柵理論分辨率，差值在0.001 0～0.003 7 nm之間，能夠真實反映光柵的實際分辨率，光柵實際分辨率和理論分辨率的差值如表7所示。

3 結 論

文章首先介紹了羅蘭圓型凹面光柵分辨率特性檢測系統的結構及工作原理，再根據實驗數據分析了光源帶寬、狹縫寬度、CCD曝光時間與增益及凹面光柵的像差對分辨率檢測結果造成的影響。不同光源具有不同的線性展寬，以汞燈作為標準光源，量化出擴展光源影響的理論數據。不同狹縫寬度對結果影響不同，通過實驗測試數據選取最佳狹縫寬度。考慮凹面光柵的像差并進行消像差優化設計，在系統中剔除像差對光柵實際分辨率的影響，CCD調節合適的曝光時間與增益，得到凹面光柵的實際分辨率數值，這對凹面光柵的制作有著重要的參考價值。

參考文獻：

[1]劉盛剛，翁繼東，陶天炯.超高分辨光譜儀的分辨率檢測方法研究[J].光譜學與光譜分析，2013，33（4）：903905.

[2]PI D Y，HUANG Y S，ZHANG D W，et al.Optimization of the flatfield holographic concave grating in wide spectral range[J].Acta Physica Sinica，2010，59（2）：1009 1016.

[3]HUANG Y S，LI T，XU B L，et al.Calculation of the diffraction efficiency on concave gratings based on FresnelKirchhoffs diffraction formula[J].Applied Optics，2013，52（5）：11101116.

[4]李亭，黃元申，徐邦聯，等.計算凹面閃耀光柵衍射效率的通用方法[J].光譜學與光譜分析，2013，33（7）：19972001.

[5]蔡履中.光源寬度對光柵分辨本領的影響[J].大學物理，1985，4（10）：2123.

[6]王永樂.光柵衍射試驗中光柵分辨本領的觀測[J].工科物理，1997（4）：4143.

[7]沈德洪.光柵分辨率測試裝置的設計[J].浙江大學學報，1985，19（6）：142147.

[8]HUTLEY M C.Diffraction gratings[M].New York：Academic Press，1982.

[9]祝紹箕，鄒海興，包學誠，等.衍射光柵[M].北京：機械工業出版社，1986.

[10]于常青，劉杰，李家澤，等.光學多通道分析儀的分辨率分析[J].光學技術，2001，27（2）：97102.

[11]嚴羚瑋.寬波段高分辨率Dyson成像光譜儀設計研究[J].光譜學與光譜分析，2014，34（4）：11351139.

[12]孔鵬，唐玉國，巴音賀希格，等.零像散寬波段平場全息凹面光柵的優化設計[J].光譜學與光譜分析，2012，32（2）：565569.

[13]裴梓任，黃元申，倪爭技.Offner 雙鏡三反射成像光譜儀分辨率的研究[J].光學儀器，2014，36（2）：147151

（編輯：程愛婕）