給分式方程應用題歸歸類
王康康


學習了分式方程的有關內容,同學們還必須得熟練運用分式方程解決實際生活中的問題.常見的實際問題有營銷類應用性問題、工程類應用性問題、行程類應用性問題等幾大類,這些題目看似復雜,但只要抓住“找等量關系、恰當設未知數、確定主要等量關系、用含未知數的分式或整式表示未知量”等關鍵環節,正確列出方程,再進行求解即可.不過同學們一定要注意的是,得出方程的解后,一要檢驗所求的解是否是原方程的解,二要檢驗所求的解是否符合題意,三要注意檢驗和解釋結果的合理性.
一、營銷類應用性問題
例1 某校辦工廠將總價值為2 000元的甲種原料與總價值為4 800元的乙種原料混合后,其單價比原甲種原料每斤少3元,比原乙種原料每斤多1元,問:混合后的原料每斤是多少元?
分析:市場經濟中,常遇到營銷類應用性問題,這類問題中與價格有關的量是單價、總價、平均價等,要了解它們各自的意義,從而建立它們之間的關系式.
解:設混合后的原料單價為每斤 [x]元,則原甲種原料的單價為每斤([x]+3)元,原乙種原料的單價為每斤([x]-1)元,混合后的總價值為(2 000+4 800)元, 混合后的重量為[2 000+4 800x]斤,甲種原料的重量為[2 000x+3]斤,乙種原料的重量為[4 800x-1]斤, 依題意,得
[2 000x+3]+[4 800x-1]=[4 800+2 000x]
解得
[x]=17
經檢驗,[x]=17是原方程的根.
所以[x]=17. 即混合后的原料每斤 17元.
總結:營銷類應用性問題,涉及進貨價、售貨價、利潤率、單價、混合價、贏利、虧損等概念,要結合實際問題對它們各自表述的意義有所了解.同時,要掌握好基本公式,巧妙建立關系式.這類問題與現實生活息息相關,因而成為中考常考的熱點問題.
【練習1】
A、B兩名采購員去同一家飼料公司購買同一種飼料兩次,兩次飼料的價格有變化.兩名采購員的購貨方式不同,其中采購員A每次購買1 000千克,采購員B每次用去800元而不管購買飼料多少,問:誰的購貨方式合算?為什么?
二、工程類應用性問題
例2 某工程由甲,乙兩隊合做6天完成,廠家需付甲,乙兩隊共8 700元;乙,丙兩隊合做10天完成,廠家需付乙,丙兩隊共9 500元;甲,丙兩隊合做5天完成全部工程的[23],廠家需付甲,丙兩隊共5 500元.
(1)求:甲,乙,丙各隊單獨完成全部工程各需多少天?
(2)若工期要求不超過15天完成全部工程,問:由哪個隊單獨完成此項工程花錢最少?請說明理由.
分析:這是一道聯系實際生活的工程應用題,涉及工期和工錢兩種未知量.對于工期,一般情況下把整個工作量看成1,設甲,乙,丙各隊完成這項工程所需時間分別為x天,y天,z天,可列出分式方程組.
解:(1)設甲隊單獨做需x天,乙隊單獨做需y天,丙隊單獨做需z天,依題意,得
[ 6([1x+1y])=1
10([1y]+[1z])=1
5([1x]+[1z])=[23] ]
[解得x=10y=15z=30]
經檢驗,[x]=10,[y]=15,[z]=30是原方程組的解.
(2)設甲隊做一天廠家需付a元,乙隊做一天廠家需付b元,丙隊做一天廠家需付c元,根據題意,得
[6(a+b)=8 70010(b+c)=9 5005(c+a)=5 500 ]
[解得a=800b=650c=300]
由(1)可知完成此工程不超過既定工期只有兩個隊:甲隊和乙隊.
此工程由甲隊單獨完成需花費10a=8 000元;此工程由乙隊單獨完成需花費15b=9 750元.
所以,由甲隊單獨完成此工程花錢最少.
技巧點撥:在(1)的求解時,把[1x],[1y],[1z]分別看成一個整體,可把分式方程組轉化為整式方程組來解.
【練習2】
某工程需在規定日期內完成,若由甲隊去做,恰好如期完成;若由乙隊去做,要超過規定日期3天才能完成.現由甲、乙兩隊合做2天,剩下的工程由乙隊獨做,恰好在規定日期內完成,問:規定的日期是多少天?
【練習3】
今年某大學在招生錄取時,為了防止數據輸入出錯,2 640名學生的成績數據由兩位教師分別向計算機輸入一遍,然后讓計算機比較兩人的輸入是否一致.已知教師甲的輸入速度是教師乙的2倍,結果甲比乙少用2小時輸完.問:這兩位教師每分鐘各能輸入多少名學生的成績?
三、濃度應用性問題
例3 有含鹽15%的鹽水40千克,要使鹽水含鹽20%,還需要加入多少千克鹽?
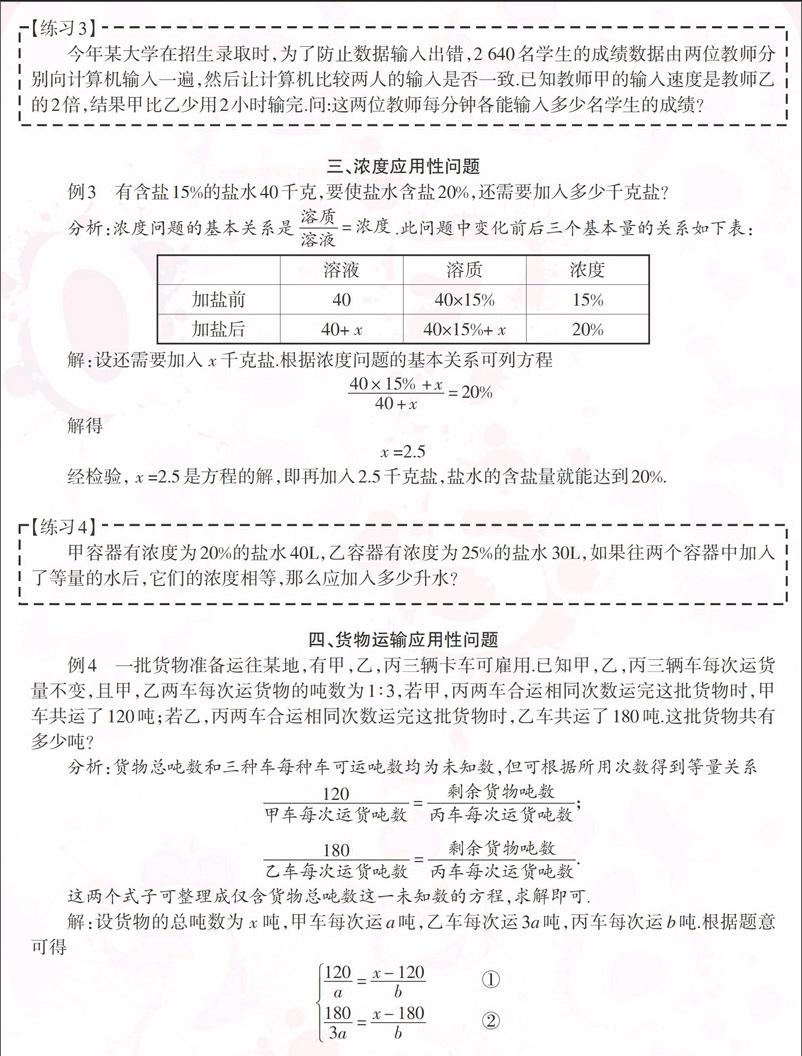
分析:濃度問題的基本關系是[溶質溶液=濃度].此問題中變化前后三個基本量的關系如下表:
[\&溶液\&溶質\&濃度\&加鹽前\&40\&40×15%\&15%\&加鹽后\&40+[x]\&40×15%+[x]\&20%\&]
解:設還需要加入[x]千克鹽.根據濃度問題的基本關系可列方程
[40×15%+x40+x=20%]
解得
[x]=2.5
經檢驗,[x]=2.5是方程的解,即再加入2.5千克鹽,鹽水的含鹽量就能達到20%.
【練習4】
甲容器有濃度為20%的鹽水40L,乙容器有濃度為25%的鹽水30L,如果往兩個容器中加入了等量的水后,它們的濃度相等,那么應加入多少升水?
四、貨物運輸應用性問題
例4 一批貨物準備運往某地,有甲,乙,丙三輛卡車可雇用.已知甲,乙,丙三輛車每次運貨量不變,且甲,乙兩車每次運貨物的噸數為1∶3,若甲,丙兩車合運相同次數運完這批貨物時,甲車共運了120噸;若乙,丙兩車合運相同次數運完這批貨物時,乙車共運了180噸.這批貨物共有多少噸?
分析:貨物總噸數和三種車每種車可運噸數均為未知數,但可根據所用次數得到等量關系
[120甲車每次運貨噸數=剩余貨物噸數丙車每次運貨噸數;]
[180乙車每次運貨噸數=剩余貨物噸數丙車每次運貨噸數.]
這兩個式子可整理成僅含貨物總噸數這一未知數的方程,求解即可.
解:設貨物的總噸數為[x]噸,甲車每次運a噸,乙車每次運3a噸,丙車每次運b噸.根據題意可得
[120a=x-120b ①1803a=x-180b ②]
解得
[x]=240
經檢驗,[x]=240是方程的解,即這批貨物共有240噸.
【練習5】
五、行程中的應用性問題

