一種認知MTD雷達脈間編碼設計方法

(南京航空航天大學電子信息工程學院,江蘇南京211106)

0 引言

對現代雷達而言,雜波中的目標檢測是最具挑戰的問題之一,因此一直以來雜波抑制都是雷達技術發展的重要推動力之一。雖然歷經幾十年的發展,動目標檢測(Moving Target Detecting,MTD)雷達系統在系統設計和工程實現方面均日趨成熟,部分系統的性能指標接近理論極限。但其所處的電磁環境日趨復雜,工作環境瞬息萬變。因此,如何針對MTD系統進行升級,進一步提高雜波環境下的檢測性能,提升系統的智能化水平,是雷達界目前關心的重要問題。

認知雷達(Cognitive Radar,CR)作為一種新型智能雷達系統[1-2],為未來雷達系統利用反饋信息設計自適應波形進行雜波抑制提供了一種新思路。目前對認知雷達雜波抑制波形設計研究主要從兩個角度開展。一是脈內編碼調制設計,這是目前研究比較成熟和集中的角度。針對雜波下的距離擴展目標檢測問題,以Pillai和Guerci[3-4]為代表的研究人員根據距離擴展目標的沖激響應及背景雜波和噪聲,提出了有限時寬信號的迭代設計方法,以最大化濾波器輸出的信雜噪比(Signal to Clutter and Noise Ratio,SCNR),通過在VHF波段下對T-72和M1坦克目標進行不同姿態角的照射實驗驗證了檢測性能的提升。二是脈間編碼設計,以De Maio為代表的研究人員以雜波和干擾環境下最大化SCNR為目標,在波形相似度等約束下提出了一系列的編碼設計方法[5-6];文獻[7]則在上述基礎之上,將模型拓展到信號相關雜波環境中,提出了兩種脈間編碼優化設計方法,即Co Re和CADCODE算法。

本文針對文獻[7]中兩種算法涉及矩陣求逆和分解等復雜操作、計算量大和難以實現實時處理的問題,研究一種新的脈間編碼設計方法。建立了信號相關雜波環境下的脈間編碼MTD雷達信號模型;分析了SCNR的改善機理并給出了脈沖編碼優化設計準則;基于加權冪平均不等式(Weighted Power Mean Inequality,WPMI)提出了非凸轉凸的優化問題轉化方法,并針對轉化后的錐約束下二次型規劃問題提出了一種基于簡約梯度的編碼設計方法;進行計算機數值仿真。

1 認知MTD雷達信號模型

1.1 脈間編碼回波信號模型

假設對某MTD雷達發射的N個脈沖信號進行脈間編碼,并對其接收到的回波信號進行正交解調和匹配濾波,在t=n TPRI+τ時刻(0≤n≤N-1)處抽樣得到離散回波信號[7]:

式中:TPRI表示脈沖重復周期,N表示發射信號的脈沖個數;α表示均值為0、方差為σ2T的復高斯隨機變量(對目標而言即Swerling-I模型);a=表示脈間編碼表示向量的轉置;目標多普勒頻率構成的多普勒矢量p=和n分別表示在回波中,與信號相關的雜波信號c(t)和噪聲n(t)經過正交解調、匹配濾波和抽樣后得到的離散矢量;表示哈達瑪乘積。由于這里的雜波為信號相關雜波,因此,脈間編碼的調制方式會體現在接收雜波中。

1.2 脈間編碼的可行性分析

利用式(1),動目標檢測的二元假設檢驗表示為

在已知目標信號多普勒頻率的情況下,根據最大似然比檢驗(Generalized Likelihood Ratio Test,GLRT),其最佳檢測器的性能是由SCNR來決定的[8]:

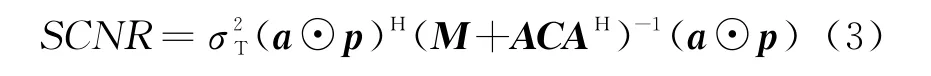
式中:(·)H表示矢量或矩陣的共軛轉置;A=diag(a),diag(·)表示矢量構成對角矩陣主對角線上的元素;C和M分別是c和n的協方差矩陣,可通過預先掃描或先驗知識獲得。

式(3)表明:經典的脈間無編碼發射方式,SCNR取決于協方差矩陣C和M;而在認知發射的方式下,SCNR則有可能通過脈間編碼a的調整,獲得無編碼發射方式基礎上性能的改善。此外,由于C和M一般用復數表示,因此,用于脈間編碼的矢量a亦可用復數(即脈間編碼同時體現在幅度和相位的調整)。

式(3)的另一種表示形式如下:

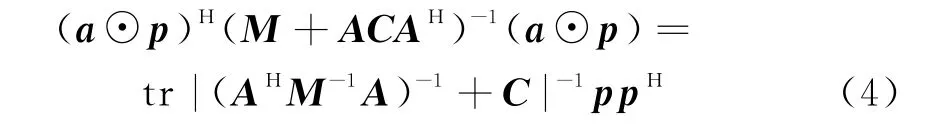
式中,tr(·)表示矩陣的跡。當M為對角矩陣(即白噪聲情況)時,AHM-1A只與a幅度值有關,與相位無關。因此,白噪聲情況下脈間編碼僅體現在a的幅度,而與相位無關。

2 基于WPMI的優化問題轉化

在限定發射能量的約束下,以SCNR最大化為設計準則,認知M TD雷達脈沖編碼設計的優化問題可表示為

式中,‖·‖2表示向量的2范數,e表示脈沖編碼的能量。由于式(5)中目標函數的強非凸性,增加了求解過程中的難度以及最優結果的多值性。

由于凸問題具有局部最優解是全局最優解、避免算法初始化、搜索步長選擇和陷入局部最優值的優點,同時具有高效求解算法的優勢。本文考慮將式(5)的非凸優化問題轉化為凸優化問題處理。

定理1:令S為正定矩陣,則存在以下不等式:

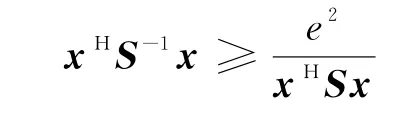
證明:根據 WPMI,有

得證。

因此,存在以下不等式:

式(6)表明式(5)中的非凸目標函數存在一個下確界(Inf)。通過下確界的提高可在一定程度上改善目標函數。由于下確界形式是一個明顯的凸函數,式(5)中非凸優化問題可表示為如下的凸優化問題:

即

式(8)成功地將非凸最大化問題向最小化凸問題進行轉化。需要注意的是,隨之而來的代價是目標函數中出現了四次型。因此,式(8)可歸結為二次約束四次型規劃優化問題(Quadratic Constrained Quartic Programming,QCQP)。該問題的求解仍較為復雜。

3 認知MTD雷達脈間編碼設計方法

3.1 白噪聲下的簡化問題

非白噪聲情況下噪聲協方差矩陣M的非對角化會在一定程度上帶來求解過程復雜。當噪聲為高斯白噪聲,上述優化問題將進一步簡化。

這里假設噪聲協方差矩陣表示為

3.2 脈間編碼優化問題

在傳統M TD雷達中,目標的多普勒頻率是未知的,相應的w也未知,在這種未知情況下,目標檢測的難度系數增加;然而對于認知M TD雷達,能通過關于目標的先驗知識和一些認知方法[1,9]粗略估計目標多普勒頻率w的范圍w l,w H和w的概率密度函數,并通常假設w在w l,w H的范圍內為均勻分布。針對上述情況,對簡化的目標函數式(10)作了如下推導:

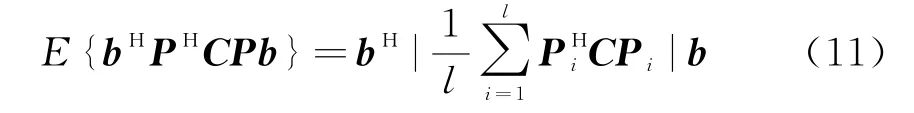
式中,E{·}表示求取期望,l表示目標離散多普勒頻率的個數,w i∈w l,w H,矩陣P i=diag(|1 ejwi…ej(N-1)wi|)。

式中,I N表示N×1的全1的列向量,0 N表示N×1的全為0的列向量。

注意到式(12)中的優化變量為實數,而矩陣G為復數,上述問題表示為

3.3 SGMCODE算法設計

簡約梯度法的基本思想是對于線性約束條件,通過降低變量維數將有約束的優化問題轉為無約束的優化問題;采用無約束的梯度法求解[10]。針對式(13)的優化問題具體的實現步驟如下:

Step1:通過求解線性約束中的方程組,將部分變量解出,經過消元處理,將有約束優化問題轉化為新的優化問題(降維)。將線性約束函數中系數向量和變量b,目標函數中的(G)進行如下分塊:

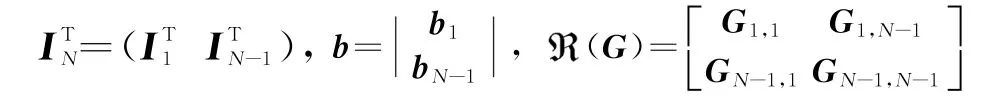
式中:I1為1階的單位向量,I N-1為(N-1)×1的全1向量;b1為1階的向量,b N-1為(N-1)×1的向量。

借助約束函數可以將b1用b N-1表示:

將分塊矩陣和式(14)代入式(13),優化問題轉化為

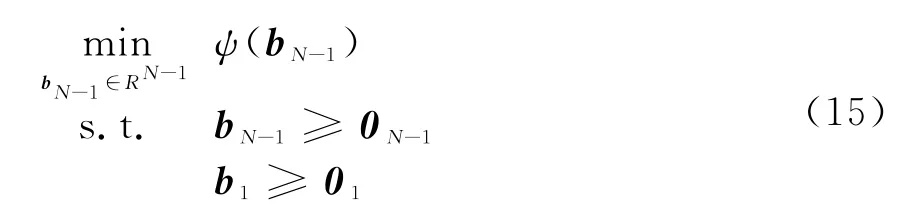
式中,Step2:采用修正的共軛梯度法求解。求解的具體實現步驟如下:

② 令k=0時,計算梯度

④ 第k+1次優化向量:

⑤ 修正:如果第k次優化向量向量中第j個位置處的數小于0,則將這個數的值設為0,同時令s(k),向量中第j個位置處的數置0,其余的數不變;

⑥ 第k+1次梯度

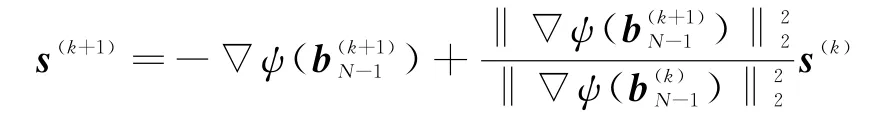
⑦取k=k+1。返回步驟③。修正:循環有限的次數L。上標k表示迭代次數。

Step3:再次確保優化碼b在約束的可行域內,從而得到波形優化碼a。由Step2求出b N-1,根據b N-1和b1之間的關系,求出b1。如果b1＜01時,令b1=01。對優化變量b進行以下處理:b=e b/‖b‖1,其中‖·‖1是向量的1范數,使得變量b滿足約束條件。

由于本文采用的共軛梯度法可以解決無約束的優化問題,通過函數的梯度來構造共軛方向,僅利用一階導數信息,具有運算量小、穩定性高、收斂速度快的優點。同時針對式(13)的優化問題,本文對算法進行了部分修正:為了使得優化速度快,實時性好,采用有限的循環次數進行碼的優化求解;為了保證優化變量在可行性的范圍內,需要對求解得到變量進行判斷。修正部分的算法運算量也極小。

4 計算機仿真和分析

仿真中假設協方差矩陣C和M以及動目標的多普勒頻率的范圍可通過一些預處理的方式獲得。接收端接收到的是高斯白噪聲,其協方差矩陣為M,噪聲的方差接收到的雜波,其特點是雜波譜為高斯型,雜波協方差矩陣中的各個元素的值為

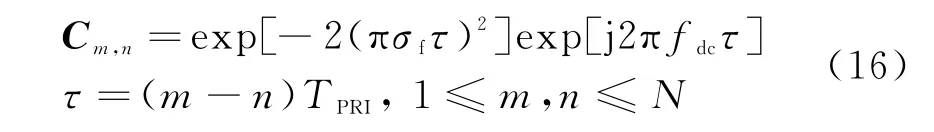
式中,σf=0.1為雜波譜寬的標準偏差,fdc=10 Hz為雜波的多普勒頻移,發射脈沖的重復周期TPRI=100μs。動目標多普勒角頻率范圍v=[-2 000,2 000](rad/s)。算法迭代循環次數設為L=200。

為了驗證本文算法的有效性,定義改善因子為

CPI中碼長N分別為8,16和32。采用本文SGMCODE算法得到優化碼與未經優化的碼(發射碼)進行比較,計算在不同的發射能量(即e不同)和動目標多普勒頻率在以上給定范圍內為均勻分布情況下的SCNR的變化,如圖1所示。由圖可以看出,對發射信號進行優化編碼提高了回波信號的SCNR,從而改善了對動目標檢測性能。

應用文獻[7]中重新設置參數的凸優化算法(Convexification via Reparametrization,Co Re)、直接碼設計的循環算法(Cyclic Algorithm for Direct Code Design,CADCODE)和本文的SGMCODE算法,不同的碼能量和目標多普勒頻率在以上給定范圍內為均勻分布情況下,分別求解碼長N=16時的優化碼,并得到各自對應的SCNR的值,與未編碼情況下得到的SCNR作對比,如圖2所示。3種算法的SCNR值近似相同,都高于未編碼情況下回波信號的SCNR。圖3中進一步計算出3種算法的改善因子,數值非常接近,并且在各個碼能量限制條件下都大于2 d B,可見對發射信號進行優化編碼改善了對動目標的檢測性能,3種優化碼的性能近似相同。

圖1 SGMCODE算法與未編碼的SCNR

圖2 CoRe,CADCODE和SGMCODE算法與未編碼的SCNR

圖3 Co Re,CADCODE和SGMCODE算法分別求得改善因子

由于算法復雜度與計算實時性之間一直存在著矛盾,因此要考量這3種算法求解優化碼的平均運行時間。如表1所示,本文算法SGMCODE在求解優化碼運行時間最短。本文算法中的循環次數L=200時,優化碼的性能在圖2和圖3中已分析。為了進一步驗證本文的實時性能,圖4顯示了循環次數L與求解優化碼的運行時間的關系,當循環次數L=200,運行時間t=0.425 6 s,小于其他兩種算法。可見編碼設計過程中,本文算法運行時間最短,實時性能好,更有利于實現。

表1 3種算法的平均運行時間

圖4 SGMCODE算法中循環次數L與求解優化碼的運行時間的關系

綜上所述,在信號相關雜波和白噪聲情況下,采用本文SGMCODE算法,有以下優點:首先,采用脈間編碼得到的SCNR大于未編碼的SCNR,優化碼改善了動目標的檢測性能;其次,不同的碼能量和動目標多普勒頻率在以上給定范圍內為均勻分布情況下,用本文SGMCODE算法所求得的最優碼與CoRe和CADCODE算法的最優碼求得SCNR近似,但在3種算法中,SGMCODE算法運行時間最短,實時性能好。

5 結束語

本文針對當前認知雷達的基本結構作了簡介;研究了基于慢時間域脈沖編碼的MTD雷達信號新模型,討論了SCNR改善的可行性;提出了用于SCNR改善的脈沖編碼優化設計準則,給出了優化問題的簡化方法,并針對CCQP問題提出了一種基于簡約梯度的編碼設計方法。此外,與Co Re和CADCODE算法作對比,結果表明,在高斯白噪聲和與信號相關的雜波環境下,針對未知多普勒頻率的動目標檢測問題,采用本文的方法對脈間編碼進行優化,使得問題復雜度變小,運算量小,處理速度快,實時性能顯著提高,更有利于對動目標實時檢測。

[1]HAYKIN S.Cognitive Radar:A Way of the Future[J].IEEE Signal Processing Magazine,2006,23(1):30-40.

[2]石榮,鄧科,閻劍.雷達認知能力提升及其與EW的智能博弈[J].雷達科學與技術,2015,13(3):228-232.SHI Rong,DENG Ke,YAN Jian.Cognition Improvement for Radar and Its Intelligent Game with EW[J].Radar Science and Technology,2015,13(3):228-232.(in Chinese)

[3]PILLAI S U,YOULA D C,OH H S,et al.Optimum Transmit-Receiver Design in the Presence of Signal-Dependent Interference and Channel Noise[C]∥Thirty-Third Asilomar Conference on Signals,Systems and Computers,Pacific Grove,CA:IEEE 1999:870-875.

[4]GUERCI J R,PILLAI S U.Theory and Application of Optimum Transmit-Receive Radar[C]∥IEEE Internal Radar Conference,Alexandria,AV:IEEE,2000:705-710.

[5]AUBRY A,DE MAIO A,PIEZZO M,et al.Cognitive Radar Waveform Design for Spectral Coexistence in Signal-Dependent Interference[C]∥IEEE Radar Conference,Cincinnati,OH:IEEE,2014:474-478.

[6]AUBRY A,DE MAIO A,PIEZZO M,et al.Radar Waveform Design in a Spectrally Crowed Environment via Non-Convex Quadratic Optimization[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(2):1138-1152.

[7]NAGHSH M M,SOLTANALIAN M,STOICA P,et al.Radar Code Design for Detection of Moving Targets[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(4):2762-2778.

[8]KAY S M.Fundamentals of Statistical Signal Processing,Volume II:Detection Theory[M].Upper Saddle River,NJ:Prentice-Hall,1998:248-332.

[9]NAGHSH M M,SOLTANALIAN M,STOICA P,et al.A Doppler Robust Design of Transmit Sequence and Receive Filter in the Presence of Signal-Dependent Interference[J].IEEE Trans on Signal Processing Magazine,2014,62(4):772-785.

[10]黃平,孟永鋼.最優化理論與方法[M].北京:清華大學出版社,2009:91-92.