基于虛擬陣列變換的共形陣列信號DOA估計
(中國人民解放軍92785部隊,河北秦皇島066200)
0 引言
共形陣列是一種與載體表面共形的天線陣列,由于其具有安裝簡化、波束掃描范圍廣、RCS小等優點[1-3],在現代飛機、導彈、衛星等設備均有重要的應用。共形陣列信號的二維角度估計問題是共形陣列信號處理中的重要內容,其在民用和軍事上都有重要意義,已受到廣泛關注。目前,國內外學者在共形陣列信號波達方向估計(Direction of Arrival,DOA)方面已經做了大量研究工作[3-10]。比如文獻[3]以圓柱共形陣列為例,采用多維MUSIC譜估計方法實現了DOA估計,但其需要二維譜峰搜索,運算量大,不適用于工程實際;文獻[4-7]通過合理劃分陣列使其滿足旋轉不變結構,從而實現柱面陣列和錐面共形陣列的DOA估計。但其方法對陣列形狀要求高,并不能適用于其他共形陣列。可以說,關于共形陣列信號DOA估計問題還有許多值得進一步研究的工作。本文給出了一種利用虛擬陣列變換的思想,采用ESPRIT算法和MUSIC算法相結合的方法實現了共形陣列信號二維角度估計。算法對陣列形狀限制小,估計性能良好。以圓柱共形陣列為例,對算法性能作了仿真驗證。
1 虛擬陣列變換方法
虛擬陣列變換方法[8]是將空間區域進行劃分,針對某個感興趣區域,在保證盡量小的變換誤差下,將原始陣列接收數據變換為虛擬陣列接收數據。其主要是利用兩個陣列導向矢量的變換關系獲得陣列數據變換關系。由于經虛擬變換得到虛擬陣列是預先期望的,因此,可以使用一些經典的參數估計方法。從虛擬變陣列變換的原理上看,虛擬陣列變換方法適用于任意陣列。下面介紹一下虛擬陣列變換的實現過程。
對布置于三維空間中幾何結構任意的陣列,如圖1所示,假設感興趣的區域為Θ=[θ1,θr],且信號位于此區域。

圖1 布置于三維空間的任意陣列
將區域以間隔Δθ作均勻分割,即Θ=[θ1θ1+Δθθ1+2Δθ…θr-Δθθr],那么原始陣列的陣列流型矢量矩陣為

假設希望經過虛擬變換得到虛擬陣列的流型矢量矩陣為ˉA,則在同樣的空間區間內,有

那么,原始陣列和虛擬陣列之間可以通過虛擬變換關系實現近似變換,即滿足

同理,原始陣列和虛擬陣列的導向矢量之間存在如下關系:

顯然,由原始陣列到虛擬陣列的變換過程中,會存在變換誤差。因此,求取變換矩陣B,可以看作如下計算:

式中,‖·‖F為Frobenius模。
由式(3)~(5)可以求得虛擬陣列變換矩陣:

那么,變換誤差可以定義為

顯然,理想情況下,變換誤差為零,此時虛擬變換過程是一個完全等價過程。但實際中,限于區域劃分、區域劃分間隔和虛擬變換陣列結構等限制,不可避免地存在誤差。因此,在實際計算中,一般會設置一個誤差允許范圍。
下面看一下,通過虛擬陣列變換,數據協方差矩陣是否有變化。假設原始陣列的接收數據協方差矩陣為背景噪聲為高斯白噪聲,其功率為σ2I,則有

虛擬陣列的協方差矩陣可表示為

顯然,從式(8)可以看出BHB≠I,即原始陣列白噪聲被污染為色噪聲。因此,要想利用虛擬陣列的協方差矩陣ˉR,必須預白化色噪聲。那么可以將變換矩陣B修改為

那么,有THT=I成立。此時,式(3)和式(4)所表示的原始陣列和虛擬陣列的變換關系變為

此時,虛擬陣列的數據協方差矩陣可寫為
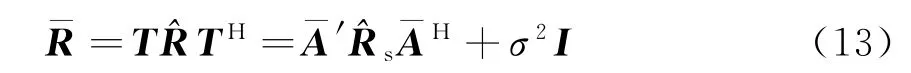
那么,利用式(13)得到的虛擬陣列協方差數據即可采用參數估計方法。需要注意的是,此時所對應的流性矢量矩陣ˉA′是經虛擬變換后的虛擬陣列的流行矢量矩陣。至此,對虛擬陣列變換方法作了簡單的介紹。下面將介紹具體的參數估計方法。
2 基于虛擬陣列變換的角度估計方法
針對共形陣列,利用虛擬陣列變換思想,采用ESPRIT算法和MUSIC算法相結合的方法實現二維角度估計。
空間任意M元陣列如圖2所示,第m個陣元的位置為p m=(x m,y m,z m)。假設有K個已知頻率為f0的空間窄帶信號源s1(t),s2(t),…,s K(t)入射到陣列,其入射角分別為{(θ1,?1),(θ2,?2),…,(θk,?k),…,(θK,?K)}。假設各陣元輻射方向圖均為g(θ,?)。當陣列存在較大曲率時,各陣元會受曲率影響,造成各陣元接收的信號強度不同。因此,這里將第m個陣元的真實接收方向圖記為g′m(θ,?)。

圖2 空間任意M元陣列
首先確定希望虛擬變換后的虛擬陣列結構。考慮到實際共形陣列的幾何結構可能多樣,因此采用一種普適的方法。假設虛擬陣列的幾何結構與原始陣列相同,只是沿著Z軸方向作了平移d z,令d z=λ/4。設虛擬變換的觀察區域俯仰向為Θ=[θ1,θr],方位向為Φ=[φ1,φr],其中{θk∈Θ,?k∈Φ}。那么,原始陣列流型矢量矩陣A(θ,φ)和虛擬陣列流型矢量矩陣ˉA(θ,φ)有如下關系:
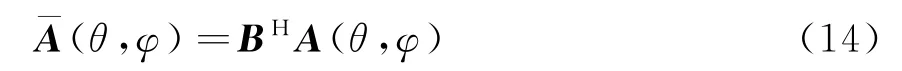
則虛擬陣列變換矩陣為

在獲得虛擬變換陣列后,可以近似獲得虛擬陣列接收數據。這樣,相當于擁有了原始陣列和虛擬陣列兩組接收數據。由于虛擬陣列與原始陣列存在固定的位置關系,可以采用ESPRIT算法[7]進行參數估計。這里僅是以沿Z軸方向作了平移,實際上只要保證虛擬陣列與原始陣列幾何結構相同,同樣可以將原始陣列沿著X軸或者Y軸方向作平移。
由于陣元方向圖對算法無影響,這里將陣元輻射方向圖認為是全向,則原始陣列和虛擬陣列的接收數據可以寫成:

式中:S(t)=[s1(t),s2(t),…,s K(t)]T;N(t)為陣列接收噪聲矩陣;

如果將兩個陣列的數據模型合并,可得


由旋轉不變子空間原理,可知
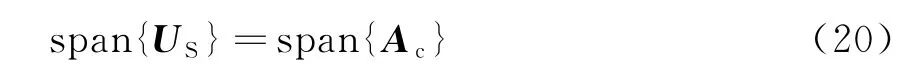


由于原始陣列和虛擬陣列幾何結構完全相同,由其旋轉不變性,可以利用最小二乘的方法求出旋轉不變矩陣Ψ:

對Ψ進行特征值分解,得到的K個特征值即對應著Ψz中對角元素,這樣就可以求出K個入射信號的俯仰角。如果將原始陣列分別沿著X軸或者Y軸平移,作類似處理,就可以求出空間入射角的俯仰角和方位角。這里只利用沿著Z軸平移,求出空間入射信號的俯仰角度。設為對Ψ特征分解得到的第k個特征值,則信號的俯仰角可以通過下式求得:

為了提高參數估計精度,這里采用文獻[8]的方法,在獲得信號俯仰角估計后,利用MUSIC算法作方位向的估計。由于采用虛擬陣列變換的方法,因此方位角搜索范圍為Φ=[φ1,φr]。這是在小區間內的一維譜峰搜索,相比于全空間二維譜峰搜索,其運算量較小。
M USIC算法的譜估計公式為

至此,可以通過式(24)和式(25)對空間二維入射角進行估計。
下面給出算法主要步驟:
5)計算旋轉不變矩陣Ψ,對Ψ進行特征分解;
6)由式(24)估計信號源俯仰角度;
7)根據估計出的俯仰角度和虛擬變換觀察區域Φ=[φ1,φr]確定參數范圍,對式(25)進行譜峰搜索,找到極大值即對應信號源入射方向。
3 仿真實驗
圓柱共形陣列其幾何結構是中心對稱旋轉體,根據文獻[1]提出的子陣分割思想,將圓柱共形陣列進行分割,這樣只需研究子陣性能即可。仿真采用如圖3所示的3×3圓柱陣共形陣列,圓柱半徑R=λ,信號波長λ=c/f0。共分3層,兩層陣元間距d z=λ/4。每層陣元等角度分布,其相鄰陣元夾角α=15°。陣元采用非極化全向陣元,即g(θ,?)=|J2(πεsinθ)-J0(πεsinθ)|。根據陣列結構將觀察區域作如下劃分,俯仰向為80°~100°,間隔0.1°;方位向為5°~25°,間隔0.1°。虛擬陣列設置為原陣列沿Z軸正向平移λ/4。
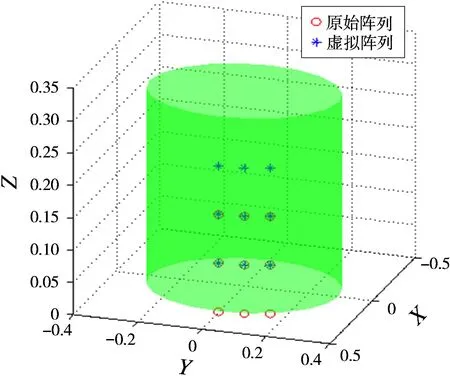
圖3 圓柱共形陣列
設有2個頻率為f0的空間窄帶信號源入射到陣列,信噪比(SNR)均為20 dB,其二維角度參數(θ,φ)(其中,θ代表俯仰角,φ代表方位角)為(85°,15°)和(95°,20°),采樣快拍數為500,偽快拍數為50,做50次蒙特卡羅仿真實驗。圖4是角度估計結果。
從圖中可以看出,算法可以估計出信源的二維入射角度。同時看到估計存有偏差。定義信源k的角度估計均方根誤差(RMSE)為
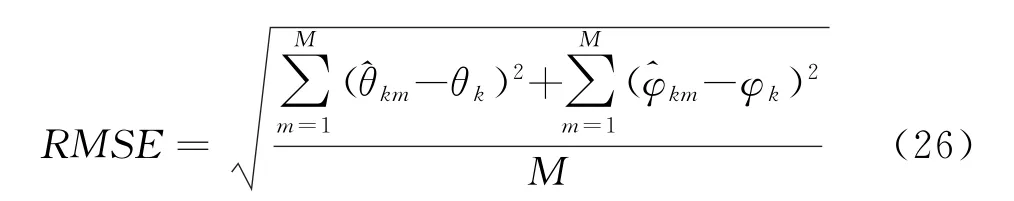

圖4 角度估計結果
圖5是角度估計誤差隨信噪比的變化曲線,可以看出,隨著信噪比的增加,估計性能逐漸提高。在信噪比為25 dB開始趨于穩定。在仿真時發現,算法在低信噪比時性能較差,所以信噪比選擇從10 dB開始。其誤差主要受到虛擬變換誤差和算法誤差兩個方面的影響。因此,兩種算法均對信噪比存在約束。
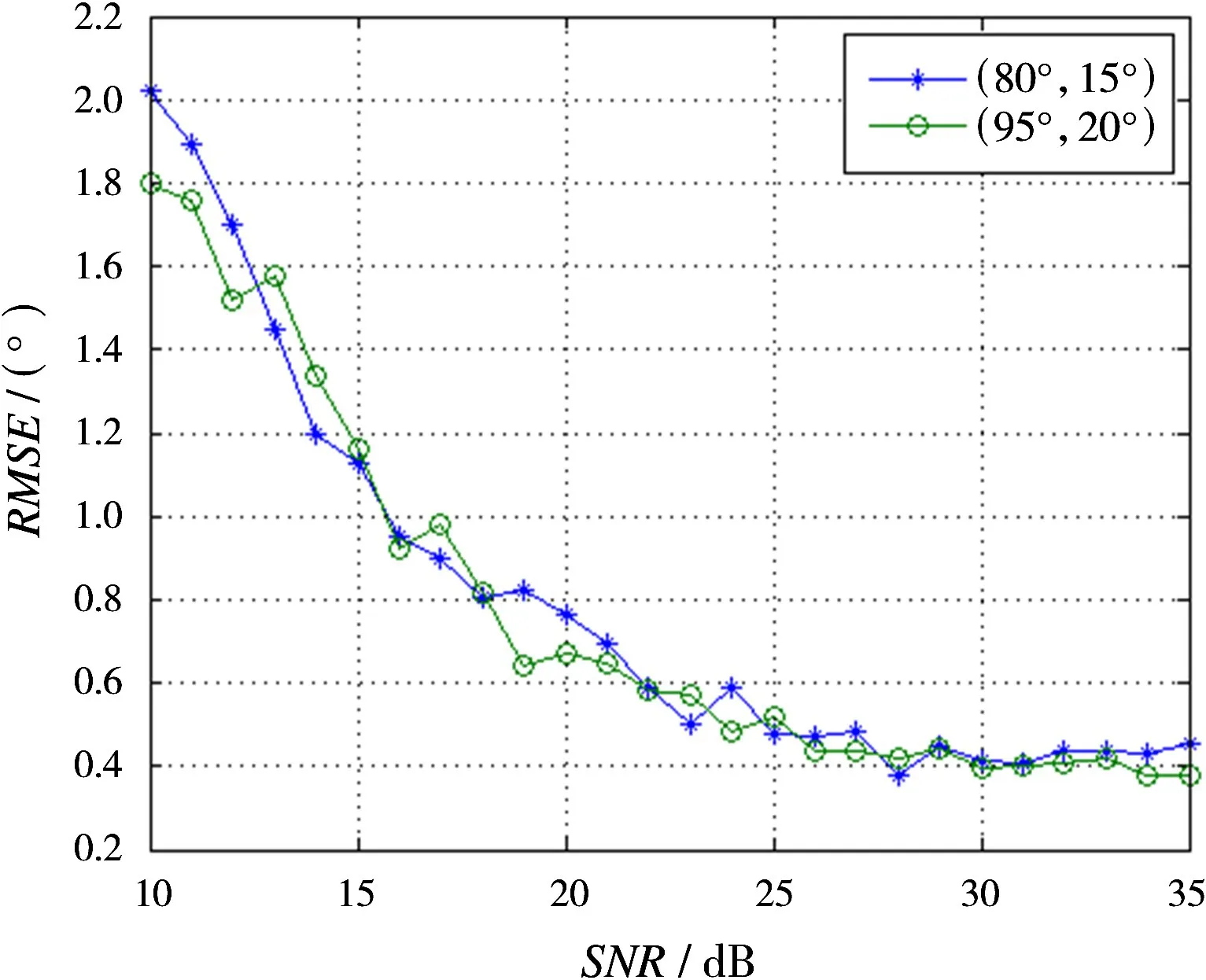
圖5 角度估計結果的RMSE隨信噪比變化曲線
圖6是角度估計誤差隨采樣快拍數的變化曲線。可以看出,當快拍數增加到900時,算法估計性能逐漸趨于穩定。

圖6 角度估計結果的RMSE隨采樣快拍數變化曲線
4 結束語
本文利用虛擬陣列變換思想,采用ESPRIT算法和MUSIC算法相結合的方法實現了共形陣列信號二維角度估計。以圓柱共形陣列,通過仿真實驗對算法有效性進行了驗證。算法對陣列形狀限制小,性能良好。關于共形陣列信號參數估計還有許多值得繼續深入研究的工作,比如共形陣列信號極化、頻率參數估計問題等。
[1]ZOU L,LASENBY J,HE Z.Direction and Polarisation Estimation Using Polarised Cylindrical Conformal Arrays[J].IET Signal Processing,2012,6(5):395-403.
[2]ZOU Lin,LASENBY J,HE Zishu.Pattern Analysis of Conformal Array Based on Geometric Algebra[J].IET Microwave,Antennas&Propagation,2011,5(10):1210-1218.
[3]齊子森,郭英,王布宏,等.共形陣列天線MUSIC算法性能分析[J].電子與信息學報,2008,30(11):2674-2677.
[4]郭英,高梅,張樹銀,等.基于旋轉不變子空間原理的共形陣列DOA與極化狀態聯合估計[J].上海交通大學學報,2013,47(7):1137-1142.
[5]YANG P,YANG F,NIE Z P.DOA Estimation with Sub-Array Divided Technique and Interpolated Esprit Algorithm on a Cylindrical Conformal Array Antenna[J].Progress In Electromagnetics Research,2010,103(1):201-216.
[6]張樹銀,郭英,齊子森.錐面共形陣列信源方位和極化參數的聯合估計算法[J].電子與信息學報,2011,33(10):2407-2412.
[7]SI W,WAN L,LIU L,et al.Fast Estimation of Frequency and 2-D DOAs for Cylindrical Conformal Array Antenna Using State-Space and Propagator Method[J].Progress In Electromagnetics Research,2013,137(1):51-71.
[8]王永良,陳輝,彭應寧,等.空間譜估計理論與算法[M].北京:清華大學出版社,2004.
[9]李杰然,許稼.共形陣列信號DOA和極化狀態聯合估計研究[J].雷達科學與技術,2015,13(2):159-163.LI Jieran,XU Jia.Joint Estimation of 2D-DOA and Polarization Based on Conformal Array[J].Radar Science and Technology,2015,13(2):159-163.(in Chinese)
[10]孫學軍,張高毅,唐斌,等.基于二次虛擬內插的圓陣接收2D-DOA分離估計[J].電子與信息學報,2008,30(8):1890-1892.

