基于FPGA的并行DDS結構設計?
(電子科技大學電子工程學院,四川成都611731)
0 引言
直接數字頻率合成器(DDS)是Tierney等[1]于1971年提出的一種全新的頻率合成技術,它相對傳統技術具有頻率分辨率高、頻率轉換時間快、易于合成復雜波形和相位連續等優點。隨著技術的不斷發展,它在雷達、通信、電子儀表儀器等領域具有廣泛的應用。然而,人們漸漸發現這種DDS結構最大的缺點就是不能得到很高的輸出頻率。由奈奎斯特采樣定律可知,輸出頻率應小于采樣頻率的一半,而在實際工程中輸出頻率只有其40%。FPGA作為一種可編程的數字集成電路,具有開發周期短、功能強、可靠性高和保密性好等優點,因此用FPGA實現DDS具有更明顯的優勢。本文利用FPGA實現四路并行DDS的結構,在相位累加器中結合了流水線結構,相幅轉換過程中將相位分為粗調和細調兩個部分,粗調仍用ROM實現,細調則利用角度旋轉的方法迭代。這樣,在提高輸出頻率、保證無雜散動態范圍的同時也擴大了頻譜寬度。
1 基本原理
DDS具體結構如圖1所示,包括相位累加器(PA)、相幅轉化器(SCMF)、數模轉換器(DAC)和低通濾波器(LPF)。N位相位累加器是由加法器和寄存器組成,頻率控制字K控制每次加法器步長,當其和大于2N時溢出,完成一個周期。相幅轉換器最初是利用查找表(ROM)來實現,即將一個周期的正弦或者余弦函數采樣2N個點存放在ROM中,并量化為W位的幅度值,然后用相位累加器作為地址控制輸出。系統時鐘為fclk,對應時間為1/fclk=Tclk,完成一個周期所需時間T0=Tclk×2N/K,所對應系統輸出頻率f0=fclk×K/2N。可以看出當K=1時,得到最小輸出頻率即頻率分辨率fmin=fclk/2N,由此可見當N很大時可以得到非常高的頻率分辨率。考慮到實際硬件條件,一般采用相位截斷的方法,只取相位高M位作為ROM的地址,從而減小ROM的深度。所得到的數字信號通過DAC,其類似于零階保持電路,將數字信號轉化為模擬信號。最后通過低通濾波器濾掉雜散,得到想要的波形。
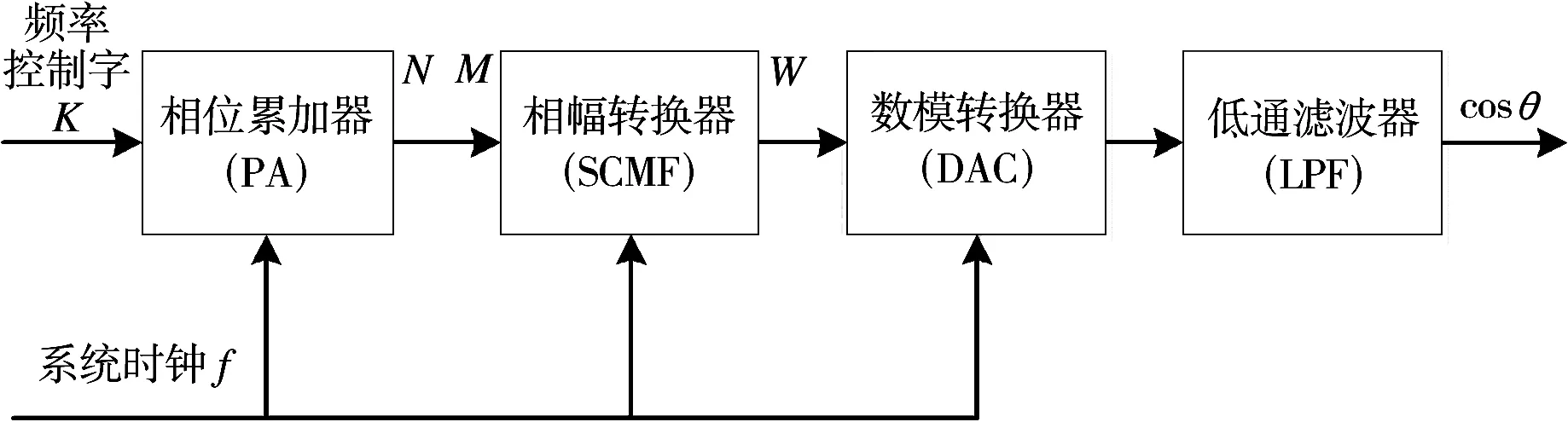
圖1 傳統DDS結構
2 相位累加器
運行高速系統就必須要用高速的相位累加器尋址。目前提高加法器運算速度的主要途徑[2]包括:1)加快進位的產生,提高進位傳遞速度,縮減進位傳播途徑;2)降低進位的產生,提高加法器運行速度;3)根據異步電路自定時的特點,將加法器運算速度從最壞延時提高到平均延遲。已有很多文獻根據這3種方法設計出高速加法器。如要用一個常規加法器實現N=32 bit的相位累加器,加法器要產生一次進位需要傳播的途徑太長。雖然節約了硬件,但是運行速度太慢。流水線結構是一種很常見的提高加法器速度的方法,它主要是利用縮減進位傳播途徑實現高速,其缺點是增加了硬件的消耗。例如將32位加法器可以分解為4個8位或者8個4位的加法器級聯。為了增加加法器的吞吐量,并行的相位累加器應運而生。圖2中采用4個加法器并行運算,能提高4倍的運算速度。
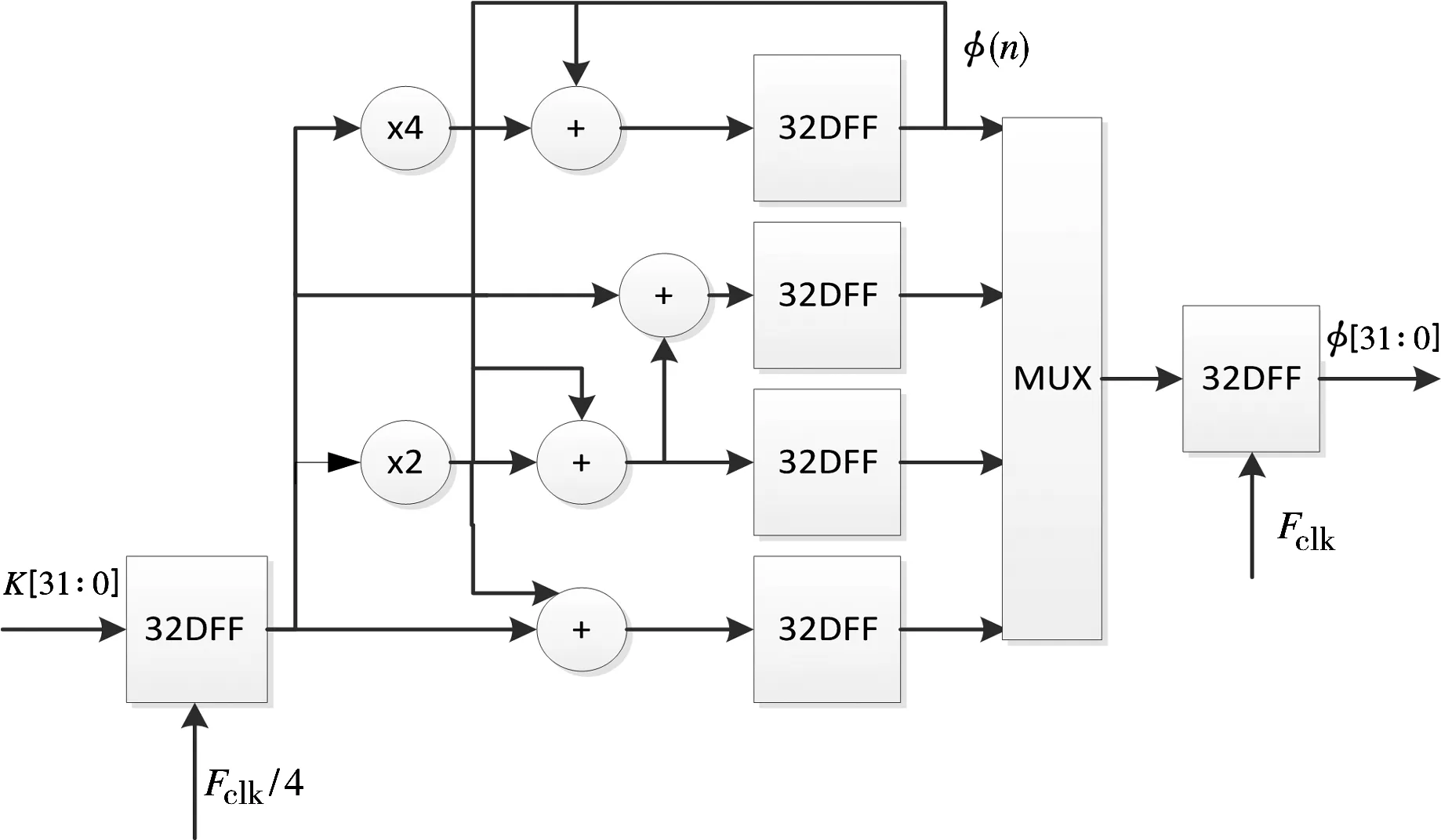
圖2 四路并行相位累加器
根據上圖結構,在4個時鐘周期后,得到如下四路輸出:
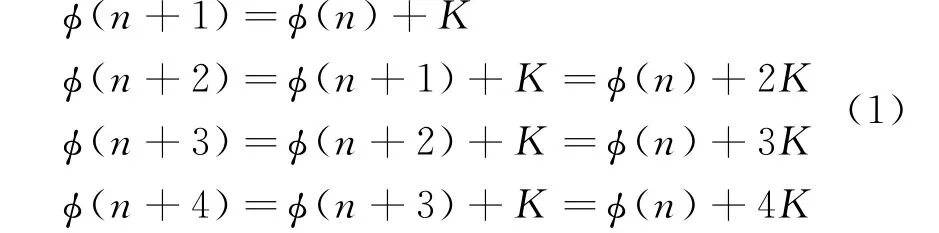
式中,?(n)為第n次相位累加器輸出,K為頻率控制字,這里假設32位。?(n+2)和?(n+4)可以在加?(n)之前,分別將K左移一位和左移兩位得到。?(n+3)就直接根據?(n+2)加上K得到。每一路時鐘為多路選擇器工作時鐘的四分之一。然而,這種結構相對于一個加法器增加了4倍的面積和功耗,其最大運行速度也僅僅為一個加法器的4倍。
為了得到更高的運行速度,可以將流水線和并行兩種結構相結合得到PPA(Pipelined Parallel Accumulator)結構[3]。即將32位加法器分解為兩個16位的上圖結構相級聯,這樣相對于單單的并行加法器每一路減小了一半的進位傳播途徑,從而進一步提高加法器速度。具體結構如圖3所示,頻率控制字K低16位在第一級計算得到四路相位的低16位,并將每一路產生的進位傳遞給對應的高16位。頻率控制字K高16位在第二級相對于第一級延遲一個周期后,四路同時運算得到四路相位的高16位。最后將高低位合并得到四路32位的相位,每一路相位值之間相差一個相位值K,從而為后面并行的DDS提供了相位偏移。

圖3 PPA結構
3 相幅轉換結構
傳統DDS結構中ROM對運行速度和芯片功耗有很大的影響,所以在輸出頻譜沒有較大影響的情況下應盡量減小ROM的容量。近幾十年人們提出很多方法,最常見的方法是利用正弦函數的對稱性,只將四分之一的波形幅度存在ROM中,然后犧牲地址高兩位來映射整個周期的波形。具體包括:
1)角度分解,將相位分解為粗相位和細相位。如將相位A分為高相位C和低相位F兩部分:
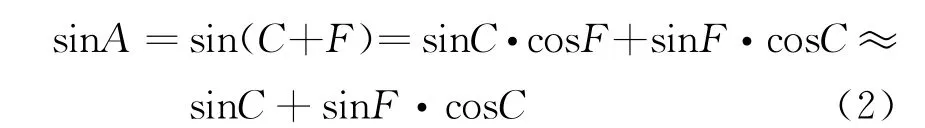
然后將兩項分別放入兩個RO M中,即用粗調和細調兩個小ROM來代替原來的一個大容量ROM。
2)角度轉換,最常見的方法就是應用CORDIC算法,如采用ROM與CORDIC相結合的方法[4]。
4)多項式近似,其中包括一階和高階近似,如泰勒公式展開。
本文相幅轉換將相位分為粗調和細調兩個部分,粗調部分仍然采用ROM的方式實現,細調部分應用類似于CORDIC算法的角度旋轉結構[5]。
3.1 角度旋轉算法
根據正交信號的性質可知,正弦函數在[0,π/4]的幅度值等于余弦函數在[π/4,π/2]的幅度值。因此,只需要存儲第一卦限θ=[0,π/4]的幅度值,即八分之一個周期。然后利用截斷后相位高三位將其映射到其他幾個卦限,得到一個周期波形,具體實現如表1所示。表中地址取反,是當MSB[3]為1時,ROM地址取其反碼。表中負數是根據映射規則在八分之一周期的幅度值前加上符號位。
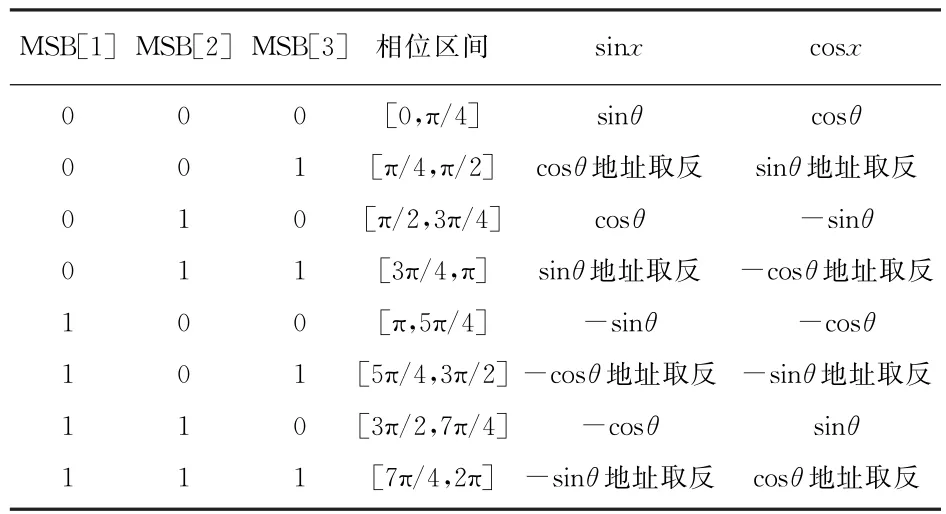
表1 卦限映射關系
在第一卦限中所有角度的弧度值是小于1的,也就都是大于零的小數。用二進制表示為θ=對b進行重新編碼:
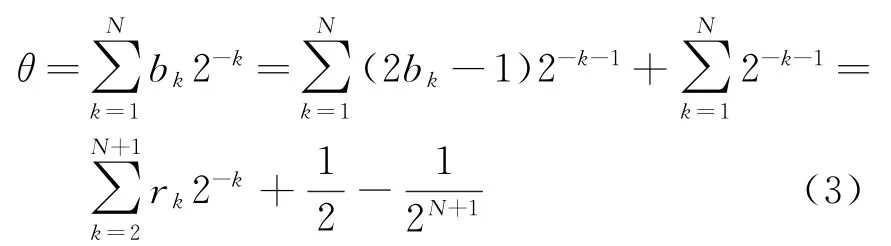
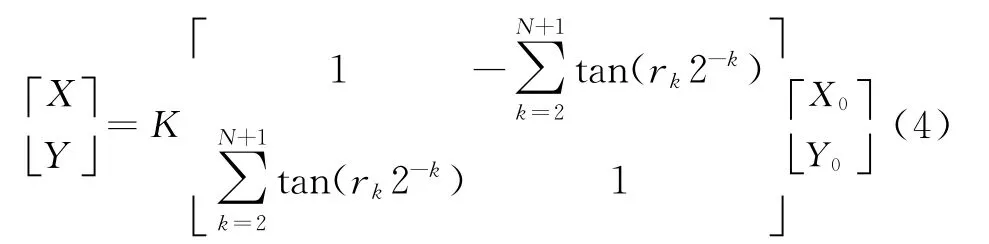
式中,X0=cosθ0,Y0=sinθ0,是一個常數。由于CORDIC算法中,第i次旋轉角度滿足αi=arctan2-i,通過判斷旋轉方向,移位相加得出結果。這里旋轉角度不同于CORDIC算法,因此不能簡單地通過移位相加實現。根據正切函數的泰勒公式展開式對于N位相位當k≥N/3時這里假設k=M+1滿足條件,也就是粗細相位分界位在M位,M+1位為低相位的MSB。此時,式(3)可以改寫為
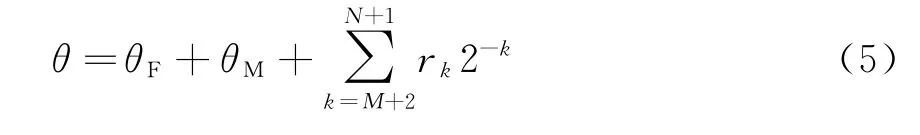
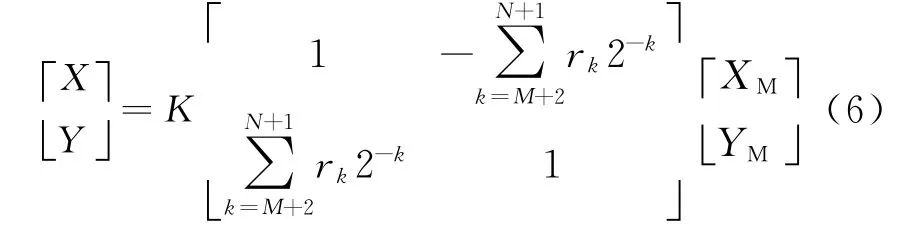
式中,XM=cos(θF+θM),YM=sin(θF+θM),同樣K為常數。此時,也可以同CORDIC算法一樣移位相加得到幅度。
3.2 細調部分二進制重新編碼
在式(6)中,求和項相當于一個有符號數的二進制數。可以把r k重新編碼成二進制補碼數:t k={0,1}
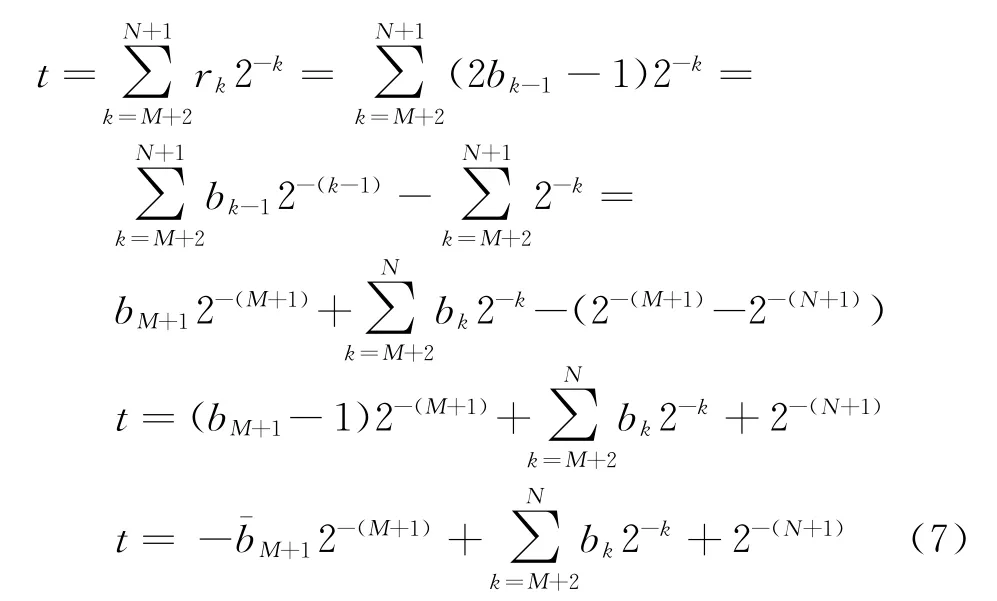
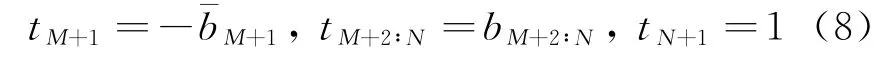
將低相位重新編碼后,變成有符號的數。因此在后面的運算中應作為有符號數處理,同時相位MSB[3]控制其是否取反碼。將K乘以XM,YM一起存進ROM中。式(6)可改寫為
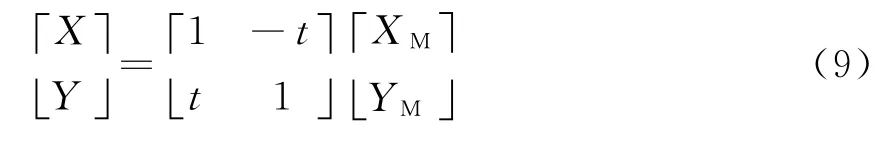
3.3 粗調部分
由于相位累加器輸出相位局限于[0,π/4]內,對于32位的相位控制字K而言,0和π/4分別相當于0和4294967295,所以粗細相位都應乘以π/4。為了避免浮點運算,這里相位沒有除以232。同時由式(6)知道K是獨立于t的常數,所以也可將直接乘以XM和YM存入ROM中。細相位乘以π/4在其他文獻中大都采用其泰勒展開式,通過移位相加得到。本文為了減小延遲和芯片功耗,根據關系式先用XM和YM乘以π/4分別得到XR和YR,并把數值存入另外兩個ROM中。由于相對于存放XM,YM的兩個ROM,XR和YR量化位數更少,其ROM容量更小。具體關系由式(10)給出:

圖4給出所采用的DDS結構。
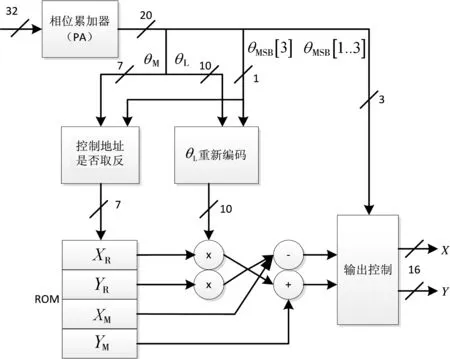
圖4 ROM+CORDIC算法的DDS結構
4 總體框架與仿真
本文采用四路并行的DDS結構,相位累加器采用圖3的PPA結構,每一路相幅轉換采用圖4結構。每一路頻率控制字相當于4K,相鄰兩路相位控制字差為K。以單路工作時鐘的4倍時鐘實現并串轉換,相當于四路數據相互內插。每一路輸出頻率為四路選擇器輸出為可見雖然頻率控制字和工作時鐘改變了,但是兩個輸出頻率是一樣的,輸出頻譜擴大了。具體結構如圖5所示。

圖5 四路并行DDS結構
選用Xilinx公司的XC6VLX240T芯片仿真,頻率控制字K為32位,相位截斷取高20位。存放XM和YM的ROM量化位數為17 bit,XR和YR量化位數為7 bit,輸出信號位數為16位。XST綜合后報告顯示,每一路最大工作時鐘可達236.351 MHz。這里系統輸入時鐘采用100 MHz,利用PLL倍頻設置每一路DDS工作時鐘200 MHz,系統總的工作時鐘為400 MHz,由于FPGA將數據傳給DAC,因此這里采用原語OSERDES1的ODDR模式。可知頻率分辨率約為0.186 Hz。由前面的分析可知,當工作時鐘為200 MHz時輸出頻率最大為80 MHz。圖6和圖7分別給出用Modelsim仿真頻率為200 MHz和25 MHz的I、Q信號。

圖6 頻率為200 MHz的I、Q仿真信號
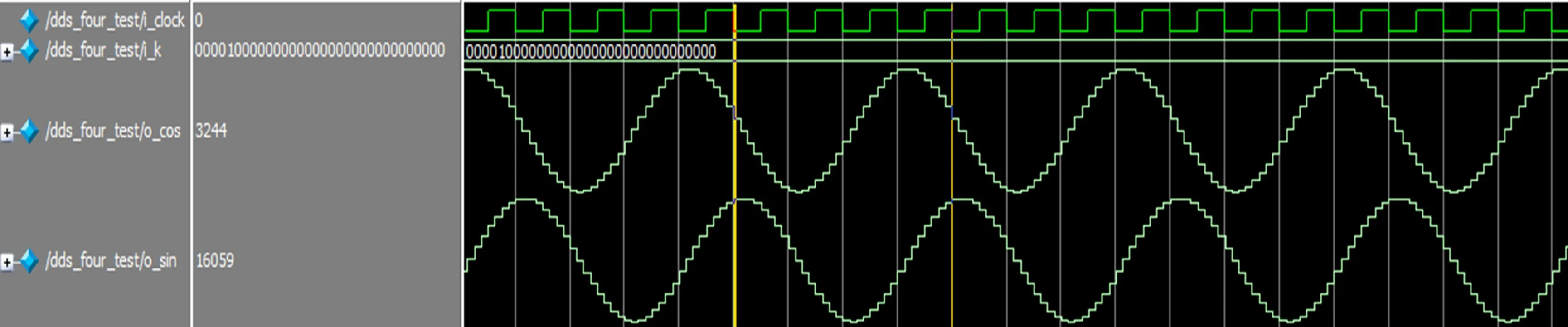
圖7 頻率為25 MHz的I、Q仿真信號
5 結束語
要滿足高速DDS結構,相位累加器要給出高速的尋址,同時ROM不能太大。流水線和并行加法器都能提高一定的運行速度,但是又各自存在著缺點。將兩種結構結合在一起,使得在速度和資源消耗方面做出了很好的平衡。減小ROM,雖然能提高一定速度和減小功耗,但是輸出波形質量不能得到保證。因此,結合類似CORDIC算法迭代能得到高精度波形的特性,在提高速度的同時兼顧了波形質量。然而,它又不同于傳統的CORDIC算法,每次都需要根據剩余角度判斷下一次的旋轉方向,從而影響運行速度。傳統結構中對于17位的相位尋址,需要ROM深度為217。而采用本文中的方法僅需27,大大減小了ROM容量,從而提高了速度和減小了功耗。20位的相位尋址使得具有約-120 dBc的無雜散動態范圍。當然在實際硬件實現的電路中還會存在相位噪聲等因素[6]影響波形性能。并行的DDS是通過提高采樣頻率,增大了輸出信號的頻譜,同時減小了總功耗,從而在雷達系統中具有廣泛的應用。
[1]TIERNEY J,RADER C M,GOLD B.A Digital Frequency Synthesizer[J].IEEE Trans on Audio and Electroacoustics,1971,19(1):48-57.
[2]袁浩,唐建,方毅.超前進位加法器的優化設計[J].通信技術,2014,47(3):339-342.
[3]YANG B D,CHOI J H,HAN S H,et al.An 800-MHz Low-Power Direct Digital Frequency Synthesizer with an On-Chip D/A Converter[J].IEEE Journal of Solid-State Circuits,2004,39(5):761-774.
[4]MADISETTI A,KWENTUS A Y,WILLSON A N.A 100-MHz,16-b,Direct Digital Frequency Synthesizer with a 100-dBc Spurious-Free Dynamic Range[J].IEEE Journal of Solid-State Circuits,1999,34(8):1034-1043.
[5]BERGERON M,WILLSON A N.A 1-GHz Direct Digital Frequency Synthesizer in an FPGA[C]∥IEEE International Symposium on Circuits andSystems,Melbourne,Australia:IEEE,2014:329-332.
[6]王勇.直接式頻率合成器相位噪聲限制因素[J].雷達科學與技術,2013,11(3):,329-334.WANG Yong.Phase Noise Limiting Factors of Direct Frequency Synthesizer[J].Radar Science and Technology,2013,11(3):329-334.(in Chinese)

