推導勻強電場中導體球的電荷面密度的簡單方法

推導勻強電場中導體球的電荷面
密度的簡單方法

鄭 金

(凌源市職教中心遼寧 朝陽122500)

摘 要：通過推導一個數學結論和電偶極子的場強公式，利用均勻帶電球體內部場強公式、等量異號電荷模型、鏡像電荷模型和偶極子模型以及等效法和疊加法，對勻強電場中導體球的電荷面密度的關系式給出兩種巧妙的推導方法.

關鍵詞：月牙形導體球等效法電荷面密度

收稿日期：(2014-11-14)

對于勻強電場中的導體球的電荷面密度關系式，在電動力學教材和一些物理文獻中，是利用拉普拉斯方程和勒讓德函數進行推導的，比較高深.下面利用一些等效物理模型和有關數學知識，對勻強電場中的導體球感應電荷面密度關系式給出兩種簡單的推導方法.

首先推導一個簡單的數學結論.如圖1(a)所示，兩個大小相等的圓不重合，相交于兩點M和N，設直線OA偏離中軸線的角度為θ，兩個圓心錯開的距離為d，月牙弦的長度為h=AB=OA-OB，其最大值為d，最小值為零. 弦長h隨直線OA的偏角θ而變化，θ越大，對應的弦長越小，那么弦長h與最大弦長d和偏角θ的數量關系是什么呢？

相交弦同側的優弧與劣弧圍成一個月牙形.兩圓心O1與O2連線的中點為O，過點O作徑向直線OA交優弧于點A，交劣弧于點B，把線段AB稱為月牙弦.

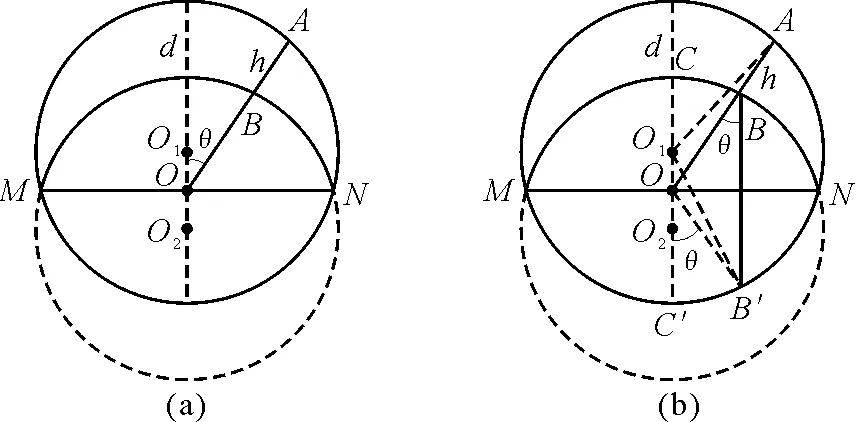
圖1

為了求弦長h，需分別求出OA和OB的長度，可通過構造兩個三角形利用余弦定理來求.如圖1(b)所示，連接O1A，得到一個三角形O1OA，其中半徑R=O1A所對的角度即直線OA與月牙形的中軸線的夾角為θ；兩圓的公共弦為MN，劣弧MCN與劣弧MC′N關于直線MN對稱，過點B作MN的垂線，與劣弧MC′N交于點B′，連接OB′，則OB=OB′，由對稱性可知OB′與OC′的夾角也為θ.連接O1B′，又得到一個三角形O1OB′，其中半徑R=O1B′所對的角度為180°-θ.

設OO1=l，則O1O2=d=2l.對三角形O1OA和O1OB′分別由余弦定理得

R2=l2+OA-OA·2lcosθ

R2=l2+OB′+OB′·2lcosθ

兩式聯立可得

OA-OB′=2lcosθ

由于

OB′=OB2l=d

所以月牙形的弦長為

h=AB=dcosθ

結論:兩個重合的圓錯開距離d而形成月牙形，若過兩圓心連線中點的直線與月牙形中軸線的夾角為θ，則月牙形截得直線的長度即月牙弦的長度為h=dcosθ，是余弦函數.

該數學結論對于空間月牙體同樣適用.下面利用這個結論推導勻強電場中導體球的電荷面密度.

【例1】如圖2(a)所示，在電場強度為E0的勻強電場中，放著一個半徑為R的金屬球.若球面上的一點A對應的半徑與場強正方向的夾角為θ，求金屬球表面的感應電荷面密度σ與角度θ的關系式.

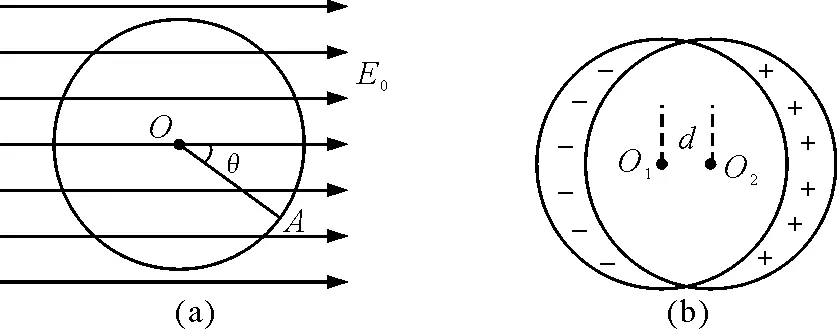
圖2

解法1:利用數學結論和均勻帶電球體模型

對于在勻強電場中的金屬球，左側表面出現負電荷，右側表面出現正電荷，球內合場強為零，即球面感應電荷在球內產生勻強電場，場強大小也為E0，但方向相反.因此可利用兩個大小相同的均勻帶有等量異號電荷的球體交疊來構建勻強電場中導體球的等效模型，即分別在兩個半徑為R的絕緣球內均勻分布等量異號電荷，左球帶負電，右球帶正電，設想將兩球互相交疊放入勻強電場中，球心不重合，而是沿電場方向稍微錯開距離d，如圖2(b)所示，兩球重疊部分正負電荷中和而形成電中性的空腔，即空腔內的電荷體密度為零；在邊緣形成兩個月牙體，其中電荷按原密度均勻分布.

當d→0時，空腔趨近于半徑為R的球體，月牙體幾乎趨近于兩個半球的表面.這與原題中的物理模型在空間幾何圖形上是等效的；雖然月牙體均勻帶電，但由于月牙體的厚度不均勻，因此離中軸線越近，電荷量越大，這與勻強電場中的導體球表面感應電荷的分布情況相一致，所以兩個物理模型在電荷分布趨勢及對稱性上是等效的.

可以證明，對于半徑為R，均勻帶電Q的球體內部距球心為r處的場強公式為

再推導兩個大小相同的均勻帶電的球體疊加區域的場強公式.如圖3(a)所示，設左、右兩球所帶的電荷量分別為-Q和+Q，可認為分別集中于球心O1和O2的點電荷，在重疊區域任取一點P，對兩個球心的矢徑分別為r1和r2，方向都指向點P，則負電荷在P點產生的場強矢量為

正電荷在P點產生的場強矢量為

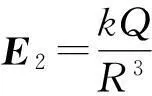
由矢量三角形可知點P處的合場強為

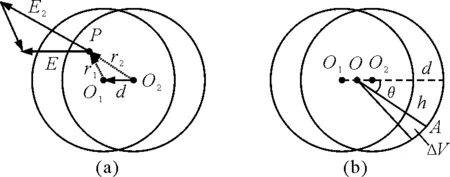
圖3

由于兩球心連線O2O1對應的矢量d1的大小恒定，方向恒定，則場強E恒定，表明在兩球體重疊區域的電場為勻強電場，即兩個月牙形帶電體在空腔內產生勻強電場，方向與外電場相反，使疊加區域內的合場強為零，這與勻強電場中的導體球內合場強為零的情況完全一致，因此兩個物理模型是等效的.

由

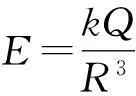
可知兩絕緣球所帶的電荷量大小為

則電荷體密度為

可用微元法求電荷密度，如圖3(b)所示，月牙體所截得中軸線的長度即月牙體的最大厚度為d，過兩球心連線O1O2的中點O作直線與月牙體的中軸線的夾角為θ，在其一邊附近作一立體角元dΩ，對應的微小錐體在月牙體內截取一段小柱體ΔV，設其底面積為ΔS，則其體積為ΔV=ΔS·h.只要求出厚度h與最大厚度d和偏角θ的數量關系，就可求出電荷密度.

由月牙形厚度公式可知，在圖3(b)中月牙體的厚度隨偏角變化的關系式為

h=dcosθ

則立體角元在月牙體內截得小柱體的體積為

ΔV=ΔS·dcosθ

因此小柱體所帶的電荷量為

ΔQ=ρΔV

所以該處的電荷面密度為

當兩球心很近時，即d→0時，重疊區域趨近于球體，則直線OA與月牙形的中軸線的夾角趨近于球的半徑與外場強正方向的夾角，所以金屬球表面的感應電荷面密度與角度θ的關系式

解法2:利用像電荷模型和電偶極子模型

如圖4(a)所示，一電偶極子的電偶極矩表示為p=ql，點P到偶極子中心O的距離為r，r與l的夾角為θ.在r?l時，可求出P點的電場強度E在OP方向的分量Er.

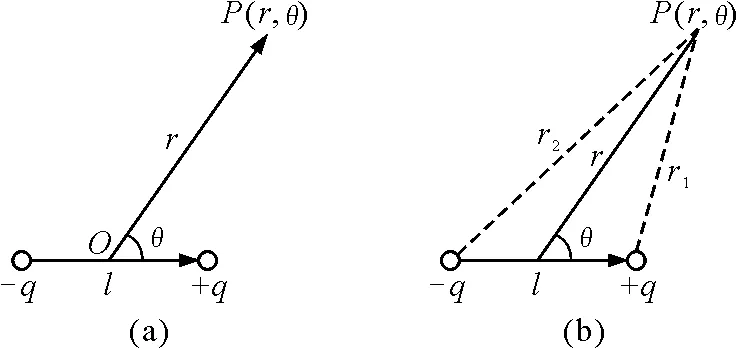
圖4

如圖4(b)所示，設兩個點電荷到P點的距離分別為r1和r2，可知P點的電勢為

由于r?l，則

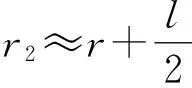
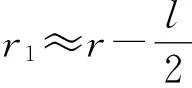
因此

r2-r1≈lcosθ

r2·r1≈r2

所以

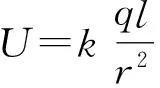
可知P點的電場強度E在OP方向的分量為

如圖5所示，兩個點電荷q和-q分別放在過球心O的直線上關于球心對稱的位置，到球心的距離為a，a很大，q也很大，則在球心附近區域產生的電場近似為勻強電場，由點電荷場強公式和電場疊加可知場強大小為

為了使該物理模型與例題中的物理模型等效，那么場強應為

E=EO

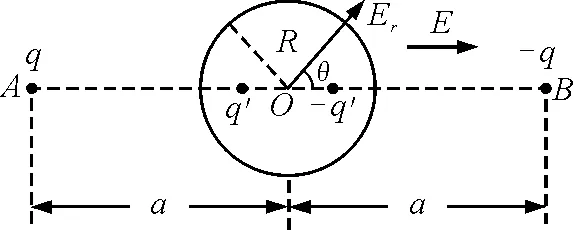
圖5

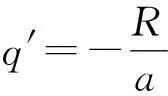
由一對等量異號點電荷±q組成的帶電體系，若它們之間的距離l比場點到它們中點的距離r小得多，則把這種帶電體系叫做電偶極子.偶極子在球面上任意點P產生的法向場強為

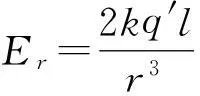
式中

r=R

則

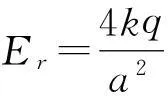
由于處于靜電平衡狀態導體表面的場強為4πkσ，則球面上P點的場強為

Er+EOcosθ=4πkσ

而

因此

2EOcosθ+EOcosθ=4πkσ

所以

角度θ是球面上的某點對應的半徑與勻強電場正方向的夾角，對于一定的角度θ，電荷面密度相同的各點分布在球面的同一圓周上.

參 考 文 獻

1沈晨.專題17——靜電場：原理與方法.中學物理教學參考，2005(11)：53，56

2趙凱華，陳熙謀.電磁學(上冊).北京：高等教育出版社，1988.43

3王浩川，等.構建一般化電荷模型求解靜電物理問題.物理通報，2014(6)：72