均值不等式在高中物理解題中的應用
均值不等式在高中物理解題中的應用*
楊紹林
(云南師范大學物理與電子信息學院云南 昆明650500;
昆明一中度假區分校金岸中學云南 昆明650031)
彭朝陽
(云南師范大學物理與電子信息學院云南 昆明650500)
中學物理實驗教學研究教學案例建設,編號:YJG2014-A05
摘 要:運用數學工具解決物理問題,是高考考查學生能力的方式之一,而高中物理問題中常出現求極值問題,如:最長、最大、最短、至少、最多等.這些問題滲透在物理中的運動學、力學、電磁學和電學等問題中.均值不等式是求解極值問題有效的方法,分為定和求積與定積求和兩種形式.在物理解題中有許多極值題可以構造出定和或定積的形式,進而求出最大值或最小值.
關鍵詞:極值問題均值不等式定和求積定積求和
作者簡介:楊紹林(1985-),男,在讀碩士研究生.
通訊作者:彭朝陽(1971-),男,教授,主要從事物理教育教學研究.
收稿日期:(2015-05-26)
每年各種各樣的高考模擬題、高考仿真卷、高考試題中,出現用均值不等式解題的極值問題較多,所以教師在平時的教學中應該多滲透用均值不等式來求解,不僅省時省力,學生用數學工具解決物理問題的能力也會得到提高.
但現在教師們多數停留在普通的數學求解和單純的解題,沒有把物理思想和解題規律進行融合和歸納總結,使得學生不得解極值問題的精髓.就這些問題,下面例舉一些均值不等式的應用,以期加深對此類問題的理解.
1均值不等式在高考模擬題中的應用
【例1】如圖1半徑為R的半圓形光滑凹槽固定,質量為m的小球Q,從最高點A運動至B的過程中,在什么位置重力做功的功率最大?最大值是多少?

圖1
解析:設小球Q運動到A與B間某位置P時,半徑OP與水平方向成θ角,此時瞬時速度為v,則此時重力的瞬時功率為
P=mgvcosθ
(1)
由機械能守恒定律的

(2)
將式(2)代入式(1)得
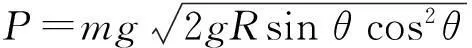
(3)
此時問題轉化為求極值
y=sinθcos2θ
(4)
將式(4)做數學變形如下

(5)
由均值不等式得
(6)


(7)

將式(7)代入式(3)得
(8)
【例2】如圖2所示,R1=2 Ω,R2=3 Ω,滑動變阻器的最大阻值R3=5 Ω,則在滑片從a端滑到b端的過程中,電流示數的最小值為多少?

圖2
解析:設滑片上部分電阻為Rx,則下部分電阻為(5-Rx) .
電路的總電阻為
利用均值不等式
(2+Rx)(8-Rx)≤
當(2+Rx)=(8-Rx)時,即Rx=3 Ω時,R最大,電流表的示數最小.此時
電流表示數
本題的極值問題也是屬于均值不等式的“定和求積問題”,即(2+Rx)和(8-Rx)的和是定值,那么(2+Rx)(8-Rx)必有最大值[1].
【例3】如圖3所示,已知電源電動勢為E,內阻為r,開關S閉合后,求R為多大時,電源輸出功率有最大值 ?
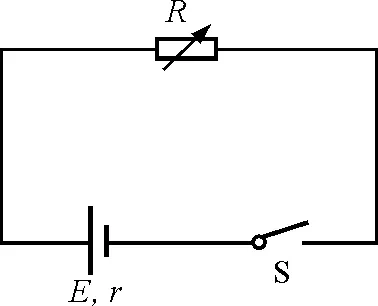
圖3
解析:由題意可知,電源的輸出功率最大值為
由均值不等式可知
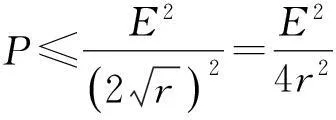
2均值不等式在高考仿真卷中的應用
【例4】如圖4所示,AOC是光滑的直角金屬導軌,AO沿豎直方向,OC沿水平方向,ab是一根金屬直棒,如圖立在導軌上,b端比a端更靠近O點.它從靜止開始在重力作用下運動,運動過程中b端始終在OC上,a端始終在AO上,直到ab完全落在OC上.整個裝置放在一勻強磁場中,磁場方向垂直紙面向里,則ab棒在運動過程中
A.感應電流方向始終是b→a
B.感應電流方向先是b→a,后變為a→b
C.棒受磁場力方向與ab垂直,如圖中箭頭所示方向
D.棒受磁場力方向與ab垂直,開始如圖中箭頭所示方向,后來變為與箭頭所示方向相反
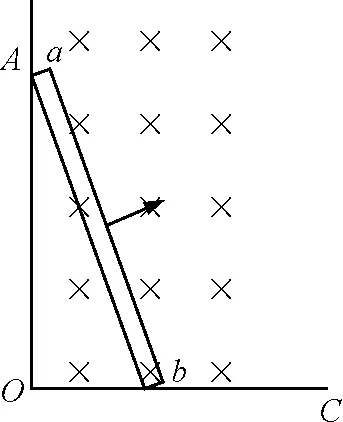
圖4
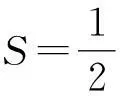
本題屬于均值不等式的“定和求積問題”,但根據均值不等式原理可知,這題兩個變量相等時,它們的乘積有最大值[2].
【例5】水平傳送帶以2 m/s的速度做勻速直線運動,傳送帶的兩端距離為2 m,將一物體輕輕放在傳送帶的一段,物體由一端運動到另一端經歷的時間為11 s,則物體與傳送帶之間的動摩擦因數是多少?(g=10 m/s)要求物體從傳送帶一端A運動到另一端B用時最短?

t1+t2=11
v=μgt1
聯立以上各式得
μ=0.1
由于物體先勻加速再勻速運動,則運動的總時間
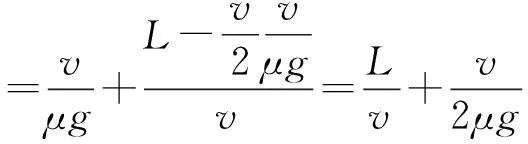
由均值不等式可知


3均值不等式在高考真題中的應用
【例6】(2010年高考江蘇卷第14題)在游樂節目中,選手需借助懸掛在高處的繩飛越到水面的浮臺上,小明和小陽觀看后對此進行了討論如圖5所示,他們將選手簡化為質量m=60 kg的質點,選手抓住繩由靜止開始擺動,此時繩與豎直方向夾角α=53°,繩的懸掛點O距水面的高度為H=3 m,不考慮空氣阻力和繩的質量,浮臺露出水面的高度不計,水足夠深,取重力加速度g=10 m/s2,sin53°=0.8,cos53°=0.6.若選手擺到最低點時松手,小明認為繩越長,在浮臺上的落點距岸邊越遠;小陽卻認為繩越短.落點距岸邊越遠請通過推算說明你的觀點.

圖5
分析:由圓周運動知識可知最低點松手時的速度,再由平拋運動可知水平位移的表達式,進而找到繩長與落點的關系.
解析:設選手從最低點開始做平拋運動速度為v,設浮臺上的落點距岸邊水平距離為x,平拋時間為t,則

x=vt
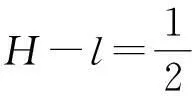
由以上各式解得
利用均值不等式

本題中的極值問題是屬于均值不等式中的“定和求積問題”,即l和H-l的和是定值,那么l(H-l)必有最大值.
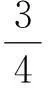
(1)求繩斷時球的速度大小v1,和球落地時的速度大小v2;
(2)問繩能承受的最大拉力多大;
(3)改變繩長,使球重復上述運動.若繩仍在球運動到最低點時斷掉,要使球拋出的水平距離最大,繩長應為多少?最大水平距離為多少?

圖6
解析:根據機械能守恒和動能定律可知,第(1)、(2)問中的解為
(3)設繩長為l,繩斷時球的速度大小為v3,繩承受的最大拉力不變,有
得
繩斷后球做平拋運動,豎直位移為d-l,水平位移為x,時間為t1.有
x=v3t1
由上式得
又由均值不等式得
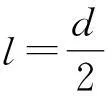
本題中的極值問題是屬于均值不等式中的“定和求積問題”,即l和d-l的和是定值,那么l(d-l)必有最大值[4].
綜上所述,均值不等式是處理物理問題的重要工具,在平時的物理教學過程中,教師不僅應善于利用均值不等式來分析和處理物理問題,還要引導學生總結使用它的方法和技巧,豐富高中學生的知識逐步培養學生利用均值不等式來處理物理問題的習慣和能力.
參 考 文 獻
1李海平、張瀚澤.高考模擬試題匯編.拉薩:西藏人民出版社,2013.10~17
2謝兆剛.全國各省市高考試題匯編.合肥:安徽教育出版社,2014.40~47
3魏萬青.金版教程.蘭州:甘肅教育出版社,2016.59
4曲一線.5年高考真題詳解.北京:首都師范大學出版社,2010.6~10

