基于空間時頻分布的高頻雷達(dá)接收陣校正?

(哈爾濱工業(yè)大學(xué)(威海)信息與電氣工程學(xué)院,山東威海264209)

0 引言

高頻地波雷達(dá)利用超分辨的信號處理算法實現(xiàn)信號的到達(dá)角(Direction of Arrival,DOA)估計[1-2],而這類算法的性能極大地受制于陣列誤差,當(dāng)誤差嚴(yán)重時甚至導(dǎo)致該類算法失效[3]。陣列校正可以分為有源校正和無源校正兩類。有源校正需要在天線陣遠(yuǎn)場放置一個以上的已知方向信源,而對于高頻地波雷達(dá)而言,遠(yuǎn)場位置在海面上,信源架設(shè)困難[4],而且天線陣誤差隨著外界散射場的變化而變化[5],因此有源校正不太適合高頻地波雷達(dá);無源校正是利用正常目標(biāo)的回波信號,通過陣列信號處理的方式,對目標(biāo)的方位與陣列的誤差進(jìn)行聯(lián)合估計,從而達(dá)到實時校正的目的。目前高頻地波雷達(dá)多采用無源校正方式進(jìn)行接收陣校正[6]。

無源校正的研究開始于20世紀(jì)80年代,主要的校正算法分為兩大類。第一類以1985年P(guān)aulraj與Kallath提出的利用無誤差情況下空間相關(guān)矩陣的Toeplitz結(jié)構(gòu)的方法[7]為代表,該類方法主要利用空間相關(guān)矩陣規(guī)律性的結(jié)構(gòu);第二類以1989年Weiss與Friedlander提出的通過構(gòu)造代價函數(shù)的方法[8-9]為代表,該類方法將誤差校正轉(zhuǎn)變?yōu)閰?shù)優(yōu)化問題。第一類算法要求較為準(zhǔn)確地估計出校正目標(biāo)的空間相關(guān)矩陣。時域信號由于未經(jīng)過多普勒分離,信號中包含整個頻段的信息,因此信噪比較低,很難滿足校正要求,而且實際應(yīng)用中也很難找到包含單個目標(biāo)的距離門。同時,高頻地波雷達(dá)需要較長的相干積累周期以獲得較高的信噪比,通常一個積累周期需要2～3 min,這會導(dǎo)致同一目標(biāo)可用的頻域快拍數(shù)很少[10]。文獻(xiàn)[11]證明了空間時頻分布(Spatial Time-Frequency Distribution,STFD)矩陣與空間相關(guān)矩陣具有相似的結(jié)構(gòu),并可以利用其進(jìn)行目標(biāo)的DOA估計。

本文針對上述陣列校正中空間相關(guān)矩陣估計困難的問題,首次利用目標(biāo)的空間時頻分布矩陣代替空間相關(guān)矩陣進(jìn)行陣列校正,并使用蒙特卡洛法仿真分析了不同信噪比下兩種方法的校正結(jié)果,最后使用該方法對實際數(shù)據(jù)進(jìn)行處理,驗證了該方法在實際應(yīng)用中的效果。

1 理論部分

1.1 陣列的幅相誤差模型

假設(shè)天線陣為圖1所示的M元均勻線陣,目標(biāo)信號源來自方位角θ,則第m(m=1,2,…,M)個陣元接收到的信號為

式中:xm(t)表示目標(biāo)信號;nm(t)表示加性噪聲;ym(t)=ejτms(t),τm為信號到第m個陣元的入射時延。以第一個陣元為參考陣元,τm可寫成:

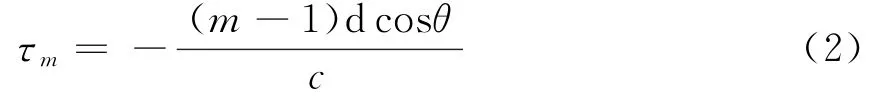
均勻線陣無法測目標(biāo)的俯仰角,因此此處不再考慮俯仰角;c表示電磁波的傳播速度。

圖1 均勻線陣

將陣列的幅相誤差考慮在內(nèi),陣元的接收信號可改寫成:

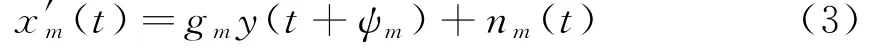
式中:gm表示第m個陣元的幅度誤差;ψm表示陣元m上的等效信號時延誤差。寫成矩陣形式為

式中:Γ=diag{g1ejφ1,g2ejφ2,…,gMejφM},g與φ分別表示各陣元的幅度與相位誤差;X(t)=[x1(t),x2(t),…,xM(t)]T,X′(t)=[x′1(t),x′2(t),…,x′M(t)]T,T表示轉(zhuǎn)置。

1.2 空間時頻分布矩陣

空間時頻分布(STFD)的定義式為

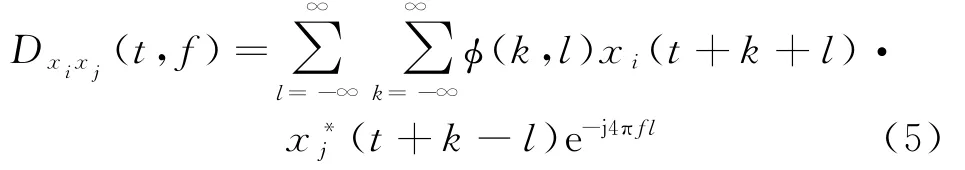
式中:?(k,l)表示時頻核,k與f分別表示時間參量與頻率參量;i與j表示矩陣的行和列,且i,j=1,2,…,M;xi與xj表示不同陣元接收到同一信源的數(shù)據(jù);符號?代表共軛運算。將STFD寫成矩陣形式為

將式(1)代入式(5),DXX展開為如下形式:

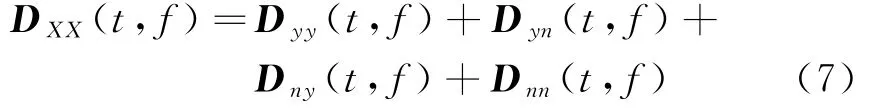
由假設(shè)條件,噪聲與信源獨立可知

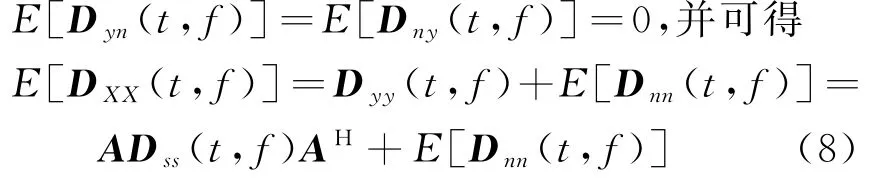
式中:A表示信源X在θ方向的導(dǎo)向矢量;E[·]表示期望運算。將式(4)代入式(8)可得

在實際數(shù)據(jù)處理中,可取多個時頻點,通過下式估計出目標(biāo)信號的STFD矩陣:

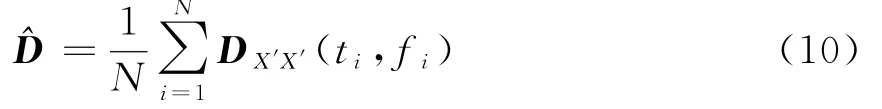
式中,N為時頻點個數(shù)。

1.3 STFD信噪比提升分析

設(shè)時頻窗寬度為L,xi(t)=Wiejwi(t),則時頻矩陣的對角線第i個元素如下式所示:

式中,Wi表示第i個信號的幅度,wi(t)表示其相位。則沿著時頻點的第i個信號的瞬時頻率為

并且wi(t+υ)-wi(t-υ)-4πfi(t)υ≈0,有下式成立:

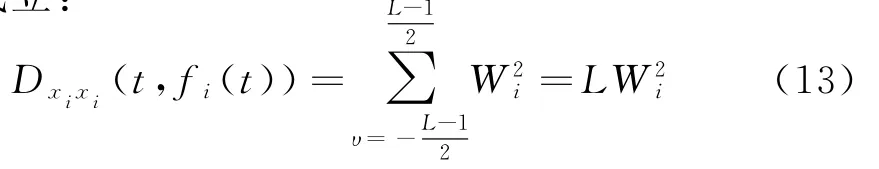
類似地,噪聲的空時分布為

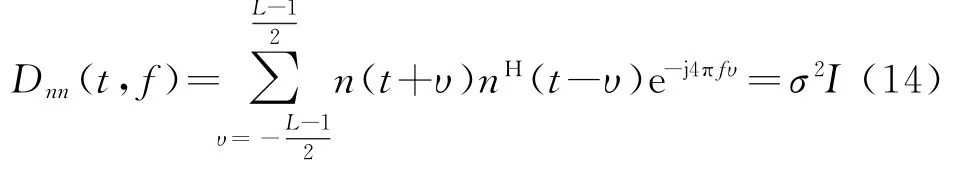
式中,σ2表示白噪聲功率,I表示單位對角陣。由此可以看出,沿信號瞬時頻率選擇時頻點,可以有效地將信噪比增強L倍。

1.4 陣列的幅相誤差校正方法

文獻(xiàn)[12-13]中提出了一種陣列校正的新方法,主要利用空間相關(guān)矩陣中元素相位線性變化的規(guī)律,運用曲線擬合等方法估計出陣列的相位誤差。本文擬使用空間時頻矩陣代替空間相關(guān)矩陣對相位和幅度誤差進(jìn)行估計。相位誤差估計公式如下:式中:?m,1為^D的相位矩陣Φ的第m行、第1列的元素;^α為估計出的^D的相位變化斜率。

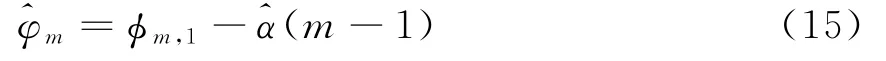
陣列的幅度誤差可由STFD矩陣的主對角元素進(jìn)行估計。由式(9)易知:

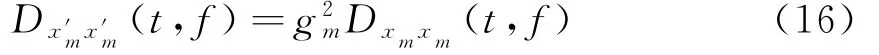
當(dāng)信噪比較高時,Dxmxm(t,f)=Dx1x1(t,f)。以第一陣元為參考陣元,可估計出各陣元的相對幅度誤差^gm為

2 仿真分析

使用蒙特卡洛法,在不同信噪比下,仿真對比空間時頻分布矩陣STFD與空間相關(guān)矩陣SCM的陣列校正效果。

仿真實驗中,設(shè)定陣元數(shù)目為16,目標(biāo)信號的來波方向為20°,蒙特卡洛循環(huán)次數(shù)為100,每次實驗的幅相誤差由式(18)、(19)隨機產(chǎn)生:

式中:βm和ηm為[-0.5,0.5]上的均勻分布;σg為幅度誤差方差,σφ為相位誤差方差。每個陣元的平均求解誤差由下式得到:

式中:Γi表示每次蒙特卡洛實驗隨機產(chǎn)生的幅相誤差矩陣;^Γi表示校準(zhǔn)算法估計出的誤差矩陣;N表示蒙特卡洛實驗次數(shù);mean(·)表示對矩陣(·)求平均。

圖2是在σg=0.5,σφ=15的情況下,不同信噪比時每個陣元的平均誤差。可以看出,基于STFD矩陣求解陣列幅相誤差比傳統(tǒng)利用空間相關(guān)矩陣對信噪比的要求降低了5 d B左右。這主要是因為通過時頻點的選取濾除了大部分噪聲,降低了噪聲功率,從而提高了信噪比。另外,當(dāng)信噪比高于15 dB之后,兩種校正效果大致相同。圖3為在SNR=0,σg=0.5的情況下,通過改變σφ獲得的實驗結(jié)果。同樣可以看出,在誤差容忍度不變的情況下,基于STFD矩陣陣列校正能力提高了10°左右的校正能力。

文獻(xiàn)[14-15]中已經(jīng)給出了幅相誤差對雷達(dá)性能的影響。其中最主要的影響在于接收陣旁瓣水平的提高,因此本文將通過對比校正前后的旁瓣水平來估計校正效果。獲得最小平均旁瓣所需的權(quán)值為

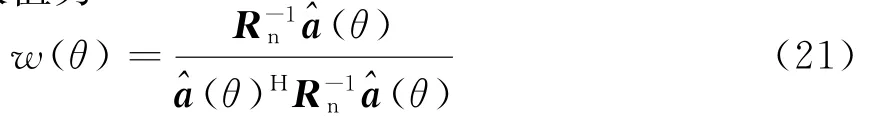
式中,^a(θ)為校正后的陣列導(dǎo)向矢量,Rn為噪聲的相關(guān)矩陣。對于方向θ的波束形成為

式中,θ為波束方向,?為目標(biāo)方向。使用式(22)即可計算出旁瓣水平。圖4展示的是在信噪比為10 d B時通過蒙特卡洛實驗獲得的陣列旁瓣峰值水平。從圖中可以看出,校正后旁瓣普遍降低了5 dB以上,而且使用STFD矩陣相較于傳統(tǒng)SCM方法,旁瓣再次降低3 dB左右,而且更加趨近于無幅相誤差時的旁瓣水平。

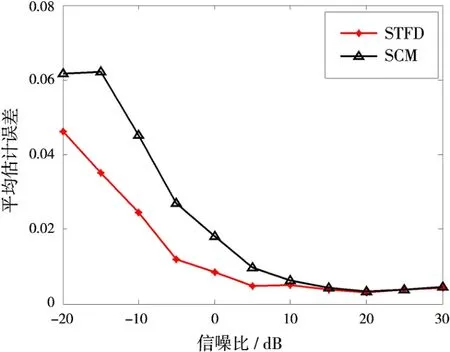
圖2 不同信噪比下的對比

圖3 不同相位誤差情況下的對比

圖4 旁瓣峰值水平

3 實測數(shù)據(jù)處理

本文采用的雷達(dá)數(shù)據(jù)來自于哈工大(威海)高頻地波雷達(dá)站,接收陣為8元均勻線陣,相干積累周期150 s,距離分辨單元1.5 km,有效距離門個數(shù)194。由于高頻地波雷達(dá)常以積累周期作為數(shù)據(jù)處理的基本時間單位,因此本文也以此為單位進(jìn)行陣列校正。取第一個陣元一個積累周期的數(shù)據(jù),作距離多普勒變換,得到圖5所示的R-D譜。

圖6為第80個距離門的剖面圖,可以看到在120 km處有一個速度為-6 m/s的目標(biāo)。圖7為使用W-V分布做出的時頻分布圖,可以看到在Doppler對應(yīng)位置有圖6所示目標(biāo),并顯示出該目標(biāo)的即時速度。

對圖7中[300～600,-6.5～-7.5]之間的300個譜進(jìn)行譜峰搜索可得到300個時頻點。對這些時頻點利用式(9)可得300個STFD矩陣,最后利用式(10)即可得到STFD矩陣的估計值^D。將^D運用到上文中的校正算法中,便可獲得該積累周期的幅相誤差,結(jié)果如圖8所示。圖9為使用該結(jié)果校正前后目標(biāo)常規(guī)波束形成的空間譜對比,可以看到校正前后旁瓣水平下降,并且由STFD進(jìn)行陣列校正的效果優(yōu)于傳統(tǒng)SCM方法。

圖5 第一陣元的R-D譜

圖6 第80距離門的剖面圖

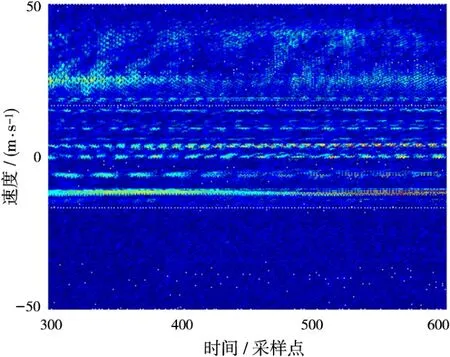
圖7 103距離門一個積累周期的時頻分布圖

圖8 陣列幅相誤差值

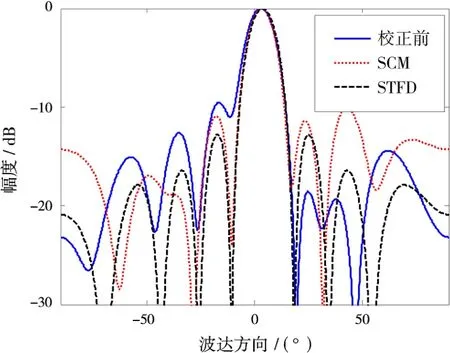
圖9 目標(biāo)常規(guī)波束形成空間譜

4 結(jié)束語

本文提出了一種使用空間時頻分布矩陣代替?zhèn)鹘y(tǒng)的空間相關(guān)矩陣,對高頻地波雷達(dá)接收陣列的幅相誤差進(jìn)行校正的新方法。相比傳統(tǒng)基于SCM的陣列校正方法,本文提出的新方法對信噪比低于15 dB情況下校正效果改善尤為明顯,大大提高了接收陣列校正的適應(yīng)范圍,具有一定的實際應(yīng)用價值。通過計算機仿真和實際數(shù)據(jù)檢驗,驗證了該方法的有效性。但是,使用STFD進(jìn)行陣列校正時,時頻點的選取較為困難,而且由于所需STFD矩陣數(shù)量較多,其計算量也比傳統(tǒng)方法要大。因此,如何快捷、準(zhǔn)確地選取合適的時頻點,以及如何降低STFD算法的計算量,將是后續(xù)研究的重點。

[1]李曉東,于長軍,陳磊,等.一種用于高頻雷達(dá)探測性能評估的方法[J].雷達(dá)科學(xué)與技術(shù),2015,13(6):587-591.

LI Xiaodong,YU Changjun,CHEN Lei,et al.A Method for Detection Performance Evaluation of High Frequency Surface Wave Radar[J].Radar Science and Technology,2015,13(6):587-591.(in Chinese)

[2]BRUNO L,BRACA P,HORSTMANN J,et al.Experimental Evaluation of the Range-Doppler Coupling on HF Surface Wave Radars[J].IEEE Geoscience and Remote Sensing Letters,2013,10(4):850-854.

[3]SCHMID C M,SCHUSTER S,FEGER R,et al.On the Effects of Calibration Errors and Mutual Coupling on the Beam Pattern of an Antenna Array[J].IEEE Trans on Antennas and Propagation,2013,61(8):4063-4072.

[4]CAI W,XIE J,SUN M.Space-Time Distribution of the First-Order Sea Clutter in High Frequency Surface Wave Radar on a Moving Shipborne Platform[C]∥Fifth International Conference on Instrumentation and Measurement,Computer,Communication and Control,Qinhuangdao:IEEE,2015:1408-1412.

[5]WEISS C,ZOUBIR A M.Robust High-Resolution DOA Estimation with Array Pre-Calibration[C]∥22nd European Signal Processing Conference,Lisbon:IEEE,2014:1049-1052.

[6]龍超.高頻地波雷達(dá)陣列優(yōu)化與校正算法研究[D].武漢:武漢大學(xué),2012:83-90.

[7]PAULRAJ A,KAILATH T.Direction of Arrival Estimation by Eigenstructure Methods with Unknown Sensor Gain and Phase[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,Tampa,FL:IEEE,1985:640-643.

[8]WEISS A J,FRIEDLANDER B.Array Shape Calibration Using Sources in Unknown Locations:A Maximum Likelihood Approach[C]∥International Conference on Acoustics,Speech and Signal Processing,New York:IEEE,1988:2670-2673.

[9]FRIEDLANDER B,WEISS A J.Eigenstructure Methods for Direction Finding with Sensor Gain and Phase Uncertainties[C]∥International Conference on Acoustics,Speech and Signal Processing,New York:IEEE,1988:2681-2684.

[10]于文啟,陳建文,楊春山.一種天波超視距雷達(dá)電離層相位污染的校正算法[J].雷達(dá)科學(xué)與技術(shù),2015,13(6):660-666.

YU Wenqi,CHEN Jianwen,YANG Chunshan.A Correction Algorithm for Ionopheric Phase Contamination in Sky-Wave Over-the-Horizon Radar[J].Radar Science and Technology,2015,13(6):660-666.(in Chinese)

[11]AMIN M G,ZHANG Y.Direction Finding Based on Spatial Time-Frequency Distribution Matrices[J].Digital Signal Processing,2000,10(4):325-339.

[12]SONG Xiaoguo,WEI Yinsheng,CUI Yan,et al.A Novel Array Calibration Method Based on Spatial Correlation Matrix for HFSWR[C]∥10th International Conference on Signal Processing,Beijing:IEEE,2010:344-347.

[13]WEI Yinsheng,SONG Xiaoguo,TAN Jiubin.An Array Calibration Method Using Spatial Correlation Properties for HFSWR[C]∥CIE International Conference on Radar,Chengdu:IEEE,2011:364-367.

[14]SOLOMONI S D,ABRAMOVICH Y I,GRAY D A.OTH Radar Antenna Array Calibration Analysis[C]∥4th International Symposium on Signal Processing and Its Applications,Gold Coast:IEEE,1996:471-474.

[15]SOLOMON I S D,GRAY D A,ABRAMOVICH Y I,et al.Receiver Array Calibration Using Disparate Sources[J].IEEE Trans on Antennas and Propagation,1999,47(3):496-505.