兩級(jí)行星齒輪傳動(dòng)非線性嚙合力頻率耦合與動(dòng)態(tài)特性研究
兩級(jí)行星齒輪傳動(dòng)非線性嚙合力頻率耦合與動(dòng)態(tài)特性研究
劉輝1,2,蔡仲昌3,項(xiàng)昌樂1,2
(1.北京理工大學(xué)機(jī)械與車輛學(xué)院,北京100081; 2.北京電動(dòng)車輛協(xié)同創(chuàng)新中心,北京100081;3.中國(guó)航天三江集團(tuán)特種車輛技術(shù)中心,武漢430023)
摘要:利用拉格朗日方程推導(dǎo)了兩級(jí)行星齒輪傳動(dòng)的平移-扭轉(zhuǎn)非線性振動(dòng)模型,模型考慮了齒側(cè)間隙、時(shí)變嚙合剛度及其相位差、綜合嚙合誤差、行星輪位置角時(shí)變性以及各行星排級(jí)間連接件的彎曲和扭轉(zhuǎn)剛度。從行星排級(jí)間連接軸的力與變形耦合關(guān)系出發(fā),研究了兩個(gè)行星排嚙合力產(chǎn)生的嚙合頻率耦合現(xiàn)象。通過數(shù)值仿真對(duì)不同激勵(lì)條件下嚙合頻率耦合的表現(xiàn)形式進(jìn)行了研究,對(duì)不同行星排的動(dòng)載系數(shù)、均載系數(shù)、連接軸轉(zhuǎn)矩的動(dòng)態(tài)特性進(jìn)行了分析,為多級(jí)行星齒輪傳動(dòng)系統(tǒng)動(dòng)力學(xué)分析與設(shè)計(jì)提供指導(dǎo)。
關(guān)鍵詞:行星齒輪傳動(dòng);非線性;嚙合力;嚙頻耦合;動(dòng)載系數(shù);均載系數(shù)
中圖分類號(hào):TH132.41; TB123
文獻(xiàn)標(biāo)志碼:A
DOI:10.13465/j.cnki.jvs.2015.19.003
Abstract:Based on Lagrange’s equation, the translational-torsional coupled nonlinear dynamic model of two stage planetary gears was established considering backlash, time-varying mesh stiffness and its phase difference, gear mesh composite errors, time-varying planet wheel position angle, and torsional and bending stiffnesses of connectors among different stages. According to the relationship among torques of connection shafts and vibration displacements of parts, the meshing frequency coupling phenomenon of mesh force for different stages was studied. Under different excitation conditions, the forms of meshing frequency coupling were analyzed. At the same time, the dynamic load coefficient and the load sharing coefficient of meshing force for different stages, and the dynamic characteristics of torques of connection shafts were calculated. The results provided a reference for design and dynamic analysis of multi-stage planetary gears.
基金項(xiàng)目:國(guó)家自然科學(xué)基金(11232003, 91315302); 國(guó)家基礎(chǔ)性發(fā)展規(guī)劃項(xiàng)目(2010CB832704); 國(guó)家高技術(shù)研究發(fā)展計(jì)劃(2012AA050901)資助; 教育部博士點(diǎn)基金(20130041110050)
收稿日期:2014-06-30修改稿收到日期:2014-10-17
Frequency coupling and dynamic characteristics of nonlinear meshing force for two-stage planetary gears
LIUHui1,2,CAIZhong-chang3,XIANGChang-le1,2(1. School of Mechanical and Engineering, Beijing Institute of Technology, Beijing 100081, China;2. Collaborative Innovation Center of Electric Vehicles in Beijing, Beijing 100081, China;3. Special Vehicle Technology Center of China Space Sanjiang Group, Wuhan 430023, China)
Key words:planetary gears; nonlinear; meshing force; meshing frequency coupling; dynamic load coefficient; load sharing coefficient
多級(jí)行星齒輪傳動(dòng)在車輛、船舶、航空、風(fēng)力發(fā)電、工程機(jī)械等各種工業(yè)領(lǐng)域的傳動(dòng)系統(tǒng)中得到了廣泛應(yīng)用。在動(dòng)態(tài)條件下,當(dāng)動(dòng)力在各級(jí)行星排中傳遞時(shí),振動(dòng)也在不同行星排、不同部件之間傳遞并相互影響,造成各行星排之間動(dòng)力學(xué)的耦合。目前研究以單級(jí)行星齒輪傳動(dòng)為主,多級(jí)行星齒輪傳動(dòng)振動(dòng)特性研究尚不夠深入,分析行星排級(jí)間耦合原因和表現(xiàn)形式是研究多級(jí)行星齒輪傳動(dòng)振動(dòng)特性區(qū)別于單級(jí)行星傳動(dòng)的一個(gè)重要內(nèi)容。
近幾十年來,國(guó)內(nèi)外學(xué)者對(duì)多級(jí)行星齒輪動(dòng)力學(xué)開展了許多有益的研究。Kahraman[1]建立了用于功率流分析的行星傳動(dòng)系統(tǒng)轉(zhuǎn)速轉(zhuǎn)矩分析模型。Deur等[2]建立了包含離合器摩滑過程控制模型的某車輛行星傳動(dòng)系統(tǒng)動(dòng)力學(xué)模型。Kiracofer[3]、Kahraman[4]、Guo[5-6]、李瑰賢[7]、蔡仲昌[8]各自針對(duì)不同形式的多級(jí)行星傳動(dòng)對(duì)固有振動(dòng)的建模方法、振動(dòng)模式特點(diǎn)、參數(shù)靈敏度特性進(jìn)行了研究。Inalpolat等[9-10]在線性振動(dòng)范圍內(nèi)分析了車輛多級(jí)行星傳動(dòng)在不同擋位下的共振轉(zhuǎn)速和振幅響應(yīng)。秦大同等[11-12]研究了盾構(gòu)機(jī)三級(jí)行星齒輪減速器在外部激勵(lì)作用下構(gòu)件振動(dòng)位移和動(dòng)態(tài)嚙合力的動(dòng)態(tài)響應(yīng)和頻譜特性。Al-shyyab等[13]采用一種改進(jìn)的諧波平衡法推導(dǎo)了兩級(jí)行星齒輪傳動(dòng)純扭模型的半解析解,并研究了系統(tǒng)非線性響應(yīng)特性。朱自冰等[14]研究了兩級(jí)星型齒輪傳動(dòng)的非線性振動(dòng)響應(yīng)以及分岔、混沌特性。孫智民等[15]研究了兩級(jí)輪系組成的封閉行星齒輪傳動(dòng)的嚙合力動(dòng)載荷特性和中心輪浮動(dòng)軌跡。劉輝等[16-17]建立了多間隙、多時(shí)變參數(shù)的單級(jí)行星傳動(dòng)非線性動(dòng)力學(xué)模型,研究了其在不同外界激勵(lì)條件下嚙合力、扭振角位移的頻譜特性。目前有關(guān)多級(jí)行星齒輪傳動(dòng)的動(dòng)力學(xué)研究以振動(dòng)響應(yīng)特性為主,對(duì)行星排之間動(dòng)力學(xué)耦合特性的研究還不夠深入。
本文以兩級(jí)受載行星傳動(dòng)非線性振動(dòng)模型為基礎(chǔ),分析了兩個(gè)受載行星排之間嚙合力在頻域內(nèi)產(chǎn)生耦合的原因,對(duì)定值驅(qū)動(dòng)轉(zhuǎn)矩和單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩作用下兩個(gè)行星排的嚙合力進(jìn)行了頻譜特性分析,研究了嚙合頻率耦合現(xiàn)象的各種存在形式。對(duì)不同行星排嚙合力的動(dòng)載特性、均載特性、連接軸轉(zhuǎn)矩動(dòng)態(tài)特性進(jìn)行了分析,為車輛行星齒輪傳動(dòng)動(dòng)態(tài)性能分析與設(shè)計(jì)提供了參考。
1動(dòng)力學(xué)建模
1.1模型描述與假設(shè)
本文研究對(duì)象是車輛自動(dòng)變速箱中常用的一種兩級(jí)行星傳動(dòng),其結(jié)構(gòu)簡(jiǎn)圖見圖1。系統(tǒng)有兩個(gè)普通行星排,每個(gè)行星排包含四個(gè)行星輪,動(dòng)力從一排太陽輪軸輸入,從二排行星架輸出。當(dāng)一排齒圈制動(dòng)時(shí),兩個(gè)行星排都處于受載狀態(tài)。
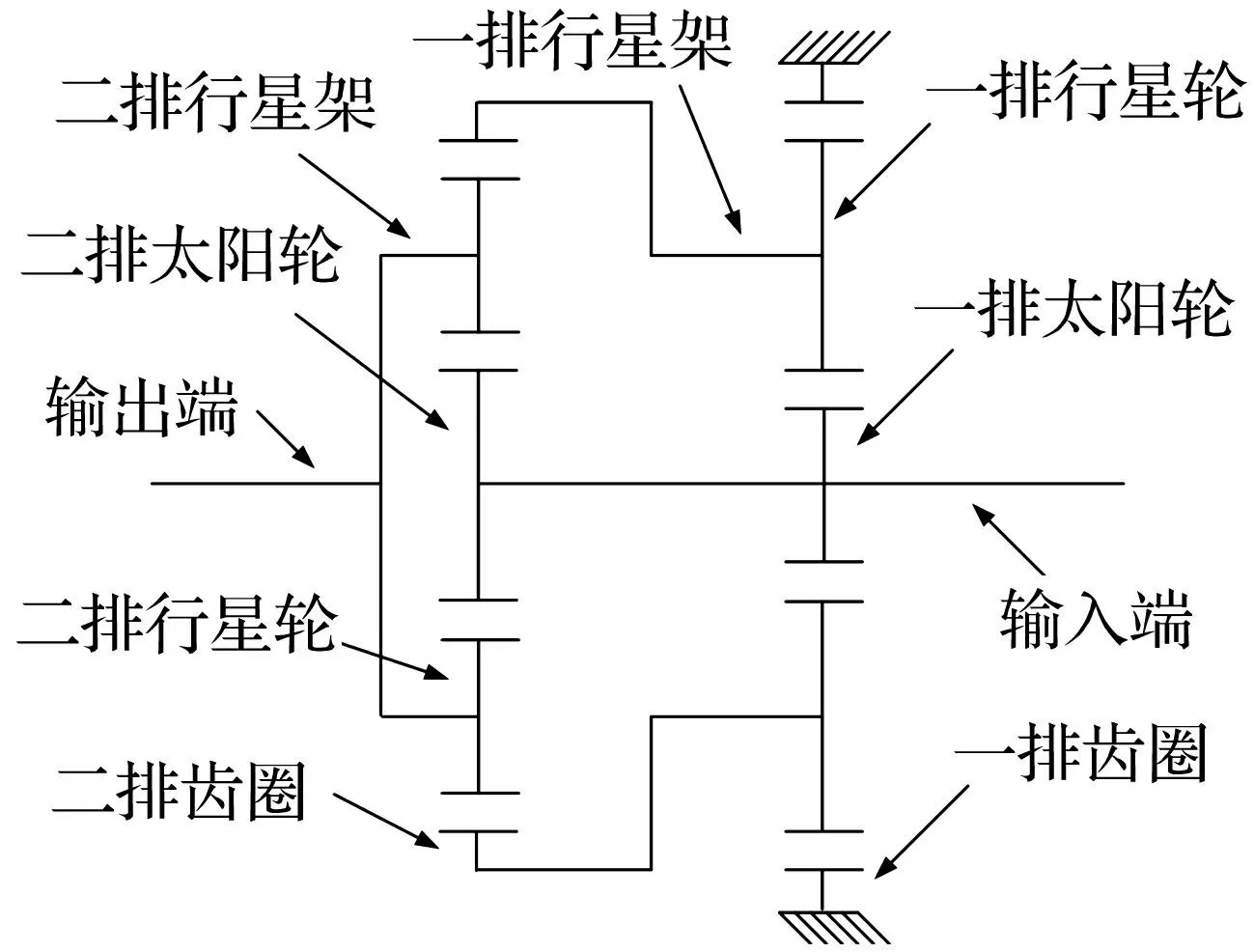
圖1 行星傳動(dòng)簡(jiǎn)圖 Fig.1 Sketch map of planetary transmission
本文采用以統(tǒng)一固定參考系為基準(zhǔn)的方法描述各部件振動(dòng)位移。對(duì)于中心旋轉(zhuǎn)部件,直接采用固定參考系下的絕對(duì)位移描述其平移運(yùn)動(dòng)和旋轉(zhuǎn)運(yùn)動(dòng);對(duì)于行星輪,其固定參考系中的絕對(duì)運(yùn)動(dòng)分解為與行星架同步運(yùn)動(dòng)的動(dòng)坐標(biāo)系的牽連運(yùn)動(dòng)和相對(duì)于該動(dòng)坐標(biāo)系的相對(duì)運(yùn)動(dòng)的矢量和。該描述方法在一個(gè)統(tǒng)一的固定參考系中進(jìn)行動(dòng)力學(xué)分析,避免了不同旋轉(zhuǎn)參考系間的坐標(biāo)轉(zhuǎn)換。
本文采用集中參數(shù)法建模,采用如下假設(shè):
(1)軸承剛度、制動(dòng)件切向支承剛度、行星排連接件剛度均為線性,行星排連接件具有扭轉(zhuǎn)和彎曲彈性,齒輪本體、行星架、行星輪軸為剛體;
(2)忽略嚙合線方向由于齒輪軸系振動(dòng)引起的瞬態(tài)變化,嚙合力的方向始終沿著嚙合線方向;
(3)每個(gè)部件有三個(gè)自由度,分別是在垂直于自身旋轉(zhuǎn)軸線的平面內(nèi)的平移振動(dòng)和繞自身旋轉(zhuǎn)軸線的扭轉(zhuǎn)振動(dòng);
(4)各行星輪沿行星架圓周方向均勻分布,其質(zhì)量、慣量、誤差、支撐剛度等參數(shù)均相同;
(5)系統(tǒng)阻尼與部件的相對(duì)運(yùn)動(dòng)速度成正比。
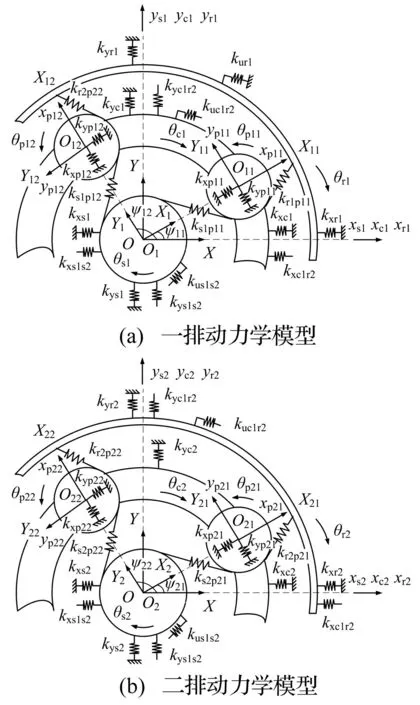
圖2 兩級(jí)行星齒輪傳動(dòng)動(dòng)力學(xué)模型 Fig.2 The dynamic model of two stage planetary transmission
兩級(jí)行星傳動(dòng)中各行星排的集中參數(shù)模型如圖2所示。圖中OXY為系統(tǒng)公用的固定坐標(biāo)系,OiXiYi為第i級(jí)行星排自己的旋轉(zhuǎn)坐標(biāo)系,OijXijYij為第i級(jí)行星排中第j個(gè)行星輪的坐標(biāo)系。下標(biāo)si、ri、ci、pij分別為第i級(jí)太陽輪、齒圈、行星架以及第i級(jí)中第j個(gè)行星輪。xa、ya、θa分別為部件a在各自相關(guān)坐標(biāo)系中沿橫、縱坐標(biāo)軸的微小平移位移以及繞該坐標(biāo)原點(diǎn)旋轉(zhuǎn)軸的微小角位移,a=si、ri、ci、pij。太陽輪、齒圈、行星架的微小振動(dòng)位移是相對(duì)固定參考系的絕對(duì)運(yùn)動(dòng)量,行星輪的微小振動(dòng)位移是相對(duì)行星架旋轉(zhuǎn)參考系的相對(duì)運(yùn)動(dòng)量。ksipij、csipij、bsipij分別為第i級(jí)行星排中太陽輪和第j個(gè)行星輪之間輪齒的時(shí)變嚙合剛度、嚙合阻尼、齒側(cè)間隙一半,kripij、cripij、bripij的含義與此類似,不再贅述。kur1為第1級(jí)齒圈沿旋轉(zhuǎn)方向的切向支承剛度,kxa、kya為各部件在各自坐標(biāo)系中沿橫、縱坐標(biāo)軸的軸承支承剛度,kxhiql、kyhiql、kuhiql為第i級(jí)行星排中部件h與第l級(jí)行星排中部件q的連接件的彎曲剛度和扭轉(zhuǎn)剛度,i、l為整數(shù),i≠l;h、q=s,r,c。ψij為第i級(jí)行星排中第j個(gè)行星輪在固定坐標(biāo)系中的位置角,ψij=ωcit+2π(j-1)/n,n為第i級(jí)中行星輪個(gè)數(shù)。Ja、ma、Ra分別為部件a的轉(zhuǎn)動(dòng)慣量、質(zhì)量、等效半徑。α為壓力角。
綜合嚙合誤差是隨時(shí)間變化的函數(shù),由制造誤差、安裝誤差、齒形誤差組成。各誤差在內(nèi)、外嚙合線上產(chǎn)生的當(dāng)量累積嚙合誤差為
(1)
式中:Ea、Aa分別為各部件制造誤差幅值、安裝誤差幅值,Esipij、Eripij分別為各嚙合副的齒形誤差幅值,ωa分別為各部件理論角速度,ωmi、Ti分別為第i級(jí)行星排的嚙合頻率、嚙合周期,βa、γa分別為各誤差的相位角,γsipij、γripij為各行星輪外、內(nèi)嚙合副之間的嚙合相位差,γsri為同一個(gè)行星輪上外嚙合副與內(nèi)嚙合副之間的嚙合相位差,t為時(shí)間。
時(shí)變嚙合剛度通常假設(shè)為周期矩形波,它們之間的相位差計(jì)算方法見文獻(xiàn)[18]。將時(shí)變嚙合剛度展成Fourier級(jí)數(shù),取六次諧波項(xiàng)時(shí)其表達(dá)式為
(2)
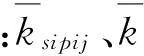
嚙合阻尼較為復(fù)雜,其影響因素很多,不易準(zhǔn)確求得,本文采用的嚙合阻尼經(jīng)驗(yàn)公式為
(3)
式中:ma為各齒輪等效質(zhì)量,ζ為阻尼比,取為0.07。
齒側(cè)間隙是輪齒嚙合力描述中的強(qiáng)非線性項(xiàng),齒側(cè)間隙非線性函數(shù)f的表達(dá)式為
(4)
式中:Lsipij為嚙合線變形量,bsipij為單邊齒側(cè)間隙。內(nèi)嚙合情況與此類似。
各外、內(nèi)嚙合線變形量Lsipij、Lripij包括各部件扭轉(zhuǎn)振動(dòng)、平移振動(dòng)引起的線位移變形量和綜合嚙合誤差引起的等效變形量,其表達(dá)式為
(5)
式中:Ra為各部件的等效半徑。
第i級(jí)行星排第j個(gè)行星輪與太陽輪、齒圈在各自嚙合線上的嚙合力Fsipij、Fripij分別為
(6)
各部件的軸承支反力Fxa、Fya為
(7)
一排太陽輪與二排太陽輪連接軸的扭轉(zhuǎn)轉(zhuǎn)矩Ts1s2和彎曲平面內(nèi)的橫向力Fxs1s2、Fys1s2為
(8)
一排行星架與二排齒圈連接軸的扭轉(zhuǎn)轉(zhuǎn)矩Tc1r2和彎曲平面內(nèi)的橫向力Fxc1r2、Fyc1r2為
(9)
發(fā)動(dòng)機(jī)波動(dòng)轉(zhuǎn)矩是車輛行星傳動(dòng)的動(dòng)力來源,本文中發(fā)動(dòng)機(jī)為V型12缸4沖程柴油機(jī),通過簡(jiǎn)諧分析得出主要諧次[17],為對(duì)比分析發(fā)動(dòng)機(jī)轉(zhuǎn)矩波動(dòng)對(duì)系統(tǒng)響應(yīng)的影響,將驅(qū)動(dòng)轉(zhuǎn)矩劃分為定值驅(qū)動(dòng)轉(zhuǎn)矩、單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩兩種,其表達(dá)式分別為
Tin=T0
(10)
Tin=T0+μT0sin(2πfet+φe)
(11)
式中:T0為發(fā)動(dòng)機(jī)輸出轉(zhuǎn)矩平均值,fe為發(fā)動(dòng)機(jī)波動(dòng)轉(zhuǎn)矩頻率,取為曲軸6倍轉(zhuǎn)頻,φ為波動(dòng)轉(zhuǎn)矩的初始相位,μ為波動(dòng)轉(zhuǎn)矩幅值與平均值之比,取0.3。
本文采用定步長(zhǎng)四階Runge-Kutta法求解系統(tǒng)非線性方程組的數(shù)值解,系統(tǒng)主要參數(shù)如表1~表3所示。
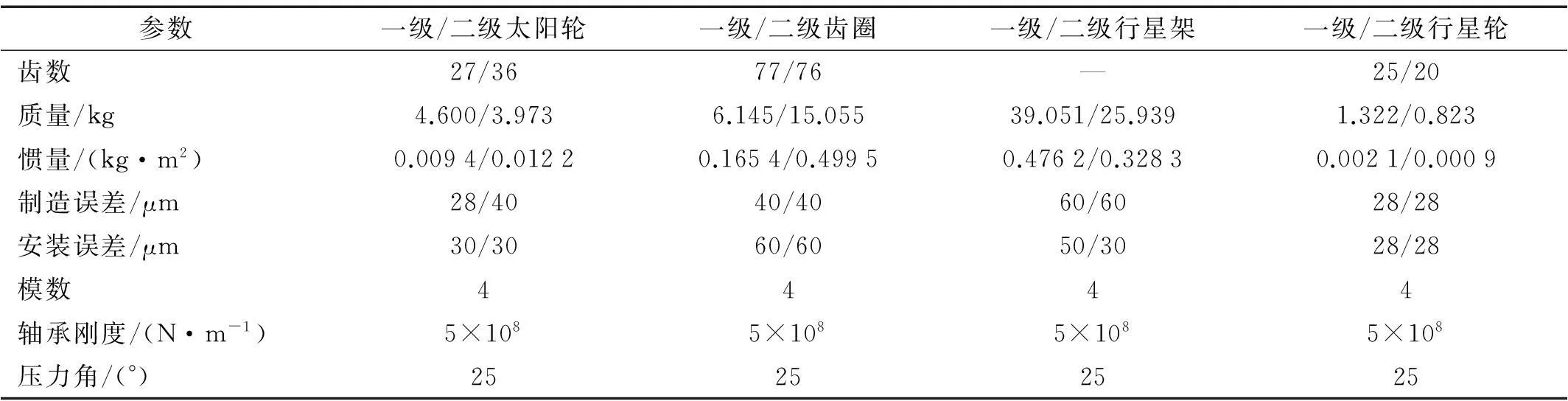
表1 兩級(jí)行星傳動(dòng)系統(tǒng)主要參數(shù)

表2 兩級(jí)行星傳動(dòng)系統(tǒng)嚙合剛度和齒形制造誤差

表3 兩級(jí)行星傳動(dòng)系統(tǒng)彎曲剛度和扭轉(zhuǎn)剛度
1.3動(dòng)力學(xué)模型
將非線性嚙合力和輸入軸驅(qū)動(dòng)轉(zhuǎn)矩視為廣義作用力,根據(jù)Lagrange方程,推導(dǎo)得系統(tǒng)各部件的動(dòng)力學(xué)方程見式(12)至式(19)。
一排太陽輪的振動(dòng)微分方程為
Fxs1+Fbxs1s2=0
(12a)
Fys1+Fbys1s2=0
(12b)
(12c)
一排齒圈的振動(dòng)微分方程為
(13a)
(13b)
(13c)
式中:Tur1為第一排齒圈所受到的制動(dòng)轉(zhuǎn)矩。
一排行星架的振動(dòng)微分方程為
(14a)
(14b)
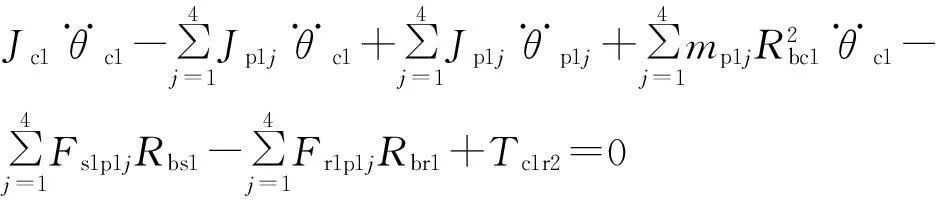
一排行星輪的振動(dòng)微分方程為
sinαFr1p1j+Fxp1j=0
(15a)
cosαFr1p1j+Fyp1j=0
(15b)
(15c)
二排太陽輪的振動(dòng)微分方程為
Fxs2-Fbxs1s2=0
(16a)
Fys2-Fbys1s2=0
(16b)
(16c)
二排齒圈的振動(dòng)微分方程為
Fxr2-Fbxc1r2=0
(17a)
Fyr2-Fbyc1r2=0
(17b)
(17c)
二排行星架的振動(dòng)微分方程為
(18a)
(18b)
(18c)
二排行星輪的振動(dòng)微分方程為
(19a)
(19b)
(19c)
2兩級(jí)行星排嚙合力特性分析
2.1不同行星排嚙合力頻率耦合成因
本文以一排太陽輪與二排太陽輪連接軸為例,從連接軸內(nèi)力與變形耦合關(guān)系出發(fā),說明兩個(gè)行星排嚙合力產(chǎn)生嚙合頻率耦合現(xiàn)象的原因,其耦合過程示意圖見圖3。圖中實(shí)線箭頭為耦合前的嚙合頻率傳遞方向,虛線表示耦合后增加的嚙合頻率傳遞方向。連接軸兩端的太陽輪具有各自不同的振動(dòng)頻率,包括各自轉(zhuǎn)頻、行星排嚙頻、外激勵(lì)頻率以及它們的倍頻。連接軸的扭轉(zhuǎn)內(nèi)力、彎曲內(nèi)力分別把不同頻率的振動(dòng)位移耦合到一起,再以作用力與反作用力的形式分別作用到兩個(gè)被連接部件上。耦合后的被連接部件將含有新頻率的振動(dòng)位移以等效嚙合線變形量的形式反饋回該級(jí)行星排嚙合力,從而造成不同級(jí)行星排嚙合力之間的相互耦合。本文將不同行星排嚙頻及其相關(guān)頻率同時(shí)出現(xiàn)在嚙合力中的耦合振動(dòng)稱為雙嚙頻耦合振動(dòng)現(xiàn)象,相對(duì)于本級(jí)行星排嚙頻而“新”出現(xiàn)的其它級(jí)行星排嚙頻稱為耦合嚙頻。
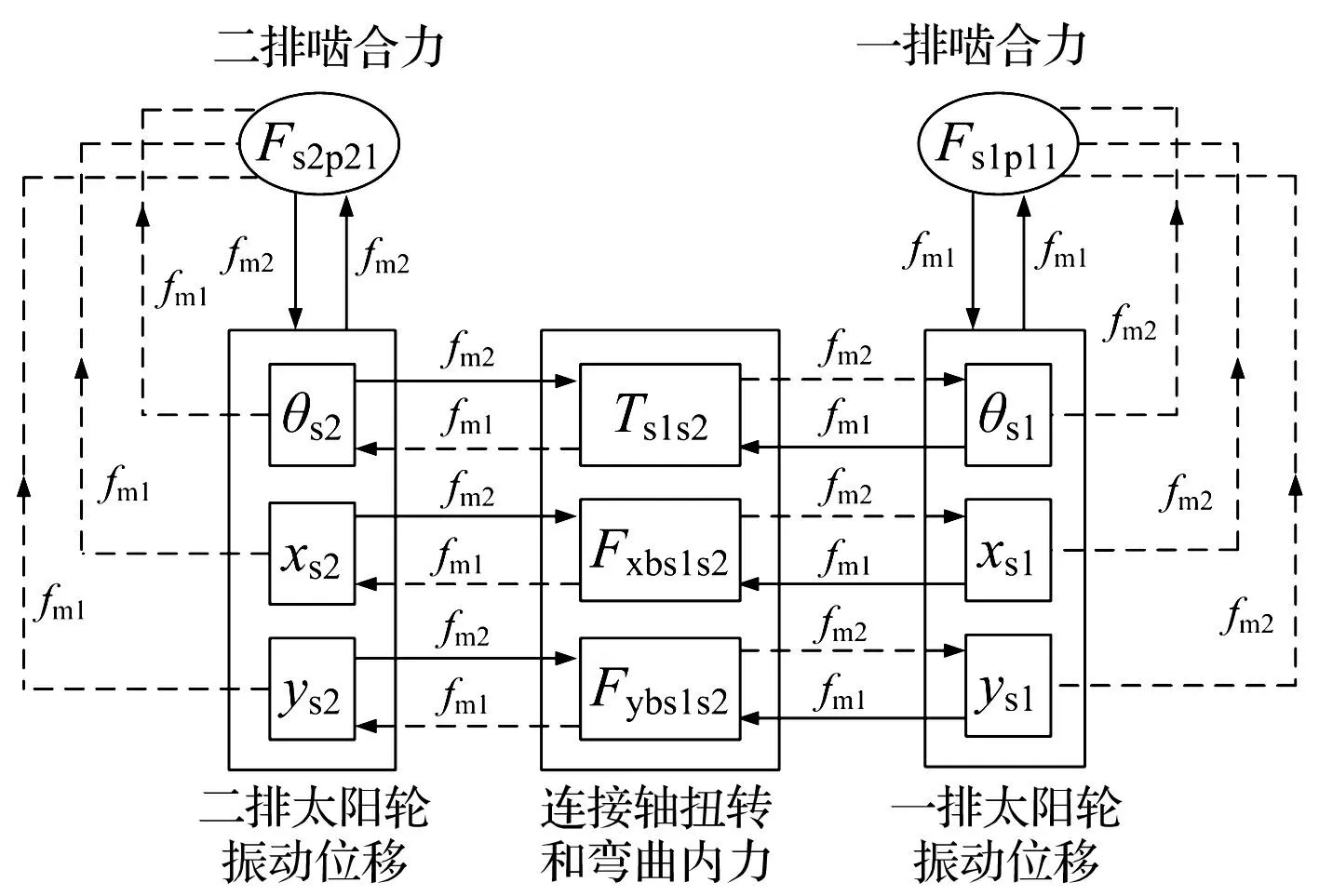
圖3 嚙合力頻率耦合過程示意圖 Fig.3 Schematic diagram of meshing force frequency coupling process
2.2定值驅(qū)動(dòng)轉(zhuǎn)矩時(shí)嚙合力頻譜
T0=500N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖見圖4。與單級(jí)行星排嚙合力的最大區(qū)別是,在一排嚙合力頻譜圖中出現(xiàn)了兩個(gè)二排嚙頻:fm2和2fm2,而在二排嚙合力頻譜圖中一排嚙頻卻只出現(xiàn)在一部分轉(zhuǎn)速中,說明不同行星排嚙合力之間的嚙頻耦合關(guān)系并不是對(duì)等的,其產(chǎn)生的影響是強(qiáng)弱不同的。本文中每個(gè)行星排有四個(gè)外嚙合力和四個(gè)內(nèi)嚙合力,從計(jì)算結(jié)果可以看出,不僅四個(gè)外(內(nèi))嚙合力的頻譜是相似的,而且內(nèi)、外嚙合力的頻譜也是相似的。本文以各級(jí)行星排第一個(gè)行星輪的外嚙合力為例作分析,其他嚙合力的情況類似,限于篇幅不再贅述。
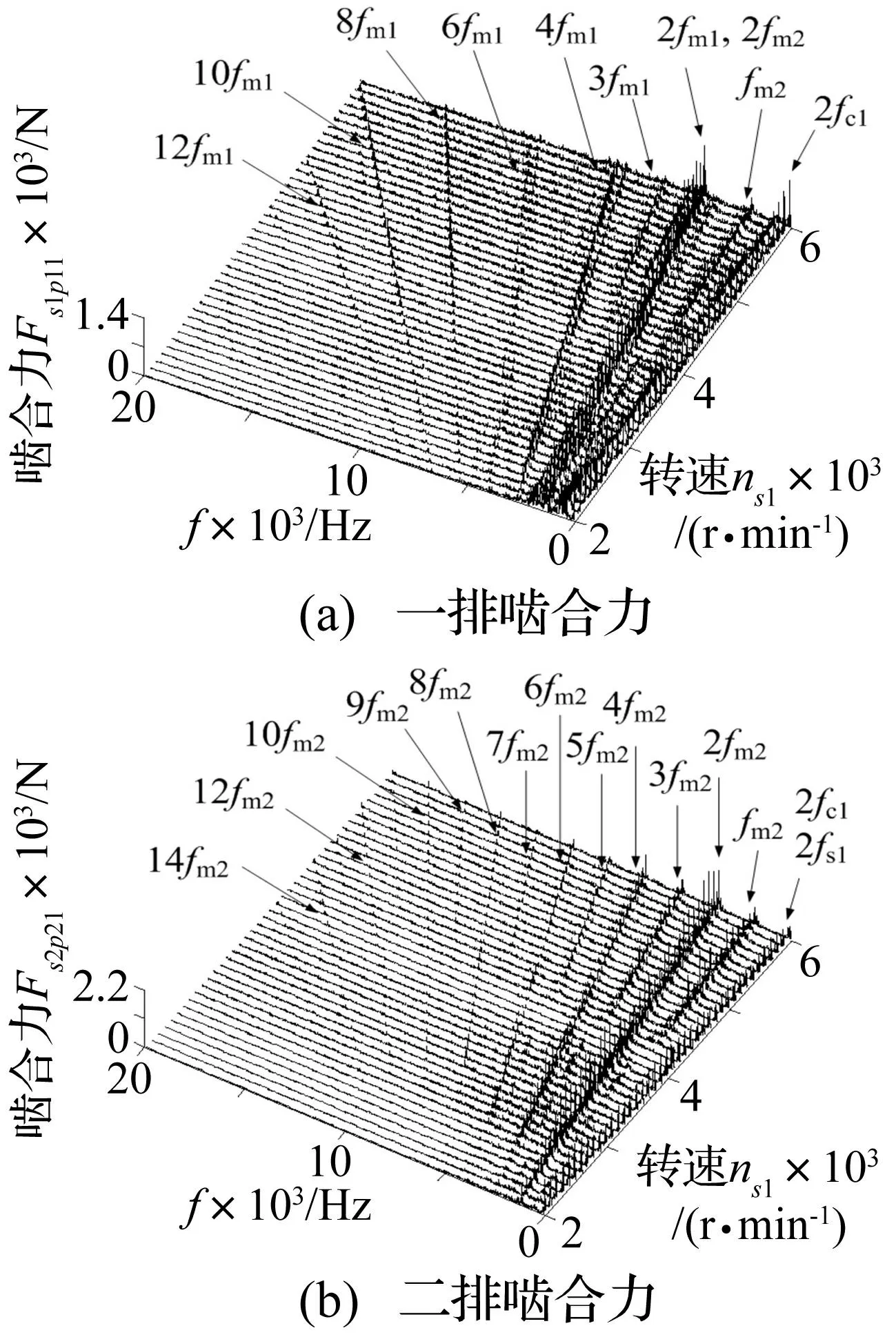
圖4 T 0=500N·m時(shí)定值驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖 Fig.4 The meshing force spectrum waterfall chart under the action of constant torque T 0=500N·m
部分轉(zhuǎn)速下的嚙合力頻譜見圖5和圖6。在一排嚙合力頻譜中,二排嚙頻的存在形式較復(fù)雜,主要有倍頻、分?jǐn)?shù)頻、倍頻與轉(zhuǎn)頻的調(diào)制邊頻、以及二排嚙頻與一排嚙頻的組合頻率,在5000r/min時(shí)存在諸如μfm1+4(fm1-fm2),μ=2,8,10,這樣的復(fù)雜組合形式。在二排嚙合力頻譜中,3000r/min和4000r/min時(shí)沒有出現(xiàn)一排嚙頻,5000r/min時(shí)才出現(xiàn)兩個(gè)一排嚙頻:2fm1和3fm1,說明轉(zhuǎn)速升高引起頻率耦合作用增強(qiáng)。
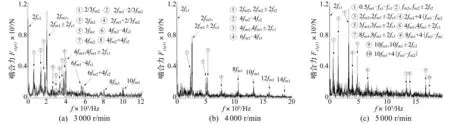
圖5 T 0=500N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的一排嚙合力頻譜圖 Fig.5 The meshing force spectrum of the first planetary under the action of constant torque T 0=500N·m and different rotating speed
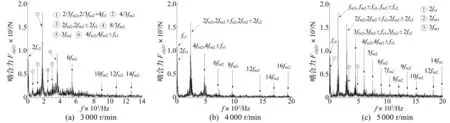
圖6 T 0=500N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的二排嚙合力頻譜圖 Fig.6 The meshing force spectrum of the second planetary under the action of constant torque T 0=500N·m and different rotating speed
T0=2000N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖見圖7。與T0=500N·m時(shí)的區(qū)別是在一排嚙合力頻譜中出現(xiàn)了更高諧次的二排嚙頻:4fm2,在二排嚙合力頻譜中新增了兩個(gè)一排嚙頻:2fm1和4fm1,說明載荷增大也會(huì)導(dǎo)致頻率耦合作用增強(qiáng)。
部分轉(zhuǎn)速下的嚙合力頻譜見圖8和圖9。與T0=500N·m時(shí)相比,耦合嚙頻的存在形式相對(duì)簡(jiǎn)單,但出現(xiàn)了更高諧次的耦合嚙頻,如8倍頻和10倍頻。不同嚙頻的組合形式也發(fā)生改變,μ(fm1+fm2),μ=2,3,成為主要組合形式。
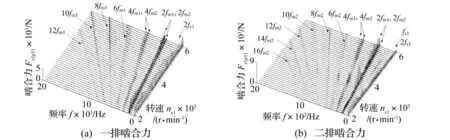
圖7 T 0=2000N·m時(shí)定值驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖 Fig.7 The meshing force spectrum waterfall chart under the action of constant torque T 0=2000N·m

圖8 T 0=2000N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的一排嚙合力頻譜圖 Fig.8 The meshing force spectrum of the first planetary under the action of constant torque T 0=2000N·m and different rotating speed

圖9 T 0=2000N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的二排嚙合力頻譜圖 Fig.9 The meshing force spectrum of the second planetary under the action of constant torque T 0=2000N·m and different rotating speed
2.3單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩時(shí)嚙合力頻譜
T0=500N·m的單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖見圖10。與定值驅(qū)動(dòng)轉(zhuǎn)矩時(shí)的主要區(qū)別是在一排、二排嚙合力頻譜中都沒有明確地出現(xiàn)耦合嚙頻的軌線。當(dāng)時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩平均值較小時(shí),外激勵(lì)頻率和本級(jí)行星排嚙頻是嚙合力的主要頻率,耦合嚙頻的影響是次要的。
T0=500N·m的單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下部分轉(zhuǎn)速的嚙合力頻譜圖見圖11和圖12。與定值驅(qū)動(dòng)轉(zhuǎn)矩時(shí)的主要區(qū)別是,在一排、二排嚙合力頻譜中耦合嚙頻零星分布,其作用十分有限。外激勵(lì)頻率分別與不同行星排嚙頻、各部件轉(zhuǎn)頻發(fā)生調(diào)制關(guān)系。由于二排同時(shí)從太陽輪和齒圈輸入動(dòng)力,且它們都是一排非線性嚙合力作用后的結(jié)果,所以其頻譜中存在更高諧次嚙頻和外激勵(lì)頻率的調(diào)制頻率。
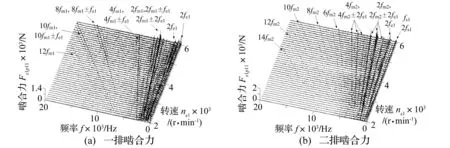
圖10 T 0=500N·m時(shí)單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖 Fig.10 The meshing force spectrum waterfall chart under the action of single frequency time-varying torque T 0=500N·m
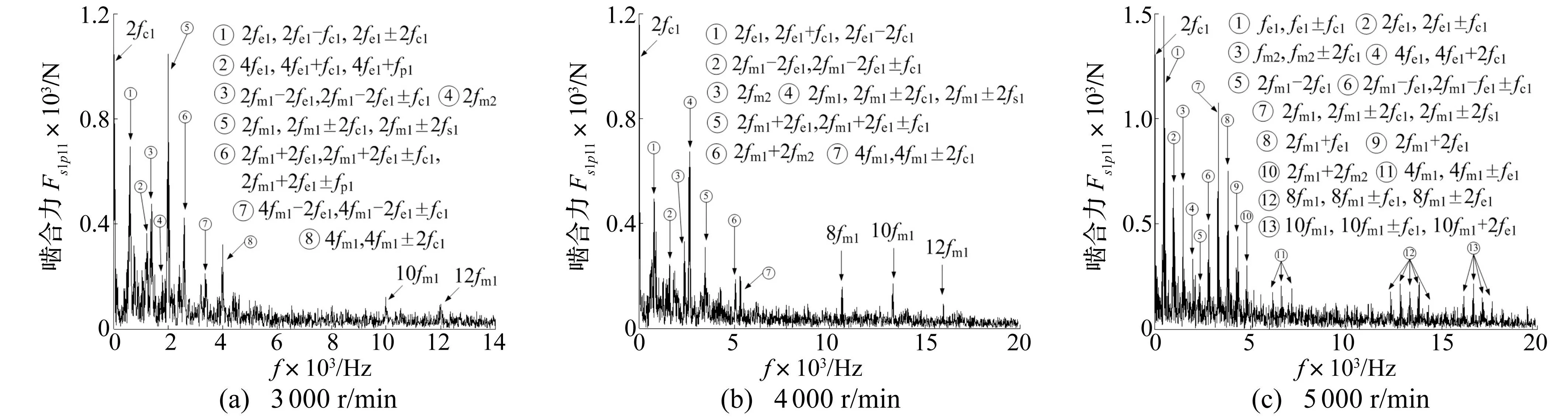
圖11 T 0=500N·m的時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的一排嚙合力頻譜圖 Fig.11 The meshing force spectrum of the first planetary under the action of time-varying torque T 0=500N·m and different rotating speed
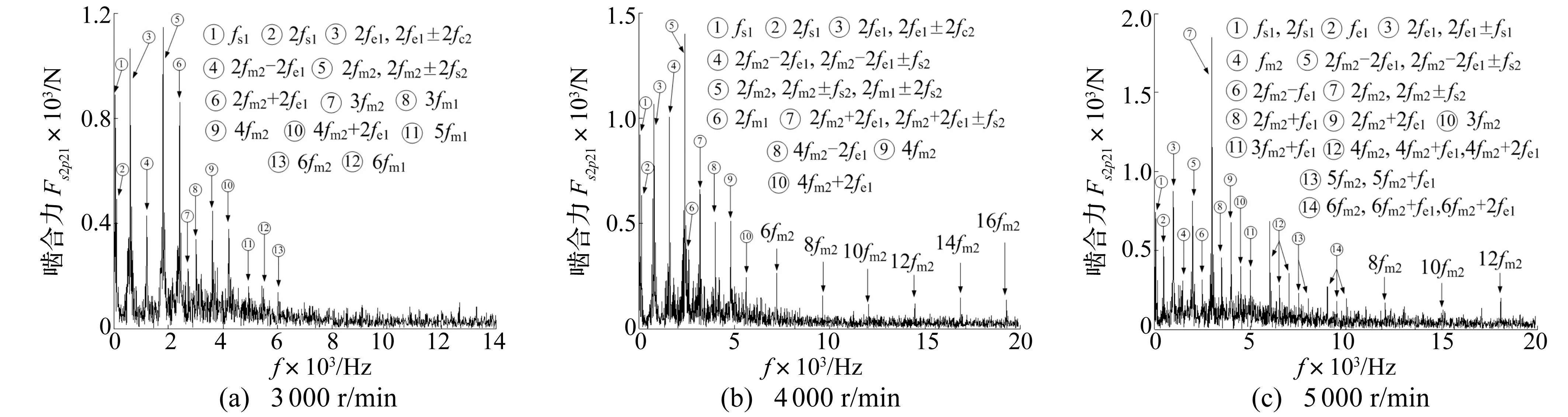
圖12 T 0=500N·m的時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的二排嚙合力頻譜圖 Fig.12 The meshing force spectrum of the second planetary under the action of time-varying torque T 0=500N·m and different rotating speed
T0=2000N·m的單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖見圖13。與T0=500N·m時(shí)的區(qū)別是在一排、二排嚙合力頻譜中不僅明確地出現(xiàn)耦合嚙頻、不同嚙頻的組合頻率,還有耦合嚙頻與外激勵(lì)頻率的調(diào)制頻率。這說明時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩平均值增大時(shí),嚙合力頻譜出現(xiàn)了新的耦合形式,不僅不同行星排嚙頻的耦合作用增強(qiáng),而且各嚙頻與外激勵(lì)頻率的調(diào)制作用也增強(qiáng)。
部分轉(zhuǎn)速下的嚙合力頻譜見圖14和圖15。在一排嚙合力頻譜中出現(xiàn)了2(fm1+fm2)形式的組合頻率,2fm2±2fe1、2fm2±2fc1形式的調(diào)制頻率。在二排嚙合力頻譜中,耦合頻率形式則以μfm1,μ=2,3,4,為主要。這說明嚙頻耦合作用對(duì)一排嚙合力的影響大于對(duì)二排嚙合力。
通過以上在定值驅(qū)動(dòng)轉(zhuǎn)矩、時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩不同工況下的嚙合力頻譜分析可以看出,耦合后嚙合力除了本級(jí)行星排各部件的轉(zhuǎn)頻與嚙頻之外,還出現(xiàn)四種新頻率:非本級(jí)行星排嚙頻、兩個(gè)行星排嚙頻的組合頻率、非本級(jí)行星排嚙頻與本級(jí)行星排部件轉(zhuǎn)頻的調(diào)制頻率、非本級(jí)行星排嚙頻與外激勵(lì)頻率的調(diào)制頻率。
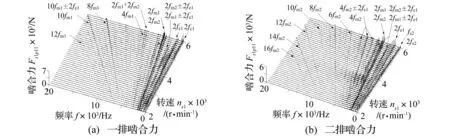
圖13 T 0=2000N·m時(shí)單頻時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力頻譜瀑布圖 Fig.13 The meshing force spectrum waterfall chart under the action of single frequency time-varying torque T 0=2000N·m
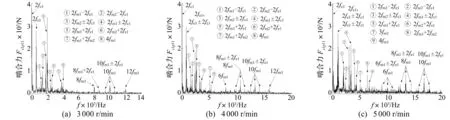
圖14 T 0=2000N·m的時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的一排嚙合力頻譜圖 Fig.14 The meshing force spectrum of the first planetary under the action of time-varying torque T 0=2000N·m and different rotating speed

圖15 T 0=2000N·m的時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩下不同轉(zhuǎn)速的二排嚙合力頻譜圖 Fig.15 The meshing force spectrum of the second planetary under the action of time-varying torque T 0=2000N·m and different rotating speed
2.4動(dòng)載特性與均載特性
在多級(jí)行星齒輪傳動(dòng)中,不僅嚙合狀態(tài)不同會(huì)造成同一級(jí)行星排的多個(gè)外、內(nèi)嚙合力之間存在差異,而且各連接軸質(zhì)量、剛度特性的不同也會(huì)形成每一級(jí)行星排嚙合力不同的動(dòng)態(tài)特性。本文采用動(dòng)載系數(shù)和均載系數(shù)評(píng)價(jià)嚙合力的動(dòng)態(tài)特性。
外嚙合力動(dòng)載系數(shù)Gsipij定義為
(20)
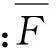
不同行星排連接軸的動(dòng)載系數(shù)Thiql定義為
(21)
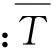
外嚙合力的均載系數(shù)Bsipij定義為
(22)
內(nèi)嚙合力的均載系數(shù)與外嚙合力的定義類似。
本文將一排嚙合力Fs1p11、二排嚙合力Fs2p21、一排太陽輪與二排太陽輪連接軸扭矩Ts1s2、一排行星架與二排齒圈連接軸扭矩Tc1r2的動(dòng)態(tài)特性進(jìn)行對(duì)比分析。不同定值驅(qū)動(dòng)轉(zhuǎn)矩下各嚙合力、轉(zhuǎn)矩的動(dòng)載系數(shù)見圖16和圖17,可以看出,動(dòng)載系數(shù)從大到小依次是:一排嚙合力,二排嚙合力,一排行星架與二排齒圈連接軸,
一排太陽輪與二排太陽輪連接軸。在兩個(gè)行星排中,內(nèi)嚙合動(dòng)載系數(shù)大于外嚙合。從整體看,在T0=500N·m時(shí)的系統(tǒng)動(dòng)載系數(shù)大于T0=2000N·m時(shí)。在T0=500N·m時(shí),各嚙合力在ns1=3000r/min出現(xiàn)共振,從ns1=4000r/min開始隨轉(zhuǎn)速升高有增大趨勢(shì);而連接軸轉(zhuǎn)矩在ns1=3700r/min時(shí)出現(xiàn)共振。在T0=2000N·m時(shí),各嚙合力和扭矩同時(shí)發(fā)生共振,共振轉(zhuǎn)速為ns1=3800r/min,共振最明顯的是一排行星架與二排齒圈連接軸的扭轉(zhuǎn)轉(zhuǎn)矩。
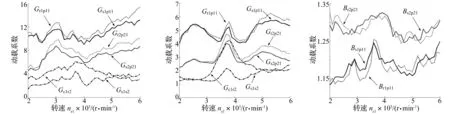

圖16 T0=500N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下系統(tǒng)動(dòng)載系數(shù)Fig.16ThedynamicloadcoefficientundertheactionofconstanttorqueT0=500N·m圖17 T0=2000N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下系統(tǒng)動(dòng)載系數(shù)Fig.17ThedynamicloadcoefficientundertheactionofconstanttorqueT0=2000N·m圖18 T0=500N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力均載系數(shù)Fig.18ThemeshingforceaverageloadcoefficientundertheactionofconstanttorqueT0=500N·m
不同定值驅(qū)動(dòng)轉(zhuǎn)矩下嚙合力均載系數(shù)見圖18和圖19,可以看出,二排嚙合力均載系數(shù)大于一排嚙合力。各行星排的內(nèi)、外嚙合力均載系數(shù)變換趨勢(shì)基本一致。在T0=2000N·m時(shí)的系統(tǒng)均載系數(shù)小于T0=500N·m時(shí)的均載系數(shù)。驅(qū)動(dòng)轉(zhuǎn)矩平均值增大有利于改善行星輪載荷分配情況。在T0=500N·m時(shí),一排嚙合力均載系數(shù)在ns1為2900r/min和3700r/min時(shí)出現(xiàn)峰值。在T0=2000N·m時(shí),一、二排嚙合力均載系數(shù)在ns1為3500r/min和4000r/min時(shí)出現(xiàn)峰值。
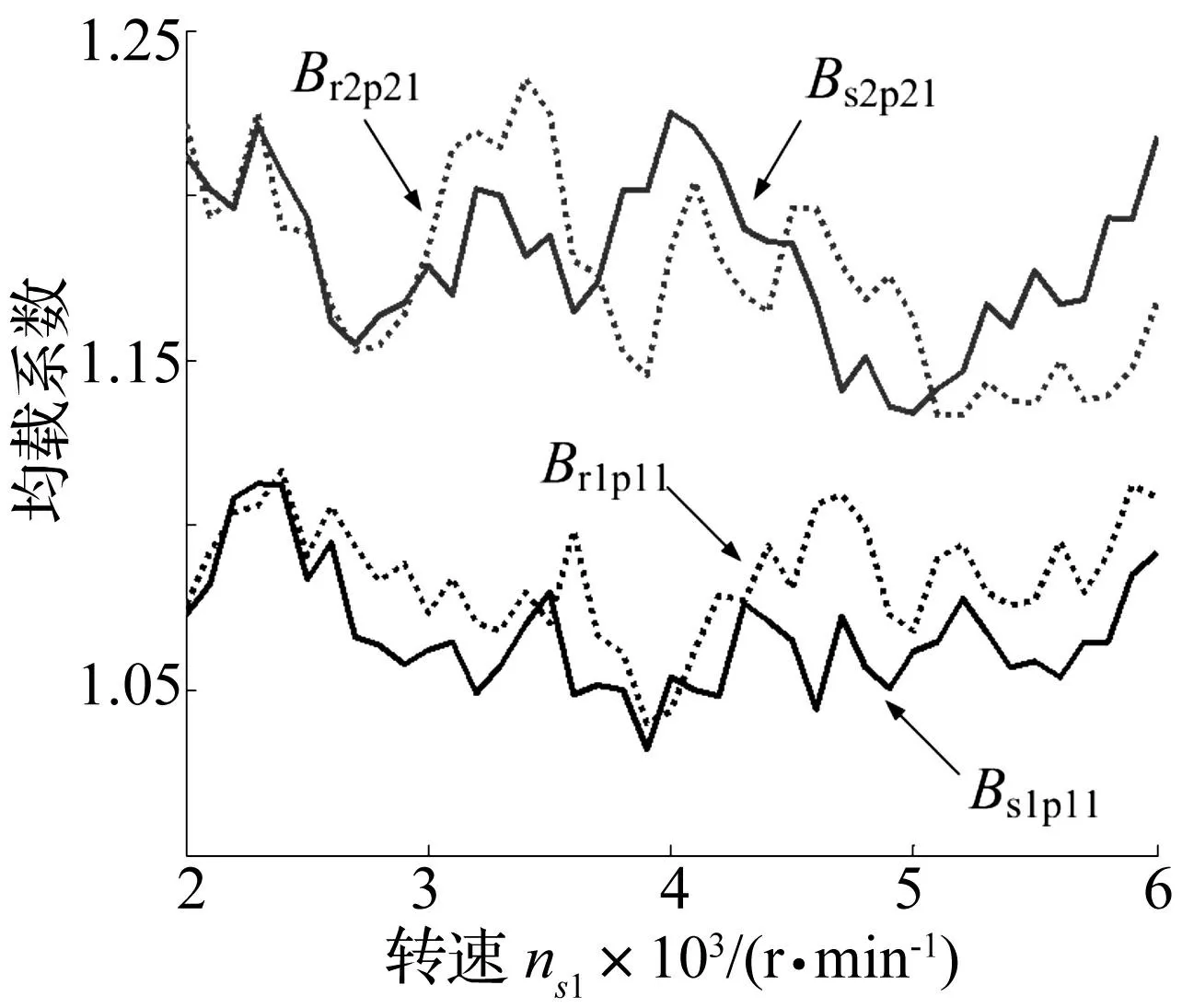
圖19 T 0=2000N·m的定值驅(qū)動(dòng)轉(zhuǎn)矩下 嚙合力均載系數(shù) Fig.19 The meshing force average load coefficient under the action of constant torque T 0=2000N·m
3結(jié)論
本文考慮齒側(cè)間隙、時(shí)變嚙合剛度及其相位差、制造誤差、安裝誤差、行星輪位置角時(shí)變性以及各行星排級(jí)間連接件的彎曲和扭轉(zhuǎn)剛度,在統(tǒng)一的固定參考系中建立了兩級(jí)行星齒輪傳動(dòng)的平移-扭轉(zhuǎn)非線性振動(dòng)模型。
以一排太陽輪與二排太陽輪連接軸為例,從連接軸內(nèi)力與變形耦合關(guān)系出發(fā),闡述了兩個(gè)行星排嚙合力產(chǎn)生嚙合頻率耦合的過程。解釋了不同行星排嚙頻及其相關(guān)頻率同時(shí)出現(xiàn)在嚙合力頻譜中的雙嚙頻耦合振動(dòng)現(xiàn)象。
通過數(shù)值方法計(jì)算了兩級(jí)行星排在不同形式驅(qū)動(dòng)轉(zhuǎn)矩作用下的動(dòng)態(tài)嚙合力。從頻譜分析看出,嚙合頻率耦合的表現(xiàn)形式與外激勵(lì)條件有密切關(guān)系。時(shí)變驅(qū)動(dòng)轉(zhuǎn)矩作用時(shí)的耦合頻率表現(xiàn)形式比定值驅(qū)動(dòng)轉(zhuǎn)矩時(shí)的更加復(fù)雜。轉(zhuǎn)速升高、平均載荷增大都會(huì)引起頻率耦合作用增強(qiáng)。耦合后的嚙合力除了本級(jí)行星排各部件的轉(zhuǎn)頻與嚙頻之外,還出現(xiàn)了四種新頻率:非本級(jí)行星排嚙頻、兩個(gè)行星排嚙頻的組合頻率、非本級(jí)行星排嚙頻與本級(jí)行星排部件轉(zhuǎn)頻的調(diào)制頻率、非本級(jí)行星排嚙頻與外激勵(lì)頻率的調(diào)制頻率。同時(shí),嚙頻耦合產(chǎn)生的影響對(duì)各級(jí)行星排嚙合力頻譜并不是對(duì)等的,其對(duì)一排嚙合力的影響大于對(duì)二排。
對(duì)各行星排嚙合力、連接軸轉(zhuǎn)矩的動(dòng)態(tài)特性進(jìn)行了分析。動(dòng)載系數(shù)從大到小依次是:一排嚙合力,二排嚙合力,一排行星架與二排齒圈連接軸,一排太陽輪與二排太陽輪連接軸。而二排嚙合力均載系數(shù)大于一排嚙合力均載系數(shù)。
參考文獻(xiàn)
[1]Kahraman A. A kinematics and power flow analysis methodology for automatic transmission planetary gear trains [J]. Journal of Mechanical Design, 2004, 126(6): 1071-1081.
[2]Deur J, Asgari J, Hrovat D, et al. Modeling and analysis of automatic transmission engagement dynamics-linear case [J]. Journal of Dynamic Systems, Measurement, and Control, 2006, 128: 263- 277.
[3]Kiracofe D R, Parker R G. Structured vibration modes of general compound planetary gear systems [J]. Journal of Vibration and Acoustics, 2007, 129:1-16.
[4]Kahraman A. Free torsional vibration characteristics of compound planetary gear sets[J]. Mechanism and Machine Theory, 2001, 36(6): 953-971.
[5]Guo Yi-chao, Parker R G. Purely rotational model and vibration modes of compound planetary gears[J]. Mechanism and Machine Theory, 2010, 45: 365-377.
[6]Guo Yi-chao, Parker R G. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters[J]. Journal of Vibration and Acoustics 2010, 132(1)011006.
[7]李瑰賢,趙永強(qiáng),常山,等. 船用兩級(jí)雙排斜齒行星齒輪系統(tǒng)動(dòng)力學(xué)方程的建立[J]. 船舶力學(xué),2011,15(5):530-537.
LI Gui-xian, ZHAO Yong-qiang, CHANG Shan, et al. Study on dynamic governing equations of two stage double helical tooth planetary gear train used in ship[J]. Journal of Ship Mechanics, 2011, 15(5): 530-537.
[8]蔡仲昌,劉輝,項(xiàng)昌樂,等. 車輛行星傳動(dòng)系統(tǒng)扭轉(zhuǎn)振動(dòng)固有特性及靈敏度分析[J]. 中國(guó)機(jī)械工程,2011,22(1):96-101.
CAI Zhong-chang, LIU Hui, XIANG Chang-le, et al. Research on natural characteristics and sensitivity for torsional vibration of a vehicle multistage planetary gears[J]. China Mechanical Engineering, 2011, 22(1): 96-101.
[9]Inalpolat M, Kahraman A. Dynamic modelling of planetary gears of automatic transmissions[J]. Multi-body Dynamics, 2008, 138(222): 229-242.
[10]蔡仲昌,劉輝,項(xiàng)昌樂,等. 車輛多級(jí)行星傳動(dòng)系統(tǒng)強(qiáng)迫扭轉(zhuǎn)振動(dòng)與動(dòng)載特性[J]. 吉林大學(xué)學(xué)報(bào):工學(xué)版,2012,42(1):19-26.
CAI Zhong-chang, LIU Hui, XIANG Chang-le, et al. Characteristics of forced torsional vibration and dynamic load for vehicle multistage planetary transmission[J]. Journal of Jilin University:Engineering and Technology Edition, 2012, 42(1): 19-26.
[11]秦大同,肖正明,王建宏. 基于嚙合相位分析的盾構(gòu)機(jī)減速器多級(jí)行星齒輪傳動(dòng)動(dòng)力學(xué)特性[J]. 機(jī)械工程學(xué)報(bào),2011,47(23):20-29.
QIN Da-tong, XIAO Zheng-ming, WANG Jian-hong. Dynamic characteristics of multi-stage planetary gears of shield tunnelling machine based on planet mesh phasing analysis[J]. Journal of Mechanical Engineering, 2011, 47(23): 20-29.
[12]肖正明,秦大同,王建宏,等. 盾構(gòu)機(jī)主減速器三級(jí)行星傳動(dòng)系統(tǒng)扭轉(zhuǎn)動(dòng)力學(xué)[J]. 中國(guó)機(jī)械工程,2010,21(18):2176-2182.
XIAO Zheng-ming, QIN Da-tong, WANG Jian-hong,et al. Study on torsional dynamic of 3-stage planetary gears of main reducer used in driving cutterhead of shield tunnelling machine[J]. China Mechanical Engineering, 2012, 21(18): 2176-2182.
[13]Al-shyyab A, Alwidyan K, Jawarneh A. Non-linear dynamic behaviour of compound planetary gear trains: model formulation and semi-analytical solution[J]. Journal of Multi-body Dynamics, 2009, 223:199-210.
[14]朱自冰,朱如鵬,鮑和云. 兩級(jí)星型齒輪傳動(dòng)系統(tǒng)非線性動(dòng)力學(xué)研究[J]. 航空動(dòng)力學(xué)報(bào),2007,22(11): 1963-1970.
ZHU Zi-bing, ZHU Ru-peng, BAO He-yun. Non-linear dynamic study of 2-stage star gear train[J]. Journal of Aerospace Power, 2007,22(11): 1963-1970.
[15]孫智民,沈允文,李素有. 封閉行星齒輪傳動(dòng)系統(tǒng)的動(dòng)態(tài)特性研究[J]. 機(jī)械工程學(xué)報(bào),2002,38(2):44-48.
SUN Zhi-min, SHEN Yun-wen, LI Su-you. Study on dynamic behavior of encased differential gear train[J]. Chinese Journal of Mechanical Engineering, 2002, 38(2):44-48.
[16]劉輝, 蔡仲昌,朱麗君,等. 多工況條件下單級(jí)行星傳動(dòng)非線性振動(dòng)特性研究[J]. 兵工學(xué)報(bào),2012,33(10):1153-1161.
LIU Hui,CAI Zhong-chang, ZHU Li-Jun, et al. Study on nonlinear vibration behavior of simple single stage planetary gears in multiple work conditions[J]. Acta Armamentarii, 2012, 33(10): 1153-1161.
[17]劉輝,蔡仲昌,項(xiàng)昌樂.發(fā)動(dòng)機(jī)激勵(lì)下行星傳動(dòng)非線性嚙合力的動(dòng)態(tài)特性研究[J]. 振動(dòng)、測(cè)試與診斷,2014, 34(1):83-89.
LIU Hui, CAI Zhong-chang, XIANG Chang-le. Study on nonlinear meshing force dynamic behavior of planetary gears on engine excitation[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(1): 83-89.
[18]Parker R G, Lin J. Mesh phasing relationships in planetary and epicyclic gears[J]. Journal of Mechanical Design, 2004, 126: 365 -370.

第一作者陳玉震男,博士,1987年生
通信作者陳飆松男,博士,教授,1973年生

