非均質結構非平穩隨機響應的快速算法

非均質結構非平穩隨機響應的快速算法

陳玉震, 張盛, 陳飆松, 張洪武

(大連理工大學工業裝備結構分析國家重點實驗室運載工程與力學學部工程力學系,遼寧大連116024)

摘要：將擴展多尺度有限元法應用于非平穩隨機振動時域顯式法中，實現了對非均質結構非平穩隨機響應的快速精確計算。首先，論文闡述了擴展多尺度有限元法基本原理。其次，探討了時域顯式法在非平穩隨機響應分析中的優勢。時域顯式法基于動力響應顯式表達式直接在時域進行隨機振動分析，較傳統反應譜法，具有良好的計算精度和計算效率。最后，根據兩算法的特性和優勢提出統一的多尺度算法框架，使其適用于非均質結構非平穩隨機響應分析的快速求解。數值算例驗證了該算法的高效性和精確性。

關鍵詞：非均質結構; 非平穩隨機振動； 擴展多尺度有限元法; 基函數； 時域顯式法

中圖分類號:TB122

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.19.004

Abstract:A fast computation was implemented for non-stationary random responses of heterogeneous material structures by applying the extended multiscale finite element method (EMsFEM) into the time-domain explicit method(TDEM). Firstly, the fundamental principle of EMsFEM was presented. Then, the advantages of TDEM in non-stationary random response analysis were explored. Based on the explicit expressions of dynamic responses, the random response analysis was performed directly in time domain, it was shown that TDEM has good accuracy and efficiency compared with the response spectrum method. Finally, according to the characteristics and advantages of the two algorithms, a unified multiscale framework was proposed, it was applicable for non-stationary random response analysis of heterogeneous material structures. Numerical examples showed that the proposed method has high efficiency and accuracy.

基金項目：國家自然科學基金資助項目(51275540)；中央高校基本科研業務費資助項目(CDJZR13110001)

收稿日期：2014-08-07修改稿收到日期：2014-10-17

A fast algorithm for non-stationary random responses of heterogeneous material structures

CHENYu-zhen,ZHANGSheng,CHENBiao-song,ZHANGHong-wu(State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, China)

Key words:heterogeneous material structures; non-stationary random response; extended multiscale finite element method (EMsFEM); base function; time-domain explicit method (TDEM)

自然存在以及人工形成的大部分材料都具有非均質特性，例如地下巖土以及航空航天工業中廣泛使用的復合材料等，由這些非均質材料構成的結構，在工程實踐中每時每刻都要受到各種形式的動態載荷，其中，非平穩隨機激勵是最為普遍的一種載荷形式，例如地震作用、陣風載荷等，為了確保這些結構的可靠性與安全性，研究非均質結構在非平穩隨機激勵作用下的動力響應具有非常重要的意義。

在隨機振動分析中，功率譜法是求解隨機響應的主要方法[1-2]，對于多點(m點)非平穩隨機響應問題，為了求解各離散頻點處的響應功率譜，功率譜法在每個頻點都需要進行約m次時程分析，對于大規模結構，計算量巨大，工程中難以接受。時域顯式法[3-4](TDEM)從時域出發，根據線性動力系統輸入與輸出之間的線性關系，建立各時刻結構響應關于隨機激勵的顯式表達式，從而可以直接利用一階矩和二階矩的運算規律計算各時刻結構響應的均值和方差，對于在m個非平穩隨機激勵作用下的結構，顯式表達式的建立只需要進行2m次時程分析，計算量小，工程中容易接受。時域顯式法中結構響應已經完全解耦，只需要對所關心的響應求解即可，實現了空間尺度降維。當隨機響應的均值和方差為時間的慢變函數時，時域顯式法可以在較大時間間隔上計算響應的均值和方差，實現了時間尺度降維。時域顯式法僅需要非平穩隨機激勵時域相關函數信息，所以可以摒棄各種功率譜模型，適用范圍更廣。時域顯式法是一種高效、精確的非平穩隨機振動分析方法。

時域顯式法在求解非均質結構的非平穩隨機響應時，為了捕獲結構的微觀非均質特性，結構網格需要剖分的非常細致，這使得結構規模巨大，甚至無法計算。多尺度方法[5]是求解非均質結構力學性能的一種有效途徑，本文選用擴展多尺度有限元法[6](EMsFEM)，且為了能夠求解結構動力響應，與傳統擴展多尺度有限元法不同，該方法[7]是以各時間步內等效靜力平衡方程為基礎，數值構造出滿足局部特性微分算子并能反映結構動力性能的多尺度基函數，從而在宏觀尺度上對原問題進行求解，很大程度地減少計算量。時域顯式法的主要計算來自2m次時程分析，將擴展多尺度有限元法引入時域顯式法中，能夠很大程度的減少每次時程分析的計算量，從而使得原問題能夠快速求解。數值算例表明，擴展多尺度有限法與時域顯式法的結合應用，在保證精度的同時大大提高了計算效率，為非均質結構的非平穩隨機響應分析提供了一種快速精確的計算方法。

1擴展多尺度有限元法

擴展多尺度有限元法的基本思想是通過局部求解宏觀單元域內的平衡方程，數值構造出宏觀單元的多尺度基函數(形函數)，這些基函數能反映宏觀單元內部的微觀非均質特征，從而只需在宏觀尺度上對原問題進行求解即可以獲得滿意的結果，大大減少了計算量。擴展多尺度有限元法的計算流程主要可分為三個部分[8-9]，即多尺度基函數構造、宏觀計算、降尺度計算，本節以二維問題為例簡要介紹一下這一流程。

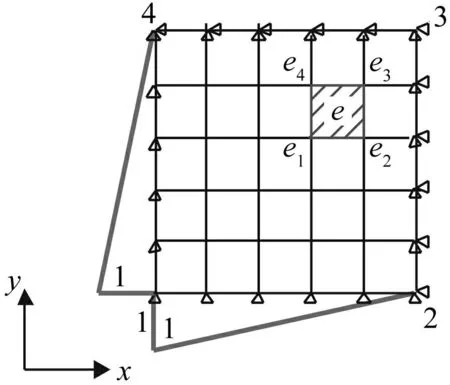
圖1　四節點宏觀單元 Fig.1 Four-node coarse element

1.1多尺度基函數構造

見圖1的某平面四節點宏觀單元，其內部微觀節點的位移可以表示為

(1)

式中:N為宏觀單元的多尺度基函數矩陣；u單胞內所有微觀節點的位移向量；u′E為宏觀單元四個節點的位移向量。它們可以表達成如下公式

u=[u1v1u2v2…unvn]T

N=[RT1RT2…RTn]T

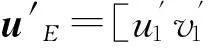
(2)

其中

(3)

式中,n為子網格的微觀節點總數，Nixy表示在宏觀節點i發生x方向單位位移時，宏觀單元的子網格上所有微觀節點產生的y向位移值。

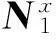
1.2宏觀計算

當多尺度基函數構造完成后，即可推導得到相應宏觀單元的等效剛度陣。見圖1，考慮子網格內任意一個細網格單元e，其節點編號為(e1，e2，e3，e4)，單元e的彈性應變能Πe可表達為

(4)

式中:Ke是單元e的常規剛度矩陣；ue是單元e的節點位移向量。

由式(1)和式(2)可得細網格單元e的節點位移向量與相應的宏觀單元節點位移向量的關系為

ue=Geu′E,Ge=[RTe1RTe2RTe3RTe4]T

(5)

式中:Ge為細網格單元e的轉換矩陣，其表征細網格單元e和對應的宏觀單元之間的節點位移映射關系。

將宏觀單元內部的所有細網格單元應變能力相加，可得到該宏觀單元的等效剛度陣

(6)

式中:p為宏觀單元內部細網格單元的總數。

宏觀單元的等效剛度陣獲取后，就可以組裝總體剛度陣，建立宏觀層次的求解方程，進而進行宏觀尺度的求解。

1.3降尺度計算

宏觀計算后，即可利用式(1)得到宏觀單元內部任一細網格單元e的節點位移ue，進而可以得到該單元的應力應變

εe=Beue=Teu′E,Te=BeGe

(7)

和

σe=Deεe=Seu′E,Se=DeBeGe

(8)

依次在各宏觀單元內計算，即可得到整個結構的微觀位移Yk+1、微觀應力σk+1和微觀應變εk+1。

2非平穩隨機振動時域顯式法

2.1動力響應顯式表達式

對于n個自由度的線性體系，在m個激勵作用下結構體系的運動方程可寫為

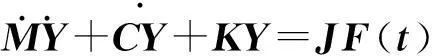
(9)

文獻[3-4]從精細積分法出發推導動力響應顯式表達式，本文從更一般的時程積分法Newmark法出發推導動力響應顯式表達式。記時間步長為Δt，時間步數為l，外載F(t)在時刻t0,t1,…,tl處的值分別記做F0,F1,…,Fl。結構第k+1步的響應可由第k步的響應遞推得到，遞推公式為

Vk+1=TVk+WFk+1

(10)

式中,

(11)

其中

(12)

(13)

(15)

記做

V0=QF0

(16)

則由遞推公式可寫出時刻ti=iΔt時刻，結構動力響應Vi的表達式

Vi=Ai,0F0+Ai,1F1+…+Ai,iFi

(i=1,2,…,l)

(17)

式中,Ai,0,Ai,1,…Ai,i的值為

(18)

各時刻響應遞推公式展開后形式如下

V1=A1,0F0+A1,1F1

V2=A2,0F0+A2,1F1+A2,2F2

?

Vl=Al,0F0+Al,1F1+…+

Al,l-1Fl-1+Al,lFl

(19)

矩陣形式為

V=AR

(20)

式中:V=[VT1VT2…VTl]T，R=[FT0FT1…FTl]T。

第i時刻的響應，可進一步表示為

Vi=AiRi,(i=1,2,…,l)

(21)

其中

(22)

式(17)或式(21)即為結構動力響應顯式表達式。

2.2響應均值和方差

結構動力響應顯式表達式只與結構相關，與外載性質無關，當外載F(t)為隨機激勵時，動力響應顯式表達式依然成立。此時，隨機激勵F(t)在各時刻的離散量F0,F0,…,Fl，分別為一隨機激勵。根據一階矩與二階矩的運算規律，由式(21)可得時刻ti處響應Vi的均值向量和協方差矩陣分別為

E[Vi]=AiE[Ri](i=1,2,…,l)

(23)

cov[Vi,Vi]=Aicov[Ri,Ri]ATi

(i=1,2,…,l)

(24)

式中,E[Ri]和cov[Ri,Ri]分別為隨機激勵向量的均值向量和協方差矩陣，可分別由F(t)的均值函數向量和互相關函數矩陣求出。

式(21)中，結構響應已完全解耦，可只計算所關心的響應量，即

vi=aiRi(i=1,2,…,l)

(25)

在結構隨機振動分析中，一般只對結構某些關鍵部位的響應感興趣，并不需要求解所有響應的均值和方差。由式(25)即可實現對關鍵部位響應均值和方差的單獨計算，如下式

μvi=E(vi)=aiE(Ri)(i=1,2,…,l)

(26)

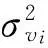
(i=1,2,…,l)

(27)

這樣實現了對結構的空間尺度降維，大大節省了計算量，提高了計算效率。

為了滿足積分精度和激勵描述的需要，時間步長為Δt不能太大，因此動力響應顯式表達式的推導是在一系列間隔較小的離散時間點上進行的。但當隨機響應的均值和方差為時間t的慢變函數時，并不需要在上述每一個時刻計算響應的均值和方差，即可在較大時間間隔上應用式(26)和(27)，這樣實現了對結構的時間尺度降維，進一步提高了計算效率。

由上述過程可以看出，時域顯式法求解響應均值和方差時，直接采用隨機激勵的時域相關函數信息，無需用到在時頻域中表征隨機激勵的時變功率譜密度函數信息，可以摒棄非平穩隨機激勵的各種功率譜模型，適用范圍更廣。

2.3時域顯式法系數矩陣的快速計算

時域顯式法在隨機響應分析時主要包含兩部分計算：一是動力響應顯式表達式中系數矩陣的計算；二是基于動力響應顯式表達式的隨機響應計算。當只求解結構某些關鍵部位的響應時，時域顯式法的計算量主要來自前者。而由式(18)可以發現，整個系數矩陣除第一列Ai,0與第二列Ai,1(i=1,2,…,l)需要單獨計算外，其他各列均可由前兩列遞推得到。

當結構受單點激勵作用(例如隨機地震作用)時，Ai,0和Ai,1為3n維向量。由式(17)及式(19)可知，Ai,0的值為在t=0時刻施加單位脈沖載荷F0=1，其他時刻載荷為0時，結構在各時刻的響應Vi。而Ai,1的值為在t=Δt時刻施加單位脈沖載荷F1=1，其他時刻載荷為0時，結構在各時刻的響應Vi。此時，僅需要2次時程分析即可得到系數矩陣前兩列，進而遞推得到整個系數矩陣。

當結構受m(m≥2)點激勵作用時，Ai,0和Ai,1為3n×m維矩陣。此時Ai,0每列的值分別為t=0時刻在各激勵點源依次施加單位脈沖載荷F0,j=1(j表示第j個激勵點源，j=1,2,…,m)，其他時刻載荷為0時，結構在各時刻的響應Vi,j。而Ai,1每列的值分別為t=Δt時刻在各激勵點源依次施加單位脈沖載荷F1,j=1(j=1,2,…,m)，其他時刻載荷為0時，結構在各時刻的響應Vi,j。此時，僅需要2m次時程分析即可得到系數矩陣前兩列，進而遞推得到整個系數矩陣。

3時域顯式法的多尺度框架

由第2節內容可知，采用時域顯式法計算非平穩隨機振動的主要計算量來自2m次特定脈沖激勵下的時程分析，提高單次時程分析的計算效率成為提高整個算法效率的關鍵。對于非均質結構，采用多尺度方法是減小問題規模，提高計算效率的有效途徑，為了能夠求解非均質結構的動力響應，本文所采用的擴展多尺度方法以各時間步內等效靜力平衡方程為基礎來構造多尺度基函數，其余過程與第1節相同。為了提高計算精度，本文采用多節點宏觀單元策略[10]。本節將詳細介紹一下將多尺度方法引入時域顯式法，構建時域顯式法多尺度框架的基本流程。框架圖見圖2，基本流程如下:

(1)讀取粗細網格信息，基于各時間步等效靜力平衡方程計算各宏觀單元動力基函數Nd。

(4)構造2m個脈沖激勵，1:m個激勵在t=0時刻施加，m+1:2m個激勵在t=Δt時刻施加，其幅值均為：F=JE，J為一n×m階常數矩陣，用于定位激勵，E為m×m階單位矩陣。

(5)初始狀態計算，根據構造激勵計算宏觀初始狀態向量，并降尺度得到微觀初始狀態向量。

(6)各時間步內等效載荷為

(28)

此時，載荷直接施加在微觀網格上，這將產生不平衡節點力，本文采用位移分解技術[10]來處理，真實位移u被分解成宏觀整體響應u′和局部擾動響應u″，u′由宏觀等效力驅動，u″則由微觀擾動力驅動，本步驟即計算第k步宏觀整體等效載荷及各單胞域內微觀等效載荷。

(9)判斷是否達到最大時間步，完成整個時程分析計算。

(10)提取2m個時程響應結果，組裝得到系數矩陣前兩列Ai,0與Ai,1(i=1,2,…,l)。

(11)由系數矩陣前兩列，遞推得到整個系數矩陣A。

(12)通過式(26)或(27)計算響應均值和方差。

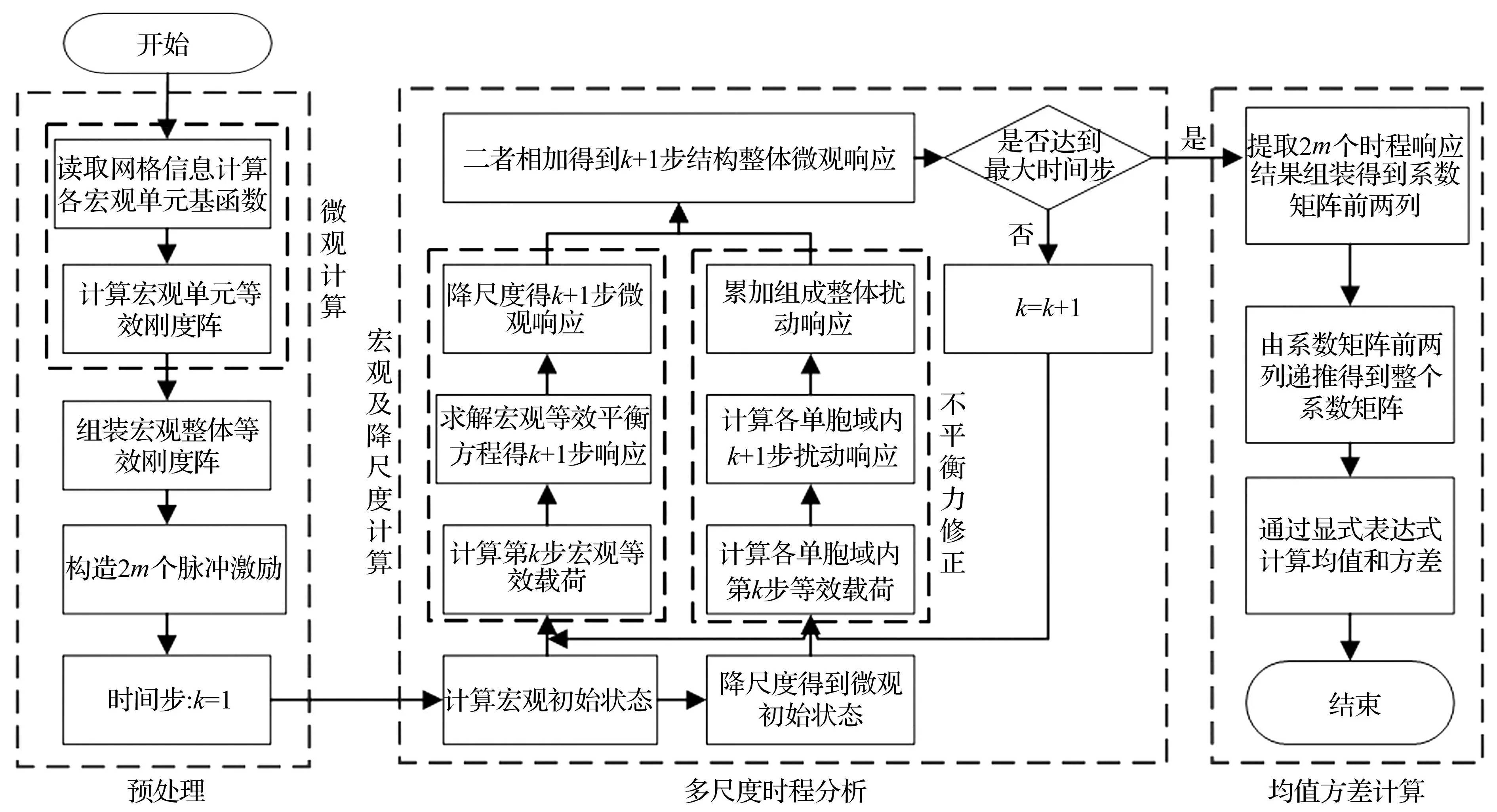
圖2　時域顯式法多尺度框架 Fig.2 The multiscale framework for TDEM

4數值算例

通過2個數值算例來驗證本文算法的有效性。為了便于比較，兩算例均以虛擬激勵法的計算結果作為參考解。

兩算例均采用下列形式的均勻調制非平穩激勵

F(t)=g(t)f(t)

(29)

式中,g(t)為均勻調制函數，有兩種形式

g1(t)=1

(30)

(31)

f(t)的自譜密度均取過濾白噪聲模型

(32)

式中,tb=8.5s,tc=20.0s,c1=0.1572,S0=142.75,ωg=19.07,ζg=0.544。

兩算例中，結構尺寸及材料屬性等數據均為無量綱量。計算所取時間和頻率分別為t∈[0,40],Δt=0.5和ω∈[0,50],Δω=0.5。均采用瑞利阻尼，系數為α=0.015和β=0.02。

4.1算例1周期性非均質結構受非平穩水平地面加速度響應分析

見圖3(a)T型結構，無量綱尺寸圖中已給出，細網格單元尺寸為10×10，粗網格單元尺寸為100×100，粗網格剖分及單胞見圖3(b)。結構底部全約束，整體受一非平穩水平地面加速度作用，均勻調制函數由式(31)給定，激勵自譜密度由式(32)給定。結構由5種無量綱材料周期性構成，各材料屬性見表1，計算右上頂點處的位移均方值。

圖3　T型結構模型圖 Fig.3 The T-shape structure model

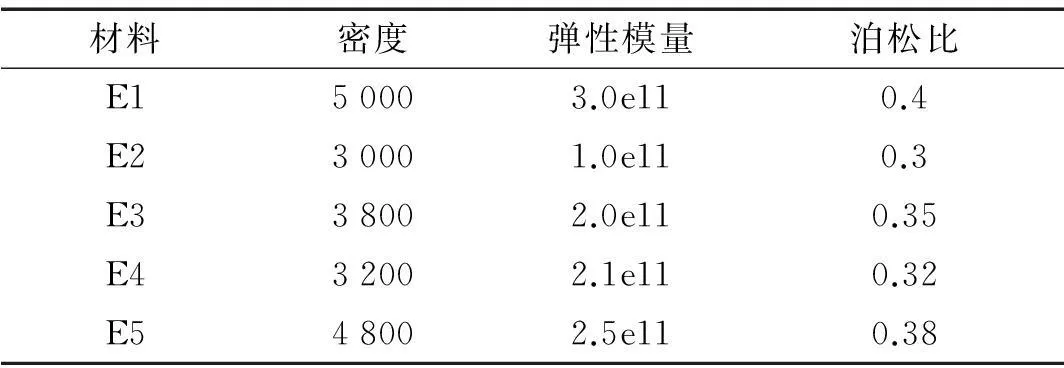
材料密度彈性模量泊松比E150003.0e110.4E230001.0e110.3E338002.0e110.35E432002.1e110.32E548002.5e110.38

粗網格單元邊界宏觀節點數依次取2、4、6和8，四種情況下虛擬激勵法(PEM)、時域顯式法(TDEM)以及擴展多尺度時域顯式法(EMsTDEMm)的計算結果見圖4，其中m表示粗網格單元邊界宏觀節點數目。以虛擬激勵法(PEM)作為數值參考解，其他方法相對數值誤差通過L2范數定義，其公式如下：

(33)

式中,va表示PEM參考解，v表示TDEM及EMsTDEMm計算結果；n為時間步數。

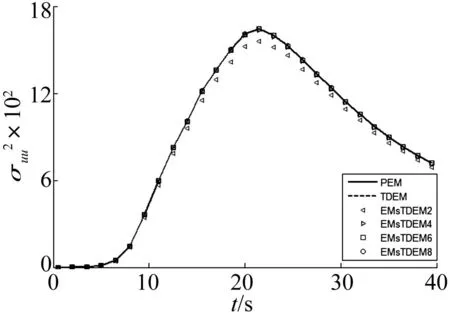
圖4　端點位移均方值 Fig.4 Mean square of the endpoint displacement

由圖4及表2中的L2范數可以看出，TDEM與PEM的計算精度一致。隨著邊界宏觀節點數目的增加，EMsTDEMm的計算精度逐漸趨近PEM，當m=8時，基本一致。

由表2中的計算時間可得，TDEM計算用時遠遠小于PEM。隨著邊界宏觀節點數目的增加，EMsTDEMm的計算用時逐漸增加，但效率較TDEM依然有極大的提高。

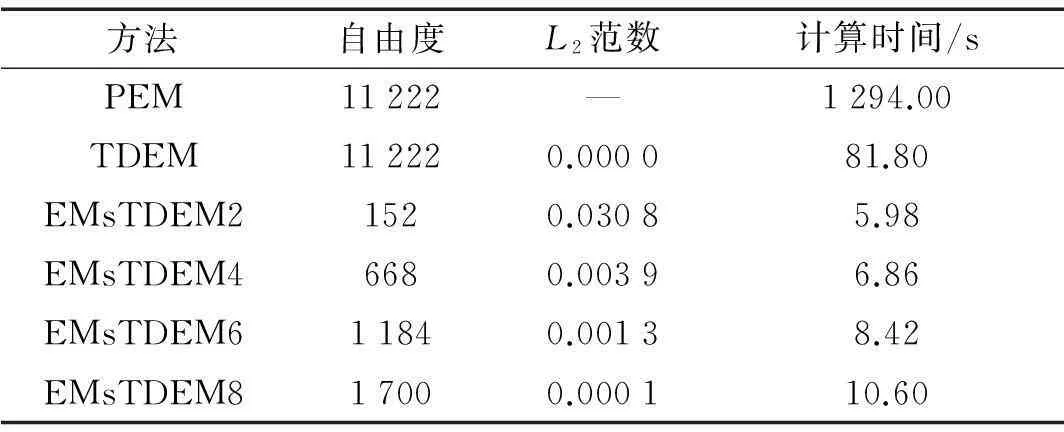
表2　L 2范數及計算用時

4.2算例2 隨機非均質懸臂梁結構受多點部分相干隨機激勵響應分析

見圖5(a)T型結構，無量綱尺寸圖中已給出，細網格單元尺寸為5×2.5，粗網格單元尺寸為50×25，粗網格剖分及單胞見圖5(b)。懸臂梁左端全約束，上邊界中點與右端點處施加兩部分相干隨機激勵。結構由3種材料構成(見表3)，且3種材料在結構中完全隨機分布，計算右下端點處的位移均方值。

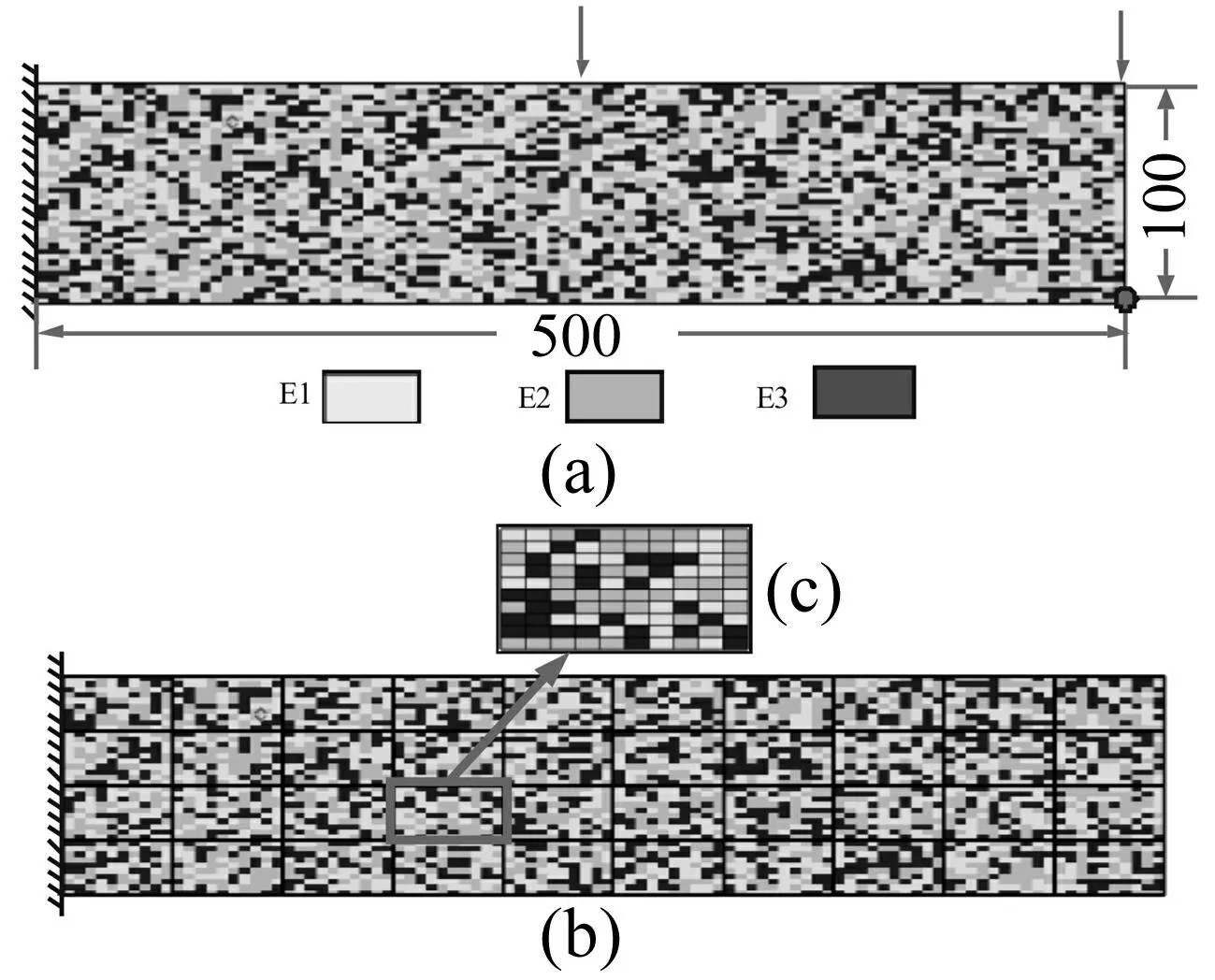
圖5　懸臂梁結構模型圖 Fig.5 The cantilever structure model

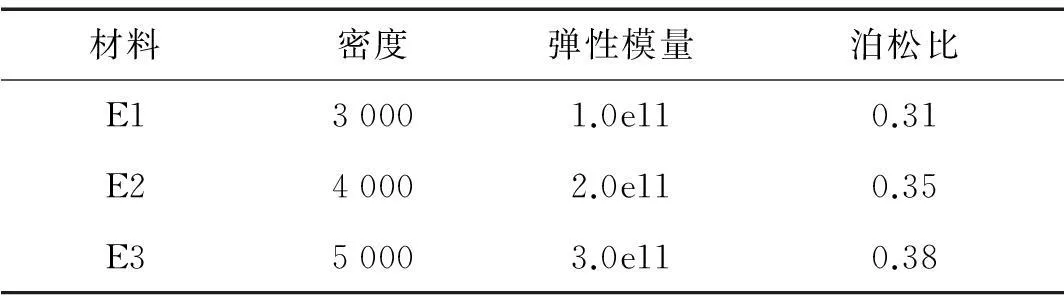
材料密度彈性模量泊松比E130001.0e110.31E240002.0e110.35E350003.0e110.38

兩隨機激勵的均勻調制函數分別由式(31)和(30)給定，激勵自譜密度分別取式(32)及S0，兩激勵相干矩陣為

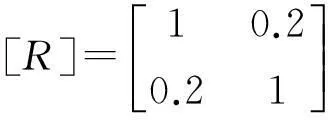
(34)

粗網格單元邊界宏觀節點數依次取2、5、8和11，四種情況下虛擬激勵法(PEM)、時域顯式法(TDEM)以及擴展多尺度時域顯式法(EMsTDEMm)的計算結果見圖6，其中m表示粗網格單元邊界宏觀節點數目，L2范數及計算用時見表4。

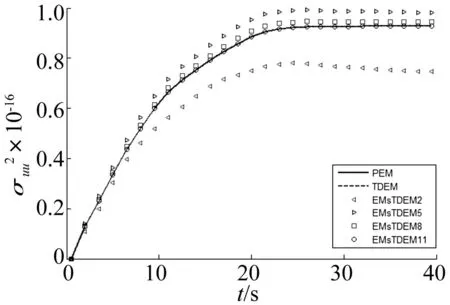
圖6　結構端點位移方差 Fig.6 The variance of the structure’s endpoint

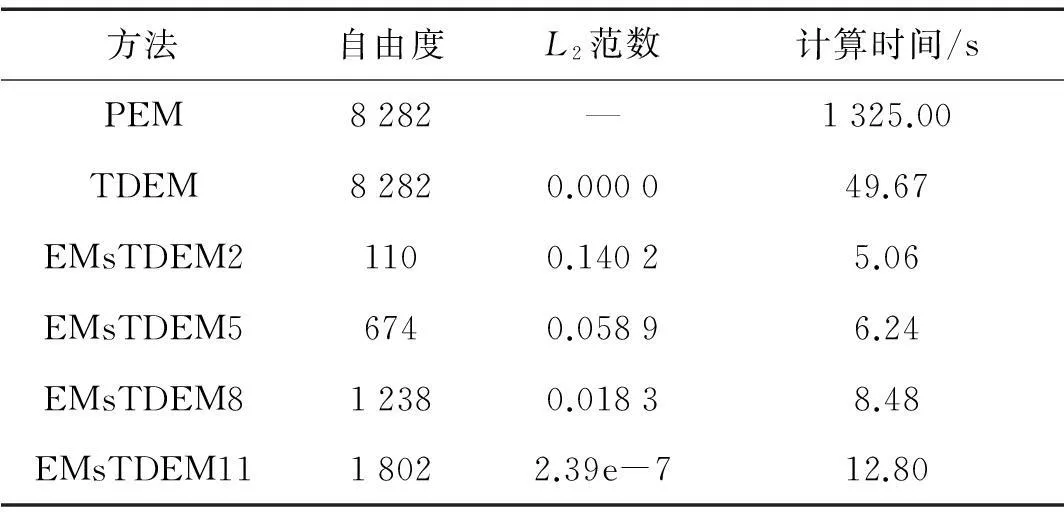
方法自由度L2范數計算時間/sPEM8282—1325.00TDEM82820.000049.67EMsTDEM21100.14025.06EMsTDEM56740.05896.24EMsTDEM812380.01838.48EMsTDEM1118022.39e-712.80

由圖6及表4中的L2范數可以看出，TDEM與PEM的計算精度一致。隨著邊界宏觀節點數目的增加，EMsTDEMm的計算精度逐漸趨近PEM，當m=11時，基本一致。

表4中的計算時間可得，TDEM計算用時遠遠小于PEM。隨著邊界宏觀節點數目的增加，EMsTDEMm的計算用時逐漸增加，但效率較TDEM依然有極大的提高。

此外，本文提出的擴展多尺度時域顯式法(EMsTDEMm)在計算單點、多點完全相干或者激勵點源不多的部分相干非平穩隨機振動時，具有顯著優勢，計算效率很高；但在處理激勵點源較多(m個)的部分相干非平穩隨機振動時，需要計算2m個脈沖激勵下結構的時程分析，計算量巨大，該方法會受到一定的限制，因此，需要進一步從并行程序設計角度來解決此問題。

5結論

大型復雜結構在非平穩隨機激勵作用下的響應分析仍是目前面臨的一個難點問題，當結構材料具有非均質特性時，分析變得更加困難。針對這一問題，本文從非平穩隨機響應分析算法和非均質結構動力響應算法兩個方面著手，提出一種適用于非均質結構平穩隨機響應分析的快速算法。非平穩隨機響應分析算法方面采用時域顯式法，該方法從時域出發建立結構動力響應顯式表達式，直接通過一階矩和二階矩計算結構響應的均值和方差。對于單點非平穩隨機響應分析，主要計算僅為2次時程分析，較功率譜法幾十至幾百次的時程分析，具有較高的計算效率。非均質結構動力響應算法方面，采用擴展多尺度有限元法，該法以時程分析各時間步的等效靜力平衡方程為基礎，構造能夠反映結構動力效應的廣義多尺度基函數，從而在宏觀尺度上對原動力問題進行求解，較常規有限元法，大大減小了問題規模，提高了計算效率。本文通過采用兩種方法相互耦合計算，為非均質復雜結構的非平穩隨機響應分析提供了一條可行途徑。數值算例表明，所提出算法在保證計算精度的前提下，具有很高的計算效率。

參考文獻

[1]Lin J H, Zhang W S, Li J J. Structural responses to arbitrarily coherent stationary random excitations[J]. Computers & structures, 1994, 50: 629-633.

[2]Lin J H, Li J J, Zhang W S, et al. Random seismic responses of multi-support structures in evolutionary inhomogeneous random fields[J]. Earthquake Engineering & Structural Dynamics, 1997, 26: 135-145.

[3]蘇成, 徐瑞. 非平穩激勵下結構隨機振動時域分析法[J]. 工程力學, 2010, 12:77-83.

SU Cheng, XU Rui. Random vibration analysis of structures subjected to non-stationary excitations by time domain method[J]. Engineering Mechanics, 2010,12:77-83.

[4]蘇成, 徐瑞, 劉小璐,等. 大跨度空間結構抗震分析的非平穩隨機振動時域顯式法[J]. 建筑結構學報, 2011, 11:169-176.

SU Cheng, XU Rui, LIU Xiao-lu,et al. Non-stationary seismic analysis of large-span spatial structures by time-domain explicit method[J]. Journal of Building Structures, 2011,11:169-176.

[5]Babuska I, Caloz G, Osborn E. Special finite element methods for a class of second order elliptic problems with rough coefficients[J]. SIAM J. Numer. Anal, 1994,31(4): 945-981.

[6]Zhang H W, Fu Z D, Wu J K. Coupling multiscale finite element method for consolidation analysis of heterogeneous saturated porous media[J]. Advances in Water Resources, 2009, 32(2): 268-279.

[7]Zhang H W, Lu M K, Zheng Y G, et al. General coupling extended multiscale FEM for elasto-plastic consolidation analysis of heterogeneous saturated porous media[J].International Journal for Numerical and Analytical Methods in Geomechanics,2015,39(1):63-95.

[8]張洪武, 吳敬凱, 劉輝,等. 擴展的多尺度有限元法基本原理[J]. 計算機輔助工程, 2010, 19(2): 3-9.

ZHANG Hong-wu, WU Jing-kai, LIU Hui, et al. Basic theory of extended multiscale finite element method[J]. Computer Aided Engineering, 2010, 19(2): 3-9.

[9]張洪武, 吳敬凱, 付振東. 周期性點陣桁架材料力學性能分析的一種新的多尺度計算方法[J]. 固體力學學報, 2011, 32(2): 109-118.

ZHANG Hong-wu, WU Jing-kai, FU Zhen-dong. A new multiscale computational method for mechanical analysis of periodic truss materials[J]. Chinese Journal of Solid Mechanics, 2011, 32(2): 109-118.

[10]Zhang S, Yang D S, Zhang H W, et al. Coupling extended multiscale finite element method for thermoelastic analysis of heterogeneous multiphase materials[J]. Computers and Structures, 2013, 121: 32-49.

第一作者楊洋女，碩士，1988年生

通信作者褚志剛男，博士，副教授，碩士生導師，1978年生