一種基于CR理論的大柔性機翼非線性氣動彈性求解方法

一種基于CR理論的大柔性機翼非線性氣動彈性求解方法

王偉1，周洲1，祝小平2，王睿1

(1.西北工業大學航空學院，西安710072；2. 西北工業大學無人機研究所，西安710065)

摘要：大展弦比大柔性機翼在氣動載荷的作用下，產生較大的彈性變形，其慣性特性、剛度特性、動氣動彈性特性等亦發生較大改變，常規的線性氣動彈性分析方法不再適用。基于Co-rotational(CR)理論，推導了機翼變形后的切線剛度矩陣和質量矩陣，建立了考慮幾何非線性效應的大柔性機翼結構動力學模型；耦合改進的ONERA非線性非定常氣動力模型，提出了一種適用于大柔性機翼的非線性氣動彈性求解方法。采用Newmark直接數值積分法及松耦合技術在時域內對氣動彈性運動方程進行求解，對所提出的非線性氣動彈性求解方法的正確性和精度進行了驗證，并研究了大柔性機翼的極限環顫振特性。研究表明：適用于大柔性機翼完整的非線性氣動彈性建模需要考慮機翼結構大變形和非定常氣動力動態失速等非線性因素；彎曲變形可降低臨界極限環顫振速度的15%以上，而前移彈性軸能夠有效的提高臨界極限環顫振速度；所提出的非線性氣動彈性求解方法具有較好的精度和效率，滿足大柔性機翼非線性氣動彈性的求解需求。

關鍵詞：非線性氣動彈性；極限環顫振；CR理論；非定常氣動力；動態失速；Newmark積分法

中圖分類號:V211.47

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.19.010

Abstract:Very flexible wings under aerodynamic loads tend to produce larger deformation, it results in significant changes in inertial and stiffness characteristics, and dynamic aeroelastic features, the linear aeroelastic analysis method is no longer applicable. Here, based on the co-rotational(CR) theory, the tangent stiffness matrix and mass matrix of a wing after deformation were derived, the structural dynamic model of very flexible wings considering geometric nonlinearity was then established. Coupled with ONERA dynamic stall model, an efficient method to solve nonlinear aeroelasticity of very flexible wings was proposed. Using Newmark direct integration method and loose coupled algorithms, a numerical procedure for solving nonlinear aeroelastic dynamic equations was presented, and the efficiency and precision of the method were verified through tests. The results showed that structural and aerodynamic nonlinearities should be considered for complete nonlinear dynamic aeroelastic simulations of very flexible wings; the wing’s critical limit cycle oscillation speed decreases 15% or more due to its bending deformation, but it increases through shifting forward the wing’s elastic axis; the proposed method has a good precision and efficiency, and meets requirements of nonlinear aeroelastic analysis of very flexible wings.

基金項目：國家自然科學基金(51475387)

收稿日期：2014-06-12修改稿收到日期：2014-09-30

A CR theory-based approach for solving nonlinear aeroelasticity of very flexible wings

WANGWei1,ZHOUZhou1,ZHUXiao-ping2,WANGRui1(1. College of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China；2. UAV Research Institute, Northwestern Polytechnical University, Xi’an 710065, China)

Key words:nonlinear aeroelasticity; limit cycle oscillation; CR theory; unsteady aerodynamics loads; dynamic stall; Newmark integration method

高空超長航時太陽能無人機在飛行高度上能夠填補低軌道衛星和常規能源飛機的空白，執行環境監測、通信中繼等任務，具有覆蓋區域廣、持續時間長和花費低等特點，由于高空長航時的性能要求，這類飛機一般具有較小的結構重量和超大展弦比機翼，在氣動載荷的作用下，機翼彎曲變形可達半翼展的50%，機翼的結構動力學特性和氣動彈性特性隨變形的增加而產生較大改變。建立高精度的大柔性機翼結構動力學模型進而盡可能高精度、高效率的預測大柔性大變形機翼的非線性氣動彈性特征是這類飛機的主要研究內容之一。由于面內、面外彎曲變形和扭轉變形與結構當前的幾何位形有關，并且機翼局部剖面的有效攻角可能很大，這類機翼的氣動彈性建模需要考慮結構幾何非線性和大攻角時非定常氣動力動態失速的影響。

目前考慮幾何非線性效應的非線性氣動彈性運動方程的求解方法主要有直接數值積分法和線性化后的頻域法[1-6]。直接數值積分法可以考慮結構大振幅運動以及氣動力的動態失速效應等非線性因素；線性化的頻域法一般假設結構在靜平衡位置附近作小振幅振動，然后耦合線性頻域非定常氣動力，采用經典的P-K法或V-g法求解而無法考慮氣動非線性的影響[5]。Patil等[4]基于經典ONERA動態失速模型建立了可以描述二維翼段準靜態失速的非線性非定常氣動力模型，并耦合混合變分形式的彎-彎-扭耦合本征梁模型建立了非線性氣動彈性運動方程，開展了針對大柔性機翼的非線性氣動彈性的研究。Shams等[6]采用Duhamel積分形式的Wagner函數描述線性時域非定常氣動力并耦合非線性Euler-Bernouli理論梁模型建立了描述大柔性機翼的非線性氣動彈性運動方程，沒有考慮動態失速效應引起的非線性效應。非線性理論梁模型固然具有高精度、高效率等優點，但物理變量不直接，通用性受到一定的限制。隨著非線性有限元技術的發展，謝長川等[5]基于線性化的UL有限元理論對復雜結構機翼的非線性顫振問題開展了大量研究，氣動彈性運動方程在頻域內求解，而無法預測臨界速度前后的結構運動行為；在時域內采用TL法或UL法求解結構動力學方程時為了獲得較好的精度一般選擇非常小的時間步長，從而顯著地增加求解時間；隨著CR有限元技術的發展，其靜力學求解允許適度大的載荷步、動力學方程求解同樣允許適度大的時間步，從而引起了許多學者基于CR列式法對有限旋轉問題的研究[7-13]。作者在大柔性太陽能無人機的靜氣動彈性研究中，引入了CR非線性有限元梁模型描述機翼的幾何大變形，減少了流固耦合迭代次數，取得了較好的效果[14]。

本文在所編寫的大柔性結構幾何非線性靜力學求解程序的基礎上，進一步推導了空間CR梁單元的結構動力學方程，首先以懸臂梁模型為例，研究了大柔性結構在外載荷作用下的強迫振動，驗證了基于CR有限元理論所建立的結構動力學模型的精度、效率及所編寫程序的正確性。其次，以簡諧振蕩的NACA0012翼型為例，采用改進的ONERA動態失速模型對典型翼段的非線性非定常氣動力進行求解，驗證了非定常非線性氣動力模型對動態失速效應模擬的精度。最后，耦合上述結構動力學模型和非線性非定常氣動力模型，基于松耦合求解技術，提出了一種適用于幾何大變形大柔性機翼的非線性氣動彈性求解方法，并研究了大柔性機翼的極限環顫振特性以及彈性軸站位對極限環顫振的影響等。

1大柔性機翼結構動力學建模

大柔性機翼在氣動載荷的作用下，變形前后的幾何位形具有明顯的差異，常規的線彈性小變形假設不再成立，而局部結構的材料應力應變關系仍處于線彈性范圍內。CR有限元法的主要思想是將結構的變形分為剛體的旋轉及平移和單元坐標系內的線彈性變形，平衡方程在單元坐標系內建立，通過坐標轉換矩陣及其微分形式構造總體坐標系下的切線剛度矩陣，因而其核心是坐標轉換矩陣的建立及其微分形式的推導，其計算精度主要取決于剛度矩陣和坐標系轉換矩陣對幾何非線性描述的精確性。

1.1CR梁單元靜力學平衡方程

CR有限元理論的平衡方程建立在單元坐標系內，通過總體坐標系Ixyz、節點坐標系ui和單元平均構形坐標系um建立單元坐標系ue，見圖1。

結構位形確定后，單元節點的三個歐拉角和現時坐標隨之確定，按照式(1)旋轉總體坐標系得到節點坐標系：

ui(x)=Ti(x)Ixyz

(1)

那么參照文獻[9,14]，CR空間梁單元的單元坐標系定義為：

ue1=(d2-d1)/ln

ue2=um2-((uTm2ue1)/2)(ue1+um1)

ue3=um3-((uTm3ue1)/2)(ue1+um1)

(2)

式中，d1與d2分別是節點i,j的現時坐標ln=[(d2-d1)T(d2-d1)]1/2。

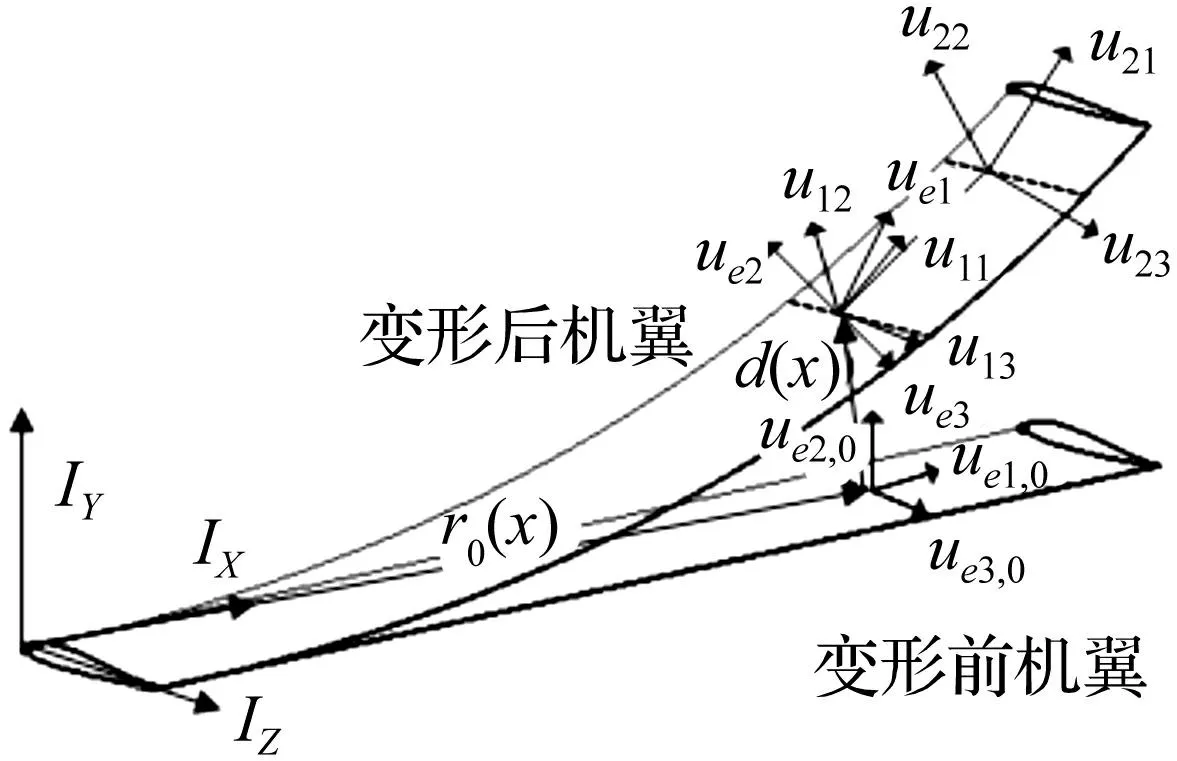
圖1　柔性結構變形示意圖 Fig.1 Sketch of a deformed very flexible structure

可見節點坐標系和單元坐標系都是結構位形的函數，在求解過程中需要隨變形的增加而不斷更新。

CR有限元法充分利用了幾何非線性問題的小應變、大位移特征，彈性變形在單元坐標系內描述，位移-應變關系仍然是線性的。利用方程2建立的單元坐標系與方程1建立的節點坐標系，得到單元坐標系下的節點位移：

ul=ln-lo

2θl1,1=-uTi3ue2+uTi2ue3

2θl1,2=-uTi1ue3+uTi3ue1

2θl1,3=-uTi2ue1+uTi1ue2

2θl2,1=-uTi3ue2+uTi2ue3

2θl2,2=-uTi1ue3+uTi3ue1

2θl2,3=-uTi2ue1+uTi1ue2

(3)

對式(3)進行微分得到單元坐標系下位移增量δpl到總體坐標系下位移增量δp的坐標轉換矩陣T：

δpl=Tδp

(4)

總體坐標系下廣義節點力向量f為：

f=TTfl=TTKlpl

(5)

δf=δTTKlpl+TTKlδpl=

[KTσ(fl)+TTKlT]δp

(6)

增量平衡方程為：

KTΔp=ΔFe

(7)

KT=KTσ(fl)+TTKlT為所求的切線剛度矩陣，其中TTKlT為材料剛度矩陣，KTσ(fl)為幾何剛度矩陣，是單元坐標系下單元節點力fl的函數。

當大柔性機翼上布置有發動機等推進系統時，將會引入隨動力進而影響機翼的顫振穩定性[17]。假設該發動機掛載在第i個節點下，Fs(t)表示總體坐標系下隨動載荷等效到節點i處的外載荷。那么，第i個節點的總外載荷可以描述為：

Fi,e(t)=Fi,a(t)+Fs(t)

(8)

當隨動載荷描述在局部坐標系下時，需要把Fs,i(t)轉換到總體坐標系下，轉換表達式為：

Fs(t)=Ui,IFs,i(t)

(9)

具體求解時需要注意，隨結構運動需要實時更新轉換矩陣Ui,I。

1.2CR梁單元動力學平衡方程

大柔性機翼在變形的過程中可以認為其局部翼剖面沒有發生翹曲[4，6]，則剖面內所有點具有相同的角速度，截面線動量與角動量為：

(10)

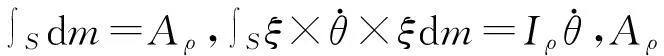
那么，截面慣性力和慣性力矩可以表示為：

(11)

截面剛心處的線加速度、角速度和角加速度依次通過節點線加速度、角速度和角加速度插值得到：

(12)

同樣可以插值得到截面虛位移，那么慣性力在虛位移上所做的虛功為：

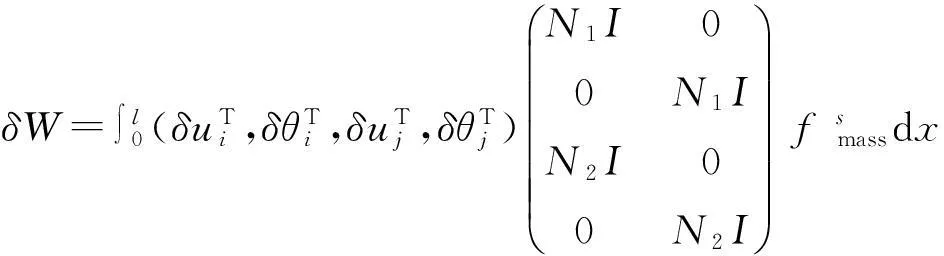
(13)

根據虛功原理，等效節點慣性力所做的虛功為：

δW=f Tmass(δuTi,δθTi,δuTj,δθTj)T

(14)

把方程13代入式(14)得：

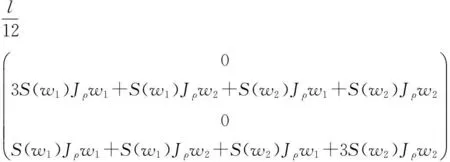
由方程(15)可以看出，線加速度是定義在總體坐標系下的，而角加速度是定義在單元坐標系下的，并且慣性力與時間和結構位形有關。

根據方程(15)所得到的慣性力表達式，忽略阻尼后考慮幾何非線性效應的大柔性結構動力學平衡方程可以表示為：

Fe-fmass-fi=0

(16)

式中，Fe表示結構t時刻所受的外載荷，fmass表示結構t時刻的慣性力，fi表示結構t時刻的內力，它們均與時間t有關。

1.3非線性動力學平衡方程的時域推進求解

采用隱式Newmark時域積分格式求解大柔性機翼的結構動力學問題時，需要考慮系統在tn+1時的平衡，并采用Newton-Raphson法迭代求解控制平衡方程。Newmark積分法可以認為是對線性加速度法的推廣，其插值假設是：

(17)

式中，ΔΨ=UTnΔψ，為隨動坐標系下描述節點坐標系Un旋轉到Un+1所對應的旋轉偽矢量；Δψ為總體坐標系下描述節點坐標系Un旋轉到Un+1所對應的旋轉偽矢量。

根據上述假設，對方程15進行微分，得：

δfmass=δ([Ue]fmass,in)=MT,massδp

(18)

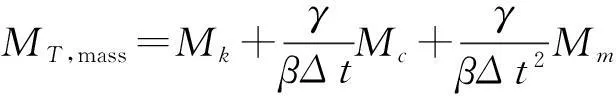
根據方程(18)得到慣性力的切線表達形式，可以采用預估校正技術求解方程(16)。預估的本質是用tn時刻位移及增量斜率預測tn+1時刻的位移。第一次位移增量Δp0可以通過下式預估求解得到：

(19)

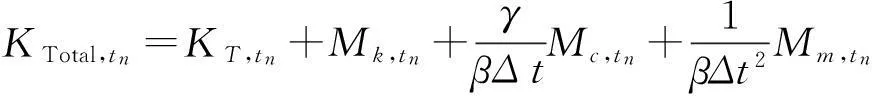
將預估求解得到的位移增量代入方程式(16)，計算tn+1時刻第k次迭代后的非平衡力：

(20)

校正步內采用下式迭代求解，直到滿足收斂標準：

gk=(KkT,tn+1+MkT,tn+1)Δpk

(21)

與靜力學增量平衡方程的求解基本一致，采用預估校正推進技術求解方程式(16)時，在校正步內一般采用Newton-Raphson或修正的Newton-Raphson迭代求解，只是動力學求解中殘差gk隨所求解的時間步內位移增量的更新而不斷更新。

2非線性非定常氣動力模型

采用ONERA動態失速模型描述非線性非定常氣動力，在不同文獻中，其表達式形式也不盡相同；這里采用改進的ONEAR(EDLin)動態失速模型[18]。非定常升力、力矩作用在四分之一弦長處，表達式為：

(22)

(23)

(24)

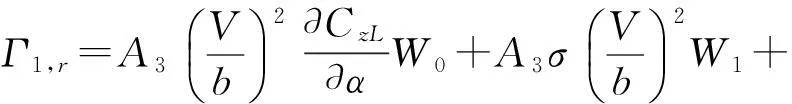
把式(23)和(24)寫成緊湊矩陣形式：

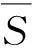
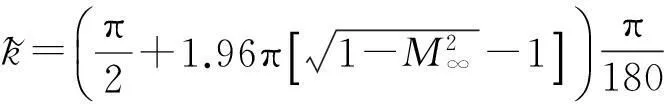
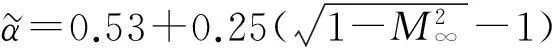
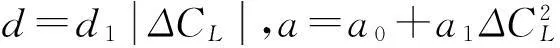
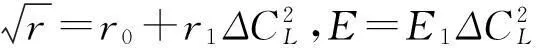
(25)

(26)

把式(26)寫成緊湊矩陣形式：

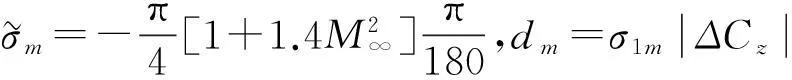
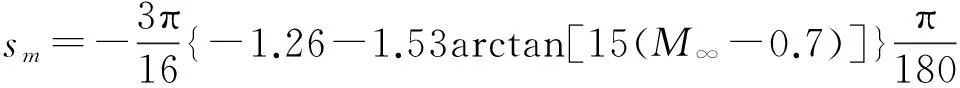
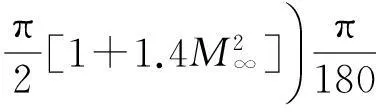
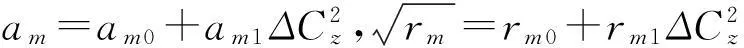
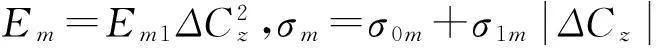
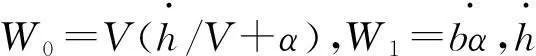
采用四級四階Runge-Kutta公式求解改進的ONERA動態失速模型中的微分方程，求解格式為：

(27)

3非線性氣動彈性運動方程

第二節中的動力學方程求解是以總體坐標系下的節點線位移、角位移、線速度、線加速度和單元坐標系下角速度、角加速度為未知量的；非線性非定常氣動力的求解輸入是局部氣流坐標系下的片條沉浮線位移、線速度、線加速度、角位移、角速度、角加速度等，因此需要對動力學模型的解向量進行轉換和插值。

首先繞Iy旋轉90°，再繞現在的x軸旋轉90°得到總體氣流坐標系，再繞總體氣流坐標系的負x軸旋轉θ得到局部氣流坐標系：

(28)

那么總體坐標系下的線位移、角位移、線加速度、角加速度和單元坐標系下的角速度及角加速度到局部氣流坐標系下的轉換關系式為：

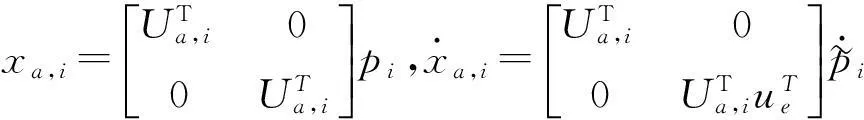
(29)

經過插值得到每個片條的振動及沉浮、扭轉運動：

(30)

根據式(19)和(23)計算得到局部氣流坐標系下的片條非定常氣動力Qs，然后根據功互等原理，將片條在局部氣流坐標系下的非定常氣動載荷按照等效節點力的形式插值到相鄰節點上，計算公式為：

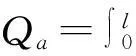
(31)

采用下式把局部氣流坐標系下的節點力轉換到總體坐標系下：

(32)

對式(32)得到的節點氣動力組裝后可以得到總體坐標系下的非定常氣動力Qe，代入方程(16)代替外載荷向量Fe，可以得到機翼的氣動彈性運動方程：

Qe-fmass-fi=0

(33)

在時域內對式(33)進行直接數值積分求解時，與結構動力學求解中tn+1時刻的外載荷已知不同，tn+1時刻的非定常氣動力Qe與tn+1時刻的結構運動狀態有關，因而需要預估tn+1時刻的非定常氣動力，然后根據解得的tn+1時刻的結構狀態更新非定常氣動力，根據Newton等距向前插值多項式進行外推：

Qe,tn+1=3Qe,tn-3Qe,tn-1+Qe,tn-2

(34)

松耦合的求解思想是：首先預估下一時刻的非定常氣動力，然后帶入氣動彈性運動方程中求解結構運動狀態，以解得的下一時刻結構狀態重新計算非定常氣動力代替預估值，但不參與迭代求解，而是直接推進到下一時間步的求解；若參與迭代求解，上述計算方法則變成緊耦合推進求解算法。緊耦合迭代求解算法具有精度高的優點但求解易發散，一般很少在非線性氣動彈性系統的求解中使用。綜上所述，松耦合推進求解方程式(33)的流程見圖2。

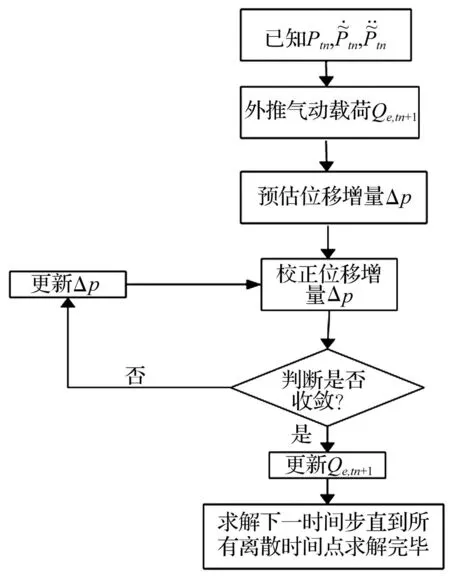
圖2　非線性氣動彈性系統松耦合求解流程 Fig.2 Calculation process of the nonlinear aeroelastic system based on loosely coupled technology

4算例及驗證

大柔性機翼非線性氣動彈性求解所需的幾何參數、剛度參數、質量參數及大氣參數見表1。

4.1大柔性懸臂梁幾何非線性動力學求解

首先把大柔性機翼作為懸臂梁，不考慮氣動力的作用，在翼尖施加集中載荷歷程見圖3(b)，分別采用經典UL法(時間步長為1E-4s)和CR法(時間步長為5E-2s)進行求解，以驗證基于CR有限元法采用直接數值積分技術(Newmark法)求解大柔性結構動力學響應的精度等。

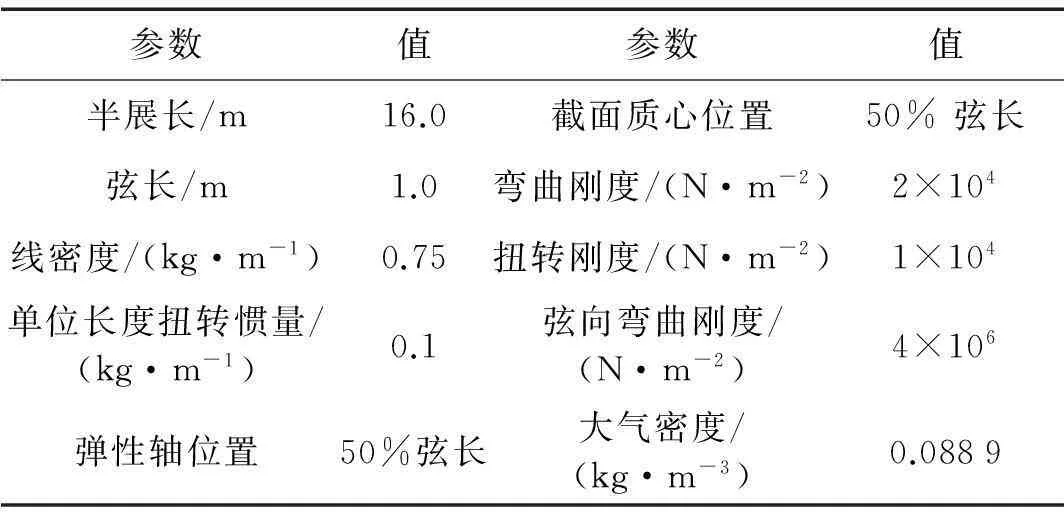
表1　大柔性機翼模型參數 [4]

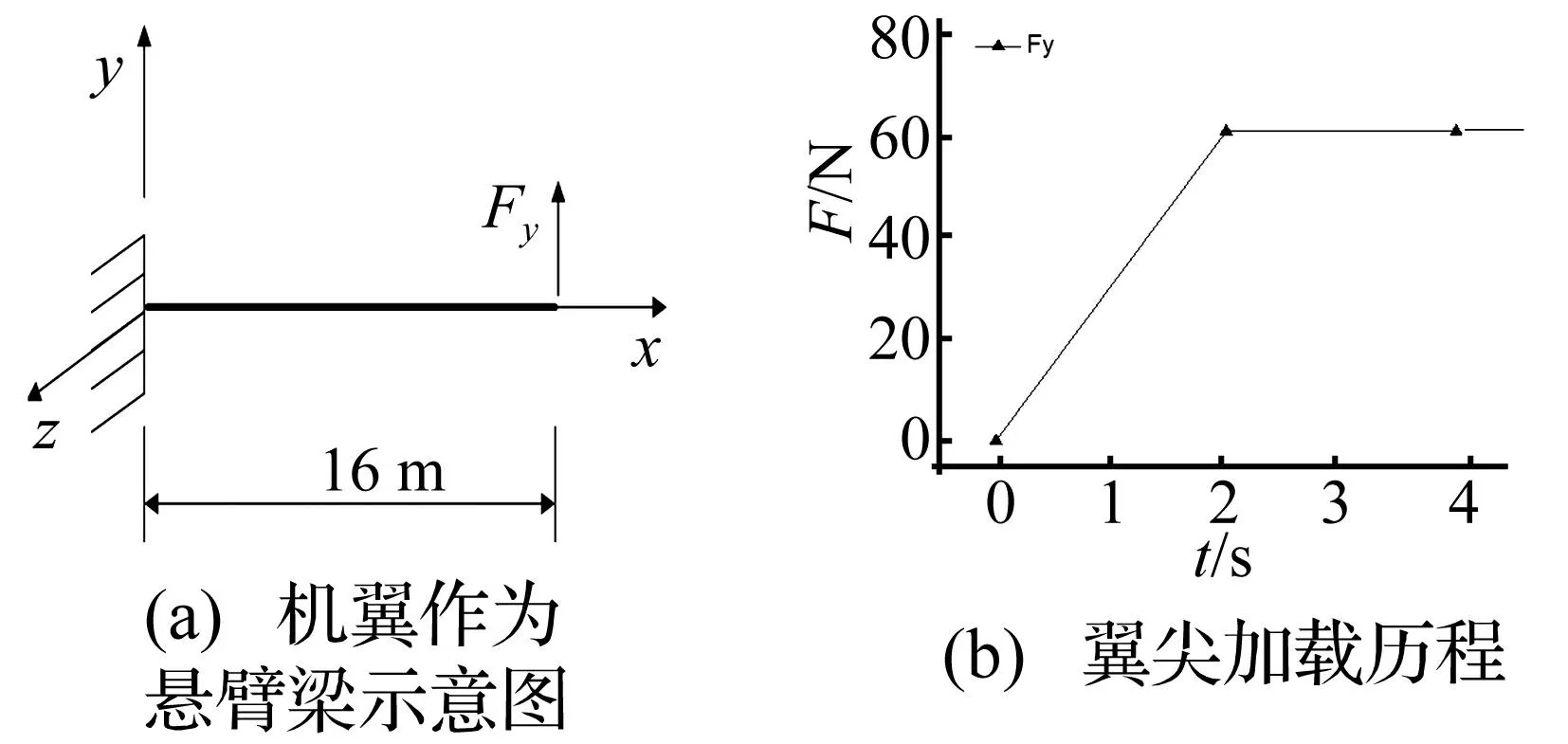
圖3　大柔性懸臂梁及其端部加載示意圖 Fig.3 Sketch of a very flexible cantilever beam and the tip loading history

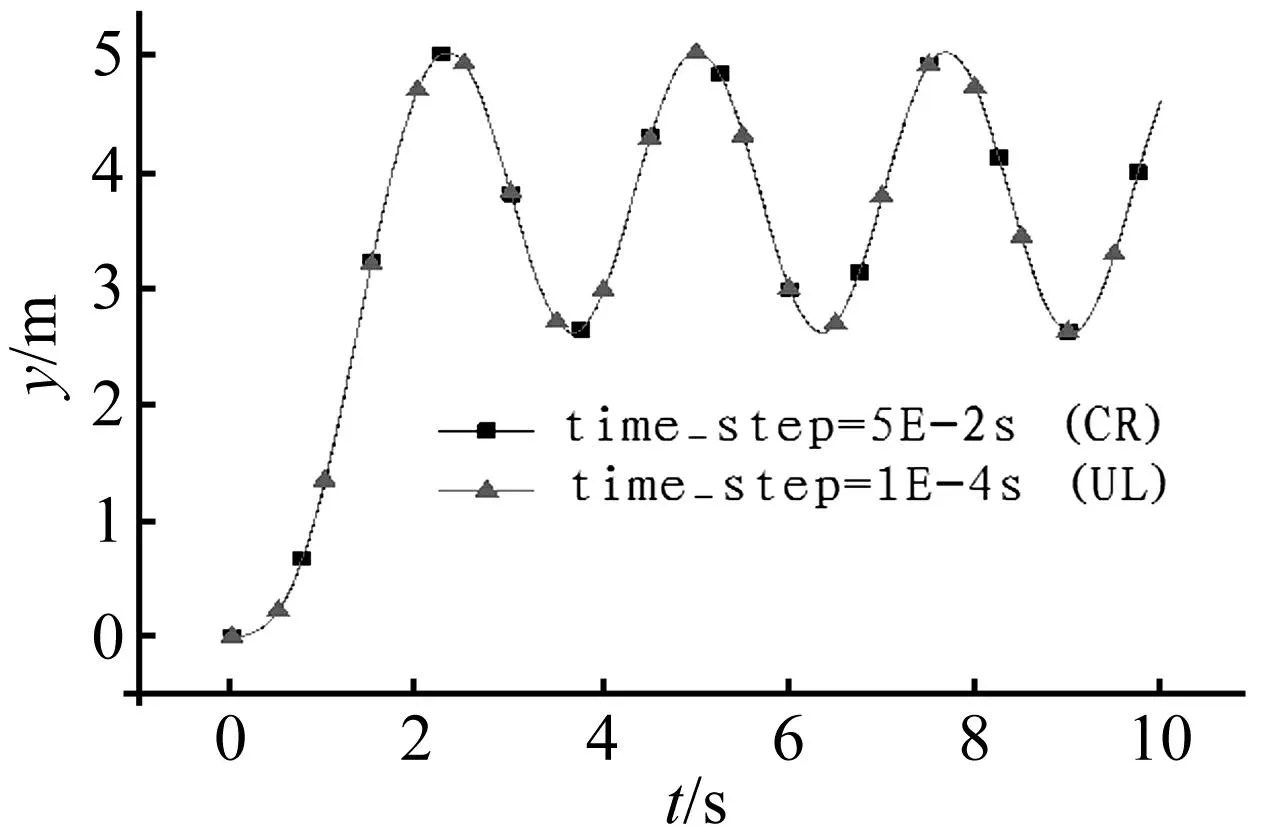
圖4　不同步長下CR法與UL法求解結果對比 Fig.4 Results comparing between CR method and UL method under variant time steps

由圖4中的計算結果可以看出，采用CR法求解大柔性結構的動力學響應問題時允許采用較大的時間步長，且具有較好的求解精度，滿足大柔性機翼結構動力學求解對幾何非線性因素的描述精度要求。

4.2非線性非定常氣動力模型驗證

以NACA0012翼型為例，采用ONERA動態失速模型及其改進形式對非定常非線性氣動力進行求解，結果見圖5。

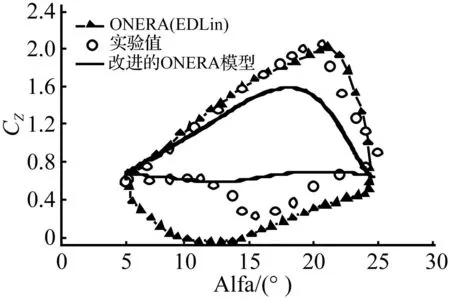
圖5　α=15°+10° cos(0.1τ)的非定常氣動力 Fig.5 Unsteady aerodynamics atα=15°+10° cos(0.1τ)

大迎角區域內，經典的ONERA(EDLin)模型求解精度較好，而改進后的ONERA模型雖然略微降低了對大迎角區的模擬精度但是顯著的改善了小迎角區的求解精度。

仍然以NACA0012翼型為例，平均迎角分別取6°、12°、17°，h=0.1sin(0.1τ)m，τ=Vb/t；采用改進的ONERA動態失速模型研究完全線性段、部分線性段部分非線性段及完全非線性段內的非定常氣動力特性，得到翼段純沉浮運動下的非定常氣動力見圖6。

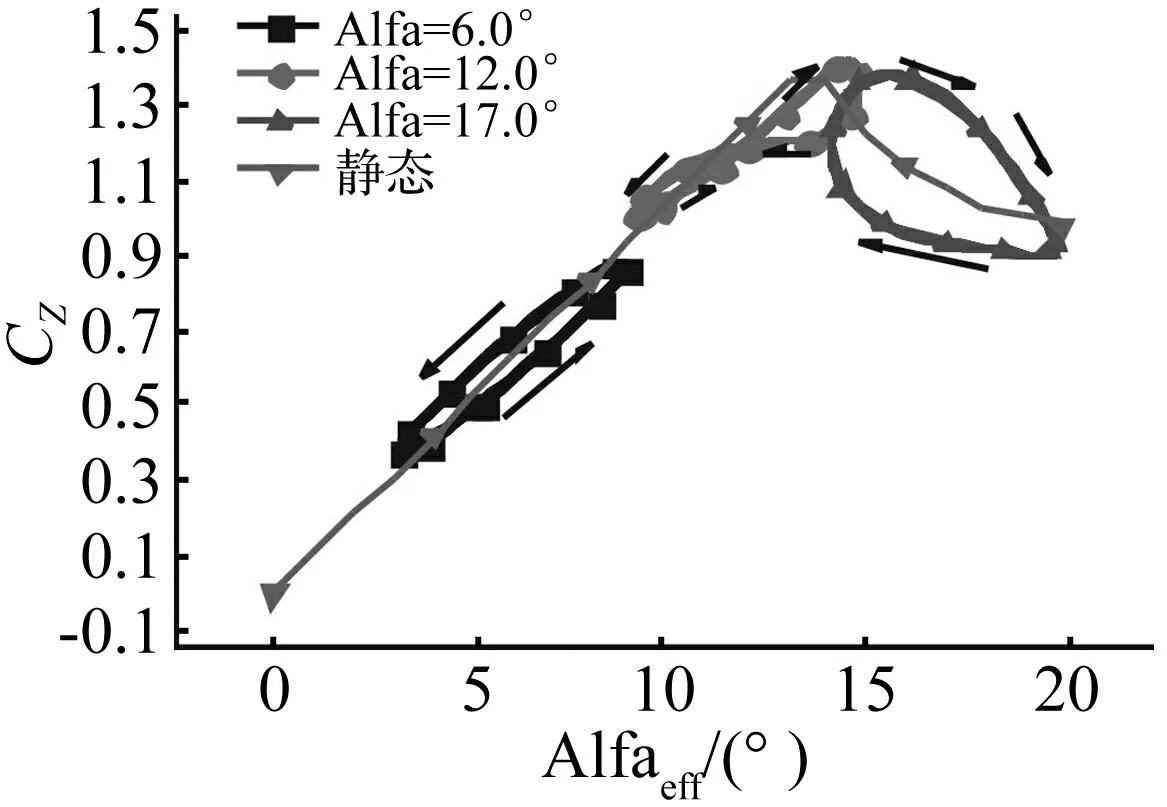
圖6　h=0.1sin(0.1τ)m的非定常氣動力 Fig.6 Unsteady aerodynamics at h=0.1 sin (0.1τ)m

可見采用改進的ONERA模型無論是線性段還是非線性段均可以較好的模擬二維機翼的非定常氣動力，特別是非線性段的動態失速效應。

4.3大柔性機翼非線性氣動彈性響應求解

以表1中所給出的大柔性機翼為例，機翼剖面為NACA0012翼型，初始翼尖彎曲位移為4m時，本文與文獻4及文獻6得到的臨界極限環顫振速度均約為28m/s，翼尖位移響應歷程與文獻值的對比見圖7示。

圖7　V=28m/s，y 0=4.0m時翼尖彎曲位移響應 Fig.7 Wingtip displacement response at V=28m/s，y 0=4.0m

從圖7可以看出，采用所提出的非線性氣動彈性求解方法解得的位移響應與文獻值6吻合的更好，可能是因為文獻4中沒有考慮非定常氣動力的動態失速效應。翼尖位移響應的相位圖見圖8。

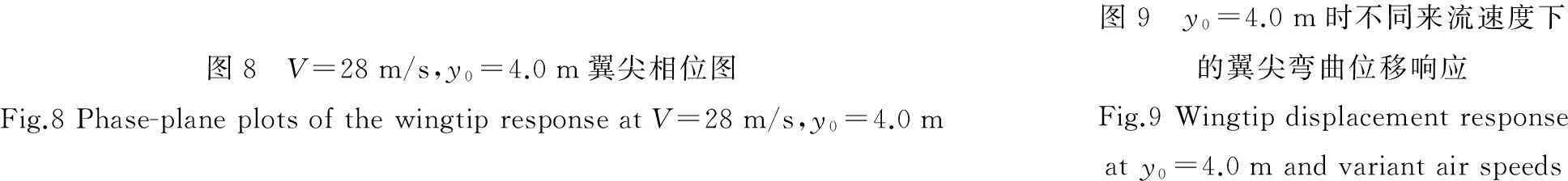
圖8 V=28m/s,y0=4.0m翼尖相位圖Fig.8Phase-planeplotsofthewingtipresponseatV=28m/s,y0=4.0m圖9 y0=4.0m時不同來流速度下的翼尖彎曲位移響應Fig.9Wingtipdisplacementresponseaty0=4.0mandvariantairspeeds

圖10　y 0=4.0m時不同來流速度下的翼尖響應相位圖 Fig.10 Phase-plane plots of the wingtip response at y 0=4.0m and variant air speeds

由計算結果可以看出，采用所提出的非線性氣動彈性求解方法可以較好的預測大柔性機翼的極限環顫振。進一步增加來流速度，研究來流速度大于臨界速度時的大柔性機翼非線性氣動彈性響應特性；初始彎曲位移為4.0m。

由計算結果可以看出，當來流速度略大于28m/s時，大柔性機翼的氣動彈性翼尖位移響應仍具有周期性，當來流速度增加到32m/s時，翼尖位移響應不再具有周期性。隨來流速度的增加，翼尖彎曲位移響應及扭轉響應幅值隨之增加，且極限環顫振變得越來越復雜。來流速度為28m/s時，極限環顫振每個周期的振動幅值一致，但來流速度增加后，翼尖位移響應需要經過一個幅值較小的周期和一個幅值較大的周期才能夠回到原位置。另外，從圖10中還可以看出隨來流速度的增加，局部動態失速效應越來越明顯。

4.4彈性軸站位對大柔性機翼極限環顫振的影響

給定初始條件下，誘發非線性氣動彈性極限環顫振的最小速度稱為臨界極限環顫振速度[4]。結構參數仍以表一中給出的參數作為基準不變，研究彈性軸和剖面質心一起向前緣移動時對臨界極限環顫振速度的影響。初始翼尖彎曲位移分別選為4m、3m、2m、1m，得到的臨界極限環顫振速度隨彈性軸在弦向站位的不同而增減的趨勢見圖11。

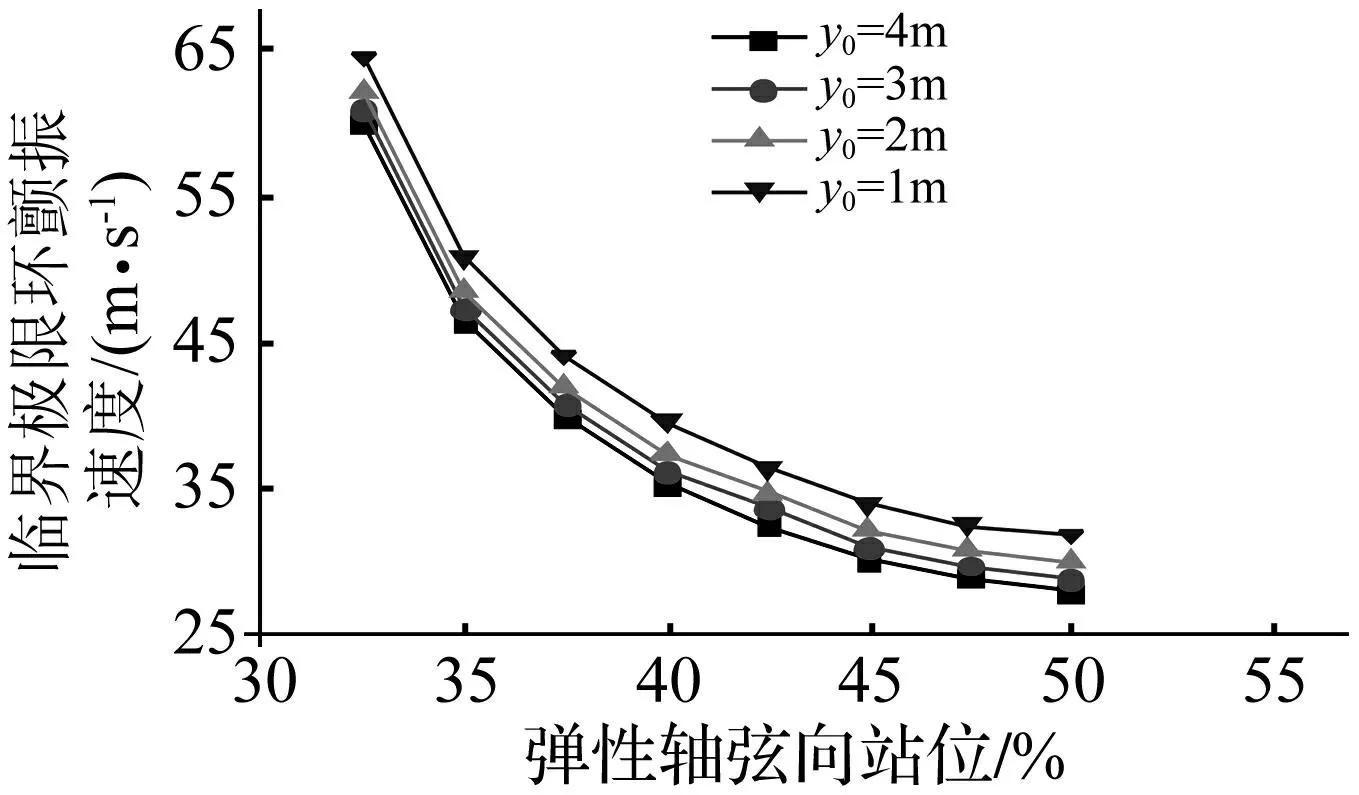
圖11　彈性軸站位對極限環顫振的影響 Fig.11 The effects on limit cycle oscillation due to variant elastic axis positions

從圖11中可以看出，翼尖彎曲位移的增加將降低機翼的臨界極限環顫振速度；彈性軸在50%的弦長處時，初始翼尖彎曲位移為4m時解得的臨界極限環顫振速度與初始翼尖彎曲位移為1m時相比降低了15.36%；另外，彈性軸的前移可以有效的提高臨界極限環顫振速度；因此，對于這類大柔性機翼，通過合理設計彈性軸的弦向站位，可以有效的改善彎曲變形對機翼氣動彈性所引起的不利效應。

4.5積分步長的選擇及收斂性

直接數值積分的收斂性和精度可以通過不同時間步長的選取以證明，在上述研究中時間步長均為0.005s，這里進一步補充來流速度為28m/s時，初始彎曲位移為4m，時間步長為0.01s和0.0001s的計算結果。

圖12　不同時間步長的積分結果 Fig.12 Comparing of direct integration results between variant time steps

從圖12中可以看出，時間步長為0.005s和0.0001s的積分結果基本一致，因此時間步長選為0.005s滿足計算精度的要求，并且與時間步長為0.0001s時相比大大減少了求解時間。針對具體的求解問題，對比不同的積分步長對求解精度和穩定性的影響，指導選擇合適的積分步長，可以有效地提高求解效率；具體執行時，可選擇下一次積分步長為本次積分步長的1/N(N為大于等于2的整數)，兩次求解得到的最大響應幅值相差小于幅值的5%時，即可把本次試算積分步長作為采用直接數值積分求解目標算例的較為合理的時間積分步長。

5結論

本文基于CR有限元非線性動力學求解技術和改進的ONERA動態失速非線性非定常氣動力模型提出了一種適用于大柔性大變形機翼的非線性氣動彈性求解方法，進而對大柔性機翼的非線性氣動彈性響應特性進行了較為深入的研究，主要得到以下結論：

(1)本文所提出的非線性氣動彈性響應計算方法，以總體坐標系下的位移等為變量，物理意義簡單直接，具有較好的求解精度和計算效率，能夠滿足大柔性機翼非線性氣動彈性響應求解的需求，并可以較好的預測大柔性機翼的極限環顫振。

(2)較小的時間步長可以提高求解的精度但計算花費隨之增加，在具體的求解中可以預先對比不同積分步長對求解精度的影響，指導選取合適的積分步長，以滿足求解的需求。

(3)來流速度大于臨界極限環顫振速度時，大柔性機翼的非線性氣動彈性響應是非常復雜的，非定常氣動力的動態失速效應雖然限制了振幅的增加，但也會帶來結構疲勞等問題，在這類機翼的結構設計時需要特別注意。

(4)前移彈性軸可以有效地提高臨界極限環顫振速度，增加周期性極限環顫振的速度區間，顯著地改善大柔性機翼的非線性氣動彈性特性，可以用于指導大柔性機翼彈性軸在弦向的站位設計。進一步的研究工作中可以引入高效的預估求解算子，減少動力學響應求解時的迭代次數，提高求解效率。

參考文獻

[1]Patil M J, Hodges D H. On the importance of aerodynamic and structural geometrical nonlinearities in aeroelastic behavior of high-aspect-ration wings[J].Journal of Fluids and Structures,2004,19:905-915.

[2]Patil M J, Hodges D H, Cesnik C E S. Nonlinearaeroelasticity and flight dynamics of high-altitude long-endurance Aircraft [R]. AIAA-99-1470.

[3]Patil M J, Hodges D H. Flightdynamics of highly flexible flying wings [J]. Journal of Aircraft，2006，43(6):1790-1798.

[4]Patil M J, Hodges D J, Cesnik C E S. Limit cycle oscillations in high-aspect-ratio wings[J].Journal of Fluid and Structures,2001,15:107-132.

[5]Xie Chang-chuan, Yang Chao. Linearization methods of nonlinear aeroelastic stability for complete aircraft with high-aspect-ratio wings[J]. Sci China Tech Sci,2011, 54:403-411.

[6]Shams S, Sadr M H, Haddadpour H.An efficient method for nonlinear aeroelasticy of slender wings[J].Nonlinear Dynamics,2012,67:659-681.

[7]周凌遠，李喬.基于UL法的CR列式三維梁單元計算方法[J]. 西南交通大學學報，2006，41(6):690-695.

ZHOU Ling-yuan, LI Qiao. Updated lagrangian co-rotational formulation for geometrically nonlinear FE analysis of 3D beam element[J].Journal of Southwest Jiaotong Unoversity,2006,41(6):690-695.

[8]Belytschko T, Schwer L. Large displacement, transient analysis of space frames[J]. International Journal for Numerical Methods in Engineering, 1977, 11:65-84.

[9]Crisfield M A. A consistent Co-rotational formulation for non-linear, three-dimensional, beam element[J]. Computer Methods In Applied Mechanics And Engineering, 1990,81:131-150.

[10]Crisfield M A. Non-linear finite element analysis of solids and structures, Volume 2: Advanced topics[M]. John Wiley & Sons, Chichester, New York, Weinheim, Brisbane, Singapore, Toronto,2000.

[11]Crisfield M A,Galvanetto U, Jelenicé G. Dynamics of 3-D co-rotational beams[J]. Computational Mechanics, 1997,20：507-519.

[12]Ghosh S, Roy D. Consistent quaternion interpolation for objective finite element approximation of geometrically exact beams[J]. Computer Methods In Applied Mechanics And Engineering,2008, 198:555-571.

[13]Le T N, Battini J M, Hjiaj M. Dynamics of 3d beam elements in a corotational context: a comparative study of established and new formulation[J]. Finite Elements in Analysis and Design,2012,61:97-111.

[14]王偉,周洲,祝小平,等.考慮幾何非線性效應的大柔性太陽能無人機靜氣動彈性分析[J]. 西北工業大學學報, 2014, 32(4):499-504.

WANG Wei, ZHOU Zhou, ZHU Xiao-ping,et al. Static aeroelastic characteristics analysis of a very flexible solar powered UAV with geometrical nonlinear effect considered[J]. Journal of Northwestern Polytechnical University, 2014, 32(4):499-504.

[15]Palacios R, Murua J, Cook R. Structural and aerodynamic models in nonlinear flight dynamics of very flexible aircraft [J]. AIAA Journal, 2010,48 (11):2648-2659.

[16]吳國榮,顏桂云，陳福全.柔性梁大柔度動力響應分析的多體系統方法[J].振動與沖擊,2007,26(3):87-89.

WU Guo-rong,YAN Gui-yun,CHEN Fu-quan.Large deflection dynamic response analysis of flexible beams bi multibody system method[J].Journal of Vibration and Shock, 2007,26(3):87-89.

[17]張健,向錦武.側向隨動力作用下大展弦比柔性機翼的穩定性[J].航空學報,2010,31(11):2115-2123.

ZHANG Jian, XIANG Jin-wu. Stability of high-aspect-ratio fiexible wings loaded by a lateral follower force[J].Chinese Journal of Aeronautics,2010,31(11):2115-2123.

[18]Laxman V,Venkatesan C.Chaotic response of an airfoil due to aeroelastic coupling and dynamic stall[J].AIAA Jourmal, 2007,45(1):271-280.

第一作者何洪陽男，碩士，1988年生

通信作者陳春俊男，博士，教授，1967年生