數控機床進給單元滾動結合部軸向動態特性參數識別

第一作者朱堅民男，博士，教授，博士生導師，1968年生

數控機床進給單元滾動結合部軸向動態特性參數識別

朱堅民，張統超，王健，李孝茹

(上海理工大學機械工程學院，上海200093)

摘要：針對現有結合部參數識別方法不能精確識別裝配狀態下數控機床進給單元滾動結合部動態特性參數問題，提出進給單元裝配狀態下滾動結合部軸向動態特性參數識別方法。將絲杠簡化為彈性桿件以建立簡諧力作用下絲杠及工作臺的軸向振動方程，基于該方程建立結合部軸向剛度與阻尼參數識別模型；通過實驗測量絲杠支撐點間距離、簡諧激振力頻率及幅值、絲杠軸端截面軸向振動速度幅值等參數建立識別方程組；基于遺傳算法優化求解該方程組，識別出滾動結合部軸向動態特性參數。以自行研制的滾珠絲杠進給實驗臺為研究對象，基于該方法對其左、右端軸承組及滾珠絲杠副結合部軸向剛度、阻尼參數進行識別，并對識別結果的正確性進行實驗驗證。結果表明所提方法正確、有效，絲杠軸端截面軸向振動速度幅值的理論計算值與實驗測試值絕對誤差在7.7 μm/s以內，參數識別精度較高。

關鍵詞：滾珠絲杠進給單元；滾動結合部；動態特性參數識別；振動測試；遺傳算法

基金項目：國家自然科學基金資助項目(50975179)；上海市教委科研創新資助項目(11ZZ136)；上海市科委科研計劃資助項目(13160502500)；滬江基金(D14005)

收稿日期：2014-11-17修改稿收到日期：2015-03-17

中圖分類號:TH113.1文獻標志碼：A

Axial dynamic characteristic parameters identification of rolling joints in machine tool feed drive unit

ZHUJian-min,ZHANGTong-chao,WANGJian,LIXiao-ru(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

Abstract:In allusion to the problem that the existing methods for joint’s parameters identification cannot accurately identify the dynamic characteristic parameters of rolling joints in assembled ball screw feed drive unit, a novel method to identify the axial stiffness and damping parameters of rolling joints was proposed. In the method, the screw was simplified as an elastic rod and the axial vibration equations of the feed drive unit under the excitation of harmonic force were derived, the identification model of the joints’ axial stiffness and damping parameters was created, the identification equations were established based on measuring the distance between supporting points of the screw, the frequency and amplitude of harmonic exciting force, and the amplitude of axial vibration velocity at the screw end section, and then the axial stiffness and damping parameters of the rolling joints were identified by solving the identification equations using genetic algorithm. Taking a self-designed ball screw feed drive test bench as the research object, the axial stiffness and damping parameters of its ball screw assembly, and its left and right bearing groups were identified by using the proposed method, and the correctness of identified results was verified by experiments. The results demonstrate that the proposed method is correct and effective, and the absolute error of axial vibration velocity at screw end section between the calculated and tested values is within 7.7 μm/s, which achieves high identification accuracy.

Key words:ball screw feed drive unit; rolling joints; dynamic characteristic parameters identification; vibration measurement; genetic algorithm

滾珠絲杠進給單元為高速、高精度數控機床常用進給形式之一[1-2]，它是由滾珠絲杠副、滾動導軌副、軸承、工作臺等零部件組成的復雜機電耦合系統，其綜合動態性能不僅取決于各組成零部件，且與結合部動態特性參數直接關聯[3]。研究表明，結合部剛度、阻尼為滾珠絲杠進給單元理論建模[4]、動態特性優化[5]及伺服控制系統設計[6]等關鍵參數。正確識別結合部動態特性參數一直成為研究熱點。

滾珠絲杠進給單元主要存在兩種類型結合部，即螺栓聯結的固定結合部與滾珠絲杠副、滾動導軌副、軸承的滾動結合部。目前，對滾動結合部動態特性參數識別已有諸多研究，其方法有理論計算法、實驗測試法及理論計算與實驗測試結合方法三種。對滾珠絲杠副結合部動態特性參數識別，文獻[7]基于Timoshenko理論并考慮螺母內部絲杠彈性變形，建立滾珠絲杠結合部剛度計算模型；文獻[8]設計、制作滾珠絲杠結合部動態特性測試平臺，并實驗獲得軸向剛度及阻尼參數；文獻[9]通過準靜態分析與實驗結合方法識別滾珠絲杠結合部的動態剛度矩陣。對滾動導軌結合部動態特性參數識別，文獻[10]基于Hertz接觸原理及二維切比雪夫多項式擬合法，分別建立直線滾動導軌結合部動態特性參數模型、非參數模型；文獻[11]通過研制滾動導軌結合部動態特性參數測試裝置，實驗獲得結合部法向剛度及阻尼參數；文獻[12]通過線性動力學理論方程與實驗模態測試相結合方法識別直線伺服系統滾珠絲杠副、滾動導軌副等結合部剛度及阻尼參數。對軸承結合部動態特性參數識別，文獻[13]建立深溝球軸承改進的靜剛度及動態支承剛度數學模型；文獻[14]通過設計軸承測試裝置，實驗研究軸交角、軸承旋轉速度、溫度等因素對結合部剛度、阻尼參數的影響規律；文獻[15]通過子結構法理論建模與實驗相結合方法識別箔片空氣軸承的剛度及阻尼參數。

對裝配狀態下進給單元滾動結合部參數識別，因該參數受裝配預緊力、間隙、摩擦等條件影響較大，需在進給單元裝配完成后方可精確識別。以上研究中由于理論計算法計算過程復雜繁瑣且準確性較低，而實驗測試法只能識別出單個結合部的動態特性參數及理論計算與實驗測試相結合方法難以獲取裝配狀態下滾動導軌副、軸承等頻響函數，故精確識別裝配狀態下進給單元滾動結合部參數較困難。另外，由于絲杠具有長徑比大、剛性低等特點，絲杠截面振動情況沿軸向存在較大差異，若將絲杠簡化為剛體則會產生較大建模誤差。

為此，本文提出進給單元裝配狀態下滾動結合部軸向動態特性參數識別新方法。即在建模過程中考慮絲杠截面軸向振動差異，將絲杠簡化為彈性桿件以提高進給單元的建模精度，并在進給單元裝配完成后從整體結構中識別出滾動結合部的軸向動態特性參數。以自行研制的滾珠絲杠進給實驗臺為對象，用該方法對左、右端軸承組及滾珠絲杠副結合部的軸向剛度及阻尼參數進行識別，并實驗驗證結果的正確性。

1進給單元基本結構

數控機床滾珠絲杠進給單元典型結構見圖1，圖中1為伺服電機，2為聯軸器，3為左軸承座，4為左軸承組，5為導軌滑塊，6為絲杠螺母，7為螺母座，8為絲杠，9為工作臺，10為床身，11為右軸承組，12為右軸承座。交流伺服電機通過聯軸器帶動絲杠轉動，通過絲杠螺母副將旋轉運動轉化為直線運動，實現工作臺沿滾動導軌直線進給。絲杠兩端分別由左、右滾動軸承組支撐，左、右軸承座由螺栓緊固于床身。水平進給單元絲杠常用支撐方式為一端固定一端簡支，可有效釋放絲杠溫升引起的伸長量。為提高各滾動結合部支撐剛度、消除絲杠回程誤差，進給單元裝配時對絲杠螺母副、滾動導軌副及支撐軸承組預緊，并對絲杠進行預拉伸以減小絲杠徑向變形。

圖1　滾珠絲杠進給單元結構簡圖 Fig.1 Structure diagram of the ball screw feed drive unit

2動態特性參數識別模型

2.1絲杠軸向振動方程

為便于建立滾珠絲杠進給單元軸向振動方程，將左右兩端軸承座、工作臺、床身均簡化為剛體；相對于滾動結合部，軸承座-床身、導軌滑塊-工作臺、絲杠螺母-螺母座等栓接固定結合部剛度、阻尼較大可簡化為剛性連接；左、右端軸承組及滾珠絲杠副結合部簡化為軸向彈簧-阻尼單元，滾動導軌副軸向剛度、阻尼參數幾乎為零忽略不計；細長絲杠在軸向力作用下會產生較大彈性變形，絲杠軸向各點振動并不相同，因而不能簡化為剛體，本文將絲杠簡化為材料均勻、各向同性的等截面彈性桿件。據簡化條件建立進給單元軸向力學模型見圖2。

圖2　進給單元軸向力學模型 Fig.2 Axial mechanical model of the feed drive unit

進給單元左端軸承組、右端軸承組、滾珠絲杠副結合部軸向剛度及阻尼分別為kl、cl，kr、cr，ka、ca。左端軸承組、絲杠螺母及右端軸承組對絲杠的等效支撐點分別設為A、B、C,A與B、B與C之間距分別記為l1、l2。對質量為M的工作臺施加水平方向簡諧激振力F=F0eiwt(F0為幅值，w為角頻率)，則工作臺發生簡諧振動um=Umeiwt。工作臺通過絲杠螺母副帶動絲杠沿軸向作簡諧振動，設絲杠上任一點到A點的軸向距離為x，則A點到B點左側范圍內絲杠軸向振動偏微分方程為

(1)

式中：u(x,t)為絲杠上x點截面軸向振動位移，為距離x與時間t的二元函數；E，S，m分別為絲杠的彈性模量、橫截面積、線密度。

由于絲杠在簡諧力作用下發生受迫簡諧振動，而其軸向各點振幅不同，則u(x,t)可表示為

u(x,t)=U(x)eiwt

(2)

式中：U(x)為絲杠軸向振型函數。

將式(2)代入式(1)得

(3)

式(3)的通解可表示為

U(x)=UAf1(x)+UA′f2(x)

(4)

式中：UA為絲杠上A點截面軸向振動位移幅值；UA′為A點U(x)對x的一階導數。

A點截面所受軸向力幅值NA可表示為

(5)

因此，式(4)可表示為

(6)

A點截面邊界條件為

(7)

由式(3)～式(7)得

f1(x)=cos(ζx)

(8)

(9)

絲杠B點左側截面軸向振動位移及軸向力分別設為uBl=UBleiwt及nBl=NBleiwt，由式(6)得

(10)

ESUAf1′(l1)+NAf2′(l1)

(11)

式中：f1′(x)，f2′(x)分別為f1(x)，f2(x)導函數，即

f1′(x)=-ζsin(ζx)

(12)

f2′(x)=cos(ζx)

(13)

式(10)、(11)可表示為矩陣形式，即

(14)

式(14)記為

(15)

絲杠C點截面軸向振動位移及軸向力分別設為uC=UCeiwt及nC=NCeiwt，絲杠B點右側截面軸向振動位移及軸向力分別設為uBr=UBreiwt及nBr=NBreiwt。據式(14)同理可得UC，NC與UBr，NBr關系式為

(16)

式(16)記為

PC=T2PBr

(17)

絲杠B點左右兩側截面振動位移關系為

uBl=uBr=uB=UBeiwt

(18)

以絲杠B點左右兩側截面為分析對象，其軸向力學模型見圖3。

圖3　絲杠B點左右兩側截面軸向力學模型 Fig.3 Axial mechanical model of the screw sections at B point

B點截面軸向振動微分方程為

(19)

由式(19)得

NBl=NBr+(ka+iwca)(Um-UB)

(20)

由式(18)、(20)得絲杠B點右側截面軸向振動位移幅值UBr、軸向力幅值NBr與B點左側截面振動位移幅值UBl、軸向力幅值NBl關系為

(21)

2.2工作臺軸向振動方程

以工作臺為分析對象，其軸向力學模型見圖4。

圖4　工作臺軸向力學模型 Fig.4 Axial mechanical model of the workbench

工作臺軸向振動微分方程為

(22)

由式(22)得

(23)

以上基于軸向振動理論、桿理論及傳遞矩陣法建立進給單元的軸向線性動力學模型，由于進給單元的摩擦、間隙及陀螺效應等非線性因素導致的建模誤差較小，未予考慮。

2.3動態特性參數識別方程

將式(23)代入式(21)得

(24)

式(24)記為

PBr=T3PBl-Pf

(25)

聯立式(15)、(17)、(25)得

PC=T2T3T1PA-T2Pf

(26)

令

(27)

絲杠A點截面軸向振動微分方程為

(29)

由式(29)可得NA與UA關系為

NA=(kl+iwcl)UA

(30)

絲杠C截面軸向振動微分方程為

(31)

由式(31)得NC與UC關系為

NC=-(kr+iwcr)UC

(32)

聯立式(28)、(30)、(32)，以UA、UC為未知量，解二元一次方程組，得

(33)

式中：α，β表達式分別為

α=(ka+iwca)F0{ES[f2′(l2)T11-f2(l2)T21]+

(kl+iwcl)[f2′(l2)T12-f2(l2)T22]}

(34)

β=(ka+iwca-w2M){(ES)2T21+ES(kl+

iwcl)T22+(kr+iwcr)[EST11+(kl+iwcl)T12]}

選取2017年5月—2018年5月醫院收治的急性闌尾炎患者52例進行回顧性分析，患者表現為右下腹疼痛，伴有發熱、惡心、嘔吐等癥狀。所有患者均接受CT診斷，經手術病理確診。52例患者中包括男29例，女23例；年齡21～69歲，平均（39.4±5.2）歲；其中47例患者進行CT平掃，5例實施CT增強掃描檢查。

(35)

由式(2)對t求導得C點軸向振動速度幅值為

(36)

在式(34)～式(36)中，C點軸向振動速度幅值VC、激振力幅值F0、激振力角頻率w(w=2πf，f為激振頻率)、絲杠支撐點間距離l1、l2可由測試獲得，式(36)轉化為以參數kl、kr、ka、cl、cr、ca為未知量的方程，即

VC=λ(kl,kr,ka,cl,cr,ca)

(37)

若保持激振力頻率f不變，改變6次絲杠支撐點間距l1、l2，可由測試獲得6組數據{l1t,l2t,F0t,f,VCt,(t=1,2,3,4,5,6)}，將其代入式(37)可得關于kl、kr、ka、cl、cr、ca的六元一次方程組，即

VCt=λt(kl,kr,ka,cl,cr,ca),(t=1,2,3,4,5,6)

(38)

通過數學方法求解式(38)可獲得左、右端軸承組及滾珠絲杠副結合部的軸向剛度及阻尼參數。

3實驗研究

3.1實驗測試

以自行研制的滾珠絲杠進給實驗臺為研究對象，見圖5，絲杠左、右端分別由2對、1對NSK角接觸軸承支撐，基于本文方法對其左、右端軸承組及滾珠絲杠副結合部軸向動態特性參數進行識別。實驗測試原理見圖6，信號發生器輸出簡諧激勵信號，通過功率放大器驅動激振器作簡諧運動，激振器懸掛、固定于人字梯上對工作臺進行水平軸向激振；激振器激振桿端部安裝力傳感器，用數據采集設備將激振力信號采集至計算機；用激光測振儀測量絲杠右端截面軸向振動速度信號，并將數據保存至計算機；實驗時所用主要設備、型號見表1。

圖5　滾珠絲杠進給實驗臺外觀結構圖 Fig.5 External view of the ball screw feed drive table

圖6　實驗測試原理圖 Fig.6 Experimental test principle

表1　實驗設備及型號

圖7　實驗系統設置 Fig.7 Experiment system setup

表2　實驗數據

圖8　第一組實測激振力、振動速度信號 Fig.8 Exciting force and vibration velocity signal of group No.1

3.2軸向動態特性參數識別

工作臺與滾珠絲杠基本參數見表3。

表3　絲杠、工作臺基本參數

將表2、表3中數據代入式(38)，建立結合部軸向剛度、阻尼參數的識別方程組，即

(39)

式中：λ(kl,kr,ka,cl,cr,ca)為與l1，l2，F0，w，M，E，S等參數有關的函數。

分析式(39)可知，該方程組未知量較多且十分復雜，用傳統變量消元法、代入法等求解較困難。本文將該求解問題轉化為參數優化問題，用優化算法求解。

遺傳算法為高效并行的優化搜索算法[16]，模擬生物群體進化與自然選擇機制，通過選擇、交叉、變異的遺傳操作，能快速、準確找到相對某個問題的最優解。由于其具有收斂速度快、搜索準確性高及優化結果理想等優點被迅速推廣到路徑規劃、優化配置、參數識別[17-18]及復雜數學方程求解等。本文用遺傳算法求解方程組(39)。具體優化求解中的關鍵設置為：

(1)優化變量。以kl，kr，ka，cl，cr，ca為優化變量，并記為φ=[kl,kr,ka,cl,cr,ca]。

(2)目標函數。以絲杠C點截面軸向振動速度幅值的理論計算值與實驗測試值建立優化目標函數，即

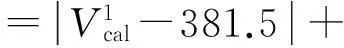
(40)

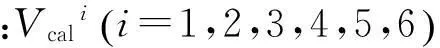
(3)染色體編碼方式。由于剛度、阻尼參數變化范圍較大，用二進制編碼方式會使遺傳算法不能兼顧編碼精度及計算效率要求。本文采用十進制浮點數對染色體進行編碼，一組剛度、阻尼參數構成一條染色體，每個基因位置對應一個待識別參數，編碼方式見圖9。

圖9染色體編碼方式
Fig.9 Chromosome encoding model

(4)適應度函數。該函數用于計算個體適應度值，值越大個體存活概率越大。據式(40)優化問題目標函數，個體目標函數值越小其適應度值越大。建立適應度函數為

(41)

(5)遺傳算子。選擇算子采用賭輪盤選擇方法，個體按與適應度成正比的概率向下一代群體繁殖；交叉算子采用單點交叉方法，對被選擇個體交叉操作；變異算子用均勻變異法，對個體進行變異操作。

(6)收斂準則。本文設置最大進化代數終止遺傳操作。

基于Sheffield遺傳算法工具箱函數并用MATLAB語言編制求解程序，基本流程見圖10。在遺傳算法優化求解過程中，最優解與種群均值變化見圖11。由圖11可知，遺傳算法在第154代已基本收斂，對應目標函數最小值為12.0 μm/s，識別所得結合部軸向剛度、阻尼參數見表4。

表4　軸向剛度、阻尼參數識別結果

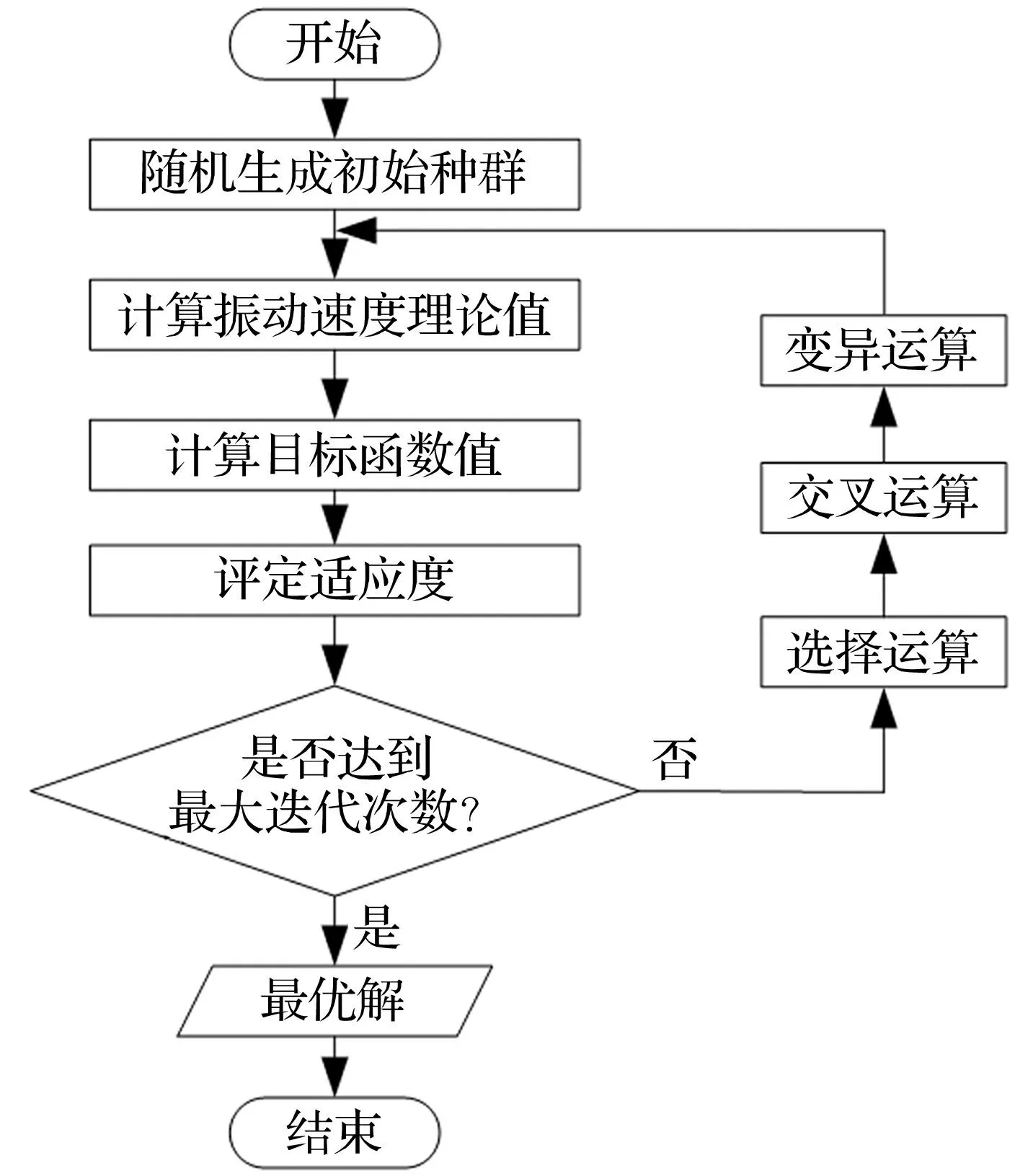
圖10　遺傳算法基本流程 Fig.10 Basic flow of genetic algorithm

圖11　最優解及種群均值變化 Fig.11 Change of optimal solution and population average

將識別所得結合部動態特性參數及實驗數據代入式(36)計算C點軸向振動速度的理論計算值Vcal，并與表2中實驗測試值Vtest比較，見表5。由表5可知，絲杠C點軸向振動速度的理論值與實驗值一致性較好，最大誤差為6.3 μm/s，方程組求解在誤差范圍內取得滿意結果。

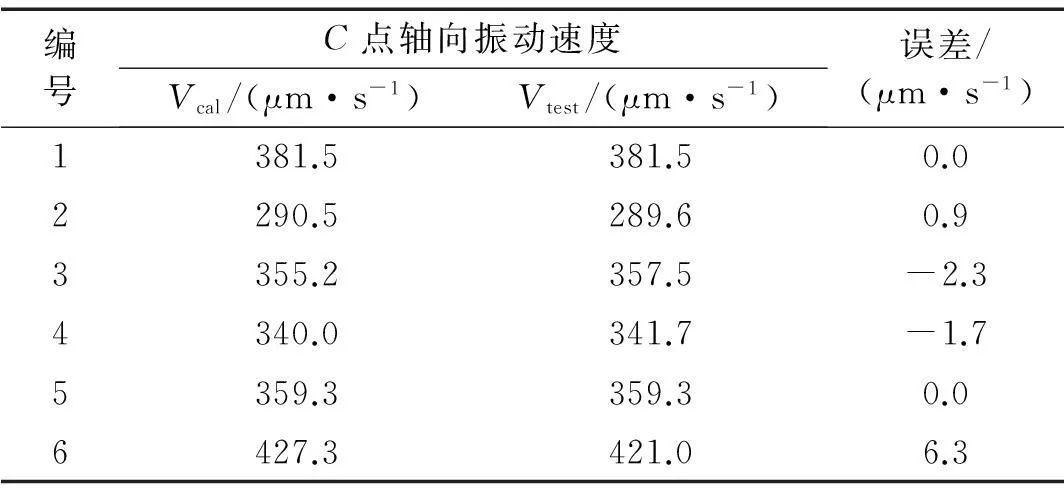
表5　C點軸向振動速度比較

3.3識別方法正確性驗證

表6　理論計算值與實驗測試值對比

4結論

(1)本文所提滾珠絲杠進給單元裝配狀態下其滾動結合部軸向動態特性參數識別方法，將絲杠簡化為彈性桿件以建立簡諧力作用下絲杠及工作臺的軸向振動方程，建立結合部軸向剛度、阻尼參數的識別模型；通過測量絲杠支撐點間距離、簡諧激振力頻率及幅值、絲杠軸端截面軸向振動速度幅值等參數建立識別方程組；基于遺傳算法優化求解方程組，識別出結合部的軸向剛度及阻尼參數。

(2)以自行研制的滾珠絲杠實驗臺為實驗對象，基于本文所提方法對其左、右端軸承組及滾珠絲杠結合部的軸向剛度與阻尼參數進行識別，并通過實驗對識別結果的正確性進行驗證。實驗結果表明本文方法正確、有效；絲杠軸端截面軸向振動速度幅值的理論計算值與實驗測試值絕對誤差在7.7 μm/s以內，識別精度較高。

(3)本文方法能在數控機床進給單元裝配完成后，準確識別出絲杠左、右端軸承組及滾珠絲杠副結合部的軸向剛度、阻尼參數，為數控機床進給單元的理論建模、動態特性優化及伺服控制系統設計提供準確的結合部參數，并為復雜機械系統結合部動態特性參數識別提供參考。

參考文獻

[1]董亮, 湯文成, 劉立. 滾珠絲杠進給系統混合建模及其振動時變性分析[J]. 振動與沖擊, 2013, 32(20): 196-202.

DONG Liang, TANG Wen-cheng, LIU Li. Hybrid modeling and time-varying analysis of vibration for a ball screw drive[J]. Journal of Vibration and Shock, 2013, 32(20): 196-202.

[2]AltintasY, Verl A, Brecher C, et al. Machine tool feed drives[J]. CIRP Annals-Manufacturing Technology,2011,60(2):779-796.

[3]Zhang G P, Huang Y M, Shi W H, et al. Predicting dynamic behaviours of a whole machine tool structure based on computer-aided engineering[J]. International Journal of Machine tools and Manufacture, 2003, 43(7): 699-706.

[4]Zhou Y, Peng F Y, Wang G X. A study on the dynamic characteristics of the drive at center of gravity (DCG) feed drives[J]. The International Journal of Advanced Manufacturing Technology, 2013, 66(1/2/3/4): 325-336.

[5]劉海濤,王磊,趙萬華. 考慮模態特性的高速機床進給系統剛度匹配研究[J]. 西安交通大學學報, 2014, 48(1): 90-95.

LIU Hai-tao, WANG Lei, ZHAO Wan-hua. Stiffness matching designing for feed system of high-speed machine tool considering modal characteristics[J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 90-95.

[6]王永強,張承瑞. 滾珠絲杠進給系統仿真建模[J]. 振動與沖擊, 2013, 32(3): 46-49.

WANG Yong-qiang, ZHANG Cheng-rui. Simulation modeling of a ball screw feed drive system[J]. Journal of Vibration and Shock, 2013, 32(3): 46-49.

[7]Okwudire C E. Improved screw-nut interface model for high-performance ball screw drives[J]. Journal of Mechanical Design, 2011, 133(4): 041009.1-041009.10.

[8]程序,史金飛,張思. 加工中心機床滾珠絲杠結合面的動態特性[J]. 中國機械工程, 1994, 5(1)：29-31.

CHENG Xu, SHI Jin-fei, ZHANG Si. A Study on dynamic characteristics of the joint surfaces of ball screw assembly[J]. China Mechanical Engineering, 1994, 5(1)：29-31.

[9]Chen Y J, Tang W C. Dynamic contact stiffness analysis of a double-nut ball screw based on a quasi-static method[J]. Mechanism and Machine Theory, 2014, 73: 76-90.

[10]Dhupia J S, Ulsoy A G, Katz R, et al. Experimental identification of the nonlinear parameters of an industrial translational guide for machine performance evaluation[J]. Journal of Vibration and Control, 2008, 14(5): 645-668.

[11]張華,袁軍堂,汪振華. 滾動導軌結合面動態特性參數識別實驗研究[J]. 中國機械工程,2011, 22(4): 415-418.

ZHANG Hua, YUAN Jun-tang, WANG Zhen-hua. Experimental research on identification of dynamic characteristic parameters of rolling guide’s joint[J]. China Mechanical Engineering, 2011, 22(4): 415-418.

[12]Yang T, Lin C S. Identifying the stiffness and damping parameters of a linear servomechanism[J]. Mechanics Based Design of Structures and Machines, 2004, 32 (3): 283-304.

[13]Dougdag M, Ouali M, Boucherit H, et al. An experimental testing of a simplified model of a ball bearing: stiffness calculation and defect simulation[J].Meccanica,2012,47(2):335-354.

[14]Jacobs W, Boonen R, Sas P, et al. The influence of the lubricant film on the stiffness and damping characteristics of a deep groove ball bearing[J]. Mechanical Systems and Signal Processing, 2014, 42(1/2): 335-350.

[15]Arora V, Hoogt P J M, Aarts R G K M, et al. Identification of stiffness and damping characteristics of axial air-foil bearings [J]. International Journal of Mechanics and Materials in Design, 2011, 7(3): 231-243.

[16]田莉,陳換過,祝俊,等. 基于自適應模擬退火遺傳算法的傳感器優化配置研究[J].振動工程學報, 2012, 25(3): 238-243.

TIAN Li, CHENG Huan-guo, ZHU Jun, et al. A study of optimal sensor placement based on the improved adaptive simulated annealing genetic algorithms[J]. Journal of Vibration Engineering, 2012, 25(3): 238-243.

[17]TasanA S, Gen M. A genetic algorithm based approach to vehicle routing problem with simultaneous pick-up and deliveries[J]. Computers & Industrial Engineering, 2012, 62 (3): 755-761.

[18]劉永強,楊紹普,廖英英,等. 基于遺傳算法的磁流變阻尼器Bouc-Wen模型參數辨識[J]. 振動與沖擊,2011,30(7):261-264.

LIU Yong-qiang, YANG Shao-pu, LIAO Ying-ying, et al. Parameter identification of Bouc-wen model for MR damper based on genetic algorithm[J]. Journal of Vibration and Shock, 2011, 30(7): 261-264.