壓縮感知的人臉圖像去噪
林克正++魏穎+程衛月


摘要:為解決人臉識別領域的噪聲圖像恢復問題,提出一種壓縮感知的人臉圖像去噪算法,協同稀疏性度量(collaborative sparse measure,CSM). CSM算法利用圖像的先驗知識,用一個域將圖像稀疏表示,將圖像的二維稀疏表示和三維稀疏表示同時進行自適應混合空間域轉換,利用增廣拉格朗日技術求解.實驗結果表明,CSM算法的信噪比明顯高于傳統算法的信噪比,具有高效性.
關鍵詞:壓縮感知;協同稀疏性度量;圖像去噪;空間域
DOI:10.15938/j.jhust,2015.05.018
中圖分類號:TP391.4
文獻標志碼:A
文章編號:1007-2683(2015)05-0091-06
0 引言
壓縮感知的基本思路是對數據進行變換后,完成從較少的數據中提取較多的信息,壓縮感知理論為傳統的信息處理打開了新的篇章.目前,在對圖像噪聲濾除方面,常用的算法有樹結構小波(tree-structured wavelet,TSW),樹形結構的離散余弦變換(tree-structured wavelet discrete cosine transform,TSWDCT),總度差(total variation,TV)等,它們能不同程度地濾除圖像噪聲,恢復圖像本身.針對高斯噪聲干擾人臉圖像這一問題,本文提出協同稀疏性度量(CSM)來對噪聲圖像進行恢復,該算法利用圖像的先驗知識,尋求一個基,并利用圖像的局部平滑特性和非局部自相似性質,其中二維稀疏表示利用到圖像的垂直梯度和水平梯度對圖像濾波,三維稀疏表示首先將贗本劃分成n個大小相等的塊,尋找最佳匹配塊進行三維轉換,最后用增廣拉格朗日技術求解,提高濾除圖像噪聲的能力,恢復圖像本身.
1 壓縮感知理論和增廣拉格朗日方法
1.1 壓縮感知理論
一個長度為Ⅳ的信號U在基ψ下是稀疏的,如果它的變換系數是零或接近于零,則稀疏的量化是通過系數向量里重要元素的個數來決定,具體地,給定M個線性測量,b個信號U的壓縮感知恢復問題是如式(1)約束的優化問題.
A表示隨機投影.P通常被設置成1或0,特征向量的稀疏性為 是l1范數,當 是l0范數時給向量加上絕對值,并且計算向量的非零元素.壓縮感知理論是能夠從b個樣本M中恢復出稀疏信號U,前提是隨機樣本的數量M≥aK.所需要的樣本采樣率為M/K,為了完全恢復樣本,比例應該為K/N.
1.2 增廣拉格朗日方法
式(2)為線性約束問題.增廣拉格朗日函數的定義為式(3).
2 基于壓縮感知的噪聲圖像恢復算法
2.1 算法的提出
該方法采用人臉圖像的兩種先驗知識,即自然圖像的局部平滑和非局部自相似性,而圖像的稀疏性能和自然圖像的兩個性能一致.
一個通用的稀疏性度量類型可被描述成通過壓縮感知恢復的高保真圖像,稱作協同稀疏性度量.建立一個自適應數據混合空間變換域,這個域合并另外兩個互補的稀疏的局部二維域 和非局部三維稀疏域 .
P和Q通常被設置在[0,1]之間,a是一個正規化參數,ψL2D對應于上述的先驗知識局部平滑,保持圖像的局部一致性,有效地抑制噪聲,ψN3D對應于上述的先驗知識局部自相似性,保持圖像非局部一致性,同時保持銳利且邊緣有效.
2.2 特征設計
2.2.1 空間域的局部二維特征
對于自然圖像,首選響應盡可能小的一組濾波器,因為濾波后的圖像和高通濾波器的一些卷積是稀疏的,大多數像素強度接近零,這種類型的稀疏性為空間域的局部二維稀疏.
實踐中廣泛使用的濾波器是水平和垂直的差分算子,用Dv和Dh表示,這分別對應于垂直梯度和水平梯度的圖片,不失一般性,梯度圖像是由廣義高斯分布模擬.令 ,另p在式(4)中實現空間域ψL2D的局部二維稀疏,如式(5).
對于各項異性的總變化,ψL2D。具有相同的表達式.在本文中,ψL2D經常被用來描述自然圖像的局部平滑,ψL2D也可以取代二階導數或更復雜的學習過濾器,p被設置成1/2或1/3的超拉普拉斯先驗知識.
2.2.2 非局部的三維稀疏變換域
非局部的自相似性體現一些稀疏度量的屬性,借助于系數的稀疏性和整合來重塑自相似性,取得通過堆疊相似圖像的斑點轉化產生的3D組,這種稀疏性為非局部的三維稀疏變換域,
如圖1所示,對于每個塊,找到在一個搜索窗口相抵的塊,那些塊被堆積在一個3D的數組內.為獲得系數,在一個3D數組內進行3D轉換,用非零系數的數目來衡量這個斑點的非局部3D稀疏性,通過整合所有塊來取得整幅圖像的非局部3D稀疏性,
逆算子AN3D的定義為:在獲取ΦX以后,將它分割為n組3D變換系數,然后再逆序產生每一塊的估計值,用每一塊的估計值返回到它們的原始的位置,最終的圖像估計值為所有塊的平均值估計,其中,X的估計值為 .
2.3 協同的稀疏測量
非局部的三維稀疏利用自然圖像的自相似性,借助于稀疏系數來表示自然圖像的自相似性特征,并由轉化3D組產生的堆疊相似圖像塊獲得.稀疏性不僅能夠保留自相似塊中的紋理特征,也能在一定程度上保持不同塊中的不同特征.因此,提出用協同稀疏性度量來解決噪聲圖像的恢復問題.
考慮到整體的局部平滑性和非局部自相似性,CSM在空間域局部2D稀疏性和變換域非局部3D稀疏性的表示如式(7).利用稀疏的高度性,將自然圖像映射到高維自適應混合空間變換域,限制了CSM的解空間.
3 實驗結果與分析
實驗采用的人臉圖像為兩張灰度圖像和一幅自然圖像,用matlab2010進行測試.每個塊的大小BS設置為8x8,待測窗口搜索塊的大小設置為41×41,經驗值為1,μ=28,0=2,,本文中β=32或盧= 64,τ=8或τ=12.
3.1 濾除圖像噪聲實驗
用樹結構小波算法,樹形結構的離散余弦變換算法和總度差與本文方法作比較,用圖像的信噪比(signal-to-noise ratio,SNR)表現結果,信噪比的單位用dB表示.
將圖3中受高斯噪聲干擾的人臉圖像用4種方法進行恢復,其中,圖3中的3幅人臉圖像受到了同樣的高斯噪聲干擾.圖4、圖5、圖6分別為TSW算法、TSWDCT算法、TV算法和本文算法對圖像去噪后的效果,從左到右顯示序號分別為算法1、2、3和4,可看到本文算法的恢復效果最好.
表1展示了4種方法在不同情況下的信噪比,由表1可以看出,本文方法的平均信噪比比TSW算法平均高8.49dB,比TSWDCT算法平均高5.23dB,比TV算法平均高的3.49dB,所以本文方法有很好的濾除圖像噪聲來恢復圖像的能力,
每種算法對不同樣本取得的平均信噪比結果如圖7所示,看到本文算法的最高信噪比可達到接近34dB,比TV算法的接近31dB高出3dB,跟TSW和TSDCT兩種算法比較高出的更多,足以說明本文方法的高效性.
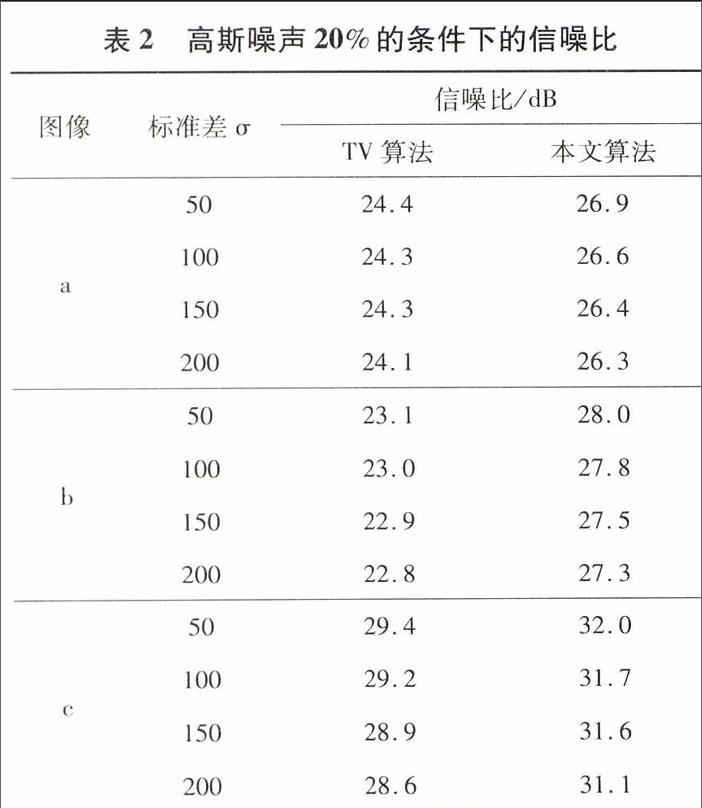
表2和3顯示了3幅圖片的高斯噪聲在20%和30%的情況下,并且標準差σ從50到200不等的情況下的信噪比結果,由于TV算法和本文算法對高斯噪聲都是穩定的,所以對這兩種算法做比較,從表2和表3可看出,本文算法對圖像噪聲的濾除能力明顯高于TV算法,
表4顯示了兩種算法在上述情況下的執行時間,本文算法的執行時間是TV算法的執行時間的兩倍左右,這是因為本文算法的復雜度高造成的.
圖8描繪了不同比率下測量圖像的信噪比與迭代次數的關系.迭代次數增加,圖像重建的信噪比快速增加并趨于穩定.從圖8曲線看出圖像不光滑,迭代過程中有尖點,導致這種情況原因有二,一是原函數具有凸性,另一原因是本文算法避免收斂于局部最優解而試圖實現全局最優解
4 結語
本文提出了一種壓縮感知的人臉圖像去噪算法,該算法以壓縮感知理論為基礎,引入協同稀疏性度量,一方面,有效地刻畫自然圖像中固有的稀疏自適應空間變換域;另一方面,該算法對高斯噪聲穩定,更有利于濾除圖像噪聲,恢復圖像本身.該算法與其他算法相比,濾除圖像噪聲能力強,且壓縮感知理論在濾除圖像噪聲中頗具潛力.

