溫度-離心-振動復合響應分析大規模并行程序設計

牛紅攀　肖世富　范宣華

(中國工程物理研究院總體工程研究所　四川綿陽　621999)

?

溫度-離心-振動復合響應分析大規模并行程序設計

牛紅攀肖世富范宣華

(中國工程物理研究院總體工程研究所四川綿陽621999)

摘要：再入空間階段的飛行器受氣動加熱、過載、流致振動等影響，結構的動力學響應復雜。針對溫度、離心載荷對結構振動響應的影響，介紹了溫度-離心-振動復合響應分析基本理論，基于PANDA平臺設計并實現了大規模并行程序，通過算例驗證了程序的正確性。溫度-離心-振動復合響應分析技術研究及程序設計工作將為武器系統再入復合環境振動響應分析起到支撐作用，同時為其他領域的多場耦合分析提供借鑒意義。

關鍵詞：PANDA并行分析熱力耦合復合響應

戰略武器、航天飛機、彈道導彈、返回式衛星等再入空間階段的飛行器，受氣動加熱、過載、流致振動的影響，結構的動力學響應復雜。本文將研究結構熱應力、離心載荷與振動響應之間的耦合作用，分析溫度、離心運動對結構振動響應的影響，研發復合響應分析大規模并行程序，這對于保證飛行器等結構的安全性、可靠性具有重要意義。

溫度-離心-振動復合響應分析，本質上是熱應力、離心力作用下的剛柔耦合動力學。剛柔耦合系統動力學是多剛體系統動力學的自然延伸，它的各構件之間一般有較大的相對位移運動，而且在運動中要考慮構件的柔性，這使得系統運動的自由度、各構件相互之間的運動學及動力學關系復雜化。在溫度場未知的情況下，需要對熱傳導方程和動力學方程耦合分析。基于線彈性模型，JOHNSTON研究了在溫度時變規律已知的情況下太陽能帆板的剛-柔耦合動力學特性[1]。OGUAMANAM研究了中心剛體-薄板的剛-柔耦合特性，基于非線性理論，建立了熱流作用下的剛柔耦合系統的動力學模型，并對運動過程中的非線性效應進行研究[2]。李琳等研究了在溫度已知的情況下，閉環柔性多體系統的動力學性態，指出熱效應會引起各部件加速度和約束力的高頻振蕩[3]。劉錦陽等基于幾何非線性理論，研究了溫度場中柔性梁、板系統的動力學問題[4-8]。自2006年起，為提升大規模計算能力，中國工程物理研究院組織研發了PANDA平臺。PANDA平臺是一個面向實際復雜工程的多物理、大規模并行計算的CAE應用程序基礎平臺，采用了面向對象的、層次化的、模塊化的設計模式[9-17]。為了進一步快速研發大規模結構分析并行程序，從2013年開始，PANDA平臺基于JAUMIN框架進行了重構，設計并實現了功能高度可擴充的程序架構，根據模型與算法分離、算法與數據分離的原則，采用算法模塊化、模塊構件化的開發模式，構建必須的單元庫、材料庫、載荷庫及求解流程庫，程序已具有靜力、模態、振動響應分析功能，可實現上億自由度規模的并行計算[18-19]。本文針對飛行器、旋轉機構分析需求，將在已有功能基礎之上，設計并實現溫度-離心-振動復合響應分析功能。

1理論基礎

1.1穩態熱傳導分析

熱傳導可以定義為完全接觸的兩個物體之間或一個物體的不同部分之間由于溫度梯度而引起的內能的交換。穩態熱分析的熱傳導方程為橢圓型方程，對于三維直角坐標系，穩態熱傳導微分方程如下：

(1)

式中，T為溫度變量，k為溫度傳導系數，f為源項。

根據有限元理論進一步推導出矩陣形式描述的有限元格式：

[K]{T}={Q}

(2)

其中[K]為熱傳導矩陣，包含各單元對熱傳導矩陣的貢獻及第三類熱交換邊界條件對熱傳導矩陣的修正，即剛度矩陣，具有大型、對稱、稀疏、帶狀分布以及正定、主元占優的特點；{T}為節點溫度向量，{Q}為溫度載荷向量，包含熱流、熱交換以及熱源引起的溫度載荷。

1.2熱應力分析

溫度改變時，物體由于外在約束以及內部各部分之間的相互約束，使其不能完全自由脹縮而產生的應力，即熱應力。求解熱應力，既要確定溫度場，又要確定位移、應變和應力場，實際上是熱和應力兩個物理場之間的相互作用，故屬于耦合場分析問題。與其他耦合場的分析方法類似，根據耦合方式的不同，存在兩種方法：弱耦合和強耦合。弱耦合是先進行熱分析，然后將求得的節點溫度作為體載荷施加到結構應力分析中；強耦合則是指直接采用具有溫度和位移自由度的耦合單元，同時得到熱分析和結構應力分析結果。本文采用熱力弱耦合分析，求解步驟為：首先由熱傳導方程和邊界條件求出溫度分布，再由熱彈性力學方程求出位移和應力。

線性熱彈性問題的有限元格式為：

[K]{u}={Pf}+{Pth}

(3)

式中，[K]為整體剛度矩陣，{u}節點位移向量；{Pf}為結構載荷引起的節點載荷向量；{Pth}為溫度應變引起的節點載荷向量。其中

(4)

(5)

{εth}=α(T-T0)[1 1 1 0 0 0]T

(6)

其中[B]為幾何矩陣，[D]為彈性矩陣，{εth}為節點溫度應變向量，α為熱膨脹系數，T0為節點參考溫度，T為節點溫度。

熱應力可由如下公式計算得到：

[σ]=[D]([B]{u}-{εth})

(7)

從上述線性熱彈性問題的有限元計算公式中可以看出與線彈性問題有限元求解方程的區別是載荷向量中包括由溫度應變引起的溫度載荷{Pth}以及在計算應力時包含溫度應變引起的初應變項{εth}。當結構的溫度場已經求得時，帶入上述表達式即可進一步求出結構的位移、應變及應力。

1.3結構動力學特性分析

考慮熱應力、旋轉軟化效應和動力剛化效應，結構的動力學控制方程為

[Kc]+[Ks]){u}={F}

(8)

式中[M]為質量矩陣，[C]為阻尼矩陣，[K]為傳統剛度矩陣，[Kc]為旋轉軟化效應矩陣，[Ks]為應力剛化矩陣，包括熱應力和載荷的影響，{F}為外力向量，{u}為位移向量。

1.3.1旋轉軟化效應

在動力學分析時，旋轉結構與其他結構相比有一個很大不同：旋轉軟化效應。對于每個節點均有3個自由度的空間結構，在節點上旋轉軟化效應矩陣可表示為

(9)

式中：[M]為3×3的質量矩陣，ωx為繞X軸的角速度，ωy為繞Y軸的角速度，ωz為繞Z軸的角速度。

1.3.2應力剛化效應

當彈性體受到較大的外力將引起較大的變形時，采用線性化的應變與位移關系不能真實的反應彈性體的應變和應力狀態，忽略這種幾何非線性的影響直接導致了對彈性體的剛度估計偏低。考慮幾何非線性的影響可得出單元剛度矩陣為：

=[K0]e+[S]e

(10)

公式(10)中第一項即傳統的剛度矩陣，第二項為應力剛化矩陣。應力剛化矩陣[S]e可表示為：

(11)

式中[S0]為應力剛化子矩陣，表達式為

(12)

其中[Sm]為柯西應力，[G]為形函數的梯度。

2程序設計

2.1軟件總體架構

采用“基于框架開發應用軟件”的現代軟件開發理念，基于JAUMIN框架，在程序設計時首先考慮并行，根據模型與算法分離、算法與數據分離的原則，從偏微分方程弱形式出發，構建必須的單元庫、材料庫、載荷庫、計算流程庫。軟件的整體層次結構如圖 1所示，包括應用支撐層、有限元共性層、有限元個性層與應用服務平臺。其中應用支撐層主要為軟件提供數據支撐服務，包括JAUMIN變量的注冊、管理與使用、模型節點與模型單元數據管理、自由度映射表建立與管理、數值輸出以及對稱矩陣等常見工具箱；有限元共性層提煉了靜力與振動響應分析軟件的有限元計算共性部分，包括單元、材料、場數據、約束、載荷、求解流程等；有限元個性層針對不同的結構分析建立個性分析模塊，如針對結構應力分析，需要建立結構應力單元、結構材料、結構應力場、節點位移約束、節點力、壓力、重力、靜力求解流程、模態求解流程等；應用服務平臺即在此基礎之上建立專業領域的數值仿真平臺，同時具有二次開發功能等。

PANDA靜力與振動分析軟件的主要模塊如圖2所示，包括單元模塊、材料模塊、場模塊、約束模塊、載荷模塊、求解流程模塊等，其中FEManager為有限元方法接口，管理各個模塊，通過對各模塊的管理實現有限元方法的計算。

圖2　PANDA-STAVIB軟件主要模塊及模塊關系

2.2熱力弱耦合設計

弱耦合分析，即各物理場單獨分析，通過數據交互實現耦合。軟件初步實現了相同Patch下的弱耦合分析，即各物理場采用同樣的網格拓撲。各物理場單獨進行求解，通過場進行數據交互，多步迭代之后，可得到各物理場的解，如圖 3所示。對于熱力弱耦合分析，首先求解熱擴散方程得到溫度場的分析，之后根據熱彈性方程計算得到結構的熱應力和變形。

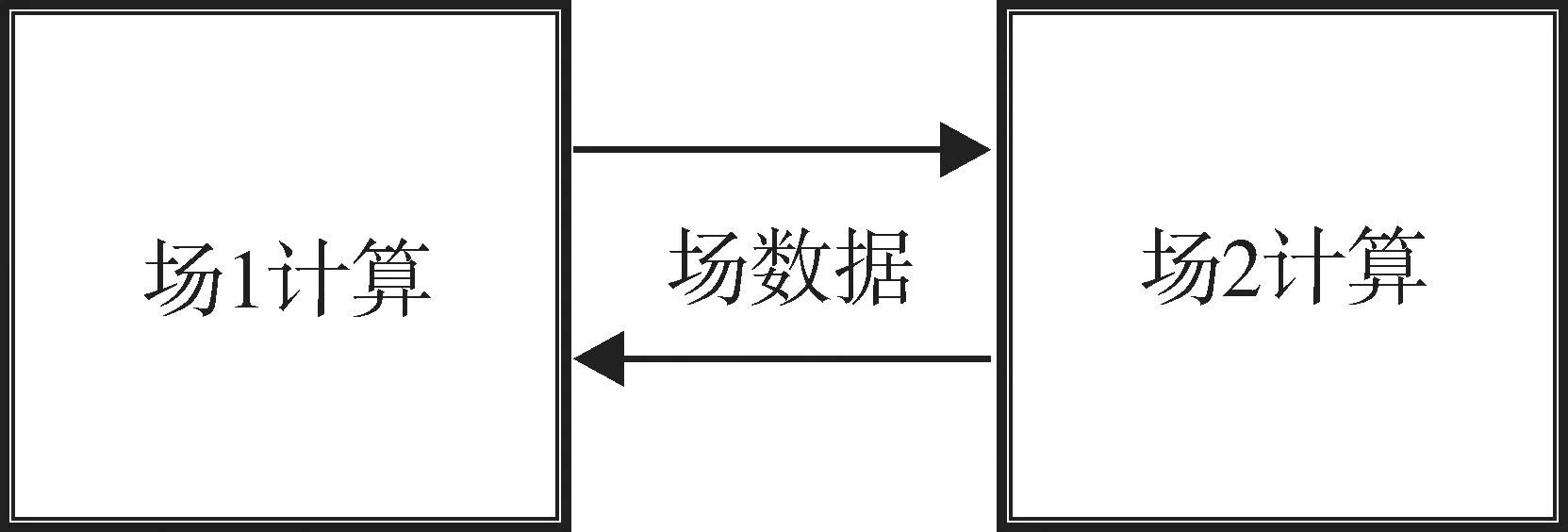
圖3　弱耦合分析示意圖

2.3序貫分析設計

軟件采用了多求解步設計實現序貫分析，每個求解步即單獨的一個分析類型，可執行一個完整的求解流程，數據均保存在場中，各求解步均可存取場中的數據。如圖 4所示，溫度-離心復合振動響應分析時，結構應力、溫度等數據均保存在場中，首先熱力分析計算得到熱應力分布，在模態分析時考慮熱應力帶來的預應力影響，之后根據模態分析的結果采用模態疊加法進行振動響應分析。

圖4　溫度-離心復合振動響應分析示意圖

3算例測試

算例所采用的模型為梁結構，材料參數如表 1所示。梁結構的尺寸為1 m×1 m×10 m。采用六面體單元進行網格劃分，六面體單元的邊長為1，整個模型節點數為44，單元數為10，如圖5所示。施加邊界條件為繞端部進行旋轉，旋轉角速度為100 rad/s，繞軸旋轉端的溫度為100 ℃，自由端溫度為20 ℃。

表1　算例采用材料的材料參數

圖5　算例模型網格示意圖

采用線性分析，模態計算結果如表 2所示，從表中數據對比可以看到PANDA的計算結果與ANSYS基本一致，驗證了包含動力剛化效應模態算法的正確性。

表2　算例模態分析結果

在坐標(0，0，10)處施加Y方向振幅為1e6 N的簡諧力，響應點坐標為(0，1，10)，阻尼比取0.01，利用PANDA程序計算的靜止狀態下的諧響應曲線與溫度-旋轉狀態相比如圖 6所示，可看到溫度-離心-振動耦合無論在固有頻率上，還是在振幅上均有不同，說明了熱應力、離心力對振動響應的影響。

圖6　不同狀態下的諧響應曲線對比

采用同樣的計算參數，分別利用PANDA和ANSYS計算了響應點處的諧響應，計算結果如圖7所示，從圖7可看到熱應力、離心力下的PANDA計算的諧響應曲線與ANSYS一致，驗證了PANDA溫度-離心-振動復合響應分析的正確性。

圖7　PANDA與ANSYS計算結果對比

4結論

本文研究了溫度-離心-振動復合響應分析算法，分析了熱應力、旋轉軟化效應和動力剛化效應，建立了考慮熱應力的旋轉結構控制微分方程，基于PANDA平臺進行了程序設計和代碼實現，最后設計了溫度-離心-振動復合響應分析算例驗證了程序的正確性。本工作將為武器系統再入復合環境振動響應分析起到支撐作用，同時為其他領域的多場耦合分析提供借鑒意義。

參考文獻

[1]JOHNSTON J D, THORNTON E A. Thermally induced attitude dynamics of a spacecraft with a flexible appendage [J]. Journal of Guidance, Control, and Dynamics, 1998, 21(4): 581-587.

[2]OGUAMANAM D, HANSEN J, HEPPLER G. Nonlinear transient response of thermally loaded laminated panels[J]. Journal of Applied Mechanics, 2004, 71(1): 49-56.

[3]李琳, 劉錦陽. 計及熱效應的閉環柔性機械系統的動力學分析 [J]. 機械科學與技術, 2006, 24(12): 1491-1494.

[4]劉錦陽, 崔麟. 熱載荷作用下大變形柔性梁剛柔耦合動力學分析 [J]. 振動工程學報, 2009, 22(1): 48-53.

[5]劉錦陽, 洪嘉振. 溫度場中的柔性梁系統動力學建模[J]. 振動工程學報, 2007, 19(4): 469-474.

[6]劉錦陽, 李彬, 陸皓. 計及熱應變的空間曲梁的剛-柔耦合動力學 [J]. 固體力學學報, 2007, 28(1): 30-36.

[7]劉錦陽, 袁瑞, 洪嘉振. 考慮幾何非線性和熱效應的剛-柔耦合動力學 [J]. 固體力學學報, 2008, 29(1): 73-77.

[8]劉錦陽, 袁瑞, 洪嘉振. 考慮熱效應的柔性板的剛-柔耦合動力學特性 [J]. 上海交通大學學報, 2008, 42(8): 1226-1232.

[9]FAN X H, WU R A, CHEN P. Scalability study on large-scale parallel finite element computing in Panda frame[J]. Applied Mechanics and Materials, 2012, 117:489-492.

[10] 陳成軍, 柳陽, 張元章, 等. 基于 PANDA 的并行顯式有限元程序開發 [J]. 計算力學學報, 2011, 28(B04): 204-207.

[11] 嵇曉宇, 郝志明, 莫軍, 等. 面向對象有限元并行計算框架 PANDA 求解器的服務構件化設計與集成 [J]. 計算機輔助工程, 2011, 20(1): 9-14.

[12] 李健, 郝志明, 寧佐貴. 基于 PANDA 框架的并行有限元模態分析程序開發和應用 [J]. 計算機輔助工程, 2011, 20(1): 29-32.

[13] 史光梅, 何穎波, 吳瑞安, 等. 面向對象有限元并行計算框架 PANDA 研究進展[A].見：proceedings of the 中國計算力學大會’2010 (CCCM2010) 暨第八屆南方計算力學學術會議 (SCCM8) 論文集[C]. 2010.

[14] 史光梅, 何穎波, 吳瑞安,等. 面向對象有限元并行計算框架 PANDA [J]. 計算機輔助工程, 2010, 19(4): 8-14.

[15] 孫樂, 何穎波, 吳瑞安,等. 面向對象有限元并行計算框架 PANDA 的多物理場耦合服務 [J]. 計算機輔助工程, 2011, 20(1): 19-23.

[16] 孫樂, 莫軍, 肖世富, 等. 復雜結構黏彈性問題的大規模并行計算研究 [J]. 應用數學和力學, 2014, (S1): 226-231.

[17] 徐建國, 石正軍, 郝志明,等. 基于 PANDA 框架的非線性靜力學有限元并行計算程序設計和初步驗證[J]. 固體力學學報, 2010, (S1): 294-298.

[18] FAN X, WANG K, XIAO S, et al. Some Progress on Parallel Modal and Vibration Analysis Using the JAUMIN Framework [J]. Mathematical Problems in Engineering, 2014.

[19] 孫運見, 孫樂. 基于 Jaumin 的等參單元算法框架設計[J]. 計算機輔助工程, 2015,(1):63-67.

E-mail:402niuhp@caep.cn

Massively Paralleled Program Design of Thermal-Centrifugal-Vibration

Composite Response Analysis

NIU Hong-pan, XIAO Shi-fu, FAN Xuan-hua

(InstituteofSystemsEngineering,CAEP,Mianyang621999,Sichuan,China)

Abstract:The dynamic response of the space vehicles, which in reentry space phase, is complicated with the effects of aerodynamic heating, overload, flow induced vibration, and so on. This paper focuses on the vibration response with thermal and centrifugal loads effects. Firstly, the basic theory of Thermal-Centrifugal-Vibration response is introduced. Massive paralleled program based on PANDA platform is designed and implementation. Finally a test is designed to verify the program correctness. Thermal-Centrifugal-Vibration composite response analysis paralleled program plays a support role in space vehicles in reentry space phase, as well provides reference for other multi-field coupling analysis.

Key words:PANDA; Paralleled simulation; Program design; Thermal-solid coupling

中圖分類號：O313.7；TP391

文獻標志碼：A

文章編號：1671-8755(2015)04-0042-05

作者簡介:牛紅攀(1981—)，男，博士，高級工程師，研究方向為復雜系統結構力學大規模并行計算、柔性多體動力學。

基金項目:國家自然科學基金青年基金(11402244)。