對稱非經典阻尼系統動力響應精確解算法比較

張　淼，　于　瀾

(長春工程學院 理學院， 吉林 長春　130012)

?

對稱非經典阻尼系統動力響應精確解算法比較

張淼，于瀾

(長春工程學院 理學院， 吉林 長春130012)

摘要：分別采用頻響函數法和復頻率響應法對同一個數值算例進行了穩態響應、使用條件和范圍以及誤差來源分析，闡述了兩種算法在工程執行過程中的特點及效率。

關鍵詞：非經典阻尼系統； 動力響應； 頻響函數矩陣； 標號現象

0引言

振型迭加法是動力分析中一種成熟且得到廣泛應用的方法，尤其是對那些振型關于阻尼矩陣具有正交性的系統十分有效，這種系統稱為經典阻尼系統，而當振型迭加法推廣至非經典阻尼系統時，其計算響應的過程相當復雜[1]。但如果將在N維空間中描述的非經典阻尼系統轉入2N維狀態空間中描述，利用復模態構造狀態向量，使用狀態向量對角化狀態矩陣來實現狀態方程的解耦[2]，再把得到的響應解返至N維空間中，求得用復模態參數表達的非經典阻尼系統的響應解(解析解)的算法，一般稱為復模態法或復頻率響應法[3]。當然這種算法也可用于求解經典阻尼系統，但需使用實模態參數表達[4]。近年來，又有文獻[5]提出了基于頻響函數計算經典和非經典阻尼系統精確解的新方法，與振型迭加法只能求解經典阻尼系統、復頻率響應法用實模態參數求解經典阻尼系統而用復模態參數求解非經典阻尼系統不同的是，這種新方法無論求解哪種阻尼系統的響應均使用的是實模態參數。

文中針對非經典阻尼動力系統，應用目前文獻中已經出現的求解振動系統響應的解析解的兩種算法進行詳細分析和算例比較，來說明它們在編程實現過程中的使用條件、使用范圍、誤差來源和計算效率等，并指出利用模態參數求解響應的過程中可能出現的標號現象、重頻現象及規范化常數的異常現象等。

1實模態參數與復模態參數

描述自由度為N的線性阻尼離散系統的自由振動方程為

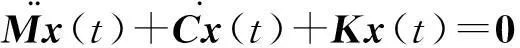
(1)

相應地其強迫振動方程為

(2)

式中:M∈RN×N----對稱系統的質量矩陣;

C∈RN×N----對稱系統的阻尼矩陣;

K∈RN×N----對稱系統的剛度矩陣。

結構有限元分析時，作拉普拉斯變換x(t)=uewt=uejωt代入式(1)可得

(w2Mu+wCu+Ku)ewt=0

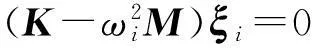
設每個實模態的正則化系數為ai，即

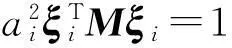
?i=1,2,…,N

記aiξi=vi，稱為無阻尼正則固有振型，簡稱為振型，則V=[v1,v2，…,vN]為振型矩陣，那么此時模態質量和模態剛度矩陣分別為

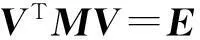
(3)

VTKV=diag(k1,k2，…,kn)=

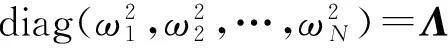
(4)

對經典阻尼系統有

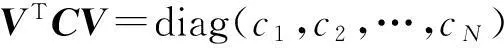
(5)

即模態阻尼矩陣為對角陣，其中阻尼比為

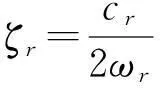
r=1,2,…,N

上面式(3)和式(4)為無阻尼正交條件，應用時有兩個問題要注意，一個是要注意標號現象的出現，例如按式(3)所示，應該有

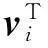
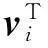
i≠j;i,j=1,2,…,N

但很多應用中，會出現例如下式

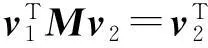
而

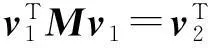
的現象發生，稱為標號現象[6]。一旦發現標號現象，要注意調整振型矩陣的標號次序，使式(3)成立。另一個問題是，一般情況下只要是單頻結構系統，即系統的固有頻率全不相同，那么式(3)就自動滿足，但當系統雖為重頻系統，也存在式(3)時，那么此重頻系統的響應求解也可按文中提及的算法來實現，相當于擴大了文中算法的使用范圍。

考慮阻尼時的系統極點及復模態對(λi,ui)(i=1,2,…,2N)滿足方程

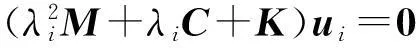
對于N自由度振動系統，特征方程det[λ2M+λC+K]=0有2N個呈復共軛對出現的特征值λ1,λ2,…,λ2N(其中λi+1為λi的共軛(i=1,3,…,2N-1))，稱為系統的極點。這些頻率對應著一組呈復共軛對出現特征向量ui∈CN稱為系統(1)與λi相對應的第i個模態向量。將u1,u2,…,u2N(其中ui+1為ui的共軛(i=1,3,…,2N-1))稱為復模態。它們的正交條件的形式有很多[7]，文中采用如下形式

對于N自由度振動系統，特征方程det[λ2M+λC+K]=0有2N個呈復共軛對出現的特征值λ1,λ2,…,λ2N(其中λi+1為λi的共軛(i=1,3,…,2N-1))，稱為系統的極點。這些頻率對應著一組呈復共軛對出現特征向量ui∈CN稱為系統(1)與λi相對應的第i個模態向量。將u1,u2,…,u2N(其中ui+1為ui的共軛(i=1,3,…,2N-1))稱為復模態。它們的正交條件的形式有很多[7]，文中采用如下形式

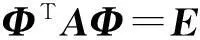
(6)

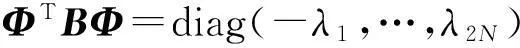
(7)

其中狀態向量矩陣為Φ=[φ1,φ2,…,φ2N]，狀態向量為φi=[uiλiui]T(i=1,2,…,2N)，且

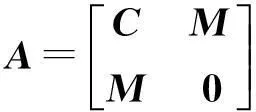
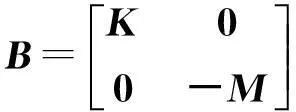
需要說明的是，復模態參數的標號現象可能更為常見，也如前文所述的方法加以處理，即可實現正交式(6)和式(7)，使標號現象并不致妨礙算法的應用。

2非經典阻尼系統動力響應的精確算法比較

當式(5)不能成立，即模態阻尼矩陣VTCV為非對角矩陣，那么系統為非經典阻尼系統。當然，對非經典阻尼系統不能再使用振型迭加法，目前文獻[5]中提出了基于頻響函數求解非經典阻尼系統的響應的方法。

2.1　基于頻響函數法

對振動系統式(2)，取激勵為簡諧激勵，f=[F1,F2,…,FN]Tsinωt，則

(8)

其中

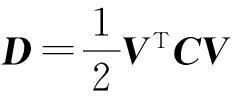
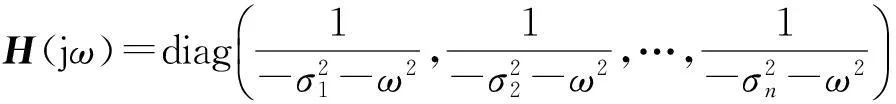
(9)

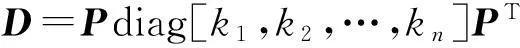
(10)

根據矩陣代數理論，矩陣函數

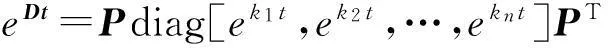
(11)

2.2　復頻率響應

對振動系統式(2)，取激勵為f=Fejωt，F=(F1,F2,…,FN)T，其復頻率響應為

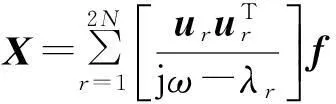
(12)

其復數解Xejωt中取虛部即為對應于簡諧激勵f=Fsinωt的響應解，這里λi,ui為復模態參數，u1,u2,…,uN為滿足正交性條件式(6)的規范化復模態。

3數值算例

文中考慮文獻[8]中給出的一個5自由度的質量彈性阻尼系統,此時

圖1　響應的擬合曲線

接下來以第1自由度為例，用復頻率響應算法(式(12))來計算響應，并與基于頻響函數計算的響應值進行比較，如圖2所示。

圖2　兩種算法計算的第1自由度響應值的對比圖

基于頻響函數求解非經典阻尼系統的響應方法與N-mark法同時計算系統響應時的比較結果，請參見文獻[5]。由文中的數值計算過程及結果可知：

1)復頻率響應法與基于頻響函數法在理論上都是計算非經典阻尼系統響應的精確算法。

2)但在用復頻率響應公式編程計算時，因為使用的是復模態參數，所以出現的標號現象較為嚴重，且當系統自由度較多時，不僅在調整標號來實現正交條件式(6)時遇到很大困難，而且規范化常數為復數，規范化后ΦTAΦ為近似單位陣，效果并不理想，導致復頻率響應計算結果出現較大偏差。而基于頻響函數法計算響應的算法在實現過程中，由于使用的是實模態參數，即使出現標號現象，調整標號的工作量也縮小了一倍，而且規范化常數為實數，規范化效果十分精確，體現其良好的工程應用性和計算效率。

4結語

在實際應用中，振型迭加法和相關的里茲向量法，以及直接積分法等各種方法可以組合使用來求解非經典阻尼系統，但多數情況下只能得到數值解。事實上為了更好地理解結構行為，用于諧波分析和響應譜分析，或許無論如何都要計算固有頻率和振型，這時由文中的分析可知，基于頻響函數的計算響應算法就會體現出良好的操作適應性，尤其可貴的是它得到的是響應的精確解。

參考文獻：

[1]Greco A， Santini A. Comparative study on dynamic analysis of non-classically damped linear system[J]. Structural Engineering and Mechanics,2002,14(6):679-698.

[2]張淼，于瀾，鞠偉.重頻系統的頻率靈敏度分析算法研究[J].華南師范大學學報:自然科學版,2014，46(3)：39-43.

[3]郭興旺，鄒家祥.對機械振動系統的六種動態響應分析方法的評述[J].振動與沖擊,1996，15(2)：43-46 .

[4]張淼.實模態向量梯度算法[J].長春工業大學學報:自然科學版,2013，34(5)：551-554.

[5]張淼，于瀾，鞠偉.基于頻響函數矩陣計算阻尼系統動力響應的新方法[J].振動與沖擊,2014，33(4)：161-166.

[6]張淼，于瀾，鞠偉.復模態正交性理論的異常現象及對策分析[J].應用數學和力學，2014，35(10)：1081-1091.

[7]SondiponA,FriswellMI.Eigenderivativeanalysisofasymmetricnon-conservativesystems[J].InternationalJournalforNumericalMethodsinEngineering,2001,51(6):709-733.

[8]張淼，于瀾，鞠偉.重頻結構模態靈敏度分析的高精度截模態算法[J].振動工程學報,2014，27(4)：526-532.

Algorithm comparison for the solution of

symmetric non-classical damped system

ZHANG Miao,YU Lan

(School of Science, Changchun Institute of Technology, Changchun 130012， China)

Abstract：Both the frequency response matrix and complex frequency response method are applied to the same problem, for analyzing the transient response, applied condition & range and errors. The features and efficiency of the two algorithms are discussed.

Key words：non-classically damped system; dynamic response; frequency response matrix; label phenomenon.

作者簡介：張淼(1972-)，男，漢族，吉林長春人，長春工程學院副教授，博士,主要從事結構優化及振動控制方向研究,E-mail:zm7209@163.com.

基金項目：吉林省教育廳"十二五"科學技術研究項目(2014336)； 2014年國家級大學生創新創業訓練項目(201411437028)

收稿日期：2014-06-21

中圖分類號：O 321; TB 122

文獻標志碼：A

文章編號：1674-1374(2015)01-0107-04

DOI:10.15923/j.cnki.cn22-1382/t.2015.1.22