管道機器人的驅動單元工藝優化設計

王　月，鐘梓楠* ，呂金賀

(1.北華大學 機械工程學院,吉林 吉林 132013;2.北華大學 汽車與建筑工程學院,吉林 吉林 132013)

?

管道機器人的驅動單元工藝優化設計

王月1，鐘梓楠1*，呂金賀2

(1.北華大學 機械工程學院,吉林 吉林 132013;2.北華大學 汽車與建筑工程學院,吉林 吉林 132013)

摘要：驅動單元的驅動特性和可靠性決定管道機器人的工作效率及其工作能力，由于對管道機器人三軸差速驅動單元的優化大部分都由電腦仿真來完成，但是在制造、裝配階段還是會導致差速不準、功率過大等問題.因此本文通過對三軸差速器工藝的優化，解決了工藝當中的公差分配問題，降低了零件的工藝難度，建立了十字軸垂直度誤差對嚙合質量和軸向調正間隙的函數關系.

關鍵詞：管道機器人；三軸差速器；傳動精度；工藝優化

管道機器人用于工作在管道內部特定的空間里的智能裝備，用來完成管內加工、異物清除、防腐涂層的涂敷、管道缺陷檢測等任務，從管道機器人出現至今，已經有多項研究成果[1-4].而在眾多研究中，為了保證機器人能夠長距離巡線，對管道機器人提出了如下性能要求：①環境適應性好；②驅動效率高；③結構緊湊，功率體積比大；④移動速度快；⑤系統運行可靠性高.

在前期研究過程中，通過對三軸差速驅動單元的仿真分析可知，只要所設計的驅動單元結構對稱就可以保證實現差速功能，但是由于設計、制造和裝配調整不當，還是可能會出現差速不準和功率消耗過大等故障.本文將從工藝優化的角度出發，以提高傳動精度為目標，對典型零件和結構進行工藝優化分析，解決了工藝當中的公差分配問題，降低了零件的工藝難度，建立了十字軸垂直度誤差對嚙合質量和軸向調正間隙的函數關系[5-6].

1三軸差動式驅動單元的結構與機構原理

管道機器人三軸差動式驅動單元由驅動部分和壓緊力調節部分組成.驅動部分由驅動電機驅動三軸差速機構，并由三軸差速機構并聯驅動沿周向120°均布的3個錐齒輪副，錐齒輪又通過同步帶帶動驅動單元的前行走輪組運動，前行走輪組經由同步帶把運動傳遞到后驅動輪組，從而實現驅動單元由一個電機驅動，三路差動輸出的目標.壓緊力調節部分由預緊滑套、支撐桿及平行四桿式驅動輪支架等組成.通過電機驅動，調節彈簧的預壓縮量來調節驅動輪與管壁的接觸壓力，從而使驅動單元獲得足夠的拖動力，且驅動單元可適應一定范圍的管徑變化[7-9].三軸差動式管道機器人驅動單元虛擬樣機如圖1所示.

圖1　三軸差動式驅動單元結構原理圖

2驅動單元的三軸差速機構及其差速特性

2.1　三軸差動式驅動單元的差速機構

如圖2所示，三軸差速機構是由主差速器1、主差速器2、主差速器3及分動器等4個差動輪系組成，具有由單個輸入運動n0轉化成三路差速輸出nii(i=1,2,3)的功能[10-12].

圖2　三軸差動式驅動單元的差速機構

2.2　三軸差動式驅動單元的差速特性

2.2.1三軸差動式驅動單元在直管階段的差速方程

管道機器人驅動單元在直管內運動時，三軸差速器不差速，驅動單元在管內作平動，各行走輪在純滾動狀態下，所有的輪心速度應當一致，且輪心的速度應當等于行走輪的半徑與其旋轉速度的乘積[11].故滿足如下運動方程：

(1)

由方程(1)，可確定驅動單元在直管階段各行走輪的轉速.

2.2.2三軸差動式驅動單元在彎管階段的差速方程

圖2所示為驅動單元在彎管階段的差速原理，由于管道機器人自身對稱性的特點，前行走輪組輪心所確定的管道截面圖形與后行走輪組輪心所確定的管道截面圖形是完全相同的，對應的前后行走輪的速度也必然是相等的，

vfi=Rfiω=vri=Rriω=0.5dnii

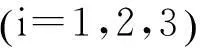
因此有：

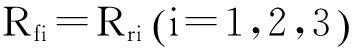
(2)

vf1:vf2:vf3=Rf1:Rf2:Rf3=n11:n22:n33

(3)

vr1:vr2:vr3=Rr1:Rr2:Rr3

(4)

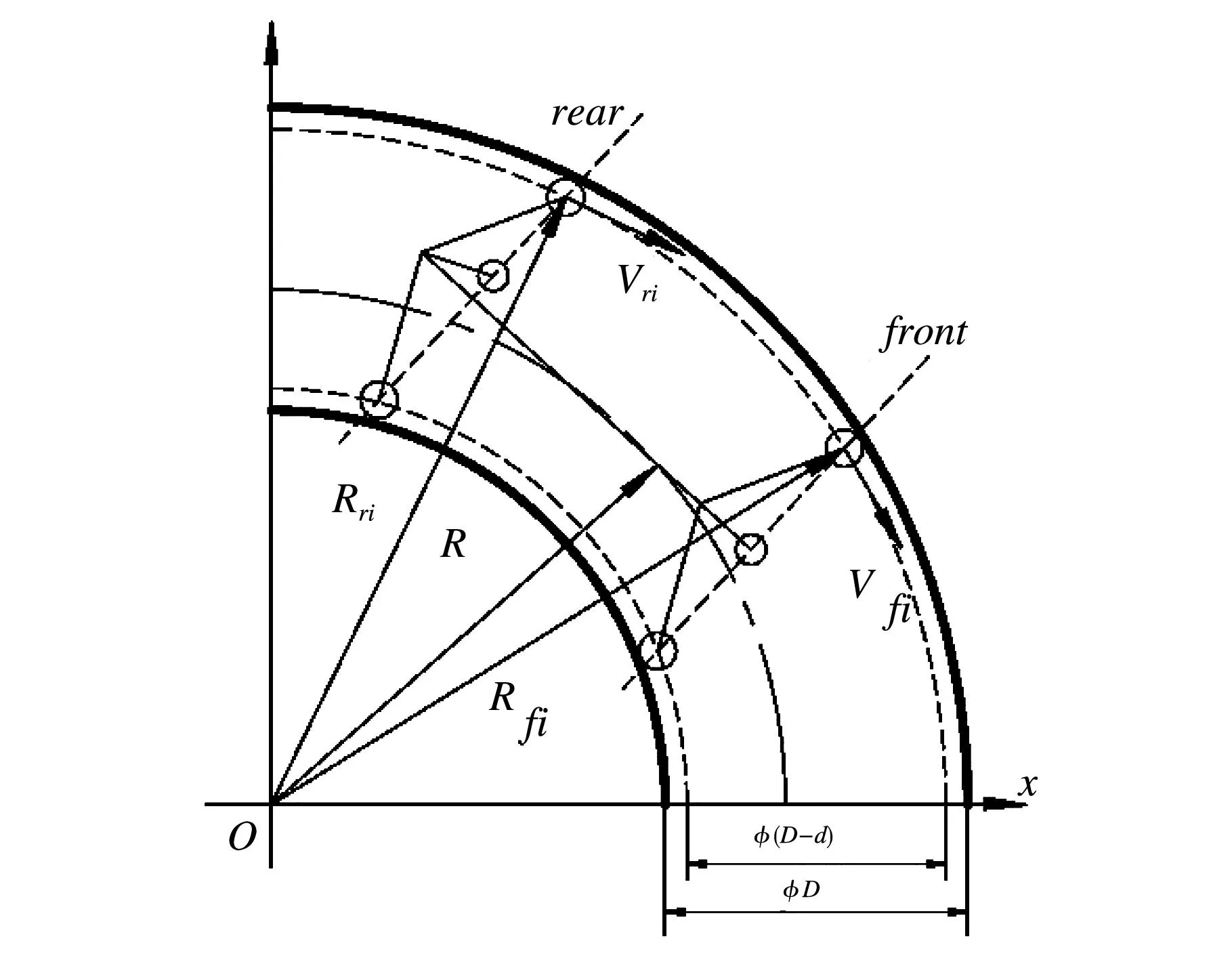
圖3　驅動單元彎管階段差速原理

3三軸差速器零件及工藝進行優化

3.1　驅動單元支撐板孔系加工中的工藝優化設計

計算平面尺寸鏈的常用方法有：卡具法、投影法和極值法，但是這些方法很難應用于幾個互相成一定角度的工藝尺寸，特別是含有角度公差的情況.在三軸差動式驅動單元試制過程中，有三件形狀類似的零件，對前支撐板為孔系進行計算發現，上述方法分配的公差值都不近合理，要么浪費了工藝能力，要么出現工藝能力不足等情況，而采用偏微分方程導出的多元函數微分學公式，使用起來方便有效，滿足了工藝要求.

以中心輪的中心B為坐標原點建立參考坐標系，電動機上的主驅動輪中心A和行星輪中心C的坐標值如圖所示，不必進行計算即可得知.現在只要計算出另外兩個行星輪的中心點D和E的坐標值及公差值就可以解決加工中的工藝問題.

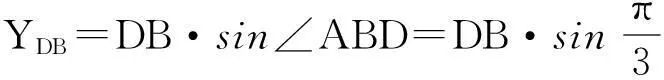
(5)

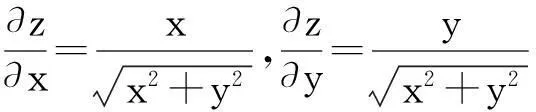
(6)

(7)

故得

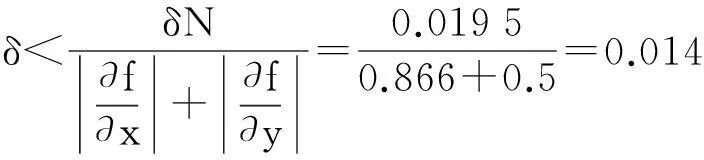
(8)

由于采用了等公差原則，所以把兩者取成一致并向小值方向圓整.所以取：δx=δy=±0.014

(2) 驗算

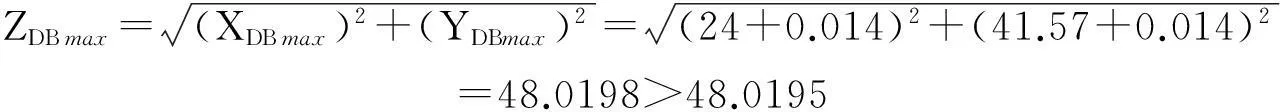
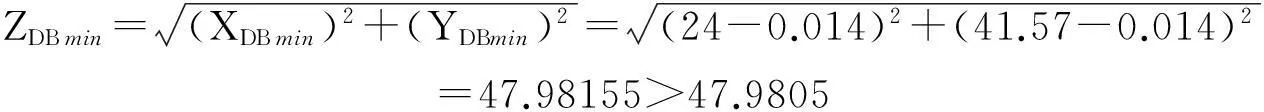
(3) 重新驗算

上述計算的結果雖然不合理，但是相差甚微，為了保障有足夠的工藝能力，需要進行重新驗算，故令δx=δy=±0.013

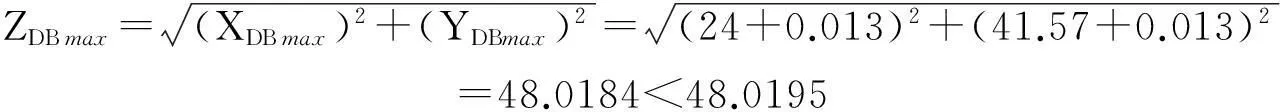
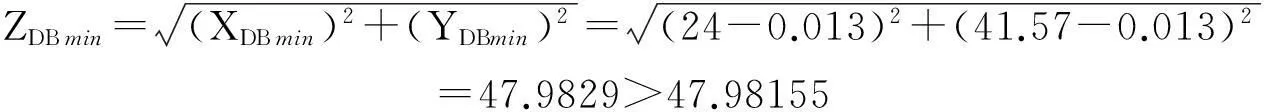
以上的計算結果表明：

XDB=24±0.013，YDB=41.57±0.013.

(9)

計算的結果可以應用到數控銑床或坐標鏜床上，也可以用在有數顯裝置的銑床或普通銑床上，均可以保證加工的精度要求.采用同樣的方法可以求出E點的坐標值和相應的公差值，計算過程略.

經過上述理論計算及實際應用可知，把偏微分方法引入到三軸差速驅動單元支撐板的孔系加工工藝計算中，各個縱橫坐標的偏差分配合理，可以把精度要求較高的零件從高精度機床上移至普通機床上進行加工，拓寬了機床的工藝能力，發揮了其潛在的經濟效益，降低了科研開發的周期和成本，此計算方法同樣可以應用到其它類似的孔系零件加工.

3.2　驅動單元裝配中的工藝優化設計

如圖4所示，正常嚙合時4個圓錐齒輪1、2、3和4的分度圓錐對稱于x與y坐標軸，當十字軸存在垂直度誤差時，分度圓錐則對稱于坐標原點O，圓錐齒輪1和2之間的分度圓錐位置間的距離即為a1e1和a1j1直線之間的距離，最小值在a1點，最大值為e1和j1之間的距離.a1點的坐標為：

圖4　分動器機構十字軸垂直度誤差分析簡圖

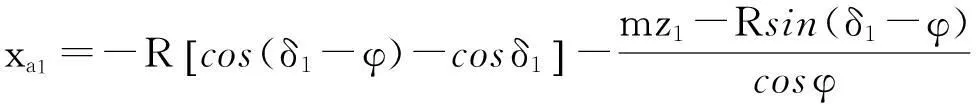
由圖4可見，圓錐齒輪1和2之間的分度圓錐在此處重合，其位置間的距離為零.e1點的坐標為：

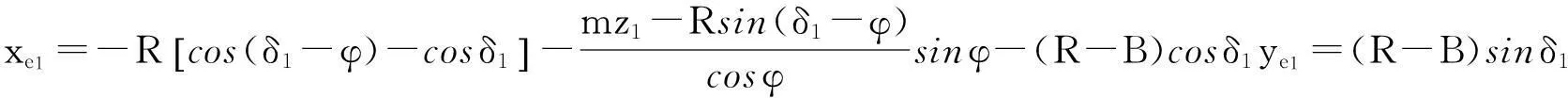
j1點的坐標為：

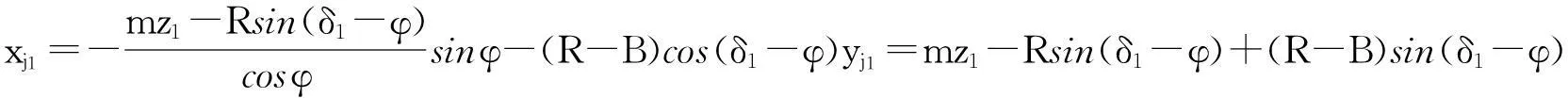
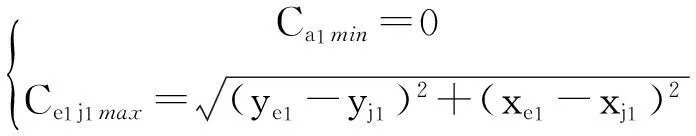
(10)

圓錐齒輪1和4之間的分度圓錐位置間的距離即為g1k1和c2f2直線之間的距離，最大值為g1和c2之間的距離，最小值為k1和f2之間的距離.

g1點的坐標為：

c2點的坐標為：

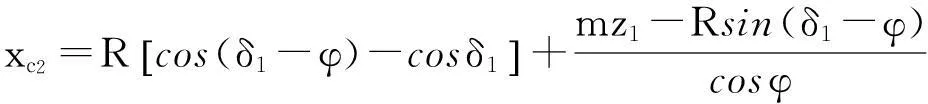
yc2=Rsinδ1

k1點的坐標為：

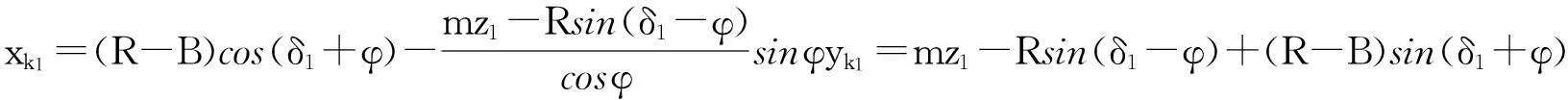
f2點的坐標為：

yf2=(R-B)sinδ1

則：圓錐齒輪1和3之間的齒頂隙變化量

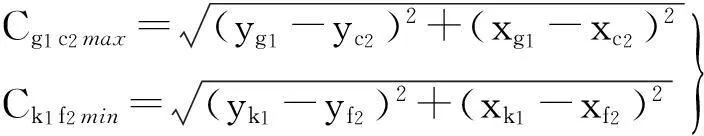
(11)

由圖4可以看出圓錐齒輪2和3之間的分度圓錐位置間的距離變化量與圓錐齒輪1和4之間的距離變化量相同，圓錐齒輪3和4之間的分度圓錐位置間的距離變化量與圓錐齒輪1和2之間的分度圓錐位置間的距離變化量也相同，且它們之間是對稱于坐標原點的.

從上述的分析結果可以看出，當十字軸存在垂直度誤差時即影響圓錐齒輪副的嚙合質量又影響裝配時的軸向調正間隙，所以在設計與加工裝配中應當根據實際情況選用合理的形位公差，并且在采用有效的加工工藝，這樣才能保證裝配質量，直至保證差動機構的傳動精度.

4結論

通過對三軸差動機構中的支撐板和十字軸組件進行工藝優化分析，解決了如下問題：

(1) 用偏微分法解決了工藝當中的公差分配問題，降低了零件的工藝難度，這樣即使是在普通機床上也能保證零件的加工質量，節約了科研經費，減少了加工周期.

(2) 系統詳細地分析了十字軸存在垂直度誤差時對圓錐齒輪副的嚙合質量和裝配時的軸向調正間隙的影響，建立了十字軸垂直度誤差對嚙合質量和軸向調正間隙的函數關系，在可靠性分析中能夠定量分析管道機器人三軸差動式驅動單元傳動精度.

參考文獻：

[1]Shuxiang Guo and Yasuhiro Sasahi.A New Kind of Microrobot in Pipe Using Driving Fin[J].Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2003:697-702.

[2]Shuxiang Guo.A New Type of Microrobot for Biomedical Application[J].Proceedings of the 2004 IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2004:867-872.

[3]楊斌久,姜生元,耿德旭,等.三軸差速器的設計及應用[J].吉林大學學報:工學版,2002,32(4):70-75.

[4]張玉峰，姜生元，李建永，等.介質流壓差驅動式管道機器人的驅動、調速原理分析及結構設計[J].吉林化工學院學報，2009,26(2):85-88.

[5]張學文,賈亞洲,鄧宗全,等.管道機器人三軸差動式驅動單元的設計研究[J].機器人,2008,30(1):22-28.

[6]盧偉宏，王海波，孟慶鑫.一種教學機器人控制系統研發[J].吉林化工學院學報，2009,26(4):67-69.

[7]唐德威,梁濤,姜生元,等.機械自適應管道機器人的機構原理與仿真分析[J].機器人,2008,30(1):29-33.

[8]張學文,賈亞洲,姜生元,等.管內移動機器人三軸差動單元可靠性分析[J].吉林大學學報:工學版,2008,38(2):365-369.

[9]湯婷潔,李朝東.微型管道機器人及其電驅動技術[J].微特電機,2005(4):36-38.

[10] 朱敬德,周明,應金貴,曾俊冬.在役石油管道檢測機器人機械設計[J].上海大學學報(自然科學版),2001,7(1):57-59.

[11] Riggins R,Snider J,Mutter B.Design and analysis of an autonomous ground robotic vehicle[J].AUVSI's Unmanned Systems North America,2004-Proceedings:295-309.

[12] Korayem M.H,Rostam T.Bani,Nakhai A.Design,modeling and errors measurement of wheeled mobile robots[J].International Journal of Advanced Manufacturing Technology,2006,28(3-4):403-416.

Pipeline Robot Drive Unit Process Optimization Design

WANG Yue1,ZHONG Zi-nan1*,LV Jin-he2

(1.College of Mechanical Engineering,Beihua University,jilin City 132013,China;2.College of Automotive and Architectural Engineering,Beihua University,Jilin City 132013,China)

Abstract:The driving characteristics and reliability of the drive unit determine the working efficiency of the pipeline robot and its working ability,as a result of the optimization of pipeline robot tri-axial differential drive unit mostly are done by computer simulation,but in the manufacturing and assembly phase will lead to inaccurate differential,too much power.So in this paper,through optimizing the tri-axial differential technology,solving the problem of tolerance allocation among technology,reducing the parts of the technology difficulty,cross axis perpendicularity error on the meshing quality and a function of the axial adjustment clearance is established.

Key words:pipeline robot；tri-axial differential；transmission accuracy；process optimization

文章編號：1007-2853(2015)11-0050-05

通信作者：*曹亮，E-mail:caoliang@cust.edu.cn

作者簡介：關會英(1980-)，女，吉林省吉林市人，吉林化工學院講師，博士，主要從事工程仿生學、工程圖學及CAD教學與研究方面的工作。

收稿日期：2015-07-20

中圖分類號：TP 24

文獻標志碼：B DOI：10.16039/j.cnki.cn22-1249.2015.11.012