多點激勵正弦振動的實數域控制算法研究①

劉志華， 蔡晨光， 于 梅， 夏 巖， 李京勝

(中國計量科學研究院， 北京 100029)

多點激勵正弦振動的實數域控制算法研究①

劉志華， 蔡晨光， 于 梅， 夏 巖， 李京勝

(中國計量科學研究院， 北京 100029)

多點激勵正弦振動系統能更加真實地模擬實際振動環境，更利于掌握產品的實際振動特性。針對傳統頻域迭代算法中復數計算的求解復雜性，對實數域控制算法進行研究。建立多點激勵正弦振動控制的實數域數學模型，采用Broyden算法構建實數形式的阻抗矩陣，并對迭代步長進行優化，在此基礎上提出實數域迭代算法的控制流程。最后對算法的可行性進行仿真分析和實驗驗證，結果表明：實數域控制算法的收斂速度快、響應精度高，且可以有效避免振蕩過沖現象。

振動控制； 多點激勵； 擬牛頓算法； 實數域

引 言

傳統的振動環境試驗廣泛采用單點激勵振動系統，但隨著產品結構的復雜化和多樣化，人們逐漸開始關注多點激勵振動系統，其優勢在于不僅能夠提供足夠的推力而且能更加真實地模擬實際振動環境，更利于掌握產品的實際振動特性[1-2]。正弦振動試驗是一類重要的振動環境試驗，有助于暴露零部件或設備在特定激勵頻率下的故障缺陷[3]。相比于單點正弦激勵控制，多點激勵正弦振動控制除了要控制激勵點幅值大小，還需考慮各激勵點之間的互耦補償以及相位差修正[4-5]。因此，多點激勵正弦振動控制具有一定的難度與挑戰性。

多點激勵正弦振動控制的研究始于1973年，Fisher論述了互耦補償方式的多點激勵數字控制的理論與實踐，為多點激勵振動控制提供了理論依據[6]。Hamma和Smith提出了線性控制算法，采用誤差頻譜和當前驅動頻譜之和來修正命令驅動頻譜，算法簡單但穩定性較差[7]。Chen和Wilson采用迭代增益來控制誤差頻譜補償量，提高了正弦振動控制的穩定性但卻減慢了收斂速度[8]。目前廣泛應用的控制方法為提前激勵系統來測量估計系統頻響函數，進一步計算阻抗矩陣，完成對驅動信號的迭代修正[9-10]。但此類方法采用固定的迭代增益和阻抗矩陣，初始的阻抗矩陣誤差會對控制系統的穩定性和精度產生持續性影響[11]。Underwood提出多點激勵正弦試驗的自適應控制方法，通過可變增益來控制迭代步長，并在迭代中不斷更新系統阻抗矩陣，補償系統的非線性和時變性影響[12-13]。國內學者陳家焱提出多點激勵正弦振動的最優控制策略，以響應譜和參考譜的誤差矢量范數為目標函數，采用“雙步控制閉環”方法來確定并優化控制系統的迭代步長和驅動信號[14]。然而現存控制方法均為頻域迭代算法，系統傳遞函數為復數矩陣，需要在復數域空間確定迭代步長和阻抗矩陣，增加了控制算法復雜度。

本文針對傳統頻域迭代算法的不足，提出多點激勵正弦振動控制的實數域控制算法。首先，建立正弦振動的實數域控制數學模型，根據系統響應構建阻抗矩陣，并對迭代步長進行優化，在此基礎上給出實數域迭代算法的控制流程。最后，對實數域迭代算法進行仿真分析，并通過實驗進行驗證。

1 實數域控制算法

1.1 數學模型

傳統的多點激勵正弦振動控制方法為頻域迭代算法，如圖1所示，需要提前激勵系統來獲取頻響函數估計并計算阻抗矩陣，控制目標為使測量的響應頻譜達到理想的參考頻譜，通過反復迭代修正驅動信號，使系統輸出的響應信號不斷趨近設定的參考信號，驅動頻譜的修正方程可以描述為

Dn+1(f)=Dn(f)+αZ(f)(R(f)-Cn(f))

(1)

式中Dn(f)為第n次迭代驅動譜；Dn+1(f)為所求的第n+1次迭代驅動譜；Z(f)為系統阻抗矩陣，通常取為系統頻響函數估計值A(f)的逆矩陣A-1(f)；α為迭代增益，由于估計的頻響函數與真實的頻響函數難免存在一定誤差，因此通常選取迭代增益0<α<1以提高控制系統的穩定性。

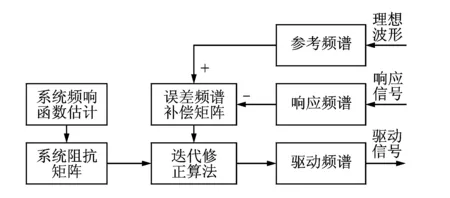
圖1 頻域迭代算法Fig．1 Iterative method in the frequency domain

傳統頻域迭代算法所開展的提前激勵增加了振動控制過程的額外工作量，多點激勵振動系統的頻響函數識別往往耗時較長，明顯增加了振動試驗時間，而且還可能會對一些精密或易碎的試驗樣本造成不必要的損壞[15]。除此之外，傳統頻域迭代算法基于系統頻響函數，多點激勵振動系統的頻響函數為復數域矩陣，限制了一些較為有效的實數域算法在振動控制領域的應用。因此，為了避免頻域迭代算法的提前激勵，將采用實數域控制算法來解決多點激勵正弦振動控制問題。

系統的頻響函數h(f)是一個包含幅值α和相位β的復指數

h(f)=αejβ

(2)

系統在頻率ω、幅值C和相位φC的正弦信號x(t)激勵下，將輸出同頻率的正弦信號y(t)：

x(t)=Csin(ωt+φC)

(3)

y(t)=αCsin(ωt+φC+β)

(4)

任意的正弦輸入信號都可以變換成如下形式

(5)

其中，w1和w2為輸入系數

w1=Ccos(φC),w2=Csin(φC)

(6)

同樣，任意的正弦輸出信號也可以變換為

(7)

其中，u1和u2為輸出系數

(8)

通過式(5)和(7)的變換，系統的輸入和輸出均被表示成相互正交的正余弦函數之和的形式，如圖2(a)所示，而輸入和輸出信號的幅值和相位由正余弦函數的系數決定。由于輸入和輸出均為標準正弦信號，振動控制中往往僅關心其幅值和相位，因此可將系統進行簡化，如圖2(b)所示，其中輸入為u(t)，輸出為w(t)，傳遞特性為h(t)，則由式(8)可以得到

u(t)=h(t)w(t)

(9)

其中：

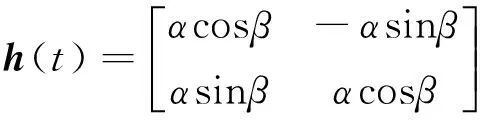
(10)

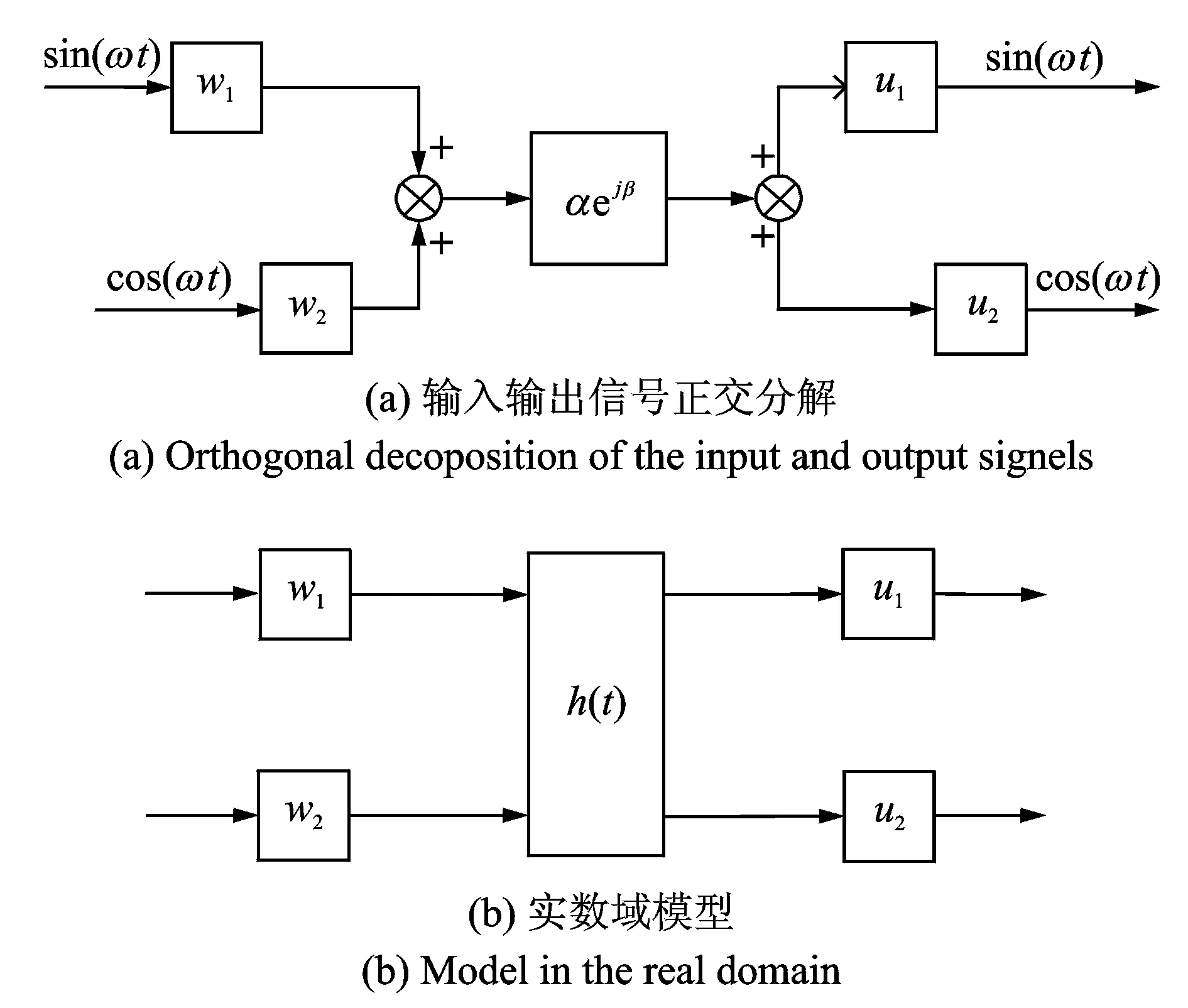
圖2 系統模型化簡Fig．2 Simplified system model

式(9)所描述的系統傳遞模型采用兩個實系數來代替原本的一維正弦信號，雖然增加了系統的維度，但沒有添加任何額外信息，因為正弦信號包含了幅值和相位。若不增加維度就要采用包含實部和虛部的復數表示，由此提出的復數域控制算法往往較為復雜。式(9)通過增加維度將復數域問題轉換成實數域問題，便于實數域控制算法的提出。

同理，可以建立多點激勵正弦振動系統的實數域數學模型

C(t)=H(t)D(t)

(11)

式中D(t)為系統驅動系數，C(t)為系統響應系數，H(t)為系統傳遞特性。

(12)

式中ui(t)為激勵點i的響應系數，wi(t)為激勵點i的驅動系數，hij(t)為激勵點j和激勵點i之間的傳遞特性，m為激勵點的總個數。

1.2 阻抗矩陣

假設系統的參考系數為R(t)，系統的響應系數為C(t)，可以定義系統的誤差系數如下

F(D(t))=R(t)-C(t)=

R(t)-H(t)D(t)

(13)

多點激勵正弦振動控制的目標為求解合理的驅動系數D(t)，使得響應系數C(t)盡量接近參考系數R(t)，即求解方程F(D(t))=0。若不進行提前激勵，無法獲得系統的傳遞特性H(t)，因此將無法直接求解方程F(D(t))=0的導數值，只能獲得方程函數值，此時可采用如下擬牛頓方法進行求解[16]

(14)

其中：

sn+1(t)=Dn+1(t)-Dn(t)，

yn+1(t)=F(Dn+1(t))-F(Dn(t))

(15)

式(14)中An+1(t)是對方程導數矩陣F′(D(t))的近似，通過修正矩陣ΔAn(t)迭代求得。但式(14)必須在增加適當條件下才能完全確定An+1(t)。Broyden算法要求An+1(t)和An(t)在向量sn+1(t)的正交補上二者無任何差別，即

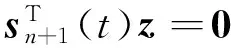
(16)

假定u(t)為待定向量，則由式(16)可以得到

(17)

由式(14)中的方程二可以得到

(An+1(t)-An(t))sn+1(t)=

yn+1(t)-An(t)sn+1(t)

(18)

將式(17)的兩邊右乘sn+1(t)，并聯立式(18)可得到

(19)

將式(19)得到的u(t)代入式(17)便可得到An+1(t)的修正方程

(20)

根據式(20)對An+1(t)進行修正后，還需要通過求解線性方程組才能獲得驅動系數Dn+1(t)。為了求解方便，根據Sherman-Morrison定理[16]可對An+1(t)的逆矩陣Zn+1(t)進行更新

(21)

通常將Zn+1(t)稱為系統的阻抗矩陣，它是一個有別于傳統頻域迭代算法中的阻抗矩陣的實數矩陣。于是可以獲得驅動系數的修正方程如下

Dn+1(t)=Dn(t)-Zn(t)(R(t)-Cn(t))

(22)

式(21)和(22)即為求解實數域非線性方程組的Broyden算法，在多點激勵正弦振動控制應用中不需要進行系統辨識，從而避免了提前激勵。

1.3 迭代步長

理論上按照式(22)的迭代公式便能夠求解得出滿足系統響應要求的驅動系數Dn+1(t)，而阻抗矩陣Zn(t)在迭代過程中將逐漸趨近于傳遞特性H(t)的逆矩陣。由于迭代開始階段的阻抗矩陣往往與H(t)的逆矩陣偏差較大，因此采用失真的阻抗矩陣修正的驅動系數會造成系統響應的振蕩，而在實際控制中應該盡量避免這種情況的出現。為此將式(22)的驅動系數迭代公式修改如下

Dn+1(t)=Dn(t)-λZn(t)(R(t)-Cn(t))

(23)

式中λ為迭代步長，用以合理控制驅動系數的修正量。如圖3所示，阻抗矩陣Zn(t)決定了驅動系數的修正方向，而迭代步長λ則決定了驅動系數的修正量，事實上任意修正方向上均存在一個最接近目標值的局部極點，此局部極點可通過尋優迭代步長求得，以本局部極點為起點沿更新的阻抗矩陣方向，通過尋優迭代步長便可求得下一個局部極點，隨著迭代過程局部極點將逐漸靠近目標值。所求得的局部極點是當前修正方向下最接近目標值的驅動系數，從而有效避免了控制過程的振蕩現象。

將誤差系數的矢量范數作為目標函數，用以衡量響應系數C(t)與參考系數R(t)的接近程度

f(Dn+1(t))=(R(t)-Cn+1(t))T(R(t)-Cn+1(t))

(24)

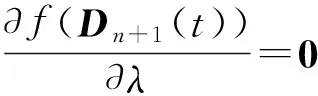
λ=-{H(t)Zn(t)(R(t)-Cn(t))]T(R(t)-Cn(t))}/

{H(t)Zn(t)(R(t)-Cn(t))]T[H(t)Zn(t)(R(t)-Cn(t))}

(25)

式(25)的迭代步長求解表達式中包含有未知的系統傳遞特性H(t)，因此需要根據系統響應系數對系統的傳遞特性進行估計。為準確估計當前狀態系統傳遞特性，驅動系數的變化量應盡可能小，采用取值很小的迭代步長ρ(通常為0.1)修正驅動系數

(26)

由式(27)可以進一步推導得出

H(t)Zn(t)(R(t)-Cn(t))=

(28)

將式(28)代入式(25)可以消去方程中的未知量，得到最優步長的求解公式如下

(29)

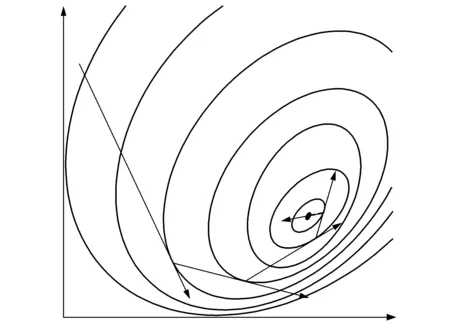
圖3 步長尋優Fig．3 Step optimization

1.4 控制流程

綜合上述分析，給出多點激勵正弦振動實數域控制算法的實現流程如圖4所示，具體步驟如下：

第一步：根據各激勵點的幅值和相位要求設定參考系數R(t)，初始化迭代條件：D0(t)=0m，C0(t)=0m，Z0(t)=Im。

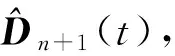
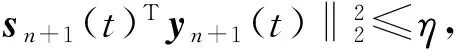
第四步：判斷迭代次數是否超過規定最大次數限制，若超過結束特定頻率的閉環控制，否則返回第二步，進入下一循環。

2 仿真與實驗研究

2.1 仿真分析

下面利用Matlab軟件對本文所提出的實數域控制算法的性能進行仿真分析。假設4點激勵振動系統的頻率響應矩陣為

正弦振動控制目標為：激勵點1的參考幅值4.0 m/s2，參考相位60°；激勵點2的參考幅值2.0 m/s2，參考相位120°；激勵點3的參考幅值5.0 m/s2，參考相位30°；激勵點4的參考幅值3.0 m/s2，參考相位90°。

采用Broyden算法按照式(22)修正驅動系數時，仿真得到多點激勵振動系統的幅值響應如圖5所示，相位響應如圖6所示。可以看出，經過16次控制迭代后，激勵點1的幅值和相位便分別趨近于4.0 m/s2和60°；激勵點2的幅值和相位分別趨近于2.0 m/s2和120°，激勵點3的幅值和相位便分別趨近于5.0 m/s2和30°；激勵點4的幅值和相位分別趨近于3.0 m/s2和90°。仿真結果說明Broyden算法能夠高效迭代得出滿足系統響應要求的驅動系數。但圖5中各激勵點的幅值響應在迭代初始階段出現了嚴重的過沖，激勵點1的峰值達到70 m/s2，激勵點2的峰值達到60 m/s2，激勵點3的峰值達到85 m/s2，激勵點4的峰值也已超過55 m/s2，在實際振動控制中容易造成系統的損壞。因此Broyden算法雖然理論效果明顯，卻并不適用于實際的振動控制。

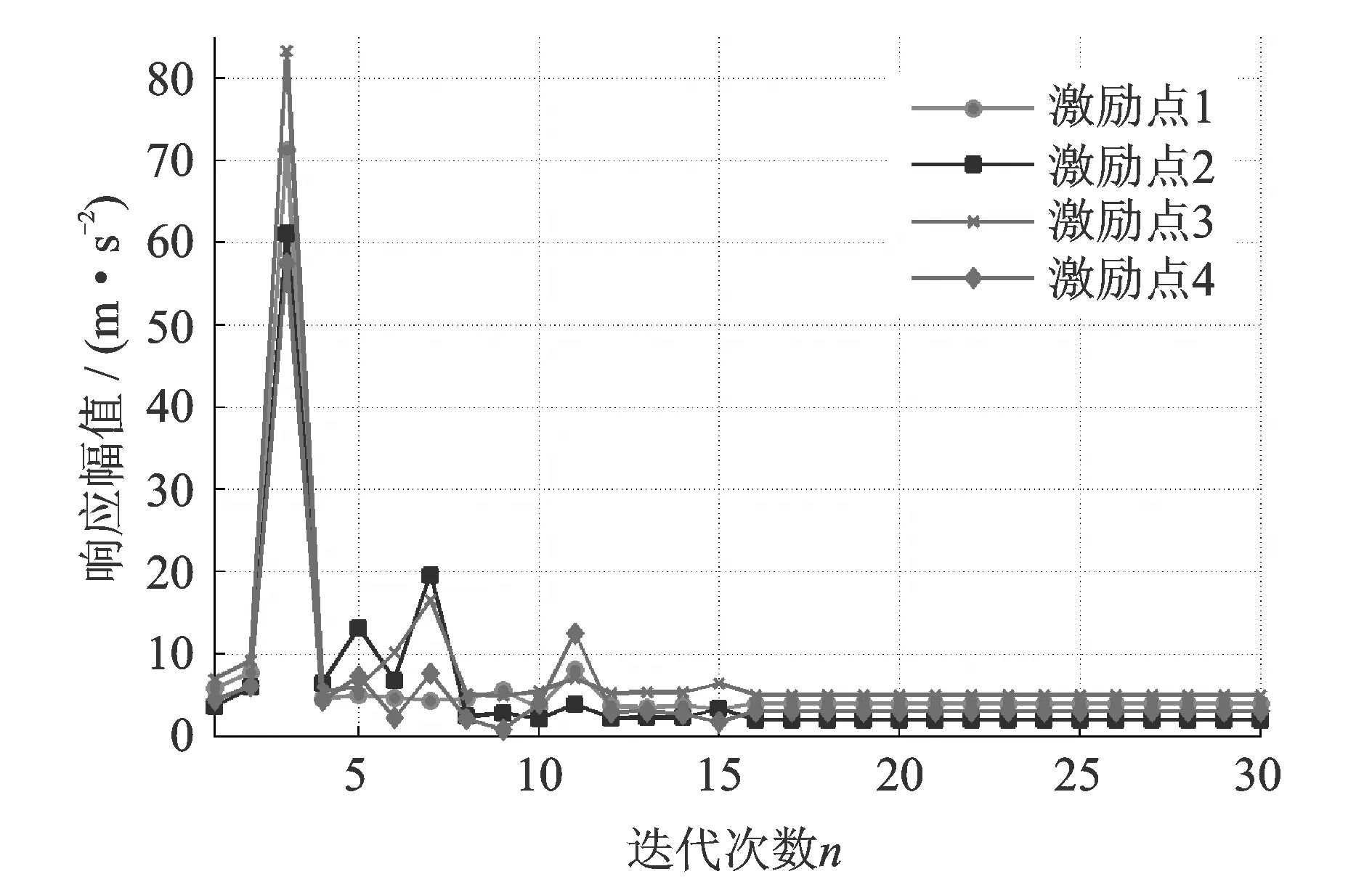
圖5 Broyden算法的幅值響應Fig．5 Amplitude response of the Broyden method

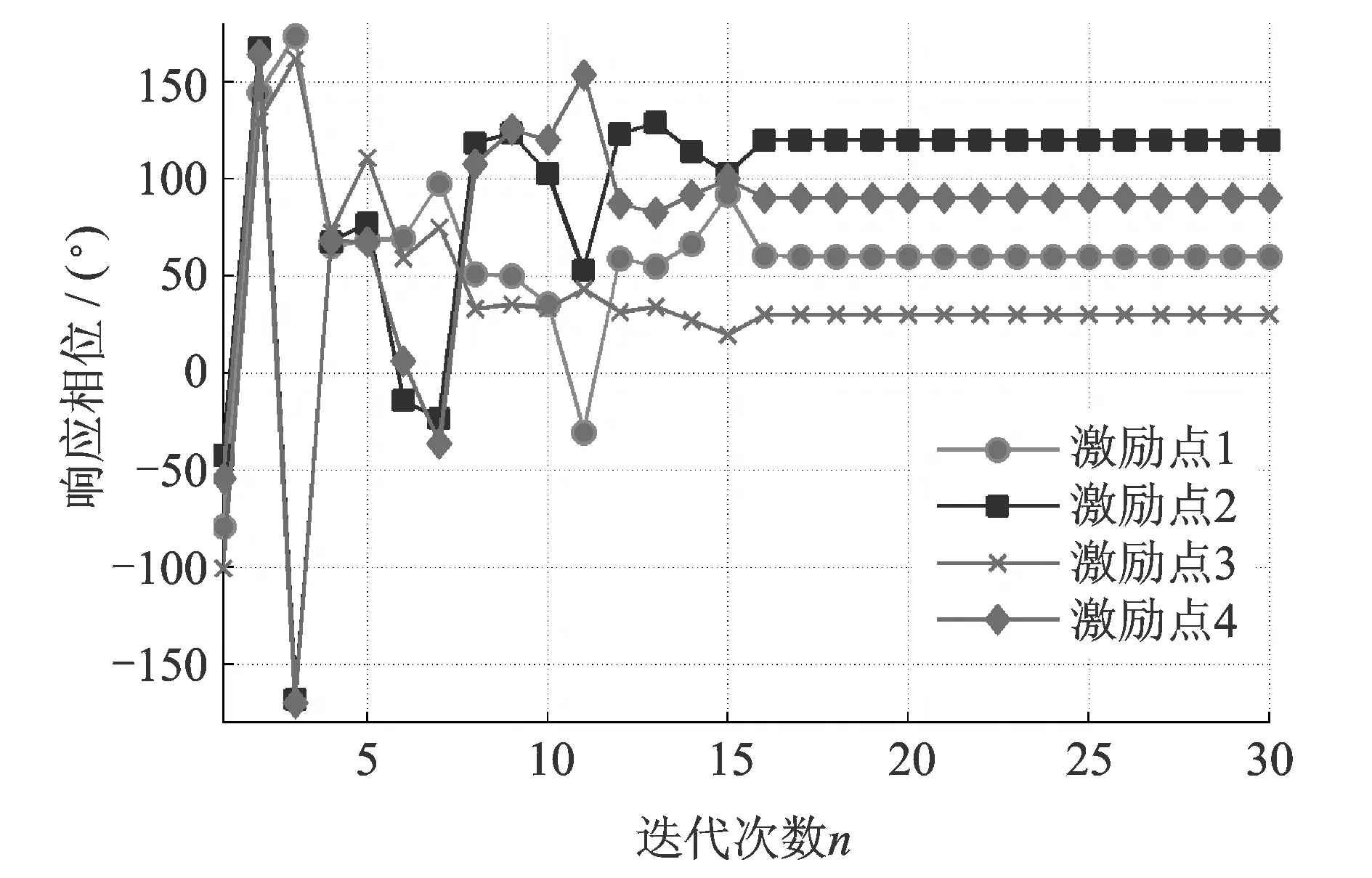
圖6 Broyden算法的相位響應Fig．6 Phase response of the Broyden method

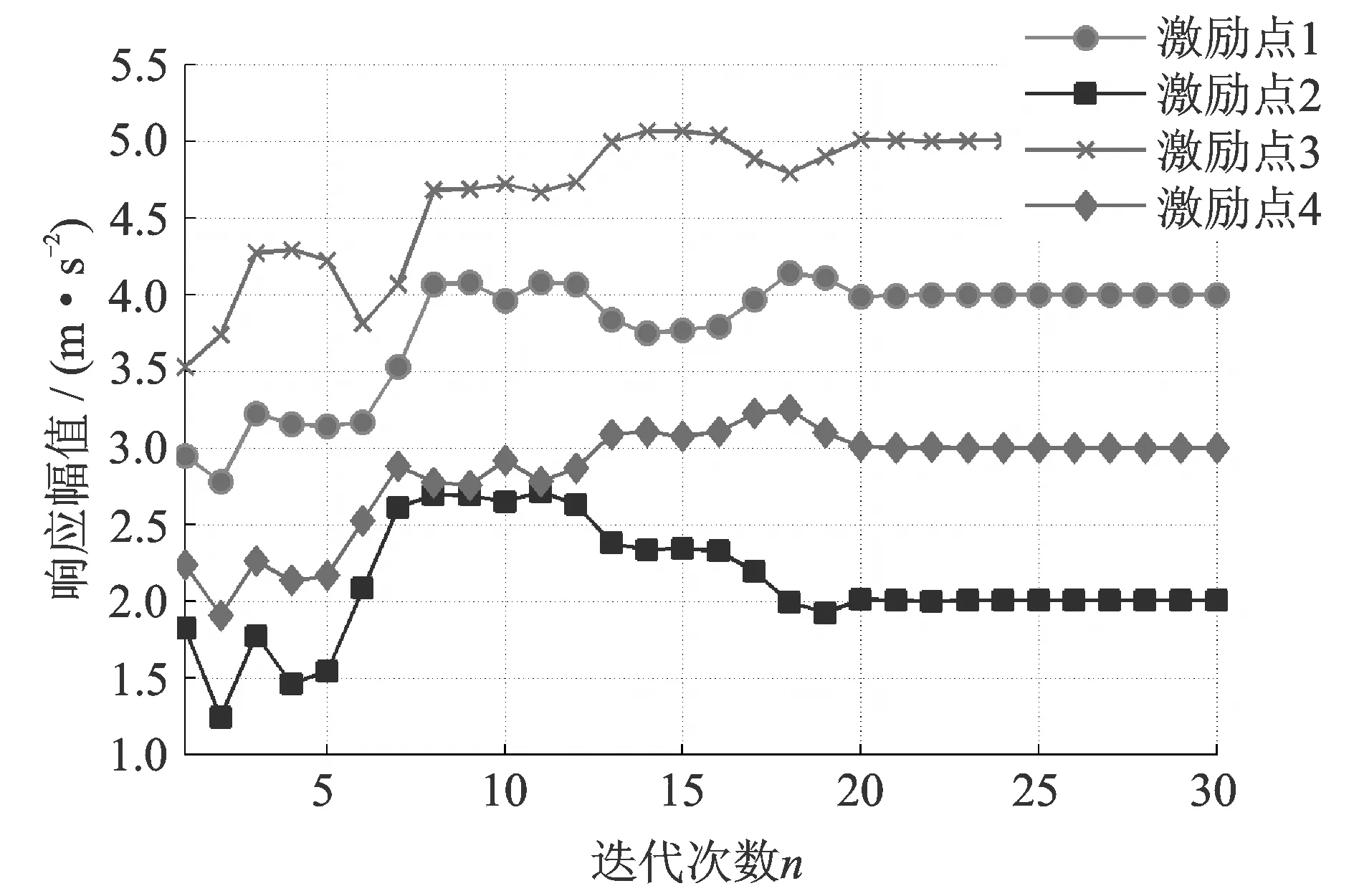
圖7 步長尋優算法的幅值響應Fig．7 Amplitude response of the step optimization method

采用圖4所示的包含步長尋優的實數域迭代算法進行控制時，仿真得到的幅值響應和相位響應分別如圖7和8所示。可以看出，各激勵點的幅值響應迭代初始階段的過沖得到了明顯改善，激勵點1的過沖小于0.15 m/s2，激勵點2的過沖小于0.70 m/s2，激勵點3的過沖小于0.07 m/s2，激勵點4的過沖小于0.25 m/s2。

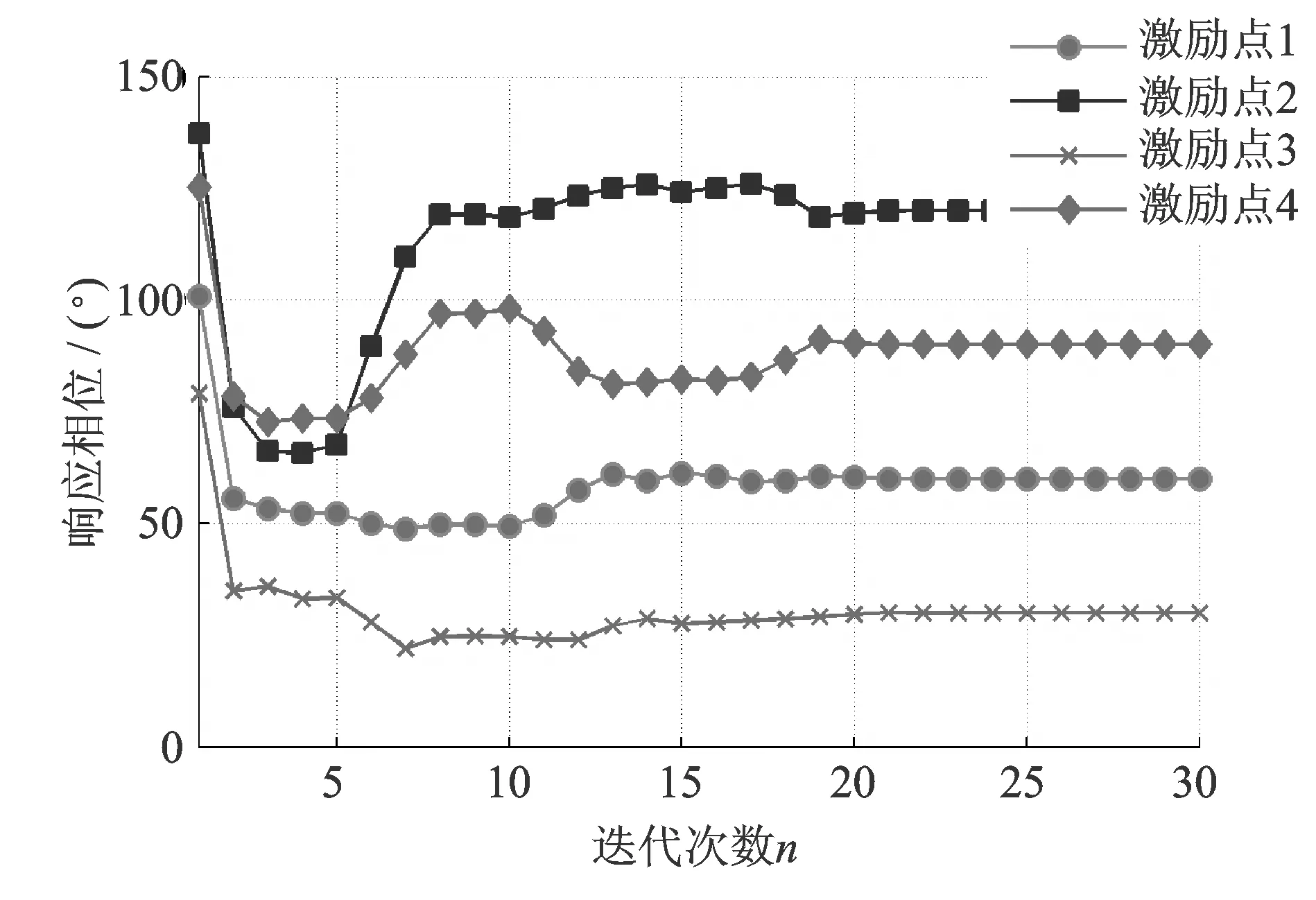
圖8 步長尋優算法的相位響應Fig．8 Phase response of the step optimization method

誤差系數的范數變化如圖9所示，不斷減小的誤差系數范數說明驅動系數在迭代修正一直朝著目標方向進行，不存在振蕩現象。如圖7和8所示，經過20次迭代后，各激勵點的幅值和相位也均趨近于各自的參考幅值和相位。仿真結果說明本文提出的實數域控制算法能夠有效地完成多點激勵正弦振動控制。

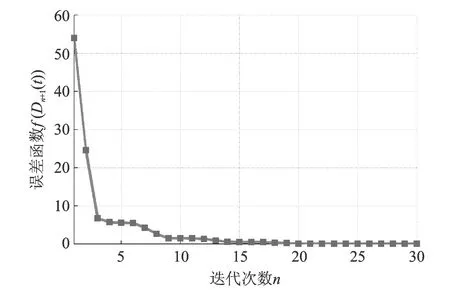
圖9 步長尋優算法的誤差范數Fig．9 Error norm of the step optimization method

2.2 實驗驗證

為了驗證實數域控制算法的可行性，搭建兩點激勵振動系統進行試驗研究，如圖10所示。通過兩個振動臺同時激振三角橫梁，橫梁激勵點附近安裝加速度計實時測量振動大小，經電荷放大器轉換成電壓信號，振動控制器根據控制算法生成模擬電壓信號，通過功率放大器驅動兩振動臺產生振動。

圖10 兩點激勵振動系統Fig．10 Two exciters vibration system

首先，控制兩振動臺輸出頻率為320 Hz的正弦振動，其中激勵點1的幅值為1.2g、相位為60°，激勵點2的幅值為1.0g、相位為90°。采用圖4所示的實數域迭代算法進行控制，得到的幅值和相位響應分別如圖11和12所示。可以看出，經過15個迭代步長，激勵點1的幅值和相位便分別趨近于1.2g和60°，迭代初始階段沒有出現幅值響應過沖；經過15個迭代步長激勵點2的幅值和相位分別趨近于1.0g和90°，迭代初始階段幅值響應的過沖小于0.2g。經過30個迭代步長兩激勵點幅值和相位的穩態誤差均小于0.001g和0.1°，實驗說明實數域迭代算法在320 Hz頻率點具有良好的精度和速度，能有效避免振蕩過沖現象。

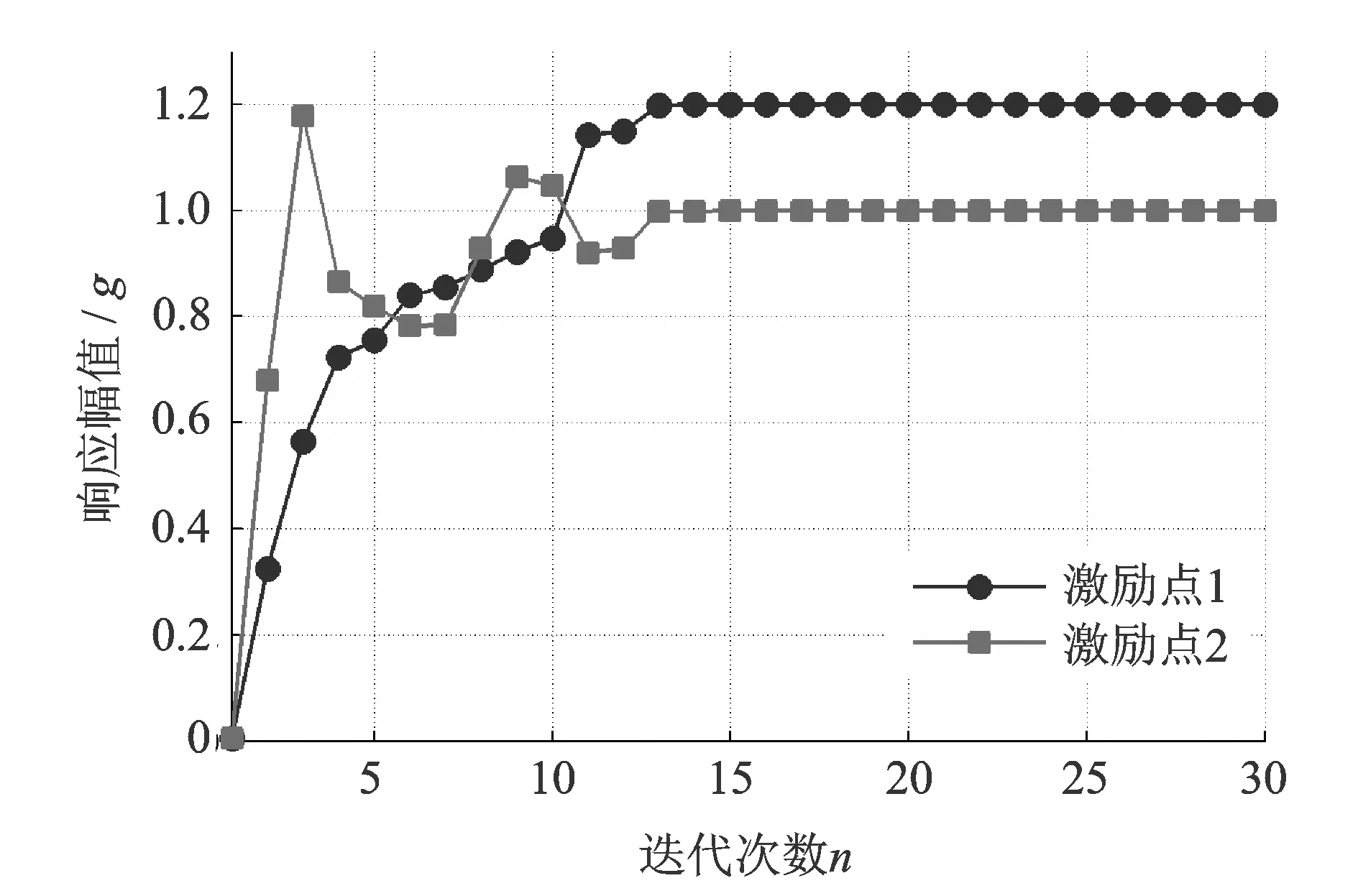
圖11 320 Hz幅值響應Fig．11 Amplitude response at 320 Hz

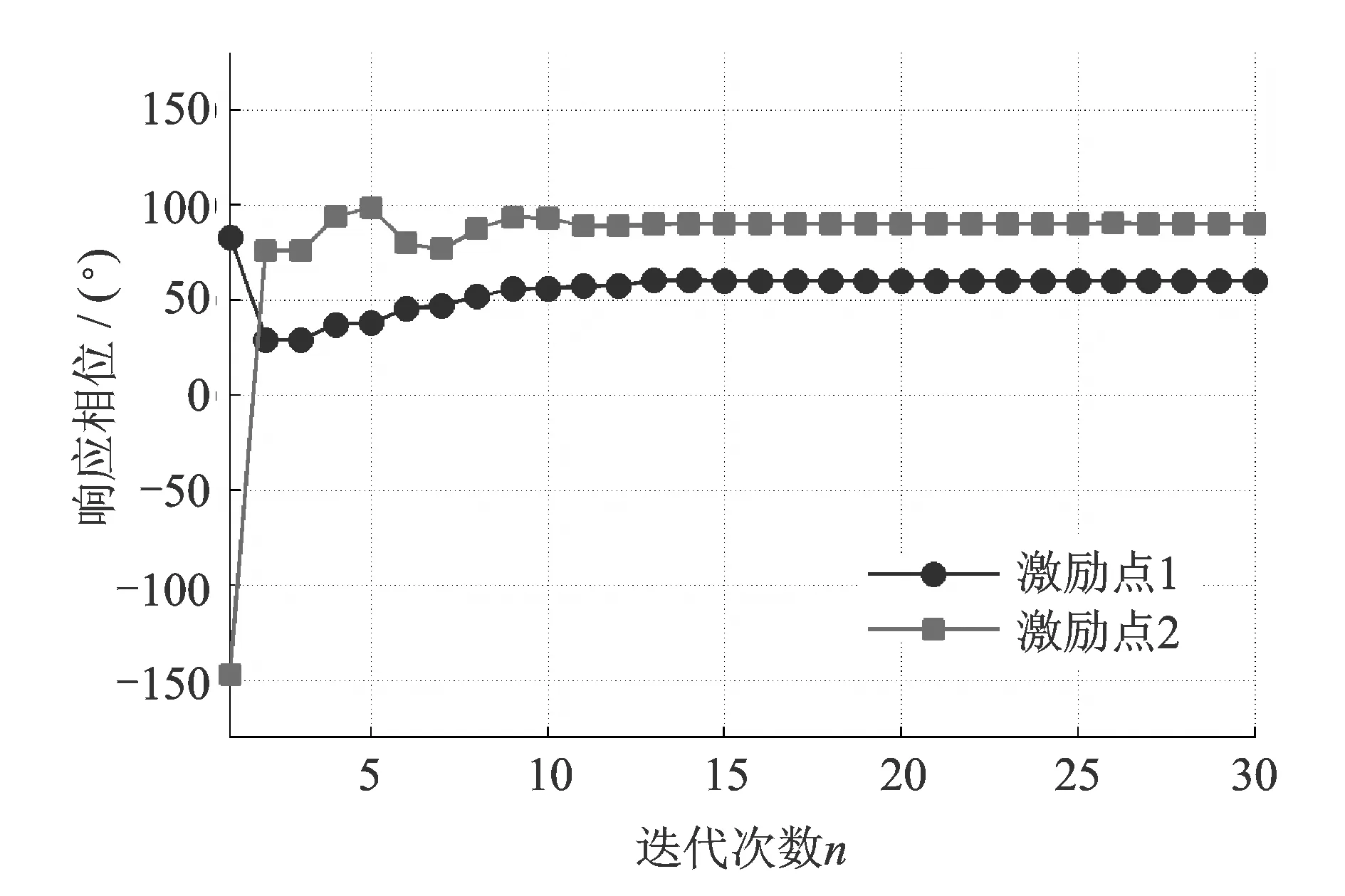
圖12 320 Hz相位響應Fig．12 Phase response at 320 Hz

接下來，控制兩振動臺在40～2000 Hz的頻率范圍內振動，激勵點1的參考幅值由上坡值(0.6～1.2g)和恒定加速度值(1.2g)組成，參考相位為60°，激勵點2的參考幅值由上坡值(0.4～1.0g)和恒定加速度值(1.0g)組成，參考相位為90°。實驗中經過30個迭代步長兩激勵點的幅值響應和相位響應分別如圖13和14所示。可以看出，兩激勵點的幅值響應在上坡段和恒定段與參考值很接近，整個頻率范圍內幅值誤差均小于0.01g，頻率范圍內兩激勵點的相位響應分別接近參考值60°和90°，誤差小于1.5°。實驗結果說明實數域控制算法在整個頻率范圍內具有良好的正弦振動控制能力。

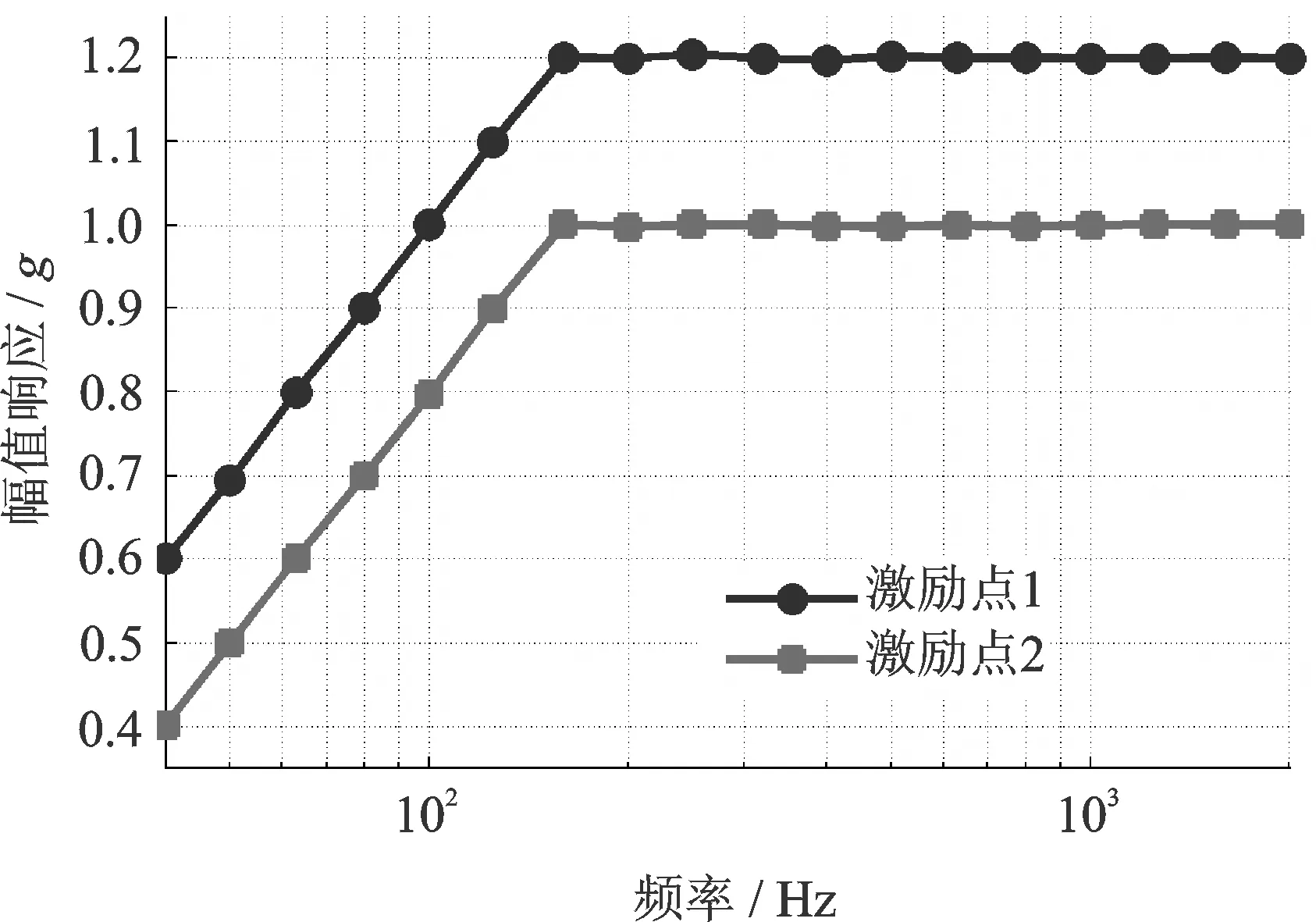
圖13 頻帶范圍內幅值響應Fig．13 Amplitude response in the frequency range

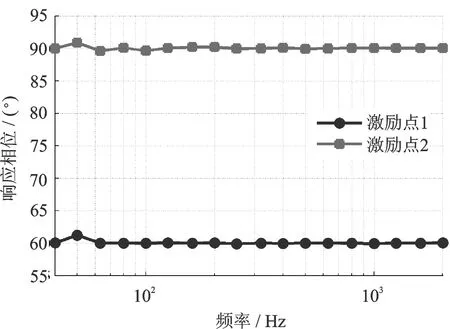
圖14 頻帶范圍內相位響應Fig．14 Phase response in the frequency range

3 結 論

本文通過建立多點激勵正弦振動控制的實數域數學模型，推導出實數形式的阻抗矩陣更新公式，并確定了最優的迭代步長，提出多點激勵正弦振動實數域控制算法的控制流程。仿真與實驗結果表明，實數域控制算法具有快速的收斂速度，能夠滿足高精度的幅值和相位響應要求，且可以有效地避免控制過程中的振蕩過沖現象。

[1] 夏益霖. 多軸振動環境試驗的技術、設備和應用[J]. 導彈與航天運載技術, 1996, (6):52—59.

Xia Y L. The technology, equipment and application of multi-axis vibration environment testing [J]. Missiles and Space Vehicles, 1996, (6):52—59.

[2] Harman C. Historical development of high performance multi-axis vibration test systems[J]. Environmental Engineering, 2004, 17(1):40—41.

[3] 陳章位, 于慧君. 振動控制技術現狀與進展[J]. 振動與沖擊, 2009, 28(3):73—77.

Chen Z W, Yu H J. Existing state and development of vibration control technology [J]. Journal of Vibration and Shock, 2009, 28(3):73—77.

[4] Stroud R C, Hamma G A, Underwood M A, et al. A review of multiaxis/multiexciter vibration technology[J]. Sound and Vibration, 1996, 30(4):20—27.

[5] 齊華. 單軸多點激勵正弦振動控制算法研究及其實現[D]. 北京：北京航空航天大學, 2001.

Qi H. The algorithm development and implementation for single-axis multi-exciter sine-wave vibration control[D]. Beijing:Beihang University, 2001.

[6] Fisher D. Theoretical and practical aspects of multiple-actuator shaker control[J]. 43rd Shock and Vibration Bulletin. 1973, 3:153—174.

[7] Hamma G A, Smith S, Stroud R C. Simulation of dynamic loads by multichannel digital control(computerized structural response prediction with application to multishaker testing)[C].Structures, Structural Dynamics and Materials Conference, 19th, Bethesda, Md. 1978: 422—430.

[8] Chen M, Wilson D. The new tri-axial shock and vibration test system at hill air force base[J]. Journal of IEST, 1989, 41(2):27—32.

[9] Flora L D, Gründling H A. Time domain sinusoidal acceleration controller for an electrodynamic shaker[J]. IET Control Theory Application, 2008, 2(12): 1044—1053.

[10]朱銀龍, 陳懷海, 賀旭東, 等. 多輸入多輸出正弦振動試驗控制系統算法研究及實現[J]. 振動工程學報, 2008, 21(1):62—65.

Zhu Y L, Chen H H, He X D, et al. Implementation of an algorithm for MIMO sinusoidal vibration test control system [J]. Journal of Vibration Engineering, 2008, 21(1):62—65.

[11]楊志東, 叢大成, 韓俊偉, 等. 基于拓展型準牛頓優化算法的單軸正弦掃頻振動控制[J]. 振動與沖擊, 2008, 27(3):99—103.

Yang Z D, Cong D C, Han J W, et al. Signle-axis swept sine vibration control using extended Quasi-Newton method [J].Journal of Vibration and Shock, 2008, 27(3):99—103.

[12]Underwood M A. Adaptive control method for multiexciter sine tests[Z]. United State Patents, 1994:5299459.

[13]Underwood M A, Keller T. Recent system developments for multi-actuator vibration control[J]. Sound and Vibration, 2001,35(10):16—23.

[14]陳家焱, 陳章位, 賀惠農, 等. 多點正弦振動試驗控制系統最優控制策略研究[J]. 機械工程學報, 2012, 48(8):159—166.

Chen J Y, Chen Z W, He H N, et al. Optimum control strategy study for multi-exciter sine test control system [J]. Journal of Mechanical Engineering, 2012, 48(8):159—166.

[15]Yamauchi Y, Uchiyama Y, Ueno K, et al. Vibration control of multi-DOF excitation systems using modern control theory. Fatigue, 2000.

[16]李慶揚, 莫孜中, 祁力群. 非線性方程組的數值解法[M]. 北京：科學出版社, 1997.

Li Q Y, Mo Z Z, Qi L Q. Numerical Method for Non-linear Systems of Equations[M]. Beijing:Science Press, 1997.

Multi-exciter sine vibration control method in the real domain

LIUZhi-hua,CAIChen-guang,YUMei,XIAYan,LIJing-sheng

(National Institute of Mechology of China, Beijing 100029， China)

Multi-exciter sine vibration system has the ability to simulate more closely approximating real-world operating conditions which contributes to achieve the vibration characteristic of the test articles. The purpose of this paper is to present the real domain control method in order to avoid complex number operations in the traditional frequency domain iterative algorithm. The real domain mathematical model of multi-exciter sine vibration control is established. Broyden’s method is formulated to deduce the real-valued impedance matrix. The iterative step used to determine the updated driving signal is optimized. On this basis, control flow to implement the real domain control method is introduced. Simulation and experiment are carried out to verify the effectiveness of the proposed control method. The results demonstrate that the real domain control method has an advantage of efficient convergence, precise response and overshoot avoidance.

vibration control; multi-exciter; Quasi-Newton method; real domain

2016-01-23；

2016-04-25

國家自然科學基金青年基金資助項目(51605461)；中國博士后科學基金資助項目(2016M591229)；公益性行業科研專項項目(201410009)

TB535

1004-4523(2016)06-1003-08

10.16385/j.cnki.issn.1004-4523.2016.06.008

劉志華(1987—),男,助理研究員。電話:15201284652；E-mail:liuzhihua@nim.ac.cn