小構(gòu)造 大智慧
——例談“特例法”在解幾何問(wèn)題中的應(yīng)用
汪麗仙
(浙江省常山縣第一中學(xué))
小構(gòu)造 大智慧
——例談“特例法”在解幾何問(wèn)題中的應(yīng)用
汪麗仙
(浙江省常山縣第一中學(xué))
俗話說(shuō):“授人以魚(yú),不如授人以漁.”然而“漁”的方式也是多種多樣的,學(xué)在平時(shí),但也只為六月試鋒,金榜題名.恰逢學(xué)校舉行了一場(chǎng)教學(xué)比武,本人選擇的課題是“特例法在解幾何問(wèn)題中的應(yīng)用”,一是出于所任教的文科班級(jí)學(xué)生基礎(chǔ)薄弱,在提升其知識(shí)掌握量及度上較困難時(shí),如何幫助他們多得分的考慮,二是想嘗試一下學(xué)生對(duì)特例法的接受及應(yīng)用程度,以便在平時(shí)的教學(xué)中加以滲透和推廣.下面就這堂課的一些教學(xué)片斷展開(kāi),談?wù)劚救说囊恍┫敕?
根據(jù)平時(shí)的教學(xué)、作業(yè)和測(cè)試,選取了學(xué)生較懼怕的平面向量運(yùn)算,并結(jié)合平時(shí)的教學(xué)進(jìn)行了選題.
問(wèn)題1:已知正方形ABCD的邊長(zhǎng)為1,點(diǎn)E是AB邊上的動(dòng)點(diǎn),則的值為.
學(xué)生2:以直線AB、AD分別為x、y軸建立平面直角坐標(biāo)系,則B(1,0),C(1,1),D(0,1),設(shè)E(x,0)

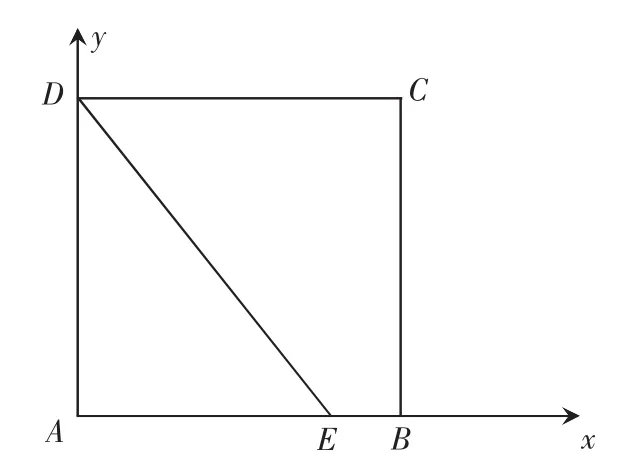
學(xué)生3:取E為AB中點(diǎn),用學(xué)生1或?qū)W生2的方式求出的結(jié)果是一樣的.筆者趁機(jī)提出“是不是可以將E點(diǎn)取得更為特殊一些呢?”
這時(shí)從學(xué)生表情上可以明顯地感覺(jué)到他們心靈的震撼.
問(wèn)題2:在△ABC中,M是BC的中點(diǎn),AM=3,BC=10,則·=______ _.

學(xué)生5:取△ABC為等腰三角形,則AM⊥BC
以M為坐標(biāo)原點(diǎn),直線MC、MA分別為x、y軸
建立平面直角坐標(biāo)系,則B(-5,0),C(5,0),A(0,3)
學(xué)生6:取△ABC為等腰三角形,則AM⊥BC
大多數(shù)學(xué)生都能想到以上的解法,轉(zhuǎn)化成學(xué)生熟悉的三角形計(jì)算問(wèn)題對(duì)多數(shù)學(xué)生來(lái)說(shuō)易接受,這也說(shuō)明了特例法具有較強(qiáng)的實(shí)用性和可操作性.
三角形中的外心、內(nèi)心、重心、垂心對(duì)很多學(xué)生來(lái)說(shuō)概念不清、易混淆,這一問(wèn)題又牽涉了向量,所以成為多數(shù)學(xué)生口中的難題.但如果從特例入手,卻有種“撥開(kāi)云霧見(jiàn)晴青天”的意境,而事實(shí)證明確實(shí)如此.此題一給出,不到3分鐘便有了回應(yīng).
學(xué)生10:取△ABC為直角三角形,則O為斜邊的中點(diǎn).若BC為斜邊,則,即P與A重合,所以P為△ABC的垂心.
這堂課是在高二學(xué)生中開(kāi)設(shè)的,選取的題目基本是高考題,但隨著課題的給出,學(xué)生處理起來(lái)游刃有余,而且積極性高漲,這足以證明特例法易被學(xué)生接受和應(yīng)用.教學(xué)比武雖然落下了帷幕,但這一方法一直延續(xù)到筆者的課堂里,而且學(xué)生受益匪淺.
例1.如下圖所示,在平行四邊形ABCD中,E為BC的中點(diǎn),F(xiàn)為CD的四分之一點(diǎn),設(shè),則m+n=______ _.
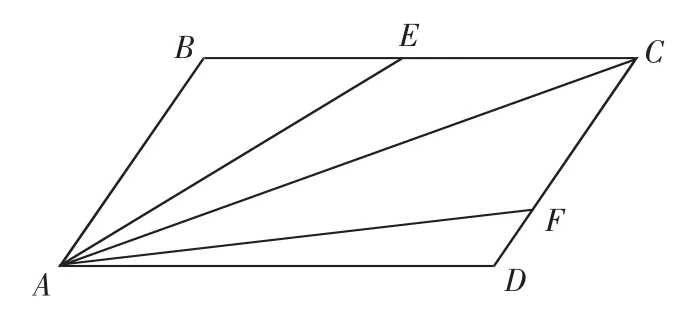
取平行四邊形ABCD為正方形,以直線AB、AD分別為x、y軸建立平面直角坐標(biāo)系,設(shè)AB=1,

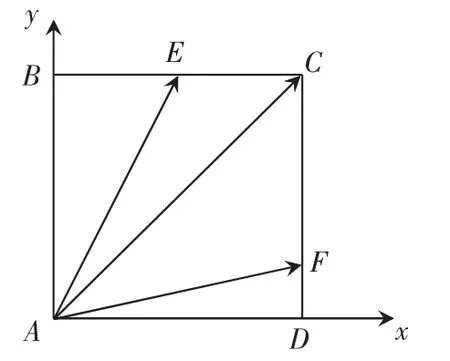
此題錯(cuò)誤率極高,原因是學(xué)生表示向量時(shí)很混亂,這一特例則省去了平面向量的表示,轉(zhuǎn)化成為坐標(biāo)的運(yùn)算,思路清晰.

這一特例的處理讓學(xué)生從復(fù)雜的設(shè)未知數(shù)運(yùn)算中得到了“解脫”.
例3.如圖,在等腰梯形ABCD中,AB∥CD且AB=2AD,設(shè)∠DAB=θ,θ∈(0,),以A、B為焦點(diǎn)且過(guò)點(diǎn)D的雙曲線的離心率為e1,以C、D為焦點(diǎn)且過(guò)點(diǎn)A的橢圓的離心率為e2,則e1·e2= _____.

此題題干讓較多學(xué)生有“暈”的感覺(jué),加之已知量少,所以運(yùn)算較難進(jìn)行,這一特例則使運(yùn)算得以開(kāi)展.
例4.在三棱錐T-ABC中,TA,TB,TC兩兩互相垂直,T在底面ABC上的正投影為D,下列命題:
①TA⊥BC,TB⊥AC,TC⊥AB;
②△ABC是銳角三角形;
其中正確的是______.(寫(xiě)出所有正確命題的編號(hào))
在正方體中取三棱錐T-ABC,則易得①②③均正確,④錯(cuò)誤.
此類題是大多數(shù)學(xué)生懼怕的題型,多選怕錯(cuò),所以很多學(xué)生寧可少選,也不多選,通過(guò)取特例建立模型既節(jié)省了時(shí)間又提高了正確率,更重要的是學(xué)生克服了恐懼敢于下手去做,提升了自信心.
諸如此類的例子舉不勝舉,可以說(shuō),學(xué)生對(duì)特例法的接受、理解、應(yīng)用程度是筆者始料不及的.作為教師,如果我們能多去觀察并了解學(xué)生的“需求”,“供應(yīng)”得恰到好處,相信我們離“供需平衡”的目標(biāo)就更近了一步.
·編輯 孫玲娟

