自適應綜合指標的化工過程參數報警閾值優化方法研究

羅 靜，胡瑾秋

自適應綜合指標的化工過程參數報警閾值優化方法研究

羅 靜，胡瑾秋*

中國石油大學(北京)機械與儲運工程學院，北京 102249

面臨日益復雜的化工過程生產裝置，提高化工過程報警系統的性能有著重要的指導意義。傳統的化工過程參數報警閾值設置方法一般只考慮誤報警，并沒有同時考慮誤報警和漏報警，導致報警系統產生大量的錯誤報警。針對上述問題，提出自適應綜合指標的報警閾值優化方法。采用核密度估計方法、基于歷史數據對過程報警狀態進行估計，綜合考慮誤報警率和漏報警率，從而建立優化報警閾值的目標函數，將數值優化算法內嵌于粒子群算法形成新的算法進行求解。案例分析中將此方法應用于TE過程，結果表明，用此方法設置的報警閾值監測誤報率為0，漏報率為0.78％。與傳統的3σ法相比，此方法能夠在保證低漏報率的條件下有效降低誤報警率，提高化工過程報警系統的性能，減輕現場操作人員的工作壓力，減少人員生命財產損失。

自適應；綜合指標；誤報警；漏報警；核密度估計；粒子群算法

0 引言

化工生產過程日益復雜，具有大量的過程數據，及時準確地判斷這些過程數據的異常狀況關乎到化工生產過程的安全性與可靠性，進而關乎到人員生命財產安全。因此，提高過程參數報警系統的性能具有重大意義。當前工業過程中存在著報警數目多的問題，根據WIT的研究[1]，操作員有效處理的報警為每天150個(每10分鐘1個報警)，一天最多處理300個報警(每5分鐘1個報警)，而在實際過程中則遠遠超出這個數字。報警數目多的直接原因是報警閾值設置的不合理，閾值范圍設置得過小會產生過多的報警，其中大部分為誤報警[2-4]。相反，如果閾值范圍設置得過大可能會漏掉重要報警，報警系統將失去作用。

常見的過程參數報警閾值的設置分為3類：(1)基于模型的方法；(2)基于知識的方法；(3)基于統計的方法。文獻[5]建立了在線和離線模型進行報警閾值的優化；文獻[6]根據數據的伯努利分布特性，在多變量統計過程中構建統計量的二級的控制限，減少了誤報警；文獻[7]將模糊神經網絡和遺傳算法用于閾值估計的訓練；文獻[8]提出核密度估計方法得到多元統計量的概率密度函數，之后由等概率密度曲線得到數據分布的正常區間。在實際工業過程中應用最多的是3σ閾值設定方法，它是根據過程參數在正常狀態的歷史數據，計算分別得到其均值μ和方差σ，將閾值范圍設在區間內。根據概率論知識，落在此區間內的概率為99.73％，而落在此范圍外的概率僅為0.27％，屬于小概率事件。然而，以上方法在設置閾值時一般只考慮誤報警，并沒有同時考慮漏報警，導致報警系統產生大量的錯誤報警。

鑒于此，提出自適應綜合指標的報警閾值優化方法。采用核密度估計方法、基于歷史數據對過程報警狀態進行估計，綜合誤報警率和漏報警率，建立優化報警閾值的目標函數，將數值優化算法內嵌于粒子群算法形成新的算法進行求解。此方法能夠有效減少誤報警和漏報警次數，提高化工過程報警系統的性能，在減少現場操作人員工作壓力的同時又能夠捕捉到重要報警信息，保證現場安全，減少人員生命財產損失。

1 自適應綜合指標報警閾值優化方法的基本概念

1.1 核密度估計

為了構造報警閾值優化的目標函數，需要利用核密度估計方法來估計過程參數的報警狀態，以確定誤報警和漏報警。核密度估計(Kernel Density Estimation, KDE)是一類基于概率密度函數的非參數估計法，它從數據樣本本身出發研究數據分布的特征。KDE基于歷史數據估計未知總體的概率密度函數，使估計的密度函數與真正的密度函數間的均方積分誤差最小。KDE的表達式為：

式中，xi為歸一化后的自變量；f(x)為自變量概率密度的估計值，取f(x)=0.99時的自變量，返歸一化后得到自變量閾值δ；r為樣本數；d為空間的維數；f(x)為核函數，本文選用高斯核函數；h為窗寬，一維最優窗寬的計算公式為

選定樣本后，根據式(1)和(2)計算每個樣本點的概率密度值，以其作為縱坐標，樣本點作為橫坐標，運用KDE方法得到過程參數概率密度函數曲線(如圖1所示)。圖中，左側曲線為正常數據分布曲線，右側曲線為異常數據分布曲線，豎線所對應的橫坐標為參數報警閾值，異常數據分布曲線下低于報警閾值部分的區域面積是漏報率的概率，正常數據分布曲線下超出報警閾值部分的區域面積是誤報率的概率。

圖1 過程參數概率密度Fig. 1 Process parameters probability density

根據最小錯誤率貝葉斯決策理論[16]，誤報警和漏報警發生的概率可以通過式(3)、(4)計算：

式中，f(x|ω1)為正常情況下的概率密度函數；f(x|ω2)為異常情況下的概率密度函數；t為報警閾值。可見，若報警閾值設置過大，誤報警的概率變小，而漏報警的概率變大；反之，誤報警的概率增大，而漏報警的概率減小。

1.2 數值優化算法

本文選用最常見的數值優化算法來尋找最佳閾值[1]。誤報警和漏報警均屬于錯誤報警，因此，將錯誤報警率作為數值優化算法的目標函數，建立如下報警閾值優化問題

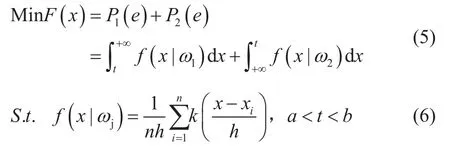
式中，f(x)是錯誤報警率；P1(e)是誤報警率；P2(e)是漏報警率；t是選擇的閾值；n是樣本點個數；h是KDE的窗寬，由式(2)計算。

數值優化算法的實現步驟如下：

(1)在區間[a,b]，構造兩點x1=a+q(b-a )，x2=a+(1-q)(b-a )，式中，q和(1-q)分別是算法的兩個系數一般取q=0.382；

(2)若F(x1)＜F(x2)，則搜索區間縮小為[a,x2]， b=x2，判斷是否成立，如果成立轉到步驟(4)，否則返回步驟(1)；

(3)若F(x1)≥F(x2)，則搜索區間縮小為[x1,b]， a=x1，判斷是否成立，如果成立轉到步驟(4)，否則返回步驟(1)；

然而，數值優化算法的系數q和(1-q)是人為設置的，并不能保證算法尋優結果接近全局最優。因此，本文采用粒子群(Particle Swarm Optimization, PSO)算法對系數q進行優化，使尋優結果接近全局最優。

1.3 粒子群算法

粒子群(PSO)算法最早在1995年被提出，是一種從生物活動中得到啟發而模擬自然界生物集群現象的進化算法。在PSO算法中，每個優化問題的潛在解都稱為“粒子”，所有的粒子都有一個由被優化的函數決定的適應值(Fitness Value)，每個粒子還有一個速度決定它們移動的方向和每一步的位移。然后粒子們就追隨當前的最優粒子在解空間中搜索。PSO算法需要初始化一群隨機粒子(隨機解)，然后通過迭代找到最優解，在每一次迭代中，粒子通過跟蹤兩個“極值”來更新自己。第一個就是粒子本身所找到的最優解，這個解稱為個體極值。另一個是整個種群目前找到的最優解，這個解稱為全局極值。

假設在一個N維的目標搜索空間中，有m個粒子組成一個群落，將第i個粒子的位置表示為一個N維的向量，記為每一個粒子都是潛在的解，將帶入一個目標函數就可以計算出其適應值，根據適應值大小衡量的優劣。第i個粒子的移動速度也是一個N維的向量，記為速度決定粒子在搜索空間單位迭代次數的位移。記第i個粒子迄今為止搜索到的最優位置為整個粒子群迄今為止搜索到的最優位置為粒子根據以下公式來更新其速度和位置

式中，i=1,2,…,m ；n=1,2,…,N；速度權重w隨機取值于[-1,1]；學習因子c1和c2是非負常數；r1和r2是介于[0,1]之間的隨機數；vin是第i個粒子速度向量的第n維是常數，根據實際情況設定。

迭代終止條件一般選為最大迭代次數或粒子群迄今為止搜索到的最優化位置滿足適應閾值。因為是整個粒子群的最優值，因此上述PSO算法也稱為全局PSO算法。

2 自適應綜合指標報警閾值優化方法步驟

針對傳統閾值優化方法僅考慮誤報警，并沒有綜合考慮誤報警和漏報警從而造成大量漏報的問題，提出自適應綜合指標報警閾值優化方法。綜合考慮誤報警和漏報警兩個方面建立目標函數，并用數值優化算法內嵌入PSO算法形成新的算法對報警閾值尋優，力求達到降低錯誤報警次數的目的，從而減輕現場操作人員的工作壓力。自適應綜合指標報警閾值優化方法的工作流程如圖2所示，具體步驟如下：

步驟1：選擇化工過程某參數的正常樣本X∈R1×NS和故障樣本Y∈R1×NS。其中，NS是樣本點個數，根據實際情況選取；

步驟2：繪制概率密度曲線，設置解區間。基于數據樣本X和Y，利用式(1)和(2)分別估算過程參數正常條件下和故障條件下的概率密度，以其作為縱坐標，樣本點作為橫坐標，繪制過程參數概率密度曲線，并設置解的區間[a,b]。若求報警閾值上限的區間，a=max(X )-3σ，b=max(X )+3σ；若求報警閾值下限的區間，a=min(X)-3σ，b=min(X)+3σ。式中，σ為正常樣本X的標準差；

步驟4：設置PSO算法的參數。粒子速度的慣性權重w隨機取值于[-1,1]；粒子速度的最大值vmax=0.5；粒子個體最優的學習因子c1=cθ1，其中，c=(2w+2)θ2，θ1和θ2均隨機取值于[0,1]；粒子群體最優的學習因子c2=c-c1；算法最大迭代次數M=200；種群個體數目m=50；算法精度e=0.000 1。

步驟5：初始化粒子的位置和速度。用系數iq對應的一維向量來標記第i個粒子在一維搜索空間中的位置。第i個粒子的移動速度也是一個一維的向量，記為設置第i個粒子的初始位置粒子的初始速度其中，3θ和4θ均是隨機取值于[0,1]的值。此時，記粒子代數1k=。

步驟7：粒子的位置和速度的更新。1kk=+，根據式(5)計算第i個粒子更新后的速度判斷當代第i個粒子的速度是否成立：1)若成立，令若不成立，判斷是否成立，若成立，令若不成立，根據式(6)計算第i個粒子更新后的位置使得

3 實例分析

3.1 TE過程

由伊斯曼公司設計的TE(Tennessee Eastman)過程是一個基于實際工業過程的仿真平臺，共包含了反應器、冷凝器、壓縮機、分離器和汽提塔等5個操作單元，涉及到12個操作變量和41個測量變量。TE過程的工藝流程圖如圖3所示，部分測量變量如表1所示。

3.2 閾值監測

以反應堆溫度為例，用自適應綜合指標的化工過程參數報警閾值優化方法設置變量閾值，進行溫度監測。與化工生產中常見的3σ法進行對比，證明該方法能夠降低錯誤報警率，優化報警系統的性能。

3.2.1 自適應綜合指標報警閾值優化方法

選擇TE過程反應堆溫度測量變量作為研究對象，運行過程512時刻，在第256時刻加入干擾，使反應堆冷卻水閥粘滯，前256時刻過程為正常狀態，后256時刻過程為故障狀態。選取反應堆溫度前256組數據作為正常訓練樣本X∈R1×256，后256組數據作為故障訓練樣本Y∈R1×256。保持同樣的操作條件，運行過程256時刻，在第161時刻加入同樣的干擾，獲得測試樣本Z∈R1×256(反應堆溫度曲線如圖4所示)；

根據數據訓練樣本X和Y，采用式(2)計算得反應堆溫度正常數據核密度估計的窗寬h1=0.382 8，反應堆溫度故障數據核密度估計的窗寬h2=0.729 9。根據式(2)分別估算反應堆溫度正常條件下和故障條件下的概率密度，以其作為縱坐標，樣本點作為橫坐標，繪制反應堆溫度的概率密度曲線(如圖5所示)。分別設置閾值上限的取值區間[120.449 2,120.450 8]和閾值下限的取值區間[120.349 2,120.350 8]；

其中，F1(x)和F2(x)是錯誤報警率，t1和t2是選擇的閾值，KDE窗寬h1=0.382 8，h2=0.729 9。

運行報警閾值優化算法：

(1)報警閾值上限優化

圖2 自適應綜合指標報警閾值優化方法步驟Fig. 2 Steps of the adaptive composite-indicator alarm threshold optimization method

圖3 TE工藝流程圖Fig. 3 Flowchart of the tennessee eastman process

表1 部分TE過程測量變量表Table 1 Part of TE process measured variables

設置PSO的參數：粒子速度的慣性權重w=0.909 6，粒子速度的最大值vmax=0.5，粒子個體最優的學習因子c1=0.562 3，粒子群體最優的學習因子c2=0.561 9，算法最大迭代次數M=200，種群個體數目m=50，算法精度e=0.000 1。

調用閾值優化算法進行迭代計算，算法共運行5次，輸出最優報警閾值上限t1=120.450 3，最優數值優化算法參數q1=0.005 6，適應度G(q1)=0.001 0。

(2)報警閾值下限優化

設置PSO的參數：粒子速度的慣性權重w=-0.341 0，粒子速度的最大值vmax=0.5，粒子個體最優的學習因子c1=0.022 0，粒子群體最優的學習因子c2=0.380 5，算法最大迭代次數M=200，種群個體數目m=50，算法精度e=0.000 1。

圖4 反應堆溫度曲線Fig. 4 Reactor temperature curve

圖5 反應堆溫度的概率密度曲線Fig. 5 The probability density curve of reactor temperature

調用閾值優化算法進行迭代計算，算法共運行6次，輸出最優報警閾值下限t2=120.350 3，最優數值優化算法參數q2= 0.010 1，適應度G(q2)= 0.001 0。

用最優的報警閾值[120.350 3,120.450 3]對反應堆溫度測試數據Z進行監測，監測結果如圖6所示

圖6 自適應綜合指標法監測結果Fig. 6 Monitoring results of the adaptive comprehensive-index method

3.2.2 3σ法

計算反應堆溫度正常樣本X均值μ=120.400 4，標準差σ=3.533 3e-3。由3σ法求得報警閾值[μ-3σ,μ+3?]=[120.390 0,120.411 2]，并用該閾值對測試數據Z進行監測，監測結果如圖7所示。

3.3 結果對比

自適應綜合指標報警閾值優化方法與3σ法的誤報警和漏報警情況對比如下：

由表2可知，與3σ法相比，自適應綜合指標報警閾值優化方法所設閾值誤報警率降低了51.95％，漏報警率僅為0.78％，接近于0，誤報警和漏報警次數之和減少131次，證明該方法可以有效減少誤報警次數，提高報警系統性能，減少操作人員工作壓力。

4 結論

(1)傳統的化工過程參數報警閾值設置方法一般只考慮誤報警，并沒有同時考慮誤報警和漏報警這兩個問題，導致報警系統產生大量的錯誤報警。針對這個問題，提出自適應綜合指標的報警閾值優化方法。該方法采用核密度估計方法、基于歷史數據對過程報警狀態進行估計，綜合誤報警率和漏報警率，從而建立優化報警閾值的目標函數，并創新地將數值優化算法內嵌于粒子群算法形成新的算法進行求解。

(2)案例分析中，將新方法應用于TE過程的反應堆溫度監測，分別優化報警閾值上下限，并進行閾值監測。

圖7 3σ法監測結果Fig. 7 Monitoring results of the 3σ method

表2 TE過程反應堆溫度監測的誤報次數和漏報次數Table 2 The number of false positives and false negatives of TE process reactor temperature monitoring

(3)自適應綜合指標報警閾值優化方法所求的報警閾值監測誤報率為0，漏報率為0.78％。與傳統的3σ法相比，此方法能夠在保證低漏報率的條件下有效降低誤報警率，提高化工過程報警系統的性能，減輕現場操作人員的工作壓力，減少人員生命財產損失。

[1]WIT J D.EEMUA recommendations for the design and construction of refrigerated liquefed gas storage tanks[J].Cryogenics, 1998, 28(12):800-804.

[2]FOONG O M, SUZIAH, ROHAYA D, et al. ALAP: Alarm prioritization system for oil refnery[J].Proceedings of the World Congresson Engineering and Computer Science, 2009, (2):1012-1017.

[3]CHAO C S, LIU A C. An alarm management framework for automated network fault identifcation[J].Computer Communications, 2004, 27(13):1341-1353.

[4]EBERHART R C, KENNEDY J.A new optimizer using particle swarm theory[C]. Sixth International Symposium on Micro and Human Science, 4-6 Oct.1995, (2): 39-43.

[5]JIANG R. Optimization of alarm threshold and sequential inspection scheme[J].Reliability Engineering and System Safety, 2010, 95:208-215.

[6]CHEN T. On reducing false alarms in multivariate statistical process control[J].Chemical Engineering Research and Design, 2010, 88(4): 430-436.

[7]MEZACHE A, SOLTANI F.A novel threshold optimization of ML-CFAR detector in Weibull clutter using fuzzy-neural networks[J]. Signal Processing, 2007, 87:2100-2110.

[8]MARTIN E B, MORRIS A J. Non-parametric confdence bounds for process performance monitoring charts[J].Process Control, 1996, 6(6):349-358.

A study of adaptive composite-indicator alarm threshold optimization of chemical process parameters

LUO Jing, HU Jinqiu
School of Mechanical & Storage and Transportation Engineering, China University of Petroleum-Beijing, Beijing 102249, China

Faced with increasingly complex chemical process plants, improving the performance of chemical process alarm systems is important. The traditional chemical process parameters alarm threshold setting method generally considers only false positives, but not taking both false positives and false negatives into account, leading to a lot of false alarms in alarm systems. To solve these problems, we used the alarm threshold optimization method based on an adaptive composite indicator. We used the kernel density estimation method to estimate the state of the process alarm based on historical data, integrating the false positives rate and false negatives rate to establish an objective function for optimal alarm thresholds. The numerical optimization algorithm was embedded in a particle swarm optimization algorithm, forming a new algorithm to solve the function. In case, this method was applied to the TE process. The results showed a false positive rate of 0, and a false negative rate of 0.78％. Compared with the traditional 3σ method, this method can effectively reduce the rate of false positives with a low false negative rate, and improve the performance of the chemical process alarm system. This will reduce stress on site operators, as well as the risks of loss of life and property.

adaptive; composite-indicator; false positives; false negatives; kernel density estimation; particle swarm optimization algorithm

2016-11-15

10.3969/j.issn.2096-1693.2016.03.036

(編輯 付娟娟)

羅靜, 胡瑾秋. 自適應綜合指標的化工過程參數報警閾值優化方法研究. 石油科學通報, 2016, 03: 407-416

LUO Jing, HU Jinqiu. A study of adaptive composite-indicator alarm threshold optimization of chemical process parameters. Petroleum Science Bulletin, 2016, 03: 407-416. doi: 10.3969/j.issn.2096-1693.2016.03.036

*通信作者, hujq@cup.edu.cn