導航過程中最短路徑的動態調整算法

趙忠孝，馮嫻

(1.福州外語外貿學院 信息系，福建 福州 350202; 2.福建工程學院 軟件學院，福建 福州 350003)

導航過程中最短路徑的動態調整算法

趙忠孝1，馮嫻2

(1.福州外語外貿學院 信息系，福建 福州 350202; 2.福建工程學院 軟件學院，福建 福州 350003)

在導航過程中，當最短路徑道路上有擁擠、堵塞或中斷的情況發生時，利用Dijkstra最短路徑算法中的最短路徑長度和前驅結點兩個輔助向量數據，可迅速在其鄰接結點中選擇一條新的最短路徑。實現了最短路徑的動態調整，從而可以盡快地到達目的地。

導航; 圖論; 最短路徑; Dijkstra

最短路徑問題是圖論中的一個經典課題，在各種導航系統中有廣泛的應用。最短路徑算法有距離、時間和經濟效益等多種判斷標準，一般僅以時間花費作為判斷最短路徑的標準。最短路徑算法分靜態最短路徑和動態最短路徑算法。Dijkstra等傳統的最短路徑算法屬靜態最短路徑算法，其研究已經比較成熟，動態最短路徑算法成為近期研究的熱點。在動態最短路徑算法中，有限定搜索區域的算法[1]，也有限定搜索方向的A*算法[2-5]，其基本思路是縮小搜索的范圍，提高了搜索效率。這些算法都是在路徑參數動態變化的情形下重新搜索最短路徑，忽略了由靜態算法搜索最短路徑時所生成的相關數據。現有的動態最短路徑的算法都是根據路徑中變化權值，重新搜索最短路徑，其時間花費均在O(N2)之上。實際上，在導航開始時已經搜索到一條最短路徑，并有最短路徑長度和前驅結點兩個輔助向量的數據。在導航的過程中，只是在最短路徑上發生了擁擠、堵塞或中斷。此時，并不需要在整個路網中重新搜索，完全可以利用已有的數據，對部分路徑進行一些小范圍的調整，便可迅速選擇一條新的最短路徑。

1 相關概念

Dijkstra 最短路經算法是計算帶權有向圖從源點V0到其他各點的最短路徑，按路徑長度的遞增次序，逐步產生 “貪心”(Greedy)的算法。為方便，本文僅以無向圖為例進行討論。實際上，交通線路等大多數是無向圖。對于有向圖，若某弧不存在，則可認為其對應的邊不存在即可。下面先介紹該最短路徑算法中用到的相關概念。

1.1 定義

設有向圖G=(V,E),給定結點v1,v2,…，vn∈V, 邊e1,e2,…，em∈E,用鄰接矩陣C表示有向圖G，權C[i][j]定義為：

其中，wij表示邊(vi,vj)上權值，∞表示一個計算機允許的、大大大于所有邊上權值的數。

1.2 相關的數據結構

用C語言定義的數據結構：

#define MaxVertexNum 100

∥*最大頂點數設為100

#define MAX 90 000.0

∥*設定最大權值為90 000.0

typedef char VertexType;∥*頂點類型設為字符型

typedef float EdgeType; ∥*邊的權值設為實型

typedef struct

{VertexType vexs[MaxVertexNum];∥*頂點表

EdgeType

edges[MaxVertexNum][MaxVertexNum]; ∥*鄰接矩陣，即邊表

int n,e; ∥*頂點數和邊數

}MGraph;

intP[N];

floatD[N];

MGraph *G。

(1)用鄰接矩陣來表示帶權無向圖(圖1)。

(2)輔助向量floatD[N]用來存儲源點到其余各結點的最短路徑長度。

(3)輔助向量floatP[N]用來存儲源點到其余各結點的最短路徑上前驅結點。

圖1有11個結點，圖中的數值表示其對應邊上的權值，其鄰接矩陣如圖2所示。

由Dijkstra最短路徑算法，能夠計算出從一個結點到其他結點的最短路徑。比如，從V0到其他結點的最短路徑。在圖3中，V0到各結點的實線路徑為最短路徑，虛線為原來邊。這樣，V0到V6的最短路徑為：V0→V2→V5→V6。V0到V10的最短路徑為：V0→V2→V5→V7→V10。由于是無向圖，從V10到V0的最短路徑應該是相反的一條路徑V10→V7→V5→V2→V0，其長度是一樣的。在這條路徑上，稱路徑上將要到達的結點為前驅結點，如V7是V10的前驅結點，V5是V7的前驅結點等。

圖1 有權無向圖Fig.1 Weighted undirected graph

圖2 鄰接矩陣

Fig.2 Adjacency matrix

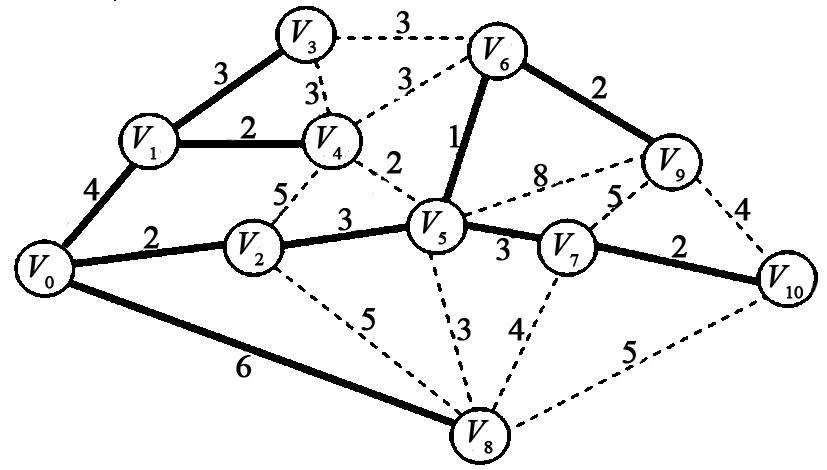
圖3 最短路徑圖Fig.3 The shortest path graph

在Dijkstra算法結束時，各結點到V0最短路徑長度存儲在輔助向量D[N]中。具體數值如表1所示。

表1 各結點到V0的最短路徑值Tab.1 The shortest path value of each node to V0

各結點到V0的最短路徑上的前驅結點存儲在輔助向量P[N]中。具體數值如表2所示：

表2 各結點到V0的最短路徑的前驅結點

Tab.2 The precursor nodes of the shortest path of each node toV0

結點012345678910前驅00011255067

若現在從V10沿著最短路徑向V0行駛，當行使到V5時發現V5-V2的道路堵塞或中斷。此時，如何迅速地重新選擇一條新的最短路徑，就是一個迫切需要解決的問題。

2 算法思想

如果V5-V2之間的道路堵塞或中斷，則其對應邊上的權值就會增大。例如：w25=3變成w’25=7，其增值為4,用w=4來表示。這樣原來最短路徑值也隨之發生改變，改變后的值用D’[5]表示：

D’[5]=D[5]-w25+w’25=5-3+7=9

從V5到V0的最短路徑長度由5變成了9。這樣，原來的最短路徑可能已經不是最短路徑了，需要重新計算來確定一條新的最短路徑。從V5出發到V0的最短路徑一定是經過V5鄰接點的一條路徑，V5鄰接點有V2、V4、V6、V7、V8和V9。這些鄰接點到V0都是已經有最短路徑，現只需要從V5經過其鄰接點到V0的所有可能的最短路徑中選擇一條最短的路徑即可。也就是：

D’[5]=MIN{(D[i]+w5i) |Vi∈V5的鄰接結點}。

現可將V5的鄰接結點劃分為兩個集合，分別命名為S1和S2。其中S1的結點是其到V0的最短路徑不經過V5的結點，如V2、V4、V8等結點。S2的結點是其到V0的最短路徑經過V5的結點，如V6、V7等結點。對于S1中的結點，V5經過各結點的最短路徑的值計算如下：

D[2]+w52=2+7=9,

D[4]+w54=6+2=8,

D[8]+w58=6+3=9,

其中最小的值為8,是經過V4的一條路徑的值，用min1=8表示。但還不能確定min1=8就是最短路徑的值，還需要和S2中結點的最短路徑進行比較。由于S2中結點的最短路徑也走V5-V2這條邊，其原最短路徑的值自然也會增大，也需要重新確定一條最短路徑。對于Vi∈S2，如果D[i]+w5i的值已經大于min1, 則可以排除在外。如：D[7]+w57=8+3=11,新的最短路徑值一定不會大于min1，可以排除經過此結點為最短路徑經過的結點。而對于V6來說，D[6]+w56=6+1=7,其值雖小于min1，但其原來最短路徑經過V5，V6原來的最短路徑也可能已經不是最短路徑了。其最短路徑的值也還不能直接確定，需要用相同的方法，也就是遞歸算法來確定V6最短路徑的值。如果V6鄰接點中仍有結點最短路徑經過當前結點，仍需要繼續遞歸，直到沒有鄰接點的最短路徑經過當前結點為止。

為不失一般性，設發生堵塞或中斷的結點為Vk，也就是要調整從Vk到V0的最短路徑。由于各結點最短路徑的前驅結點存儲在向量P[N]中，若P[i]=k,則鄰接點Vi到V0的最短路徑直接經過結點k，否則沒有經過。Vk鄰接點則是鄰接矩陣k行中對應值小于∞的那些結點。其算法形式化描述如下：

dynamicshort(MGraph *G,intk,floatw)

∥*G為帶權有向圖，k為當前結點，w為路徑的增值

{D[k]=D[k]+w; ∥* 修改當前結點到V0的路徑長度

min1=D[k];

i=0;

{ min1=min{D[i]+G->edges[k][i]|Vi∈s1}; ∥*s1為最短路徑不過Vk的結點集

}

i=0;

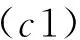
{ if(min1>D[i]+G->edges[k][i])

dynamicshort (G,i,w);

if(min1>D[i]+G->edges[k][i])

∥*判斷新路徑是否為最短路徑，若是則修改最小值，并記下當前結點。

{ min1=D[i]+G->edges[k][i];

p1=i++;

}

}

P[k]=p1; ∥*修改當前結點的前驅結點

D[k]=min1;∥*修改最短路徑長度

return;

}。

3 算法分析

由Dijkstra等單源最短路徑算法的結果，是生成以單源結點為根的一顆樹。各結點走向樹根的路徑就是其最短路徑。在前進方向上堵塞或中斷時，僅需要從其鄰接結點尋找最短路徑。一般情況下，道路的鄰接矩陣是一個稀疏矩陣，每個點的鄰接點的數量也十分有限，會大大小于網絡總的結點數。在鄰接點中，S1中的結點數N1一般應大于S2的結點數N2。對S1中的結點，只需要N1檢索。對于N2中的結點，若min1是已經找到的最短路徑的值，對于原最短路徑大于該值的，不需要進一步再判定。只需要將那些原來的最短路徑值小于min1的結點遞歸調用本算法。且每遞歸一次，其最短路徑的值都在增加，若其值超過min1則終止。因最短路徑是一個樹型結構，遞歸調用到葉結點將會終止。因此，遞歸調用的層次也是非常有限的。本文對有20個結點的網絡中的每個結點進行了最短路徑調整的測試。每次測試時，將結點與其前驅結點的邊值增加一個隨機值。使其原來的最短路徑發生了改變，統計了各結點搜索新的最短路徑其循環次數c1(在算法已有標示)和最短路徑值的修改次數c2(在算法已有標示)。各結點搜索次數的具體結果見表3。

表3 各結點搜索次數統計Tab.3 Each node search statistics

對這20個結點的網絡利用本算法，使改變的路徑調整到最短路徑只需要平均49.5次循環，對最短路徑的值進行了2.6次修改。其總的時間復雜度一般不會超過O(n)。若用Dijkstra最短路徑算法進行搜索，則需要760次循環，最短路徑的值也要進行76次修改運算。

4 結束語

在文獻[2]中，證明了動態網絡的最短路徑是一個NP完全問題，將動態問題化為若干個時間段，分段是穩定的。每個穩定區間都要解不等式組，迭代次數為k，k為子區間數。依次將每一個穩定區間的解連接起來得到整體的解。其初始要調用Dijkstra算法，算法復雜度為O(n2)，各子區間算法的時間復雜度為O(mK)，K=max(n,k)。文獻[3]中算法的時間復雜度比Dijkstra算法僅快1～2倍。其他文獻所給出算法的復雜度都在O(n2)附近，本算法的時間復雜度遠遠低于已有的算法。在遇到堵塞或中斷事件后，可利用本算法迅速找到另一條到達目的地的最短路徑。

[1]汪曉潔,湯建國，李娟，等.基于可變權值的態最短路徑算法[J].新疆大學學報(自然科學版)，2015，32(3)：342-346.

[2]林瀾,閆春綱,蔣昌俊，等.動態網絡最短路問題的復雜性與近似算法[J].計算機學報,2007,30(4)：608-614.

[3]鄒亮,徐建閩,朱鈴湘.A_算法改進及其在動態最短路徑問題中的應用[J].深圳大學學報(理工版),2007，24(1)：32-35.

[4]周琳，陳發鋼.車載導航系統中動態最短路徑研究[J].牡丹江師范學院學報(自然科學版),2013(3):23-25.

[5]章昭輝.一種基于離散變權網絡的動態最短路徑快速算法[J].計算機科學,2010，37(4)：238-240.

[6]張一珂，劉鴻劍，朱志斌,等.基于車輛導航的一種改良動態最短路徑算法[J].科技廣場,2009(5)：26-28.

[7]任子輝，王堅.緊急事件的動態交通流模型及雙向動態最短路誘導算法[J].計算機應用,2008，28(11)：2955-2960.

[8]陳曉紅，王艷娟.改進的Dijkstra算法在動態路徑引導中的實現[J].科學技術與工程,2008，8(22)：6024-6027.

[9]田鵬飛，王劍英.動態最短路徑算法及其仿真 [J].計算機仿真,2007，24(6)：153-155.

[10]Huang A B, Wu B Q, Zhan F B. A shortest path algorithm with novel heuristics for dynamic transportation networks[J]. Intenational Journal of Geographical Information Science,2007(6)：625-644.

[11]Chabini I, Lan S. Adaptations of the A* algorithm for the computation of fastest in deterministic discrete time dynamic networks[J]. IEEE Transactions on Intelligent Transportation Systems,2002,3(1):60-74.

[12]SharmaY, Saini S C, Bhandhari M. Comparison of dijkstra shortest path algorithm with genetic algorithm for static and dynamic routing network[J]. International Journal of Electronics and Computer Science Engineering,2012,1(2):516-525.

(特約編輯：黃家瑜)

A dynamic alignment algorithm for the shortest path in the navigation process

Zhao Zhongxiao, Feng Xian

(1. Information Department, Fuzhou College of Internation Studies and Trade，Fuzhou 350202，China;2. Software College, Fujian University of Technology, Fuzhou 350003, China)

The distance (length) of the shortest path and the data of two supplementary vectors of the previous nodes were adopted to quickly generate an alternative shortest path from adjacency nodes via Dijkstra algorithm. The dynamic alignment of the shortest path in navigation process was implemented to reach the destination in prompt moment.

navigation； graph theory； shortest path； Dijkstra

2016-06-27

趙忠孝(1948- )，男，山西聞喜人，教授,研究方向：算法設計與分析、數據庫設計。

10.3969/j.issn.1672-4348.2016.06.006

TP301

A

1672-4348(2016)06-0543-04