自平衡機器人中數據融合算法的研究與實現

呂傳龍，曹華杰，劉浩東

(1.西南交通大學 電氣工程學院，四川 成都 610031;2.西南交通大學 信息科學與技術學院，四川 成都 611756)

自平衡機器人中數據融合算法的研究與實現

呂傳龍1，曹華杰2，劉浩東1

(1.西南交通大學 電氣工程學院，四川 成都 610031;2.西南交通大學 信息科學與技術學院，四川 成都 611756)

輪式自平衡機器人是一種通用的機器人，它適用于各種復雜環境中，通過陀螺儀和加速度計采集的數據可以控制其平衡性，但是不夠精確和實時。為了進一步提高系統的響應，文中通過離散卡爾曼算法將ENC03陀螺儀和MMA7260加速度計采集的數據進行融合輸出。首先研究了傳統的卡爾曼算法，然后建立了適合自平衡機器人的算法模型，最后介紹了其工程實現。通過實時監測可以看出，在未進行角度融合之前，加速度計計算得出的角度在靜態和動態都有著極大的噪聲。經過卡爾曼濾波算法融合后的角度平滑穩定，達到了預期效果。

自平衡機器人；加速度計；陀螺儀；卡爾曼算法；數據融合

0 引 言

輪式自平衡機器人是控制科學的一個重要研究平臺，同時也是實際應用的重要工具。20世紀90年代，日本開展了平衡機器人的相關研究，為后來的移動平衡機器人學建立了相關研究基礎。21世紀初，自平衡機器人得到了越來越多的關注，國外高校逐漸采用其作為先進理論的驗證平臺，機器人公司也開始將輪式自平衡機器人進行商業化。比如，美國公司賽格威研究開發兩輪自平衡代步車，除了已經在個人用戶的使用上得到推廣外，在機場、高檔社區和運動場館等大型空間內也得到使用。近年來，越來越多的互聯網公司加入平衡機器人的開發中，對平衡機器人的推廣普及有著深刻影響。

1 傳感器數據采集

輪式自平衡機器人的穩定運行建立在正確獲得其姿態信息的基礎上，通過一定的控制算法驅動電機保持平衡穩定狀態。其姿態信息主要是指在靜止或者平衡狀態下，機器人重心與豎直方向的傾角。機器人姿態的信息需要兼顧其動態特性和靜態精度，傾角測量需要滿足動態與靜態性能指標。靜態指標是指在穩定狀態下可以長時間正確表示實際觀察量；動態指標是指當測量的物理量在高速運動狀態下，仍可以快速跟隨狀態變化，并且具有一定的預測性。為了得到機器人的復合要求的姿態傾角，可以采用陀螺儀的角速度動態特性和加速度計的靜態精度相結合的方法[1]。

陀螺儀是一種利用科里奧利力原理，對旋轉物體測量其角速度的元件。陀螺儀適應于系統運動時的角速度信息，對其積分可以得到實際運動中的傾角。然而，受到陀螺漂移等因素的影響，產生的微小誤差經過積分作用之后，會使測量的角度產生巨大的偏差。因此，應對的主要是陀螺漂移的低頻噪聲[2]。為此，需要設計濾波電路對陀螺儀輸出信號進行濾波，將低頻噪聲濾除，同時要保證系統高頻信號不能達到陀螺儀的共振頻率。

加速度計是一種測量重力加速度分量以及運動加速度的元件。對于輪式自平衡機器人，利用加速度計元件測量重力加速度分量，進行反三角函數運算得到機器人重心與豎直方向的夾角，作為機器人車體的傾角。加速度計在運行中易受到平臺震動這樣的高頻噪聲的影響。設計中采用飛思卡爾半導體公司出品的加速度計MMA7260。根據公式可以推導出傾角的變化量：

Δu=kgsinθ

(1)

其中，u是加速度計輸出電壓值；g是重力加速度；θ是車模傾角；k是比例系數。

2 卡爾曼數據算法融合研究

得到機器人的姿態信息是平衡車系統最具挑戰的部分之一。陀螺儀和加速度計分別為不同的角度傳感器，在該系統中采用雙傳感器進行角度測量。然而，加速度計容易受到自身器件的噪聲、電機噪聲以及陀螺儀混疊的影響，而且在高速運動的體系下具有嚴重的滯后特性；陀螺儀噪聲小，但是存在著溫度漂移現象，靜態性能不足以達到要求。為了保留加速度計的靜態性能和陀螺儀的動態性能，使兩者優勢可以相互結合，文中采用多傳感器信息融合算法中的濾波器融合算法[3]。

典型的數據融合算法大致分為兩類：一類是從頻率域來分辨、消除噪聲，不考慮信號及噪聲的統計特性，例如互補濾波器[4]；另一類是使用狀態空間法在時域內設計濾波器，例如卡爾曼濾波器[5]。互補濾波的基本思想是通過不同傳感器具有互補作用的特性進行角度融合。對于輪式機器人采用互補濾波的方式進行濾波，需要實時地將時域信息轉換到頻域空間，在頻域中設計針對陀螺儀和加速度計的濾波器，最后進行互補融合。

針對上述所選濾波器進行如下設計：利用高通濾波器抑制陀螺儀積分的漂移，利用低通濾波器濾除加速度計的短時性快速變化的信號，將處理后的數據進行融合以得到小車的實際傾角。最后將加速度濾波和陀螺儀濾波的角度各乘以一個權重，其權重和為1即可[6]。其濾波過程如圖1所示。然而在復雜的情況下，濾波器的帶寬難以動態選擇，這給互補濾波器的設計帶來了困難。

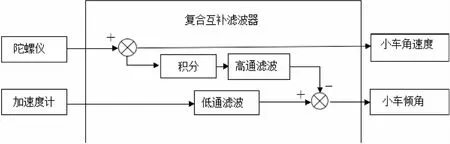
圖1 復合互補濾波器

相對于其他濾波方式，卡爾曼濾波有著諸多優點：采用狀態空間法設計濾波器，用狀態方程表征系統的運動特性，從而避免了在頻域中討論和設計濾波器的繁瑣，簡單易行[7]；在遞推運算中，實時量測信息經提煉被濃縮在估計值中，而不必存儲時間過程中的量測量[8]。所以，卡爾曼濾波能適用于白噪聲激勵的任何平穩或非平穩隨機向量過程的估計，所得估計在線性估計中精度最佳。

2.1 卡爾曼濾波算法

卡爾曼濾波是一種遞推線性最小方差估計，其設計準則與線性最小方差估計相同，估值同樣是量測值的線性函數。由于卡爾曼濾波算法使用遞推算法，啟動時需要給定初始值在內的系統初值。給定的初值在滿足一定的條件下，濾波過程中估計可以始終無偏[9]。文獻[10]中的算法利用反饋控制來實現對狀態的估計，它根據前一時刻的系統狀態，估計出當前的系統狀態，然后根據當前時刻的實際觀測值作為反饋，來修正估計的狀態。因此，卡爾曼濾波算法可以分為兩個步驟：狀態預測和測量修正。狀態預測方程由前一刻系統狀態和噪聲方差預測出當前的系統狀態；而測量修正方程則負責修正，在狀態預測方程中得到的預測估計狀態中加入當前實際傳感器的信號，最終得到修正后的系統狀態。其濾波算法如圖2所示。

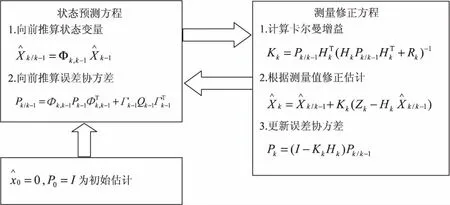
圖2 卡爾曼濾波算法

設tk時刻的被估計狀態Xk受系統噪聲序列Wk-1驅動，對Xk的兩側滿足線性關系，若離散線性系統描述為：

(2)

離散型卡爾曼濾波基本方程要滿足如下關系[11]：

狀態預測方程為：

(3)

測量修正方程為：

(4)

當狀態預測方程和測量修正方程循環運算時，就能使輸出信號越來越接近真值。使用卡爾曼濾波算法能夠有效過濾信號中的噪聲。

2.2 自平衡機器人算法模型

根據卡爾曼濾波原理[12]，設計濾波算法如下：

以機器人的重心距離豎直方向傾角anglek，陀螺儀的偏差量q_biask，作為狀態向量，得到相應的線性系統描述[13]。如公式(5)所示：

(5)

角度預測如下：

angle=angle-q_biask-1*dt+gyro_m*dt=angle+Rate*dt

(6)

方差預測如下：

(7)

角度偏量：

angle_err=incAngle-angle

(8)

濾波增益：

(9)

協方差更新：

(10)

狀態估計：

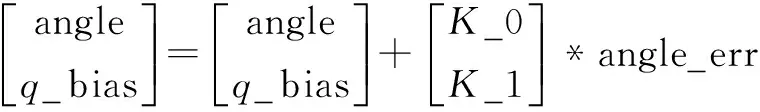
(11)

根據實際情況推導出工程應用算法實現模型，具體的實現方式在下一節介紹。

2.3 卡爾曼融合算法實現

定義函數為KalmanFilter，入口參數為陀螺儀角速度、加速度計。輸出參數為濾波角度。該函數主要實現卡爾曼數據融合的過程，計算最優估計角度。函數構造如下：

FloatKalmanFilter(constfloat gyro_m,const float incAngle)

{

定義參數并實現卡爾曼融合算法；

Return angle；

}

定義參數如下：

(1)濾波增益矩陣參數。

floatK_0;floatK_1;floatY_0;floatY_1

(2)去除偏差后的角速度。

floatRate

(3)計算狀態預測協方差矩陣的中間矩陣。

floatPdot[4]

(4)定義角度偏量和計算的中間量、下時刻最優估計值角度、陀螺儀的偏差。

floatangle_err;floatE;staticfloatangle=0;staticfloatq_bias=0

(5)定義狀態協方差。

staticfloatP[2][2]={{1,0},{0,1}}

(6)卡爾曼狀態更新。

angle+=Rate*dt

(7)計算預測協方差矩陣。

Pdot[0]=Q_angle-P[0][1]-P[1][0];

Pdot[1]=-P[1][1];Pdot[2]=-P[1][1];

Pdot[3]=Q_gyro;P[0][0]+=Pdot[0]*dt;

P[0][1]+=Pdot[1]*dt;P[1][0]+=Pdot[2]*dt;

P[1][1]+=Pdot[3]*dt

(8)計算角度偏量、卡爾曼增益。

angle_err=incAngle-angle

E=R_angle+P[0][0]

K_0=P[0][0]/E;K_1=P[1][0]/E;

Y_0=P[0][0];Y_1=P[0][1]

(9)更新協方差矩陣并給出最優估計值。

P[0][0]-=K_0*Y_0;P[0][1]-=K_0*Y_1;P[1][0]-=K_1*Y_0;P[1][1]-=K_1 *Y_1;

angle +=K_0*angle_err

(10)更新最優估計值偏差。

q_bias+=K_1*angle_err

通過上述步驟可以實現卡爾曼融合算法，將輸入的陀螺儀和加速度計的數據進行融合，得到角度信息并返回。

文中使用C語言對卡爾曼濾波器進行建模得到上述程序。其中，dt代表了離散系統中對傳感器陀螺儀和加速度計的采樣時間。Q_angle和Q_gyro分別代表速度計和陀螺儀測量的協方差，協方差取值的物理意義是對傳感器信號品質的一種評估。例如，如果認為加速度計測量的數據更可靠，就可以將Q_angle的值設置的較小，從而在濾波過程中體現這種可靠性。R_angle矩陣代表測量誤差的協方差。同理，R取值的大小就代表測量噪聲的大小。Q和R矩陣的取值，通過大量實驗獲取比較合理的參數值。

3 實驗平臺驗證

結合上述對卡爾曼濾波算法的分析，采用加速度計MMA7260和陀螺儀ENC03作為慣性傳感元件，對靜態和動態的機器人姿態進行平臺驗證，結果如圖3所示。

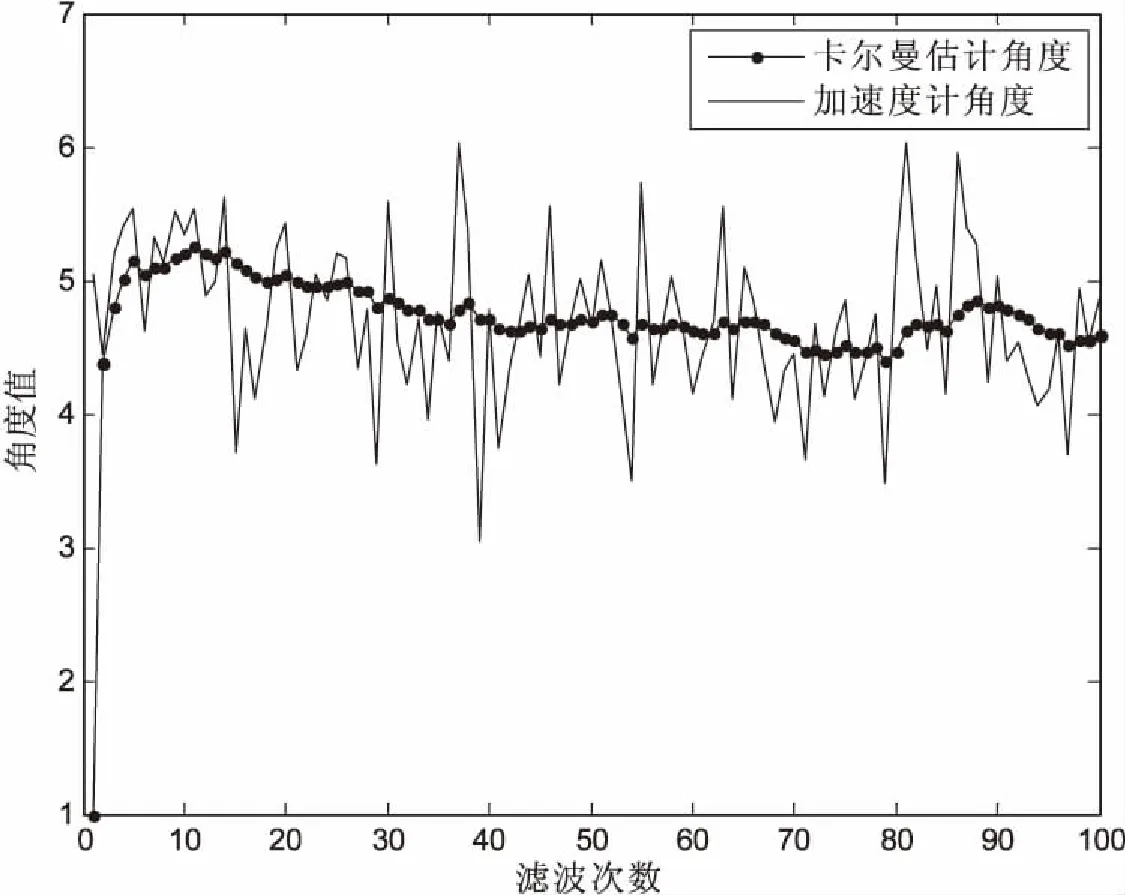
圖3 卡爾曼數據融合后的效果

4 結束語

輪式自平衡機器人是一種通用的機器人。它適用于各種復雜環境中，通過陀螺儀和加速度計采集的數據可以控制其平衡性，但是效果不夠好。為了進一步提高系統的性能，文中通過離散卡爾曼算法將ENC03陀螺儀和MMA7260加速度計采集的數據進行融合輸出。分別研究了傳統的卡爾曼算法，并詳細推導了如何建立適合自平衡機器人的算法模型，最后介紹并實現該算法。通過實時監測(見圖3)可以發現，在未進行角度融合之前，加速度計計算得出的角度在靜態和動態都有著極大的噪聲；經過卡爾曼濾波算法融合后的角度平滑穩定，達到了預期的效果。

[1] 王振宇.兩輪移動機器人平衡控制系統的研發[D].成都:西南交通大學,2010.

[2] 王小冬.卡爾曼濾波在衛星導航中的應用研究[D].大連:大連海事大學,2008.

[3] 秦永元,張紅鉞,汪叔華.卡爾曼濾波與組合導航原理[M].西安:西北工業大學出版社,2012:33-42.

[4] 席 峰,劉 中.基于信息矩陣加權一致策略的分布式Kalman濾波器[J].信息與控制,2010,39(2):194-199.

[5] 楊元喜.動態Kalman濾波模型誤差的影響[J].測繪科學,2006,31(1):17-18.

[6] 王學斌,徐建宏,張 章.卡爾曼濾波器參數分析與應用方法研究[J].計算機應用與軟件,2012,29(6):212-215.

[7] 陸如華,徐傳玉,張 玲,等.卡爾曼濾波的初值計算方法及其應用[J].應用氣象學報,1997,8(1):34-43.

[8] 邱 愷,黃國榮,陳天如,等.卡爾曼濾波過程中的穩定性研究[J].系統工程與電子技術,2005,27(1):33-35.

[9] 潘 泉,于 昕,程詠梅,等.信息融合理論的基本方法與進展[J].自動化學報,2003,29(4):599-615.

[10] 崔平遠,鄭黎方,裴福俊,等.基于卡爾曼/粒子組合濾波器的組合導航方法研究[J].系統仿真學報,2009,21(1):220-223.

[11] Kalman R E.A new approach to linear filtering and prediction problems[J].Transaction of the ASME-Journal of Basic Engineering,1960,82:35-45.

[12] Saber R O,Shamma J S.Consensus filters for sensor networks and distributed sensor fusion[C]//Proc of IEEE conference on decision and control.Seville:IEEE Press,2005:6698-6703.

[13] Ren W,Beard R W,Kingston D B.Multi-agent Kalman consensus with relative uncertainty[C]//Proc of American control conference.Oregon:IEEE Press,2005:1865-1870.

[14] Marco C,Giorgio F,Riccardo G,et al.Real-time data fusion and MEMS sensors fault detection in an aircraft emergency attitude unit based on Kalman filtering[J].IEEE Sensors Journal,2012,12(10):2984-2992.

Research and Implementation of Data Fusion Algorithm for Self-balancing Robot

LV Chuan-long1,CAO Hua-jie2,LIU Hao-dong1

(1.School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China;2.School of Information Science and Technology,Southwest Jiaotong University,Chengdu 611756,China)

Self-balancing robot is general and uses the data collected by gyroscope and accelerometer to control its balance,which can be applied to various complex environments.In order to improve the response of the system because of its limited accuracy and punctuality,the discrete Kalman algorithm is utilized for fusion of the data acquired from the gyroscope (ENC-03) and accelerometer (MMA-7260).Research of the traditional Kalman algorithm is carried on,then establishment of its model for self balancing robot,finally introduction of its engineering implementation.According to the real-time monitoring,it can be seen that the angle calculated from the accelerometer without angle infusion has great noise both in its dynamic and static aspects.The angle acquired from Kalman filtering algorithm fusion is smooth and stable,achieving the desired effect.

self balancing robot;accelerometer;gyroscope;Kalman algorithm;data fusion

2015-10-15

2016-01-21

時間：2016-06-22

全國大學生創新基金資助重點項目(201310292023Z)；江蘇省“挑戰杯-卓越杯”基金資助項目(201310292023Z)

呂傳龍(1992-)，男，碩士研究生，CCF會員，研究方向為機器人控制技術。

http://www.cnki.net/kcms/detail/61.1450.TP.20160622.0842.006.html

TP301.6

A

1673-629X(2016)08-0035-04

10.3969/j.issn.1673-629X.2016.08.007