基于矩陣自定義運算的Floyd改進算法

趙禮峰，黃奕雯

(南京郵電大學 理學院，江蘇 南京 210046)

基于矩陣自定義運算的Floyd改進算法

趙禮峰，黃奕雯

(南京郵電大學 理學院，江蘇 南京 210046)

解決最短路問題的算法層出不窮，其中最經典的要數Dijkstra算法和Floyd算法。但Dijkstra算法只能得出一對節點間的最短距離，而Floyd算法計算過程十分繁瑣。為解決這兩種經典算法中的缺陷，提出一種基于矩陣自定義運算的Floyd改進算法。該算法通過自定義矩陣運算得出一個表示兩兩節點間距離的路權修正矩陣，再用路權修正矩陣與原距離矩陣進行比較，選擇兩矩陣中對應較小元素組成當前最短路權矩陣，再通過有限次的迭代，從而得到各頂點間的最短路。通過MATLAB仿真，將該算法推廣到隨機大規模復雜網絡中，通過運行時間折線圖表明，該算法在節點達到一定數量后運行速度明顯優于傳統算法，且在稀疏網絡中運行效率非常高，說明了該算法的有效性。最后，通過具體應用說明了該算法的實用性。

最短路問題;Floyd算法;矩陣自定義運算;MATLAB;稀疏網絡

0 引 言

隨著社會的發展，最短路問題在日常生活中的應用越來越廣泛，小到上班上學走哪條路最近，大到網絡路由以及基站的選址，還有交通旅行、城市規劃、電網架設，最短路問題出現在生活的方方面面。如果掌握了最短路算法，那么可以給生活帶來許多便利。為了解決簡單的最短路問題，提出了許多簡便的算法，如Dijkstra算法、Floyd算法、Kruskal算法、拓撲排序法、啟發式搜索算法、A*算法、動態規劃算法以及神經網絡遺傳算法等等[1-6]。然而Dijkstra算法和Floyd算法無法解決任意頂點間最短路長的問題，而且Floyd算法十分繁瑣。

針對上述問題，文中提出了一種基于矩陣自定義運算的Floyd改進算法。該算法在計算權矩陣時直接在權值旁對路徑進行標注，省去了路徑矩陣的求解。同時，在運算過程中對矩陣元素出現∞時不進行運算，大大簡化了運算量。特別是在稀疏矩陣中，由于稀疏矩陣中有大量的∞元素，那么只需計算其中幾個非∞元素，算法優勢顯而易見。但是當階數n非常大時，計算依然十分復雜，所以需要借助計算機用計算機語言來實現大型網絡的計算。文中借助MATLAB實現該算法。

1 相關知識

定義1[7]賦權圖：設G=(V,E)為一幅圖，給G的每一條邊e賦予一個權值w(e),w(e)可以指網絡流量、運輸費用、物理距離、消耗時間等。若圖G的所有邊都賦予權值，稱G為賦權圖或網絡。

定義2[7]最短路徑：在帶權圖G=(V,E)中，若頂點vi，vj是圖G的兩個頂點，從頂點vi到vj的路徑長度定義為路徑上各條邊的權值之和。從頂點vi到vj可能有多條路徑，其中路徑長度最小的一條稱為頂點vi到vj的最短路徑。

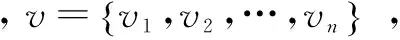
定義4[3]稀疏網絡：用稀疏矩陣存儲的網絡。

定義5、定義6是文中給出的：

定義5 稀疏矩陣：包含大量0元素的矩陣，在最短路問題中，可以認為含有大量∞元素的矩陣。

定義6 矩陣自定義運算⊕：現定義一種運算⊕，使得：

那么有：

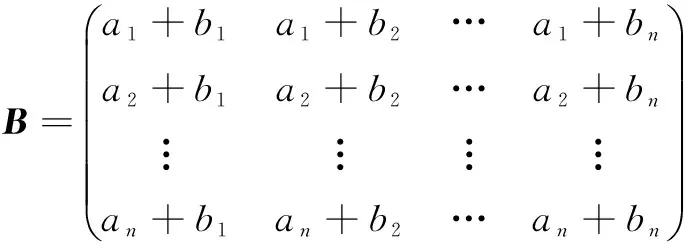
這種新定義的運算相當于連接兩條經過統一定點的路徑。每做一次⊕運算相當于原路徑經過一次中間節點。

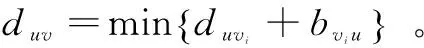
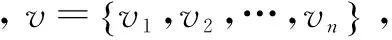
(1)

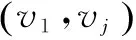
2 基于矩陣自定義運算的Floyd改進算法

2.1 算法思想

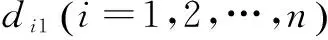
與此同時，以標注法直接在代表距離的權值旁的括號中標注路徑。當插入某個節點vk后，若計算出的最短路徑長度小于原來不經過vk時的長度，那么就將該節點的下標k直接標注在權矩陣中對應的元素的右邊括號中表明vk為最短路中路過節點，若路過節點不止一個則依次標明。

最后，當加法運算中一個加法項dij出現∞時，不用計算，直接得∞；當加法項dij出現0時，同樣無需計算，直接寫上另一個加法項，從而簡化計算。

2.2 算法步驟

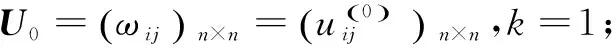
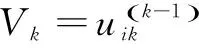
Step2:如果k=n，結束；否則，令k:=k+1,轉Step1。

2.3 算法復雜度分析

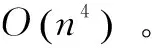
3 算 例

以圖1為例，得出各個頂點間的最短路。

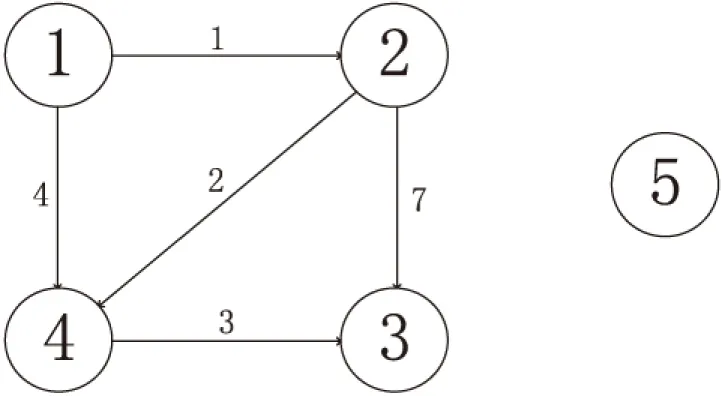
圖1 稀疏網絡

所以，經過V2和U0的比較，有

所以，經過V4和U2的比較，有

由于最后一行不用計算，所以U5=U4即為最終得出的結果。

4 算法的仿真與可行性分析

利用MATLAB[10]對文中提出的算法進行仿真。首先運行普通網絡，接著運行稀疏網絡，同時與傳統算法的運行作對比，通過運行時間的長短說明該算法的優越性。由仿真結果可知，該算法可以推廣到大規模隨機復雜網絡中，進一步說明了該算法的實用性。

由于是隨機生成的網絡，每次的運行結果有所差別，所以對它的運行時間取一個平均值。表1為對10階，20階，直到100階矩陣運行20次取得的平均結果，將它的運行時間與傳統Floyd算法進行比較。圖2為該改進算法與傳統算法運行時間相比的折線圖。

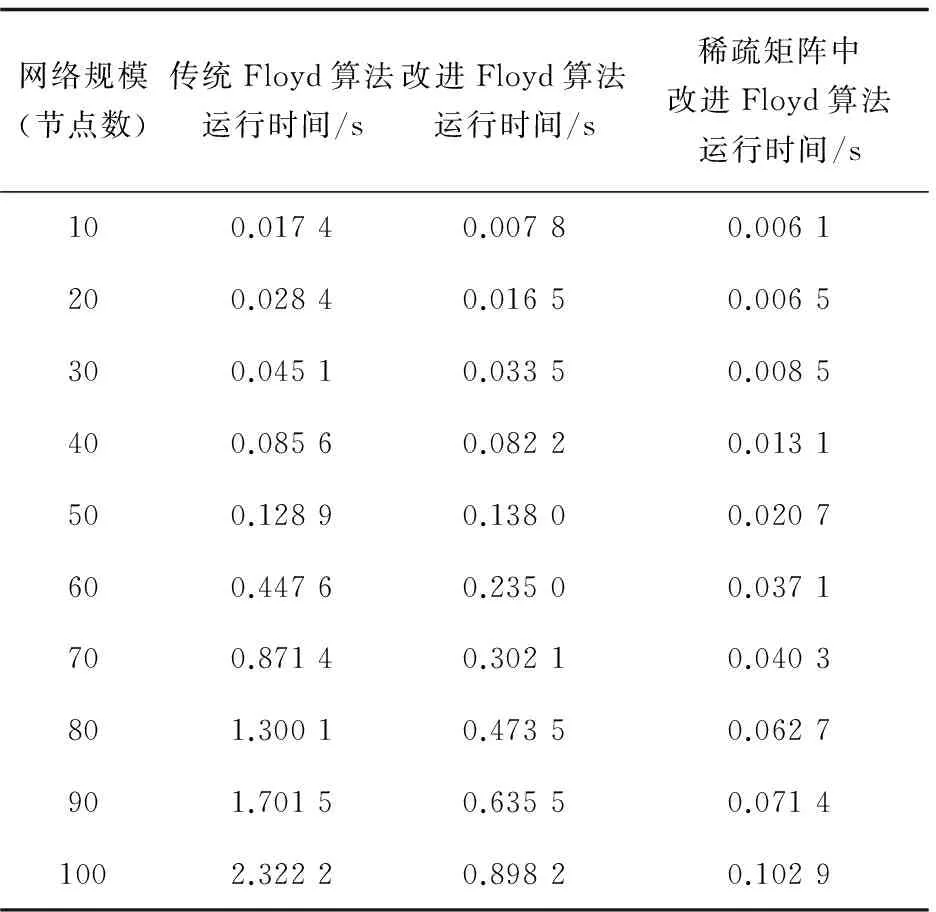
表1 算法運行時間

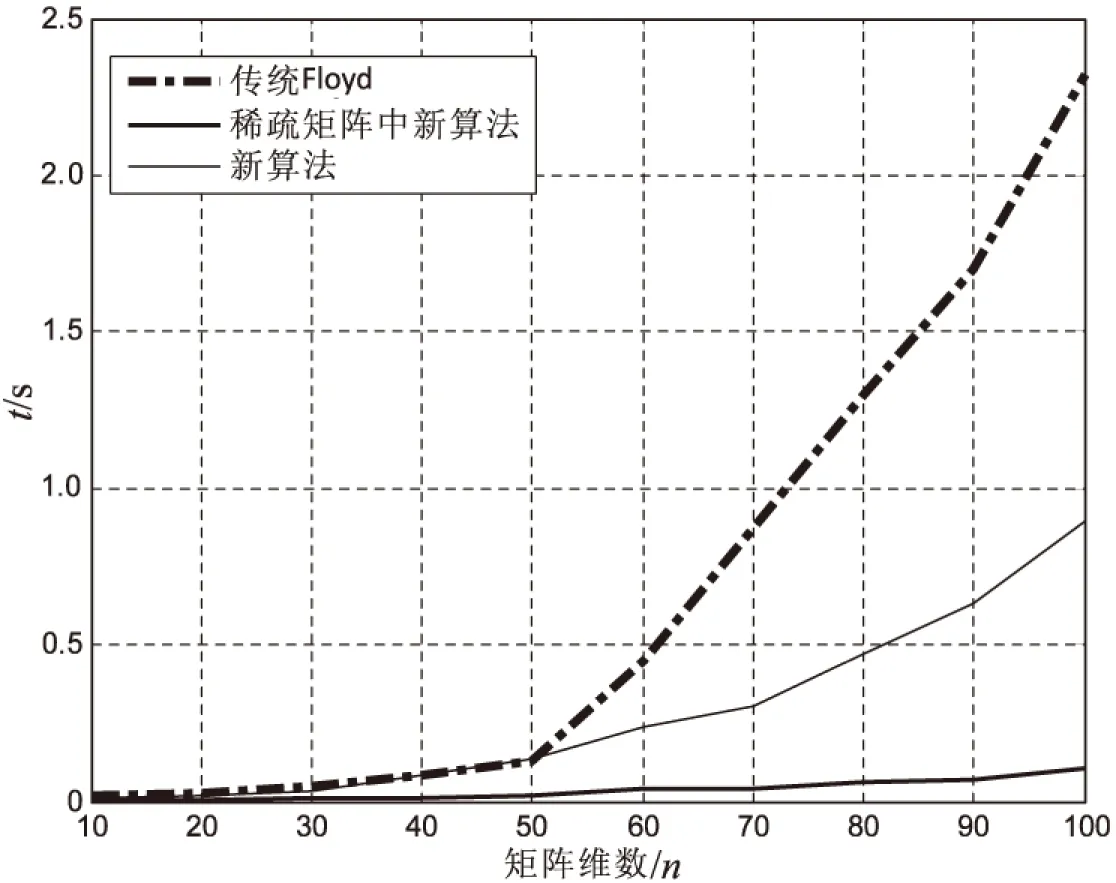
圖2 算法運行時間對比折線圖

5 實際應用舉例

最短路問題的應用非常廣泛,舉一個實際生活中存在的旅游班車選乘問題[11-14]的例子來說明最短路問題在生活中的應用。

例：南京旅游局開通了一條旅行專線,途中經過5個景點(奧體中心(A)、夫子廟(B)、中華門(C)、玄武湖(D)、中山陵(E))，每班車的發車時間固定(見表2)。如果在某一時刻出發從一個景點到另一個景點,討論不同時刻出發去某一景點的最短時間。(將路途中經過的時間看作是路的權值,那么，求最短時間的問題就可以看作是求最短路問題,即可以用文中求最短路的方法來解決。)

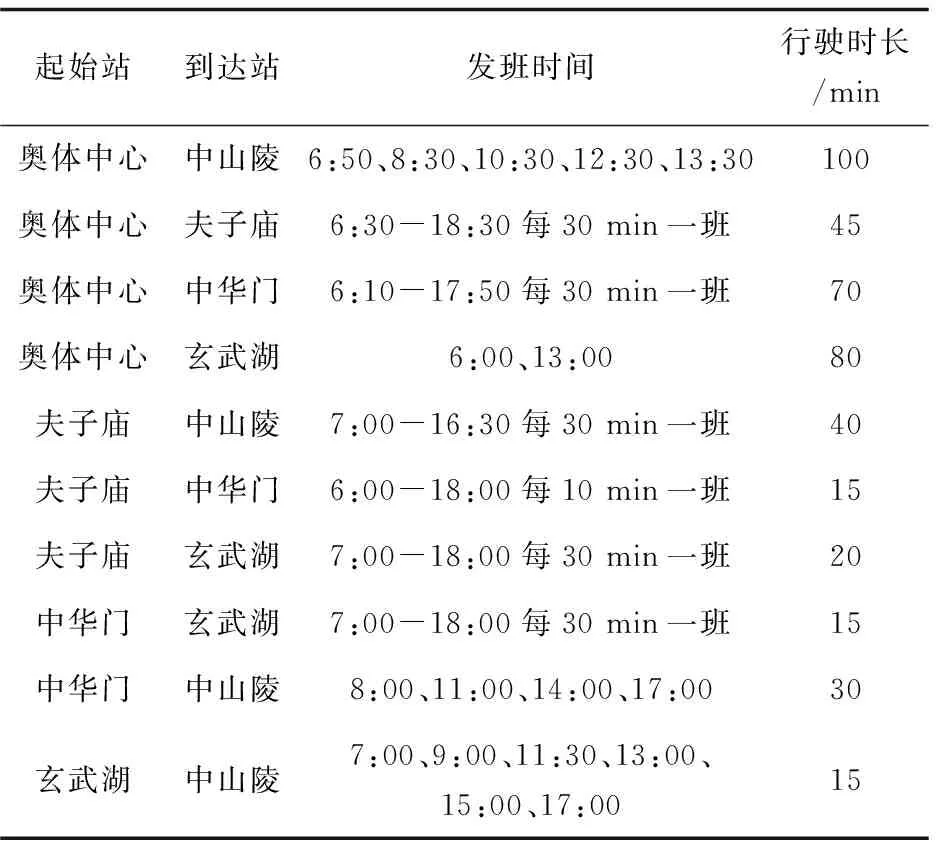
表2 班車時刻表

問：某人在11:30要從奧體中心出發去中山陵游玩，怎樣乘車才能最快到達？

解：把換乘旅行班車問題運用到圖論中轉化為最短路問題。首先，令奧體中心為A點(在本例中作為發點)，中山陵作為E點(在本例中作為收點)，做出旅行班車的路線圖，因為旅行班車停靠點時間固定，所以不同的出發時間，會有不同的時間圖，即圖中邊上的權值不同。圖3為11:30時出發的路線圖，為賦權無回路有向圖。

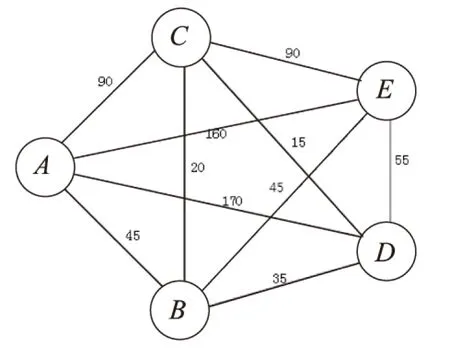
圖3 景點分布圖

初始矩陣為：

用以上算法求解最終得到：

由于最后一行不用計算，所以U5=U4即為最終得出的結果。

即，從奧體中心(A)到中山陵(E)最快需要90min，行駛路線為：奧體中心(A)→夫子廟(B)→中山陵(E)。

6 結束語

通過應用實例可以看出該算法在實際運用中的作用；經過程序測試，算法能夠得到任意節點間最短路。由仿真結果可以看出，當網絡節點較小時，該算法在一般網絡中與傳統算法相比，運行時間并沒有得到明顯提高；但是，當節點增多到50個以上時，該算法明顯快于傳統算法。同時，在稀疏網絡中，無論從時間復雜度，還是空間復雜度來說，文中算法優越性明顯。

[1] 張德全,吳果林,劉登峰.最短路問題的Floyd加速算法與優化[J].計算機工程與應用,2009,45(17):41-43.

[2] 張德全,吳果林.最短路問題的Floyd算法優化[J].許昌學院學報,2009,28(2):10-13.

[3] 吳果林,金 珍,鄧小方.稀疏網絡的Floyd動態優化算法[J].江西師范大學學報:自然科學版,2013,37(1):28-32.

[4] 鄧方安,雍龍泉,周 濤,等.基于“矩陣乘法”的網絡最短路徑算法[J].電子學報,2009,37(7):1594-1598.

[5] 趙禮峰,梁 娟.最短路問題的Floyd改進算法[J].計算機技術與發展,2014,24(8):31-34.

[6] 鄒桂芳,張培愛.網絡優化中最短路問題的改進Floyd算法[J].科學技術與工程,2011,11(28):6875-6878.

[7] 謝 政.網絡算法與復雜性理論[M].長沙:國防科技大學出版社,2003.

[8] 劉煥淋,陳 勇.通信網圖論及應用[M].北京:人民郵電出版社,2010.

[9] Hougardy S. The Floyd-warshall algorithm on graphs with negative cycles[J].Information Processing Letters，2010,110:279-281.

[10] 劉衛國.MATLAB程序設計與應用[M].北京:高等教育出版社,2006.

[11] 李 科,袁 明.小件快運中的最短運輸時間問題[J].山東交通科技,2011(5):23-25.

[12] Feillet D,Dejax P,Gendreau M.Traveling salesman problems with profits[J].Transportation Science,2005,39(2):188-205.

[13] Braess D,Nagurney A,Wakolbinger T.On a paradox of traffic planning[J].Transportation Science,2005,39(4):446-450.

[14] Zhan F B.Three fastest shortest path algorithms on real road networks[J].Journal of Geographic Information and Decision Analysis,1997,1(1):69-82.

Improved Floyd Algorithm Based on Customized Matrix Operations

ZHAO Li-feng,HUANG Yi-wen

(College of Mathematics and Physics,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

The algorithm to solve the shortest path problem is endless,and the algorithm of Dijkstra and Floyd is the most typical.However,the Dijkstra algorithm can only get the shortest distance between a pair of nodes,and Floyd algorithm is very cumbersome.For solving their defects in two classical algorithms,an improved Floyd algorithm is proposed based on matrix custom operation.It obtains a modified matrix between two nodes by using a customized matrix calculation,and then compares the modified matrix with the original distance matrix,selecting the smaller matrix elements for composition of the shortest path weight matrix.Through finite iteration,the shortest path is obtained between each vertex.By the MATLAB simulation,the algorithm is extended to stochastic large-scale complex networks.The running time line chart shows that this algorithm runs faster than traditional algorithm after a certain number of nodes,and in sparse network,the efficiency is particularly high,which shows the its effectiveness.Finally,by using the specific application,the feasibility of the algorithm is verified.

shortest path problem;Floyd algorithm;matrix custom operations;MATLAB;sparse network

2015-11-23

2016-03-03

時間：2016-08-01

國家自然科學基金資助項目(61304169)

趙禮峰(1959-),男,教授,碩士研究生導師,研究方向為圖論及其在通信中的應用;黃奕雯(1991-),女,碩士研究生,研究方向為圖論及其在通信中的應用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0904.024.html

TP301.6

A

1673-629X(2016)10-0041-04

10.3969/j.issn.1673-629X.2016.10.009