基于機器學習的學生成績預警系統建模與研究
吳鯤
(江蘇聯合職業技術學院揚州商務分院,江蘇 揚州 225127)
基于機器學習的學生成績預警系統建模與研究
吳鯤
(江蘇聯合職業技術學院揚州商務分院,江蘇 揚州 225127)
隨著高校智慧校園建設的深入,所采集的校園大數據呈幾何基數增長,如何充分利用大數據對校園學習生活進行科學的預測與示警是智慧校園建設研究的重大課題。為了彌補以往的技術不足,采用機器學習技術應用于成績預警這個領域中,隨機森林算法、應用支持向量機(SVM,Support Vector Machine)、線性回歸、回歸分類樹等技術,詳細論述了高校學生成績預警系統的基于機器學習的成績預警功能的設計與實現。
機器學習;隨機森林算法;SVM;成績預警;智慧校園
高校的智慧校園建設正如火如荼地進行,作為數字化校園的更高級階段,智慧校園建設強調的是“智慧”,突出的是智能,如何利用大數據技術、云服務、物聯網等技術,以人為本地為師生、家長、社會提供信息化服務,以達到為學生的發展和終生幸福打好扎實的基礎,是智慧校園建設研究的熱點問題。高校學生成績管理是高校教務系統管理的核心,以往的學生成績管理系統只關注于學生學習數據的分析,計算不同成績產生的概率,通過一定的算法推定未來的成績從而產生預警。這種方法將學生的學習獨立于學生的校園活動之外,有其局限性。通過智慧校園產生的大數據,充分采集學生的大數據,如進入圖書館學習的時間、通過門禁進入實訓室的時間、校園消費軌跡、網絡上網日志等數據,采用隨機森林算法建立起高校學生成績預警系統,以期對學習行為進行警示,全面提高學生的成績。
一、相關技術綜述
(一)決策樹
數據的分類以樹形結構的方式呈現,每個分支都代表著不同的分類情況。分類的標準分為信息增益法,用信息的增益作為分類劃分的標準,如ID3、C4.5算法、基尼指數法。用數據劃分的純度來做比較,最典型的就是CART分類回歸樹所用的方法,樹構造好了之后,可以有剪枝的操作。
(二)隨機森林
隨機森林算法是用隨機的方式來建立一個森林,森林有決策樹,每個決策樹生成是隨機的,它們之間是沒有關聯的。當有一個新的輸入樣本進入的時候,就讓森林中的每一棵決策樹分別進行一下判斷,看看這個樣本應該屬于哪一類(對于分類算法),然后看看哪一類被選擇最多,就預測這個樣本為那一類。
在傳統的CART算法中,每個內部節點都是原始數據集的子集,根節點包含了所有的原始數據而在每個內部節點處,從所有屬性中找出最好的分裂方式進行分裂,然后對后續節點依次進行分裂,直到葉子節點最后通過剪枝使測試誤差最小。與其他算法不同,隨機森林中單棵樹的生長可概括為以下幾點:
1.使用Bagging方法形成各異的訓練集;假設原始訓練集中的樣本數為N,從中有放回地隨機選取個樣本形成一個新的訓練集,以此生成一棵分類樹。
2.隨機選擇特征對分類回歸樹的內部節點進行分裂;假設共有M個特征,指定一個正整數m〈〈M,在每個內部節點,從M個特征中隨機抽取m個特征作為候選特征,選擇這個m特征上最好的分裂方式對節點進行分裂。在整個森林的生長過程中,M的值保持不變。
3.每棵樹任其生長,不進行剪枝。
(三)支持向量機(SVM)
支持向量機(SVM)是在統計學習理論和結構風險最小原理基礎上發展起來的一種新的機器學習方法,是解決非線性分類、函數估算、密度估算等問題的有效手段,主要思想是建立一個最優決策超平面,使得該平面兩側距平面最近的兩類樣本之間的距離最大化,從而對分類問題提供良好的泛化能力。根據有限的樣本信息在模型中特定訓練樣本的學習精度和無錯誤地識別任意樣本的能力之間尋求最佳最精確的結果,保證了模型具有全局最優、最大泛化能力、推廣能力強等優點,在解決小樣本、非線性及高維模式識別中表現出許多特有的優勢,并能夠推廣應用到函數擬合中,能夠很好地解決許多實際預測問題。
二、預測模型的建立
(一)關鍵數據的提取
為了對學生的期末成績走向有一個合理的預測,根據校園生活實際經驗進行了關鍵詞的選取,本文從3個大項、12個小項進行了關鍵數據的提取,涵蓋了學生進入圖書館學習的時間、學生吃飯的時間、學生的課堂學習時間、通過門禁進入實訓室的時間、進入機房的時間、校園消費記錄、進入宿舍時間、學生上網學習的時間、學生上網游戲的時間、學生上網休閑的時間作為關鍵數據進行深入的挖掘,所采集的數據是江蘇聯合職業技術學院揚州商務分院所有學生采集的大數據。
(二)數據特征值的提取

表1 關鍵數據表
特征的選取對于構建決策樹的分類十分重要,提取出合適的特征值對于預測學生成績發展的趨勢具有十分重要的意義。在選擇特征值時,希望發現那些對學生成績波動影響特別大的特征集。
決策樹(隨機森林)的特征值的選取依賴于已知數據,利用決策樹我們對測試集進行分類,以此判斷是否需要對學生進行預警。在這個過程中,由于樹的劃分太細,很容易造成過擬合的問題。在這里,我們可以利用剪枝來確認最終的特征值,剪枝的方法主要有如下幾種:(1)錯誤率降低剪枝:最簡單的剪枝方法,減少某個節點看是否能夠提高正確率(利用訓練集來驗證正確率而不是測試集)。(2)悲觀剪枝:主要依據概率論根據自身節點比較信息增益來進行剪枝。(3)代價復雜度:主要是通過增加新的節點看是否能大幅提升準確率,通過閾值來判斷是否增加新的節點)。隨機森林的本質就是多棵決策樹的組合,利用不怎么準確的決策方法生成最終一個可靠的結果。
三、基于隨機森林的學習成績預測算法
(一)模型的算法
首先我們得到決策樹,下面我們就需要進行相對應的剪枝。這里我們利用剪枝前后信息熵的變化來說明。以屬性R分裂前后的信息增益比其他屬性最大。這里信息的定義如下:

其中的m表示數據集D中類別C的個數,Pi表示D中任意一個記錄屬于Ci的概率,計算時Pi=(D中屬于Ci類的集合的記錄個數/|D|)。Info(D)表示將數據集D不同的類分開需要的信息量。
熵表示的是不確定度的度量,如果某個數據集的類別的不確定程度越高,則其熵就越大。比如我們將學生上網瀏覽的目的定義為f1,f1的取值為{1,2,3,4,5,6},代表有六種不同的可能性,則f1的熵entropy(f1)=-(1/6*log (1/6)+…+1/6*log(1/6))=-1*log(1/6)=2.58;我們將學生進入圖書館的目的定義為f2,f2的取值為 {1,2,3,4},f2的熵entropy(1)=-(1/4*log(1/4)+1/4*log(1/4)+1/4*log(1/4) +1/4*log(1/4)) =-log(1/4)=2;將學生進入實訓室的目的定義為f3,顯然學生進入實訓室一定是為了學習,即f3的取值為{1},故其熵entropy(f3)=-1*log(1)=0。可以看到,可能的情況越多,熵值也越大。而當只有一個可能時,熵值為0,此時表示不確定程度為0,也就是學生的目的是確定的。
有了上面關于熵的運算,我們接著計算信息增益。假設我們選擇屬性R作為分裂屬性,數據集D中,R有k個不同的取值{V1,V2,…,Vk},于是可將D根據R的值分成k組{D1,D2,…,Dk},按R進行分裂后,將數據集D不同的類分開還需要的信息量為:
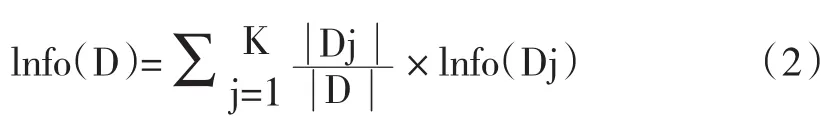
信息增益的定義為分裂前后,兩個信息量只差:
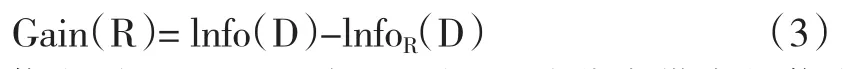
信息增益Gain(R)表示屬性R給分類帶來的信息量,我們尋找Gain最大的屬性,就能使分類盡可能的純,即最可能地把不同的類分開。不過我們發現,對所有的屬性Info(D)都是一樣的,所以求最大的Gain可以轉化為求最新的。
(二)實際預測過程
下面這個例子會預測學生是否沉迷于網絡,首先我們得到如此的決策樹,下面就需要進行相對應的剪枝。因為不同年級的課余時間不一樣,我們將年級作為一個特征值,學生到課率作為第二個特征值,學生上網日志訪問游戲類網站地址的頻率作為第三個特征值;將學生上網頻率作為第四個特征值。數據集D如附表1:
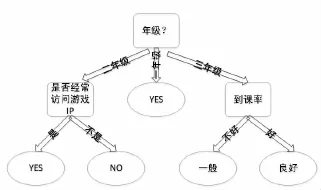
圖1 決策樹
附表1的數據集是根據學生的年級、上網頻率、是否經常訪問游戲IP以及到課率來確定他是否會沉迷于網絡,即最后一列“是否沉迷于網絡”是類標。現在我們用信息增益選出最佳的分類屬性,計算按年級分裂后的信息量:
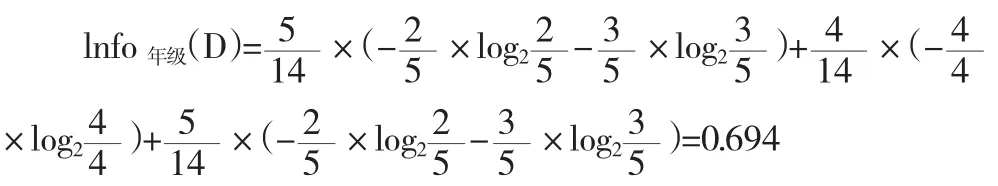
整個式子由三項累加而成,第一項為一年級,14條記錄中有5條為一年級,其中2(占2/5)條沉迷于網絡,3(占3/5)條不沉迷于網絡。第二項為二年級,第三項為三年級。類似的有:
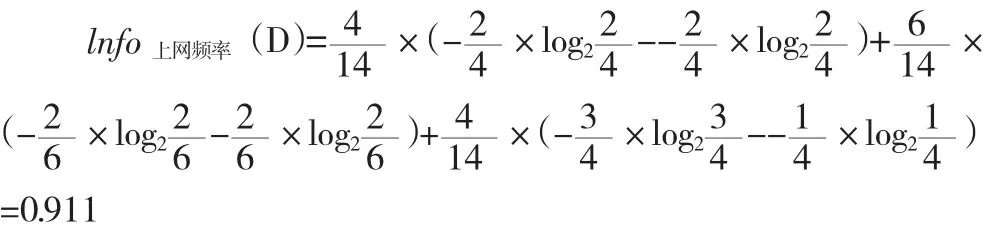
同理,得出:lnfo訪問游戲(D)=0.789 ,lnfo到課率(D)=0.892
可以得出lnfo年級(D)最小,說明不要增加信用等級這個節點,增加之后不確定新增加,即以年級分裂后,分得的結果中類標最純,此時以年級作為根結點的測試屬性。
由于數據來源不同,存在不同的結果結合。這里首先根據隨機森林得到相對應的分類。然后進行剪枝,得到相對應的特征,再利用這些特征對結果進行分類,同時我們把這個隨機森林方法應用到歷史的情況,利用提取學生的一卡通、門禁等各種數據以及SVM方法來擬合某學期成績的升降(采用交叉檢驗,使得結果具有穩定性不至于出現過擬合的問題)。利用這個擬合函數來預測學生本學期的分差,而如果結果的趨勢和Tree的判別趨勢相同我們就選擇采信這種方法,如果兩個結果趨勢矛盾,我們將利用這個學生本人的歷史數據再次進行SVM模擬,將結果加入到之前的SVM模型當中。
用SVM方法來擬合歷史上特征量的變化和最終分差的差別,利用這個SVM擬合來擬合本學習期學生的變化得到最終的分差。這里的分差表示學生本學期均分和以往均分的變化,正值表示學生成績下滑,負值表示學生成績上升。因此,我們就可以在學期中通過這種算法不斷提醒某些學生可能存在成績下滑的危險或大幅度上升的趨勢。
四、預測結果與分析
(一)預測結果
完成對模型建模與計算后,分別對學校一年級、二年級、三年級的學生數據進行分類與擬合,計算最終分差,這里截取了部分同學的分差,如表2,并形成年級成績分差趨勢圖,如圖2。
(二)結果分析
如圖3所示,我們將2015年學校三個年級成績趨勢分差的預測值和學校三個年級實際成績分差進行了對比,模型擬合效果總體成績趨勢較為理想,但預測分差值和實際分差值浮動的幅度還是較大,需要在以后的研究中再引入其他數據加以改進。
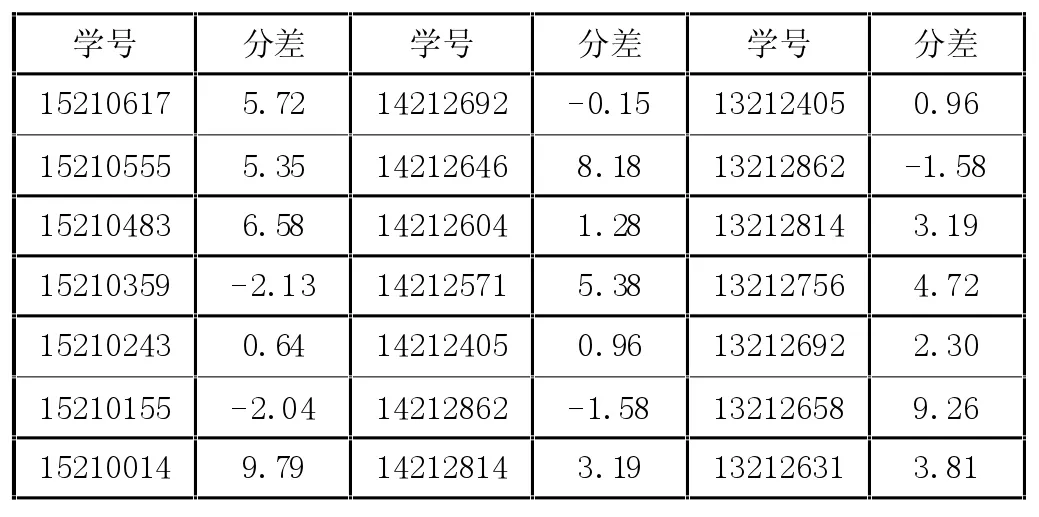
表2 各年級學生成績分差
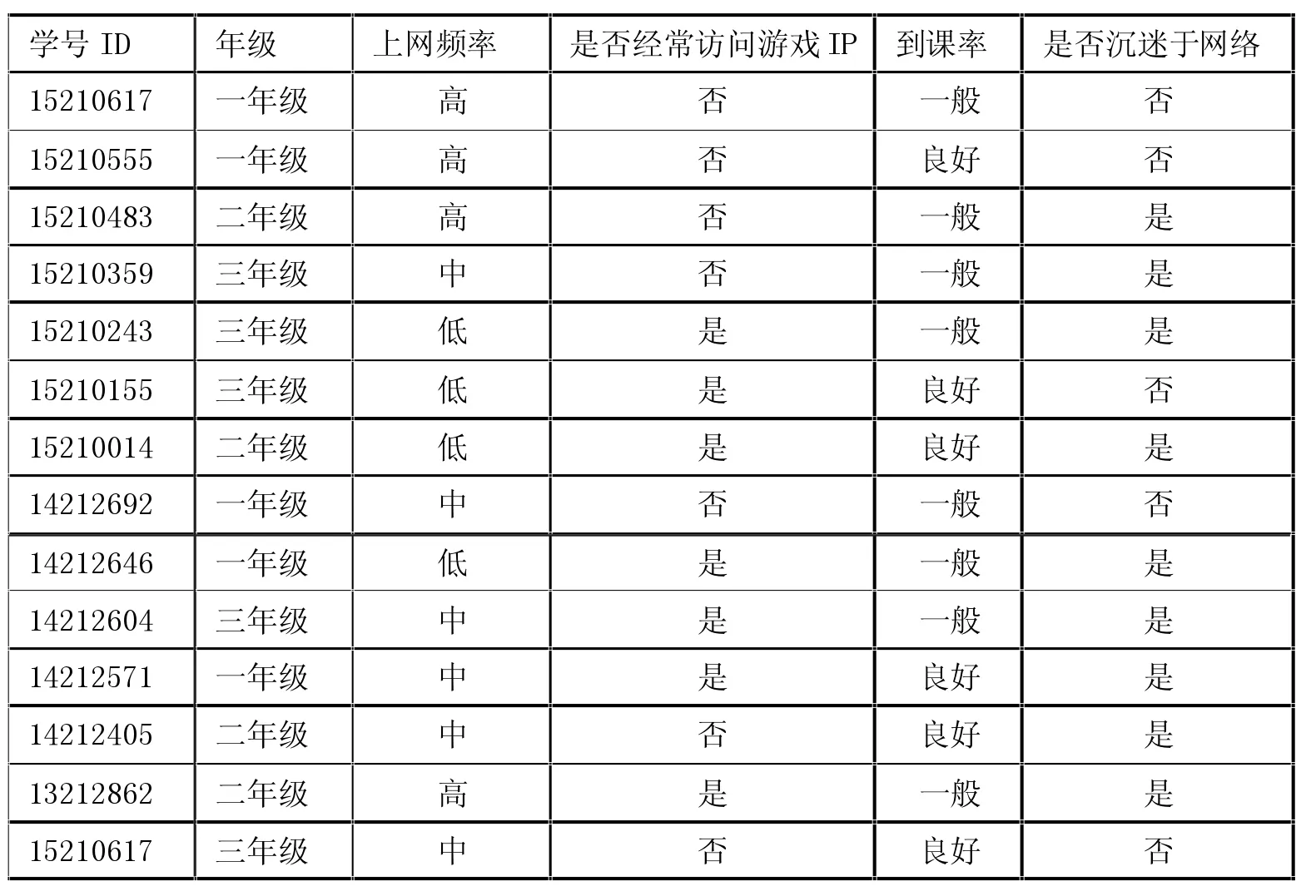
附表1 學生上網數據統計
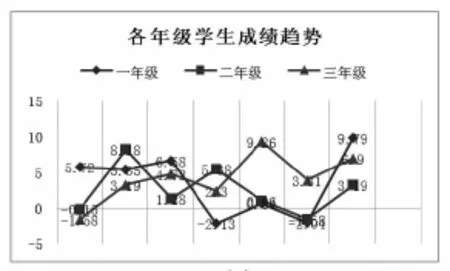
圖2 各年級學生成績分差趨勢
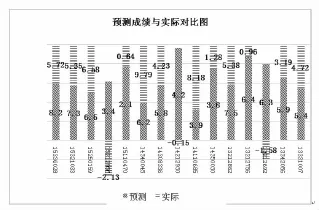
圖3 預測成績與實際對比圖
[1]Brett Lanta.機器學習與R語言[M].北京:機械工業出版社,2015:5-17.
[2]方匡南,吳見彬,朱建平,謝邦昌.隨機森林方法研究綜述[J].統計與信息壇,2011(3):32-38.
[3]董師師,黃哲學.隨機森林理論淺析[J].集成技術,2013(1):1-7.
[4]劉華煜.基于支持向量機的機器學習研究[D].大慶石油學院,2005.
[5]王全才.隨機森林特征選擇[D].大連理工大學,2011.
TP
A
1673-0046(2016)12-0178-03

