接觸網(wǎng)參數(shù)對接觸網(wǎng)風(fēng)致響應(yīng)的影響及風(fēng)洞試驗驗證
劉改紅
(中鐵第一勘察設(shè)計院集團有限公司,西安 710043)
?
接觸網(wǎng)參數(shù)對接觸網(wǎng)風(fēng)致響應(yīng)的影響及風(fēng)洞試驗驗證
劉改紅
(中鐵第一勘察設(shè)計院集團有限公司,西安710043)
摘要:大風(fēng)作用會使接觸網(wǎng)發(fā)生更大更復(fù)雜的振動與風(fēng)偏,為給大風(fēng)區(qū)接觸網(wǎng)的防風(fēng)設(shè)計提供科學(xué)依據(jù),采用有限元計算與風(fēng)洞試驗相結(jié)合的方法進行研究。利用ANSYS軟件建立包括支撐結(jié)構(gòu)和懸掛部分的有限元耦合模型;采用諧波合成法(WAWS)模擬針對接觸網(wǎng)結(jié)構(gòu)特點的脈動風(fēng)場;通過計算不同接觸網(wǎng)參數(shù)組合方案在風(fēng)荷載下的風(fēng)致響應(yīng)位移,定量分析得出懸掛類型、張力組合、跨距對接觸網(wǎng)風(fēng)致響應(yīng)的影響。接觸網(wǎng)氣動彈性風(fēng)洞試驗結(jié)果表明,接觸網(wǎng)參數(shù)對風(fēng)致響應(yīng)的影響的研究結(jié)果正確。研究成果應(yīng)用于蘭新鐵路第二雙線大風(fēng)區(qū)接觸網(wǎng)系統(tǒng)方案設(shè)計和技術(shù)參數(shù)選擇,并作為主要理論支撐之一,形成了首個國內(nèi)外鐵路電化行業(yè)的風(fēng)區(qū)接觸網(wǎng)裝備技術(shù)條件。
關(guān)鍵詞:接觸網(wǎng)參數(shù);風(fēng)致響應(yīng);風(fēng)洞試驗;定量分析;高速鐵路
地處新疆的蘭新鐵路第二雙線、蘭新鐵路既有線和南疆鐵路沿線經(jīng)過的風(fēng)區(qū)很多,其中百里風(fēng)區(qū)、三十里風(fēng)區(qū)的風(fēng)力最為強勁、最大風(fēng)速達64 m/s(超過17級),大風(fēng)頻繁,8級以上大風(fēng)天數(shù)年平均超過100 d,是我國乃至世界上鐵路風(fēng)災(zāi)最嚴(yán)重的地區(qū)之一。歷年來因大風(fēng)列車停運時有發(fā)生,并發(fā)生翻車等重大安全事故,嚴(yán)重威脅鐵路的行車安全。接觸網(wǎng)作為懸索結(jié)構(gòu)、沿鐵路線露天布置,大風(fēng)等外部環(huán)境因素嚴(yán)重影響其安全可靠性;另外,接觸網(wǎng)線長點多,且無備用,一旦出現(xiàn)故障將導(dǎo)致列車停駛,其防風(fēng)安全問題已經(jīng)成為大風(fēng)區(qū)高速鐵路建設(shè)和電氣化改造的難點[1]。
目前,國內(nèi)外對于平均風(fēng)與脈動風(fēng)作用下的接觸網(wǎng)風(fēng)致響應(yīng)進行了理論計算方面的研究[1-5],但尚未定量、系統(tǒng)地分析接觸網(wǎng)懸掛類型、張力組合等參數(shù)對接觸網(wǎng)風(fēng)致響應(yīng)的影響;已見諸報導(dǎo)的接觸網(wǎng)專業(yè)領(lǐng)域內(nèi)的風(fēng)洞試驗主要涉及受電弓的氣動力控制和擋風(fēng)墻高度對接觸線處橫風(fēng)的影響方面[6-7]。
以蘭新鐵路第二雙線為項目背景,建立接觸網(wǎng)有限元模型,利用諧波合成法模擬脈動風(fēng)速時程,在有限元模型中施加風(fēng)荷載作用,定量計算不同接觸網(wǎng)參數(shù)組合方案的風(fēng)振響應(yīng),系統(tǒng)分析了接觸網(wǎng)懸掛類型、跨距和張力組合對接觸網(wǎng)風(fēng)致響應(yīng)的影響。并開展了接觸網(wǎng)氣動彈性風(fēng)洞試驗,與理論計算結(jié)果進行對比、驗證。
1接觸網(wǎng)有限元模型的建立
由于懸索結(jié)構(gòu)的幾何非線性,在接觸網(wǎng)不同的初始狀態(tài)施加相同荷載增量引起的效應(yīng)不同,故需要通過靜態(tài)找形確定其初始狀態(tài)[2]。首先,確定系統(tǒng)初始構(gòu)型,采用BEAM44單元模擬支柱、腕臂、腕臂支撐、定位管、定位器及定位器支座;由于承力索、接觸線、吊弦受拉力作用,采用軸向僅受拉的桿單元link10模擬;因為腕臂支撐裝置是整體式旋轉(zhuǎn)腕臂,所以釋放上下腕臂底座與支座連接點的z方向旋轉(zhuǎn)自由度;定位器與定位支座可視為鉸接,釋放連接點的x、y、z三個方向的旋轉(zhuǎn)自由度;將各個支柱的底部節(jié)點、承力索和接觸線兩側(cè)終端的節(jié)點全約束。其次,使支柱和腕臂結(jié)構(gòu)剛性化,進行承力索在承力索、接觸線、吊弦和定位器重力作用下的幾何非線性分析,積累重力剛度;然后,恢復(fù)支柱和腕臂結(jié)構(gòu)的彈性,進行懸掛系統(tǒng)與支撐系統(tǒng)的耦合分析,最終完成懸掛系統(tǒng)的找形工作。如果模型中承力索的張力、弛度與理論計算結(jié)果一致,則靜態(tài)找形正確。以表1所示的簡鏈接觸網(wǎng)系統(tǒng)為例,建立的接觸網(wǎng)有限元模型如圖1所示。
2風(fēng)荷載的計算與模擬
風(fēng)一般可以分為平均風(fēng)和脈動風(fēng)兩部分,假設(shè)作用于結(jié)構(gòu)上坐標(biāo)為(x,y,z)的點的風(fēng)速為
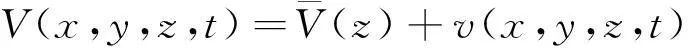
(1)
式中,右邊相加的兩部分分別為距地面高度z處的平均風(fēng)速和對應(yīng)的脈動風(fēng)速。風(fēng)的模擬主要針對脈動風(fēng)而言[7-9]。
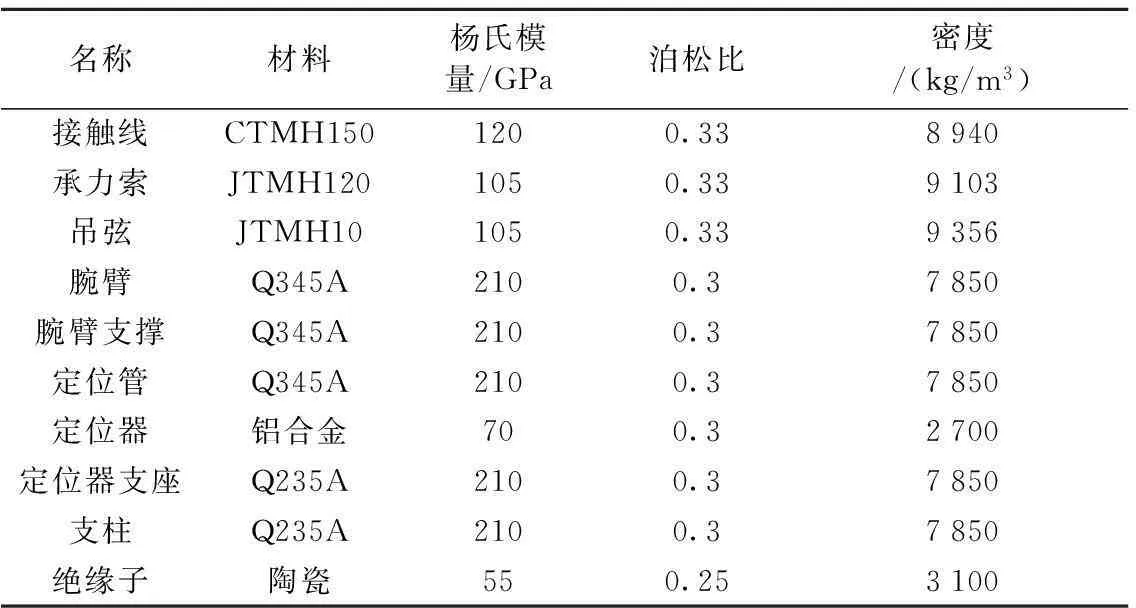
表1 接觸網(wǎng)系統(tǒng)基本參數(shù)
注:接觸網(wǎng)結(jié)構(gòu)高度1.1 m、跨距50 m、接觸線張力28.5 kN、承力索張力21 kN。
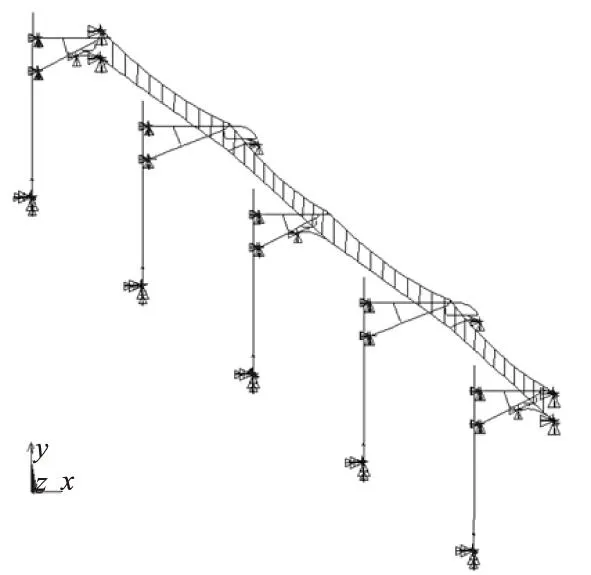
圖1 接觸網(wǎng)有限元模型
2.1 平均風(fēng)的計算
在空間上,平均風(fēng)速會隨著高度的變化而變化,本文選取指數(shù)率[10,11]計算,具體公式
(2)
式中,v10為距離地面10 m高度處的環(huán)境風(fēng)速,標(biāo)準(zhǔn)參考高度取10 m;H為當(dāng)前高度;α為地表粗糙度指數(shù),這里按0.16;K為擋風(fēng)屏后接觸線、承力索高度處的風(fēng)速系數(shù),這里按橋梁4 m擋風(fēng)屏風(fēng)場風(fēng)洞試驗結(jié)果取值,即接觸線處風(fēng)速系數(shù)0.76,承力索處風(fēng)速系數(shù)1.21。
2.2 脈動風(fēng)的模擬
為計算接觸網(wǎng)水平方向的風(fēng)偏和豎直方向的振動位移,分別選用經(jīng)Simiu修正的Kaimal譜(式3)和Lumley-Panosfsky譜(式4)模擬水平脈動風(fēng)速時程和豎向脈動風(fēng)速時程[13,14]。
(3)
(4)
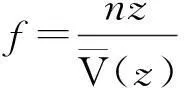
空間任意兩點脈動風(fēng)速互譜的相干函數(shù)[15]如下
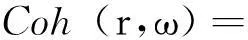
(5)
計算水平向脈動風(fēng)速互譜的相干函數(shù)時Cz和Cy分別取為10和16;計算豎向脈動風(fēng)速互譜的相干函數(shù)時Cz和Cy分別取為7和8。
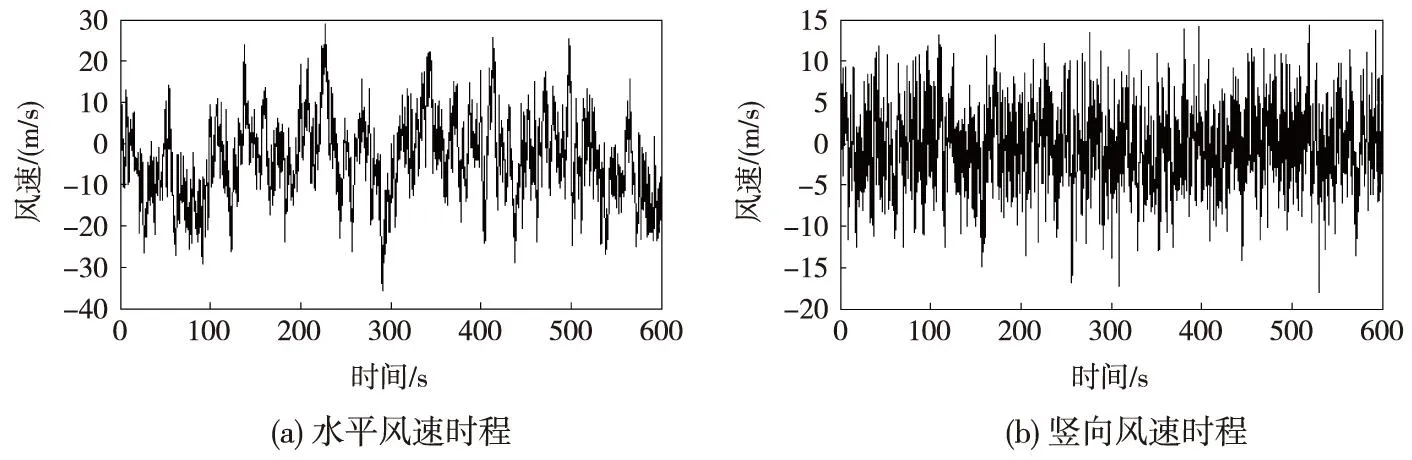
圖2 簡鏈其中一跨定位點處的風(fēng)速時程
按上述方法及風(fēng)譜,模擬出水平風(fēng)速時程和豎向風(fēng)速時程,選取簡鏈其中一跨定位點處為例,模擬的風(fēng)速時程見圖2。其中模擬計算的主要參數(shù)為截止頻率4π rad/s、頻率分段數(shù)1 024、樣本時間間隔0.25 s。
對模擬得到的風(fēng)速時程進行統(tǒng)計分析,得到其均值和均方根,與目標(biāo)譜對應(yīng)的值進行對比,如表2所示。從表2可以看出,模擬風(fēng)速的均值、均方根與目標(biāo)風(fēng)速相差均較小。
圖3所示為風(fēng)速時程的功率譜與目標(biāo)譜的比較,模擬的水平功率譜及低頻段豎向功率譜與目標(biāo)譜無論極值還是趨勢都吻合很好,豎向功率譜在高頻段雖然極值有一定差別,但整體趨勢較為吻合。

表2 風(fēng)速統(tǒng)計數(shù)據(jù)對比
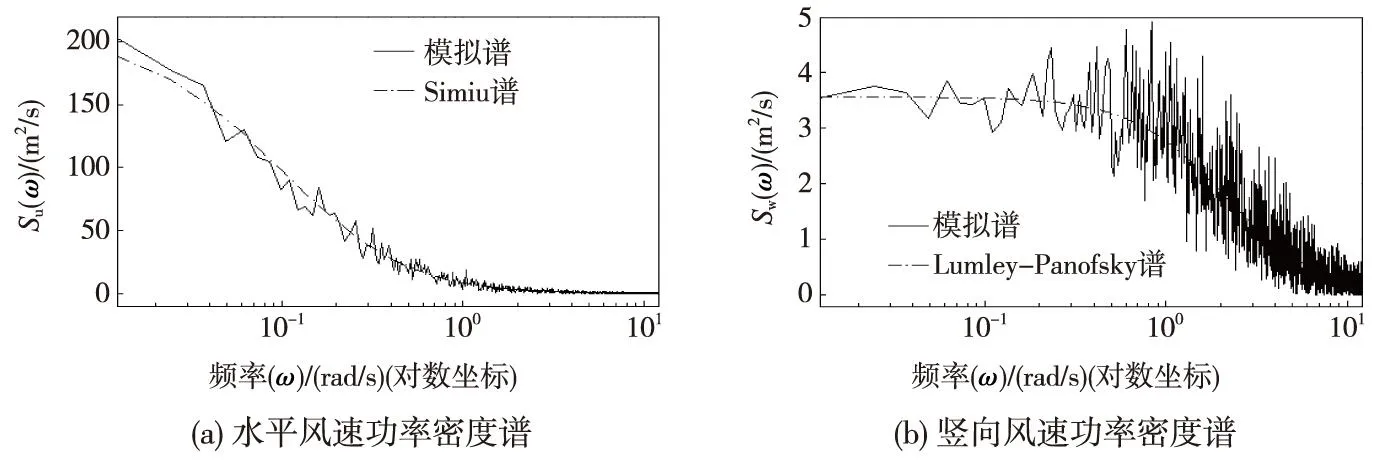
圖3 模擬的風(fēng)速功率譜與目標(biāo)譜的比較
3接觸網(wǎng)風(fēng)致響應(yīng)計算及影響分析
對不同接觸網(wǎng)參數(shù)組合方案(表3)進行正定位、反定位、跨中風(fēng)致振動及跨中風(fēng)偏的動態(tài)計算,根據(jù)計算結(jié)果,分析研究接觸網(wǎng)懸掛類型、張力及跨距對風(fēng)致響應(yīng)的影響。
3.1 接觸網(wǎng)風(fēng)致響應(yīng)計算
在接觸網(wǎng)有限元模型中施加風(fēng)壓作用,利用空氣動力學(xué)理論[16]計算接觸網(wǎng)平均位移,采用時程分析方法[17,18]計算接觸網(wǎng)抖振位移;疊加豎向平均位移與豎
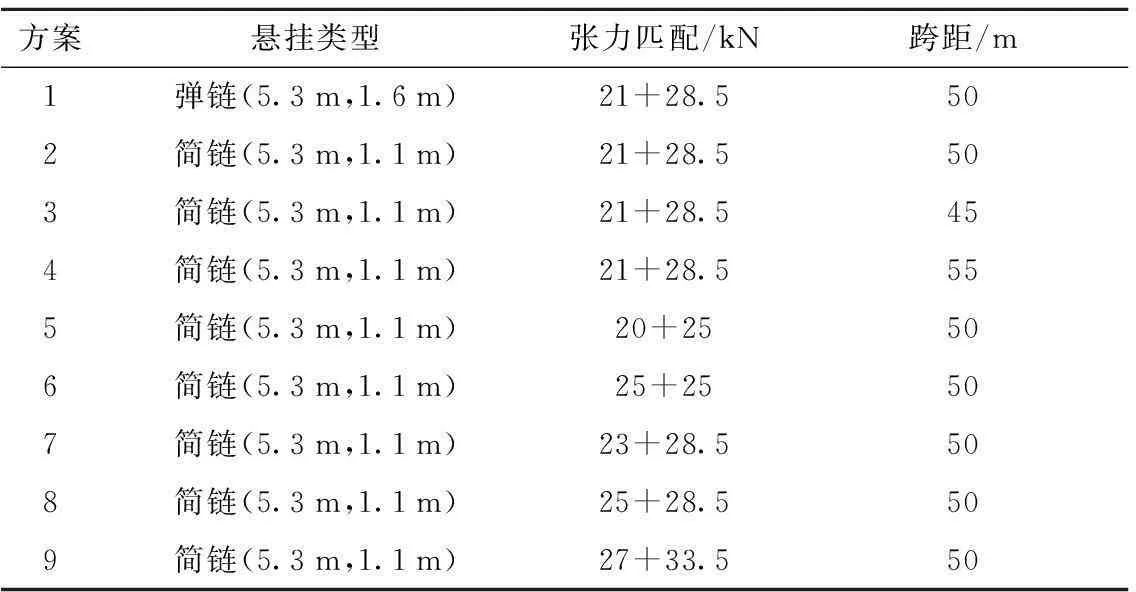
表3 接觸網(wǎng)組合方案
向抖振位移最大值,獲得接觸網(wǎng)在風(fēng)壓作用下的風(fēng)致振動位移最大值,疊加水平平均位移與水平抖振位移最大值,獲得接觸網(wǎng)在風(fēng)壓作用下的風(fēng)偏最大值,見表4。
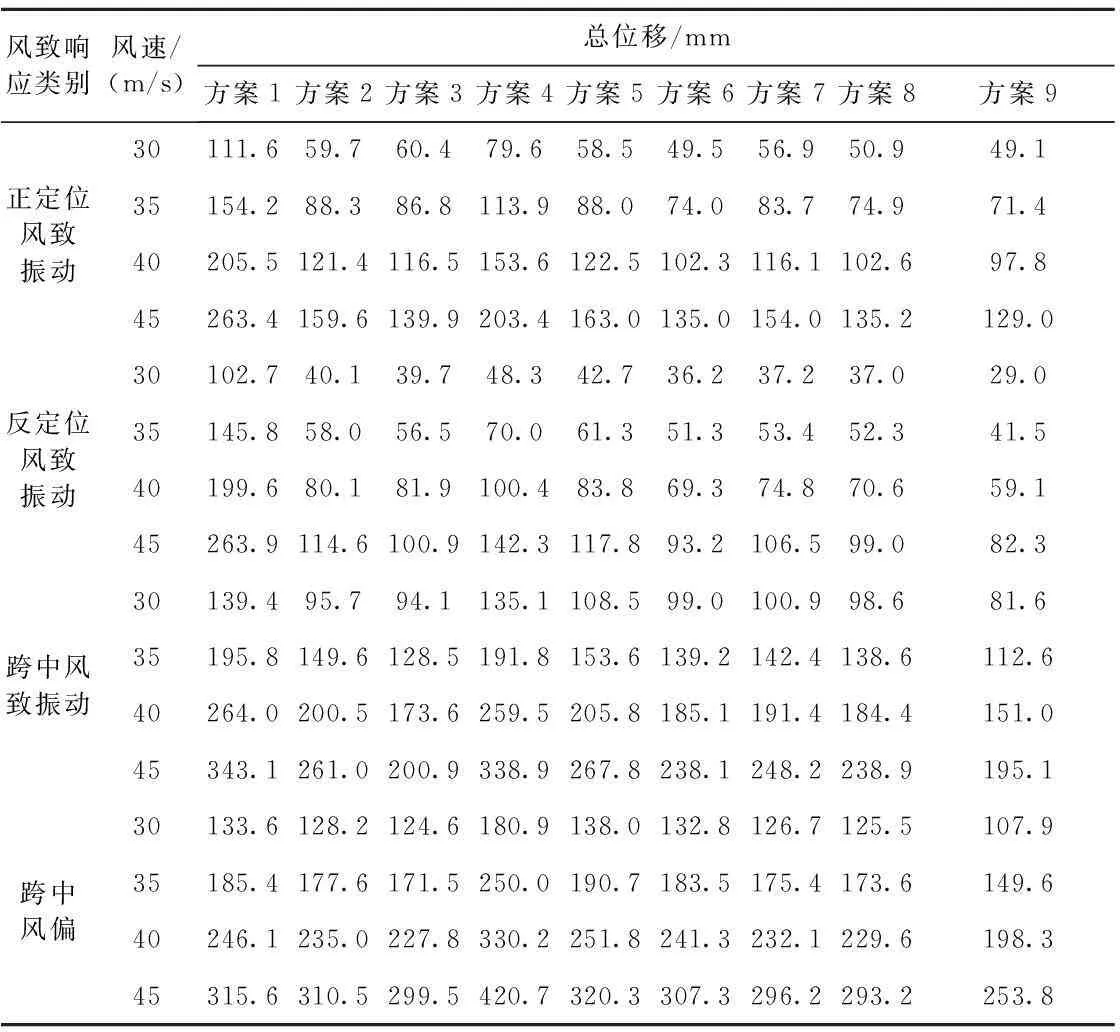
表4 接觸網(wǎng)風(fēng)致響應(yīng)計算結(jié)果
3.2 接觸網(wǎng)參數(shù)對風(fēng)致響應(yīng)的影響分析
圖4(a)、圖4(b)、圖4(c)分別所示為接觸網(wǎng)懸掛類型、跨距、張力對風(fēng)致響應(yīng)的影響,結(jié)合圖4及表4可以得出如下結(jié)論。
(1)與彈鏈相比,簡鏈整體剛度大,抗風(fēng)穩(wěn)定性較好。
(2)跨距由55 m減小至50 m,風(fēng)致響應(yīng)明顯減小。跨距由50 m減小至45 m,風(fēng)速不大于40 m/s時豎向位移變化較小,風(fēng)速大于40 m/s時,豎向位移有較大的變化量。從抗風(fēng)穩(wěn)定性角度考慮,跨距不應(yīng)大于50 m。
(3)承力索與接觸線的張力和越大,整體剛度越大,抗風(fēng)穩(wěn)定性越好;從風(fēng)致振動角度,對于設(shè)置擋風(fēng)結(jié)構(gòu)的工況,由于接觸線與承力索的高度不同,擋風(fēng)墻/屏后接觸線與承力索處的風(fēng)速變化系數(shù)不同且差別較大[19],具體差別詳見本文2.1節(jié),因此與增大接觸線張力相比,增大承力索張力對于抗風(fēng)穩(wěn)定性的提高更為敏感,張力對豎向位移約束作用由弱到強依次為20 kN+25 kN、21 kN+28.5 kN、23 kN+28.5 kN、25 kN+25 kN、25 kN+28.5 kN、27 kN+33.5 kN。此外,從風(fēng)偏角度,有必要適當(dāng)增大接觸線張力,以對風(fēng)偏形成更好的約束作用,張力對風(fēng)偏約束作用由弱到強依次為20 kN+25 kN、25 kN+25 kN、21 kN+28.5 kN、23 kN+28.5 kN、25 kN+28.5 kN、27 kN+33.5 kN。
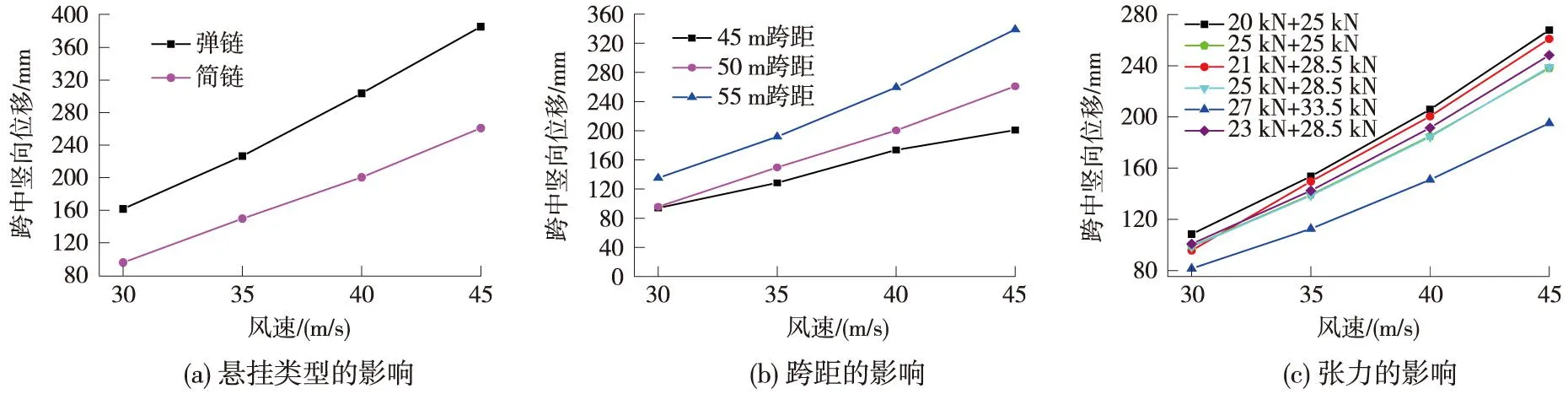
圖4 接觸網(wǎng)參數(shù)對風(fēng)致響應(yīng)的影響
4接觸網(wǎng)氣動彈性風(fēng)洞試驗
進行接觸網(wǎng)風(fēng)致響應(yīng)氣動彈性風(fēng)洞試驗,模擬接觸網(wǎng)結(jié)構(gòu)動力特性、評估接觸網(wǎng)系統(tǒng)風(fēng)致響應(yīng),與有限元計算結(jié)果進行對比、驗證。
經(jīng)振型、頻率計算及測試,有限元模型與風(fēng)洞試驗的振型一致、頻率誤差約5%,對比結(jié)果見表5。

表5 振型、頻率理論計算與風(fēng)洞實測對比結(jié)果
經(jīng)對比,接觸網(wǎng)風(fēng)致振動與風(fēng)偏的有限元計算結(jié)果與風(fēng)洞試驗結(jié)果基本吻合(圖5),接觸網(wǎng)參數(shù)對風(fēng)致響應(yīng)的影響的研究結(jié)果正確。
研究成果直接應(yīng)用于蘭新鐵路第二雙線大風(fēng)區(qū)接觸網(wǎng)系統(tǒng)方案設(shè)計和技術(shù)參數(shù)選擇中,為大風(fēng)區(qū)接觸網(wǎng)的防風(fēng)設(shè)計、工程建設(shè)提供了科學(xué)依據(jù)。并在工程實踐基礎(chǔ)上,此研究成果作為主要技術(shù)支撐之一,形成了首個國內(nèi)外鐵路電化行業(yè)標(biāo)準(zhǔn)《風(fēng)區(qū)200~250 km/h電氣化鐵路接觸網(wǎng)主要裝備技術(shù)條件(暫行)》(TJ/GD 002—2013)。
5結(jié)論
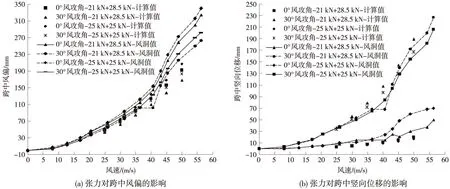
圖5 理論計算與風(fēng)洞試驗對比結(jié)果
本文采用有限元計算與接觸網(wǎng)氣動彈性風(fēng)洞試驗相結(jié)合的方法研究了接觸網(wǎng)的風(fēng)致響應(yīng)。在接觸網(wǎng)有限元模型中施加風(fēng)荷載作用,對不同接觸網(wǎng)參數(shù)的組合方案進行風(fēng)致響應(yīng)的定量計算,分析了懸掛類型、張力組合、跨距對接觸網(wǎng)風(fēng)致響應(yīng)的影響。并在國內(nèi)外鐵路電氣化行業(yè)首次開展了接觸網(wǎng)氣動彈性風(fēng)洞試驗接觸網(wǎng)氣動彈性風(fēng)洞試驗,試驗結(jié)果表明接觸網(wǎng)參數(shù)對風(fēng)致響應(yīng)的影響的研究結(jié)果可信,研究結(jié)論如下:
(1)與彈鏈相比,簡單鏈形懸掛抗風(fēng)穩(wěn)定性較好;
(2)跨距減小,風(fēng)致響應(yīng)相應(yīng)減小;從抗風(fēng)穩(wěn)定性角度,跨距不應(yīng)大于50 m;
(3)承力索與接觸線的張力和越大,抗風(fēng)穩(wěn)定性越好;從豎向位移角度,增大承力索張力對于抗風(fēng)穩(wěn)定性的提高更為敏感;從風(fēng)偏角度,有必要適當(dāng)增大接觸線張力。
本研究可應(yīng)用于具有抗風(fēng)穩(wěn)定性能需求的接觸網(wǎng)研究、設(shè)計以及工程實施等方面。
參考文獻:
[1]韓佳棟,曹樹森,劉曉紅,等.強風(fēng)地區(qū)接觸網(wǎng)風(fēng)振響應(yīng)分析[J].鐵道建筑技術(shù),2010(S):207-210.
[2]朱偉林,周全,羅偉.基于模擬脈動風(fēng)場的鐵路接觸網(wǎng)風(fēng)振響應(yīng)分析[J].機械與電子,2011(12):76-78.
[3]謝將劍,王毅,苑玉超,等.基于DIT-FFT優(yōu)化WAWS法的接觸網(wǎng)風(fēng)致響應(yīng)分析[J].空間結(jié)構(gòu),2013,19(2):63-69.
[4]曹樹森,柯堅,鄧斌,等.強風(fēng)地區(qū)接觸網(wǎng)動力穩(wěn)定性分析[J].中國鐵道科學(xué),2010,31(4):79-84.
[5]李瑞平,周寧,張衛(wèi)華.基于AR模型的接觸網(wǎng)脈動風(fēng)場與風(fēng)振響應(yīng)[J].交通運輸工程學(xué)報,2013,13(4):56-61.
[6]A. Collina, A. Facchinetti, F. Resta. A feasibility study of an aerodynamic control for a high speed pantograph[J]. IEEE international conference on advanced intelligent mechatronics, 2007(9):1-6.
[7]Sergio Avila-Sanchez, Oscar Lopez-Garcia, Jose Meseguer. Influence of Embankments with Parapets on the Cross-Wind Turbulence Intensity at the Contact wire of Railway Overheads[C]∥Proceedings of the 2010 Joint Rail Conference. Urbana : American Society of Mechanical Engineers, 2010:1-8.
[8]王之宏.風(fēng)荷載的模擬研究[J].建筑結(jié)構(gòu)學(xué)報,1994,15(1):44-52.
[9]張相庭.結(jié)構(gòu)風(fēng)壓和風(fēng)振計算[M].上海:同濟大學(xué)出版社,1985.
[10]黃本才.結(jié)構(gòu)抗風(fēng)分析原理及應(yīng)用[M].上海:同濟大學(xué)出版社,2001.
[11]中華人民共和國鐵道部.TB 10009—2005鐵路電力牽引供電設(shè)計規(guī)范[S].北京:中國鐵道出版社,2005.
[12]中華人民共和國交通部.JTG/T D60-01—2004公路橋梁抗風(fēng)設(shè)計規(guī)范[S].北京:人民交通出版社,2004.
[13]Panofsky H A, Mccormick R A. The spectrum of vertical velocity near the surface[J]. Quarterly Journal of the Royal Meteorological Society, 1960(86):546-564.
[14]Lumley J L, Panofsk H A. The structure of atmospheric turbulence[M]. New York: Wiley, 1964.
[15]丁泉順,陳艾榮,項海帆.大跨度橋梁空間脈動風(fēng)場的計算機模擬[J].力學(xué)季刊,2006,27(2):184-189.
[16]Simiu E, Scanlan R H.風(fēng)對結(jié)構(gòu)的作用-風(fēng)工程導(dǎo)論[M].劉尚培,項海帆,謝霧明,譯.上海:同濟大學(xué)出版社,1992.
[17]Davenport A G. The Application of Statistical Concepts to the wind Loading of Structures[C]∥Proc. ICE. London: American Society of Civil Engineers, 1961:449-472.
[18]胡曉倫.大跨度斜拉橋顫抖振響應(yīng)及靜風(fēng)穩(wěn)定性分析[D]. 上海:同濟大學(xué),2006.
[19]劉改紅.風(fēng)區(qū)擋風(fēng)墻/屏影響下接觸網(wǎng)設(shè)計風(fēng)速計算研究[J].鐵道標(biāo)準(zhǔn)設(shè)計,2013(9):90-93.
Influence of OCS Parameters on Wind-induced Response and Corresponding Wind Tunnel TestsLIU Gai-hong
(China Railway First Survey and Design Institute Group Co., Ltd., Xi’an 710043, China)
Abstract:Strong wind may induce bigger and more complicated vibration and deviation of the overhead line system (OCS), thus the influence of OCS parameters on the wind-induced response is to be studied to provide a scientific basis for anti-wind design of OCS in strong wind areas. Therefore, this paper firstly uses the commercial software ANSYS to build up a finite element analysis model that includes the support structures and suspension parts. Secondly, the method of weighted amplitude wave superposition (WAWS) is used to simulate the fluctuating wind field based on specific characteristics of the OCS. Furthermore, the suspension type, tension combination and the influence of span on wind-induced response are determined by quantitative analyses and calculating the displacement caused by wind induced response of different combination OCS under wind load. Also, corresponding wind tunnel tests are conducted. The test results show that the finite element calculation results match the measurements of the wind tunnel tests in terms of the displacements due to wind-induced response. This study results are employed to design catenary system and technical parameters in Lanzhou-Urumqi High-Speed Railway and create the first catenary equipment technical conditions for strong wind areas in railway electrochemical industry world wide.
Key words:OCS parameters; Wind-induced response; Wind tunnel test; Quantitative analyses; High-speed railway
中圖分類號:U225.4
文獻標(biāo)識碼:A
DOI:10.13238/j.issn.1004-2954.2016.02.030
文章編號:1004-2954(2016)02-0144-05
作者簡介:劉改紅(1983—),女,工程師,2009年畢業(yè)于清華大學(xué)機械工程專業(yè),工學(xué)碩士,E-mail:549497471@qq.com。
基金項目:鐵道部科技研究開發(fā)計劃項目(2010G019-G)
收稿日期:2015-06-05; 修回日期:2015-07-28

