基于捕食搜索策略的粒子群算法求解高鐵閉塞分區劃分問題

王　瑞，陳永剛

(蘭州交通大學自動化與電氣工程學院，蘭州　730070)

?

基于捕食搜索策略的粒子群算法求解高鐵閉塞分區劃分問題

王瑞，陳永剛

(蘭州交通大學自動化與電氣工程學院，蘭州730070)

摘要：高鐵閉塞分區的合理劃分可以保證列車的運行安全、提高運輸效率和減少投資成本。為了更好地解決這個問題，利用基于捕食搜索策略的粒子群算法求解優化準移動閉塞條件下的閉塞分區劃分模型。捕食搜索策略可以平衡粒子的局域搜索和全局搜索，從而避免陷入局部最優，提高算法精度。通過算例仿真，比較基于捕食搜索策略的粒子群算法和標準粒子群算法對模型優化的結果，驗證基于捕食搜索策略的粒子算法對模型的求解是有效的，而且得到的解更精確，運算速度更快。

關鍵詞：高速鐵路；捕食搜索策略；粒子群算法；閉塞分區；準移動閉塞

高速鐵路建設首先解決的是選線設計和閉塞分區的設計。目前，我國閉塞分區長度的確定大多以區間運行時間間隔進行劃分，這種劃分方式由于需留有較大的列車追蹤間隔，導致運行密度較低，運輸效率不高[1]。所以，研究鐵路閉塞分區的劃分問題，尤其是準移動閉塞制式下閉塞分區劃分問題，對于保證行車安全、提高線路通過能力和減少投資成本都具有重要意義。

目前，國外學者已經將啟發式的坡道搜索算法[2]、遺傳算法[3]、差分進化算法[4]、最大-最小蟻群算法[5]應用于地鐵系統的信號機布局優化。國外學者主要針對城市軌道交通系統的閉塞分區劃分問題進行了研究，沒有涉及干線鐵路。在國內，劉海東等人[6]實現了利用計算機建立仿真系統完成干線鐵路三顯示固定閉塞的信號機布置。劉劍峰等人[7]在分析了影響區間信號機布置因素后，建立了區間四顯示固定閉塞信號機布置優化模型，并用遺傳算法對模型進行了求解。國內學者雖然已將智能算法用于求解干線鐵路固定閉塞條件下閉塞分區劃分問題，但沒有系統地分析閉塞分區劃分的影響因素及其約束條件，約束條件較簡單。并且較少研究準移動閉塞條件下的閉塞分區劃分問題。再者其運用的算法存在編碼過程復雜、計算量大、極易陷入局部最優等問題。現在運用基于捕食搜索策略的粒子群算法實現高速鐵路閉塞分區的快速合理劃分，提高閉塞分區劃分的質量和速度。

1閉塞分區劃分模型

主要研究準移動閉塞制式下、列車運行控制系統為CTCS-2級的高鐵閉塞分區劃分方法，以閉塞分區劃分數量最少為優化目標，在滿足列車追蹤間隔時間和制動距離等因素的條件下進行閉塞分區劃分，最終在保證列車運行安全和一定效率的前提下，實現降低建設成本和減少線路維修工作量的目的。

本文用到的模型來自參考文獻[13]，為了提高計算精度，對模型中的部分參數進行了調整，并將文獻[13]模型中的第一接近信號點位置條件去掉，而在區間信號點位置條件中進行重新定義。

1.1　定義變量

假設Ⅰ站和Ⅱ站相鄰，兩站之間信號點的個數為N，每個信號點位置的坐標為xi(i=1，2，…，N)。I站的反向進站信號機坐標為x0，Ⅱ站的進站信號機坐標為xN+1。對應的閉塞分區的長度li(i=1，2，…，N+1)為相鄰兩個信號點坐標的差值。

1.2　目標函數

為了達到降低建設成本和減少維修工作量的目的，閉塞分區劃分數量在滿足一定效率的條件下要盡可能的少，這里設定列車追蹤間隔時間不大于H(3 min)。目標函數為

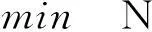
(1)

1.3　約束條件

約束條件如下所述。

(1)區間信號點位置

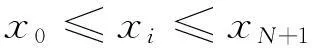
(2)

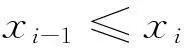
(3)

(2)閉塞分區長

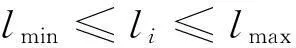
(4)

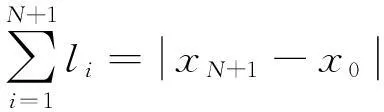
(5)

式中，li為閉塞分區長度；lmin為閉塞分區的最小長度；lmax為閉塞分區最大長度。

(3)閉塞分區劃分數量

閉塞分區劃分數量n(n=N+1)，其取值條件如下

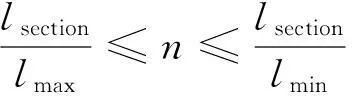
(6)

式中，lsection為Ⅰ站和Ⅱ站之間的區間長度。

(4)第一離去信號點位置

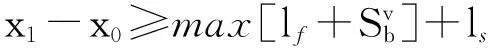
(7)

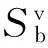
(5)第二接近信號點位置

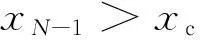
(8)

式中，xN-1為第二接近信號點坐標；xc為第二接近信號點下限位置(由進站間隔時間計算得到)。

(6)CTCS軌道電路正常碼序顯示

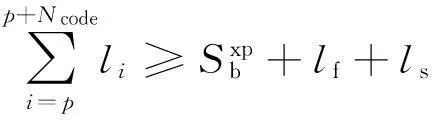
(9)

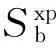
(7)停車起動條件

列車在每個信號點前停車以后再次起動需要滿足以下條件

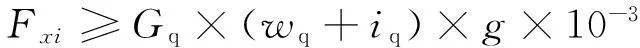
(10)

式中，Fxi為列車在xi位置處的起動牽引力；Gq為列車總重；wq為列車單位基本阻力；iq為xi位置處坡度千分數。

(8)列車追蹤間隔時間

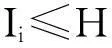
(11)

式中，Ii為列車追蹤間隔時間(閉塞分區劃分完畢后根據公式進行計算)；H為給定的列車追蹤間隔時間。

1.4　適應度函數

由于以閉塞分區劃分數量最少為優化目標即求目標函數的最小值。因此，適應度函數定義如下

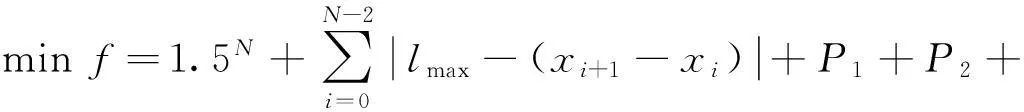
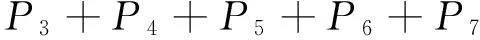
(12)

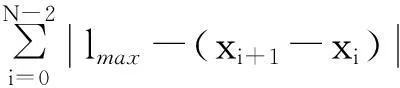
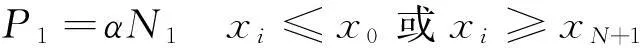
(13)

式中，P1與信號點限界位置有關；α為懲罰因子；N1為在給定范圍外的信號點個數。

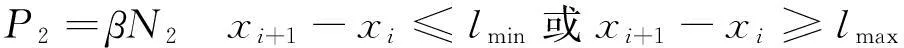
(14)

式中，P2與閉塞分區長度限值有關；β為懲罰因子；N2為分區長度在規定長度以外的個數。

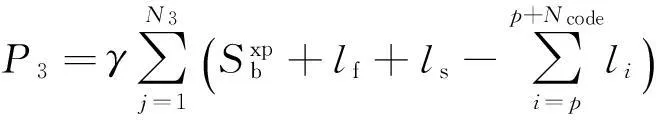
(15)

式中，P3與軌道電路碼序有關；γ為懲罰因子；N3為不滿足軌道電路碼序約束條件的閉塞分區個數。

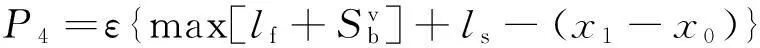
(16)

式中，P4與第一離去信號點位置有關；ε為懲罰因子；當滿足第一離去信號點條件時要減小個體適應度值。

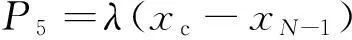
(17)

式中，P5與第二接近信號點位置有關；λ為懲罰因子；當滿足第二接近信號點條件時要減小個體適應度值。

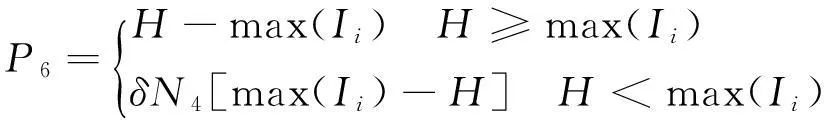
(18)

式中，P6與列車追蹤間隔有關；δ為懲罰因子；N4為大于給定列車追蹤間隔時間H的閉塞分區個數。

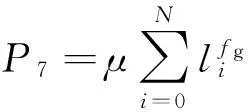
(19)

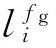
上面各式中的懲罰因子α、β、γ、ε、λ、δ、μ，根據懲罰強弱程度不同而取值不同，其取值在10～30。

2基于捕食搜索策略的粒子群算法(PSPSO)

2.1　粒子群算法

粒子群算法(Particle Swarm Optimization， PSO)是由Kennedy博士 和 Eberhart教授于1995年提出來的。PSO是一種隨機的、并行的優化算法。其算法簡單，容易實現，且不要求被優化函數具有可微、可導、連續等性質，收斂速度快。

假設在D維空間中求解，群體中有m個粒子，這些粒子在解空間中以一定的速度飛行，每個粒子都是一個可能的解， 都是一個D維向量，記作xi=(xi1，xi2，…，xiD)，即第i(i=1，2，…，m)個粒子在 D維的搜索空間中的位置是xi。將滿足設定的約束條件的xi帶入預設的適應度函數中，可以計算每個粒子的適應度值， 然后依據適應度值的大小判定xi的優劣。在搜索過程中，每個粒子根據自己搜索到的歷史最優位置和群體內或鄰域內其他粒子搜索到的歷史最優位置進行位置的變化。第i個粒子的速度也是一個D維向量，記作vi=(vi1，vi2，…，viD)，第i個粒子搜索到的歷史最好點記作pi=(pi1，pi2， …，piD)，整個群體搜索到的歷史最優點記作pg=(pg1，pg2，…，pgD)。粒子的位置和速度都是實數，其根據下面的方程進行變化

(20)

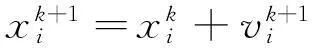
(21)

式中，c1和c2稱為學習因子或加速系數；ξ，η是在[0，1]區間內的均勻分布的偽隨機數；ω稱為慣性權重，是一個位于[0，1]區間內的常數；k為迭代次數。

2.2　捕食搜索策略

粒子群算法計算簡單、容易實現、收斂速度快，但是由于粒子交流信息量過大和信息流動的單一性，粒子就會加速聚集。隨著迭代的進行，粒子種群多樣性就會下降，迭代后期很難找到更好的解，容易陷入局優。使得算法對復雜問題的開發能力減弱。為了解決這個問題將捕食搜索策略引入到標準粒子群算法中。

捕食搜索(Predatory Search， PS)是由巴西學者Alexandre Linhares在1998年提出來的一種用于解決組合優化問題的模擬動物捕食行為的空間搜索策略。捕食搜索策略的思想：在整個解空間內進行全局搜索，找到一個較優解，然后在找到的較優解的周圍進行局域搜索，在進行多次搜索后，未發現更好的解，放棄局域搜索，轉到全局搜索。經過這樣多次循環最終找到最優解。由于大部分搜索時間都在較優解附近的較小區域進行搜索，所以搜索高效且速度快。將其引入到標準粒子群算法中，第一可以提高算法前期的迭代搜索能力，抑制早熟；第二可以提高算法的后期搜索能力找到更精確的解。

2.3　基于捕食搜索策略的粒子群算法

在把捕食搜索策略引入到標準粒子群算法過程中，首先將限制定義為多維解空間內的兩點間的距離。粒子在某限制下的鄰域定義為與粒子的距離小于該限制的多維空間。在解空間內設置NL級限制：R(1)，R(2)，…，R(NL)。

在最小限制R(1)規定的鄰域內隨機初始化m個粒子，根據標準PSO公式迭代若干次，試圖找到更優解，當PSO進行Cs次還不能找到，則增加限制到R(2)，在其鄰域內初始化粒子群，根據公式迭代，若能找到則替換歷史最優解，并重新計算限制，若不能則繼續增加限制等級，隨著限制等級的增加搜索空間也在增大。當限制等級達到某一個值Ls時，而無法找到更優解時，就需放棄區域搜索，將搜索限制增加到一個較高的等級Lh，也就跳出了局部最優，如此循環，直到設定的限制等級NL規定的鄰域也搜索完成。

重新計算限制方法如下：

(1)在初始解空間利用標準粒子群算法搜索NL次，得到NL個解；

(2)把這NL個解按照到發現的歷史最優解的距離從小到大排列，組成NL級限制。

算法主要步驟如下：

步驟1在解空間內隨機選擇一個解x，令其為歷史最優解pg，pg=x，PSO進行次數k=0，限制等級L=1；

步驟2若L≤NL，在x的R(L)限制內初始化m個粒子，粒子的最大速度為當前限制，按照公式(19)、公式(20)迭代若干次，找到其歷史最優解p，然后轉到步驟3，否則結束；

步驟3令x=p，解x的適應值與歷史最優解pg的適應值進行比較，若f(x)

步驟4令k=k+1，若k≤Cs，則轉步驟2，否則令L=L+1，轉步驟5；

步驟5若L=Ls，則令L=Lh，轉步驟2，否則直接轉步驟2。

3算例分析

3.1　數據準備

以Ⅰ站—Ⅱ站區間為待劃分區間，Ⅰ站中心公里標為0 km，反向進站信號機公里標為1 km，Ⅱ站中心公里標為34.500 km，進站信號機公里標為33.500 km，區間全長33.5 km。參數條件如表1所示。

表1　閉塞分區劃分參數

軌道電路傳輸極限長度如表2所示。

表2　軌道電路傳輸極限長度

所選用的動車組類型及其參數如表3所示。

表3　區間運行動車組類型及參數

3.2　算法參數設置

在PSPSO中，通過限制L來實現全局搜索和局部搜索的平衡，學習因子和慣性權重只在內循環中起作用，對全局和局域搜索影響不大。因此，學習因子和慣性權重可以采用固定值，本文令c1=c2=1，ω=0.5。另外，粒子數取10，在Matlab中經過多次仿真后將一些參數做如下設置：NL=N，Cs=N，Ls=[NL/4]，Lh=NL-Ls。

3.3 計算結果及分析

利用Matlab對算法進行仿真驗證。根據公式(6)得到可劃分的閉塞分區數量范圍，進而得到區間布置的信號點數量N的范圍，根據N由小到大依次進行尋優。經過仿真求解，當N=13時，得到最優布置結果。圖1為N=13時的歷史最優解的適應度函數值隨循環次數變化而變化的關系曲線，得到一次歷史最優解pg為一次循環，粒子的迭代次數取10。

圖1　算法適應度隨迭代次數變化曲線

從圖1可知，PSPSO算法在循環到第104次左右收斂，總循環次數為10×104=1 040代左右收斂，并找到了比較優良的結果。

為了進一步說明算法的優越性，本文將標準PSO算法和PSPSO算法分別運行30次，結果對比如表4所示。

表4　PSPSO和標準PSO優化比較

由于標準PSO算法在粒子數為10時，很難找到最優解，因此，將粒子數增大到100。從表4可知，雖然標準PSO算法收斂速度比較快，但是不能保證每次都收斂到最優，可能收斂到局優。實際上標準PSO算法隨著迭代的進行，認識部分和學習部分在減小， 粒子的種群多樣性下降，容易陷入局優。而PSPSO算法搜索時每次都會重新初始化粒子，由于不會受歷史信息的影響，用較少的粒子也不會陷入局優。而在計算時間上，雖然PSPSO算法的迭代次數要多一些，但是由于粒子數量少，搜索所用的時間反而更短。

PSPSO算法優化最終得到的信號點布置結果如表5所示。從表5的優化結果得知，閉塞分區的最大長度為2 830 m，符合最大長度要求。區間的最大列車追蹤間隔為2.14 min，符合給定的追蹤間隔(3 min)要求，經檢驗，車站追蹤間隔也符合要求。最大碼序為U，符合碼序檢驗要求。綜上說明，算法是有效的。

表5　基于捕食搜索策略粒子群算法的優化結果

布置同樣長度的區間，最終得到的結果與文獻[13]相比，劃分的閉塞分區個數都為13個，區間的最大列車追蹤間隔時間2.14 min，優于文獻[13]得到的2.2 min，在閉塞分區個數相同的情況下，本文的劃分結果在效率方面優于文獻[13]。

4結語

利用基于捕食搜索策略的粒子群算法求解優化高鐵閉塞分區劃分模型?；诓妒乘阉鞑呗缘牧Ｗ尤核惴ɡ幂^少的粒子，通過限制等級的調節，實現快速收斂到全局最優。通過實例仿真驗證了基于捕食搜索策略的粒子群算法求解高鐵閉塞分區劃分問題是有效的。算法在重新計算限制時，是通過隨機初始化粒子群實現的，這樣可能會出現較差的解，減慢算法的收斂速度，有待改進。

參考文獻：

[1]王瑞峰，高繼祥.鐵路信號運營基礎[M].北京:中國鐵道出版社，2008.

[2]Gill D C， Goodman C J. Computer-based optimisation techniques for mass transit railway signalling design[C]. IEE Proceedings B (Electric Power Applications). IET Digital Library， 1992，139(3):261-275.

[3]Chang C S， Du D. Improved optimisation method using genetic algorithms for mass transit signalling block-layout design[C]. Electric Power Applications， IEE Proceedings-IET， 1998，145(3):266-272.

[4]Chang C S， Du D. Further improvement of optimisation method for mass transit signalling block-layout design using differential evolution[C].Electric Power Applications， IEE Proceedings-IET， 1999，146(5):559-569.

[5]Ke B R， Chen M C， Lin C L. Block-layout design using MAX-MIN ant system for saving energy on mass rapid transit systems[J]. Intelligent Transportation Systems， IEEE Transactions on， 2009，10(2):226-235.

[6]劉海東，毛保華，劉劍鋒，等.鐵路信號機布置及其計算機實施系統研究[J].系統仿真學報，2006，18(1):62-66.

[7]劉劍鋒，毛保華，侯忠生，等.基于遺傳算法的區間自動閉塞信號機布局優化方法[J].鐵道學報，2006，28(4):54-59.

[8]衛和君.鐵路自動閉塞分區劃分技術展望[J].長沙鐵道學院學報，2003，21(4):99-102.

[9]王俊偉.粒子群優化算法的改進及應用[D].東北大學，2006.

[10]劉冬華，甘若迅，樊鎖海，等.基于捕食策略的粒子群算法求解投資組合問題[J].計算機工程與應用，2013，49(6):253-256.

[11]張濟民，吳汶麒.準移動閉塞列車安全間隔時間的計算[J].鐵道學報，1999，21(3):6-10.

[12]潘峰，李位星，高琪，等.粒子群優化算法與多目標優化[M].北京:北京理工大學出版社，2013.

[13]劉海東，毛保華，王保山，等.基于差分進化算法的高速鐵路區間信號布置優化方法研究[J].鐵道學報，2013，35(5):40-46.

Particle Swarm Algorithm Based on Predatory Search Strategy for Partitioning of High-speed Railway Block Section

WANG Rui， CHEN Yong-gang

(School of Automation and Electrical Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China)

Abstract：The rational division of the high-speed railway block section serves to ensure safe traffic， improve transport efficiency and reduce investment. In this regard， the new optimization model of block section in the quasi-moving block is solved with particle swarm optimization algorithm based on predatory search strategy. The predatory search strategy balances local search and global search of the particles， so as to avoid local optimum and improve algorithm accuracy. By numerical example and comparing the optimization results of the particle swarm algorithm， the effectiveness of the particle swarm algorithm is validated based on the predatory search strategy for solving the model with more precise solutions are and faster operation speed.

Key words：High-speed railway; Predatory search strategy; Particle swarm algorithm; Block section; Quasi-moving block

作者簡介：王瑞(1989—)，男，碩士研究生，E-mail:393556335@qq.com。

基金項目：國家自然科學基金地區項目(61164101)

收稿日期：2015-05-08； 修回日期：2015-06-14

中圖分類號：U238； U284

文獻標識碼：ADOI:10.13238/j.issn.1004-2954.2016.01.029

文章編號：1004-2954(2016)01-0131-05