應用電各向異性介質電多極展開計算電勢

李文略(嶺南師范學院基礎教育學院，廣東 湛江 524037)

應用電各向異性介質電多極展開計算電勢

李文略?
(嶺南師范學院基礎教育學院，廣東 湛江 524037)

應用張量分析的矩陣方法得到電各向介質中多極展開式在主軸坐標系下的具體形式。應用該具體形式結合廣義坐標變換法計算均勻帶電圓盤、橢圓盤、橢圓環、圓環和旋轉橢球在電各向異性介質中遠場的電勢，所得的結果在ε22=ε33=ε的情況下，可過渡到在電各向同性介質中遠場的電勢。

電各向異性介質；電勢；電多極展開；張量；橢圓盤；旋轉橢球

1 引言

電各向同性介質靜電場的求解方法很多，如分離變量法、電像法、格林函數法、電多極展開法等等。陳燊年[1]等系統的研究了電各向異性介質（限于有且只有三個正交主軸方向的電介質）的靜電場，其中有應用分離變量法和電多極展開法有效的求解了電各向異性介質中的靜電場。李洲圣，唐長紅[2]系統的定義了張量分析的矩陣方法，文[3-4]應用該方法研究了電（磁）各向異性介質的電磁場。本文將在前人研究[1、5]的基礎上，應用張量分析的矩陣方法推導得到電多極展開式在主軸坐標系下的具體形式，進而應用該具體形式結合廣義坐標變換法計算電各向異性介質中均勻帶電圓盤、圓環、橢圓盤、橢圓環和旋轉橢球等典型的連續帶電體在遠場處激發的電勢，可作為應用電多極展開式計算電勢的補充。

2 各向異性介質中電多極展開式的具體形式

在電各向異性介質中在主軸坐標系321xO- 下，坐標原點建在源區，當電荷系統分布在小區域內，在遠處產生的電勢多極展開式為[1、5]

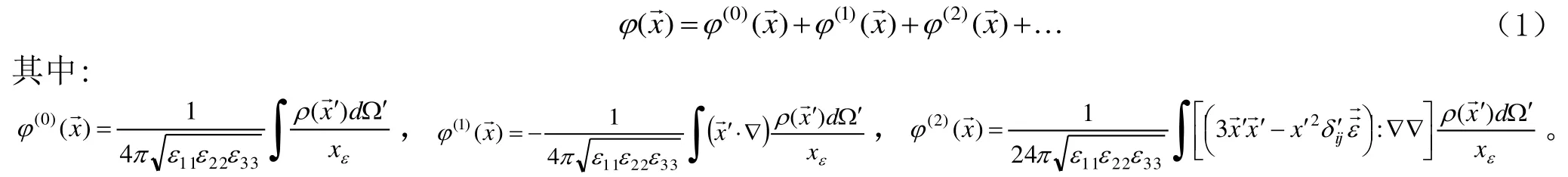
式中: x→、x′→分別表示場點和源點的位矢)(x′→ρ、Ωd 分別表示源電荷密度和源電荷體積元；)0(φ、)1(φ 和)2(φ分別稱為電零極項、電偶極項和電四極項；，11ε 、22ε、33ε為沿著主軸坐標系中:

設電各向異性介質的主軸坐標系O-x1x2x3，記為的轉置形態，它們均表示同一坐標系。現應用張量分析的矩陣方法計算φ(1)（x）和φ(2)（x）在主軸坐標系下的具體形式。三個坐標軸正方向的介電常數。在實際中用得較多的通常只到)2(φ，因而本文涉及的計算也到)2(φ 為止。)2(φ 項

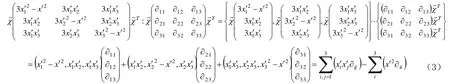
將式（2）（3）代入式（1）中，由多元函數二階偏導數及鏈式法則，可得

式（4）（5）（6）即為電各向異性介質中電多極展開在主軸坐標系下的具體形式。若令ε22=ε33=ε代入式（4）（5）（6）中，則可得到電各向同性介質中電多極展開的具體形式。應用具體形式結合廣義坐標變換法可直接方便的計算連續帶電體系在遠場處的電勢，而無需求解電偶極矩或電四極矩以及進行張量的多重點積運算.以下應用該具體形式直接計算典型連續帶電體遠場處的電勢。

3 電各向異性介質中均勻帶電圓盤、圓環遠場處的電勢

均勻帶電面密度為σ，電量為Q，半徑為R圓盤放置在主軸坐標系 O-x1x2x3（原點在圓盤中心）的 O -x1x2面上，應用具體形式求其在遠場點 P()處的電勢。

若此圓盤變為半徑為R的圓環，帶電線密度為λ，電量為Q，取極坐標r、θ，則 x1′ =Rcosθ、x ′2=R sinθ，

4 電各向異性介質中均勻帶電橢圓盤、橢圓環遠場處的電勢

4.1 均勻帶電橢圓盤遠場處的電勢

均勻帶電面密度為σ，電量為Q，長、短半軸為a、b的橢圓盤放置在主軸坐標系321xxxO- （原點在橢圓盤中心，長半軸沿著1x軸）的21xxO- 面上，應用具體形式求其在遠場點),,(321xxxP 處的電勢。

若令 Rba == （橢圓盤變為半徑為R的圓盤），代入式（11）中可得圓盤在遠場激發的電勢，結果與式（8）一致，藉此可驗證用多極展開具體形式計算遠場電勢的正確性.

4.2 均勻帶電橢圓環遠場處的電勢

帶電線密度為λ，電量為Q，長、短半軸為a、b的橢圓環，放置在主軸坐標系321xxxO- （原點在橢圓環中心，長半軸沿著1x軸）的21xxO- 面上，應用具體形式求其在遠場點 ),,(321xxxP 處的電勢.在環面上取廣

若令 Rba == 代入式（12）中，即可得均勻帶電圓環在遠場的電勢，如果與式（9）相同.

5 電各向異性介質中均勻帶電旋轉橢球遠場處的電勢

均勻帶電密度為ρ，電量為Q，長、短半軸為a、b的橢球，主軸坐標系 O - x1x2x3的原點在球心，長半軸沿著x3軸，應用電多極展開的具體形式求其在遠場點 P ( x1, x2,x3)處的電勢。

橢球電荷分布關于x1軸、 x2軸和 x3軸對稱，故(P)=0，且由式（6）得

6 結語

文[1、5]應用電多極展開式計算電各向異性介質的靜電場時，需先求出電多極矩，然后再進行（矢量）張量間的多重點積運算。本文應用電多極展開式的具體形式結合廣義坐標變換法可方便的計算均勻帶電圓盤、圓環、橢圓盤、橢圓環和旋轉橢球在遠場處電勢，計算的過程充分的利用電荷對稱分布的條件簡化了計算，也避免了求電多極矩、進行（矢量）張量間的多重點積和涉及橢圓積分的繁瑣運算，可作為現有應用電多極展開求解電各向異性介質中靜電場的補充。在令ε22=ε33=ε的情況下，所得的結果適用于電各向同性介質中的靜電場。

[1] 陳燊年, 洪清泉, 王建成.介質為各向異性的電磁場[M]. 北京: 科學出版社, 2012.

[2] 李洲圣, 唐長紅. 三維空間張量分析的矩陣方法[M]. 北京: 航空工業出版社, 2010.

[3] 李文略. 各向異性磁介質中ζ空間與χ空間的變換關系及應用[J]. 廣西物理, 2015, 36(2): 20-23.

[4] 李文略. 電各向異性介質中泊松方程的具體形式[J]. 泉州師范學院學報, 2015, 33(2): 93-96.

[5] 郭震寧, 陳燊年. 在各向異性介質中電勢的多極矩展開[J]. 華僑大學學報(自然科學版), 1993, 14(4): 440-446.

[6] 袁德榮. 球張量的多極展開法[J]. 湖北大學學報(自然科學版), 1988, (1): 94-98.

O441.1

A

1003-7551(2016)01-0025-04

2015-12-20

?通訊作者：physics2009ed@126.com