論力的功與力矩功之間的邏輯關系*
陳亞琦,蔣純志(湘南學院電子信息與電氣工程學院, 湖南 郴州 423000)
論力的功與力矩功之間的邏輯關系*
陳亞琦?,蔣純志
(湘南學院電子信息與電氣工程學院, 湖南 郴州 423000)
討論了力的功與力矩功之間的邏輯關系,通過討論分析明確了力矩功是力的功在轉動形式中的引申,當物體繞參考點做圓周運動時,力的功就是力矩功,否則,力的功不等于力矩功。
力的功;力矩 ;力矩功
1 引言
經典力學是一門以力的概念和定義為邏輯起點,以與之相關的定律(定理)為主線的理論體系。在這個體系內,概念的定義之間,都有嚴密的邏輯關系,即以力為邏輯起點的定量的因果律和嚴密的數學方程式化[1]。功是描述外力在物體位移過程中的空間累積效應,是能量變化的一種量度。在許多大學物理教材[2-4]中,先給出力做功的概念,然后從剛體定軸轉動引出力矩功的概念,從力矩功的推導過程看,力做的功就是該力矩的功。但學生在實踐中,發現力矩功為零時,力的功卻不一定為零,學生對此感到困惑不解。本文將從功的定義式出發,詳細討論力的功與力矩功之間的邏輯關系,讓學生從本源上理解這兩個概念的異同。
2 理論分析
2.1 質點相對參考點做圓周運動
如圖1所示,一質量為m的質點在力F的作用下,繞參考點O做圓周運動。t時刻dt時間內,質點m 在 P處發生微小位移 vd t ,根據功的定義[2]:力的元功等于力F與受力質點無窮小位移d的標積,所以即質點相對參考點做圓周運動時,力F的功與力F相對參考點的力矩功完全一樣,力產生的效果使物體發生了轉動,力F的功是質點繞O點轉動動能大小的量度。
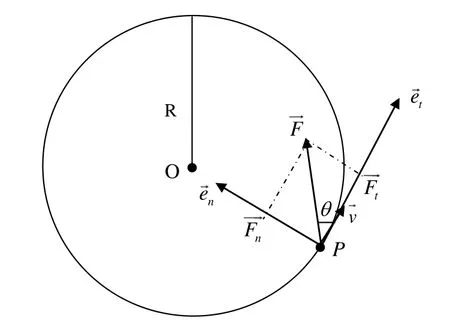
圖1 圓周運動分析圖
2.2 質點相對參考點做非圓周運動
如圖2所示,質點m在力F作用下繞參考點O做一橢圓運動。以方向為法向方向,建立自然坐標系,把質點運動分解成繞O點的轉動及在法向方向的移動兩種分運動,則質點在P處發生微小位移 vd t時,力F所作的功為:
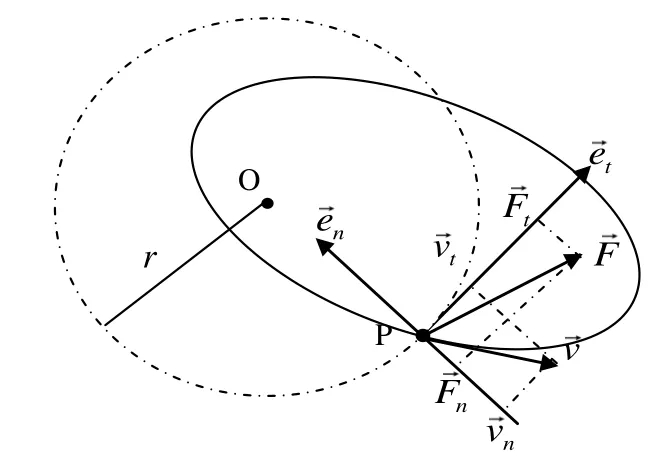
圖2 非圓周運動分析圖
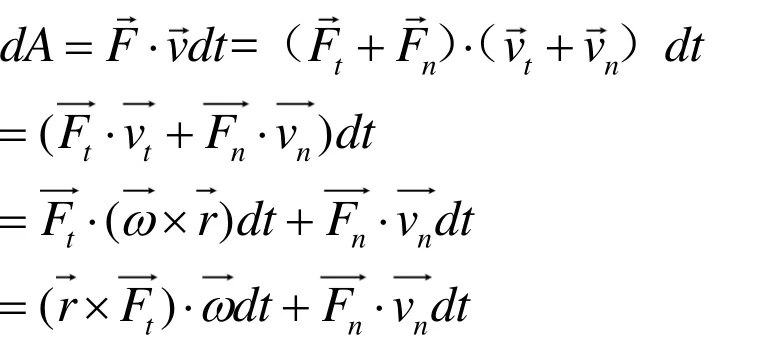
2.3 剛體平面運動
剛體作平面運動時,剛體上每一質點的運動狀態都可分解為隨質心的平動與繞質心軸的轉動。如圖 3所示,設力作用于作平面運動的剛體上的第i 個質點,由圖可知,第i 個質點的位置矢量為所以第i 個質點的元位移為,根據功的定義式,可知力iF對剛體做的元功為:
式中ω為質點i繞C點轉動的角速度。通過分析,我們可以發現力對剛體作的功可分解為兩個部分:式中第一項表明剛體質心平動動能的變化量;式中第二項表明剛體繞質心軸轉動的轉動動能的變化量,即力相對質心軸的力矩功。若剛體質心相對參考點的位移為零,則剛體繞質心軸做定軸轉動,這時力的功就是為力矩功。
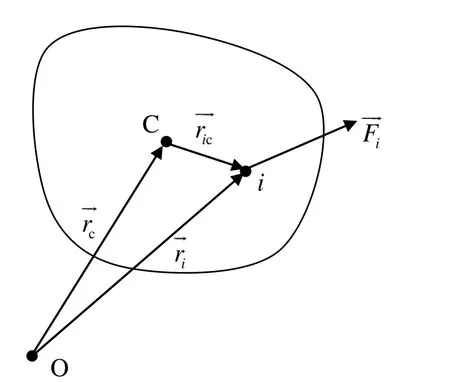
圖3 剛體平面運動
3 實例分析
常見實例:光滑桌面上有一質量為m的質點,拴在一根穿過桌面光滑小孔的繩子上。初始時,該質點離中心距離為r0,并以角速度ω0旋轉,現向下拉繩,使質點的徑向距離減少,質點從r0變到r0/2繼續旋轉,求拉力作的功。
分析:當質點的徑向距離逐漸減少時,質點繞圓孔的運動是非圓周運動,拉力的功與拉力相對圓孔參考點的力矩功不相等。
解法一:利用動能定理求解。質點m所受繩子拉力相對小孔的力矩始終為零,所以拉力矩的功為零,角動量守恒,有
解法二:利用功的定義式求解。設質點m由r0非常緩慢地漸變到,繩子的拉力也隨之逐漸增加,由角動量守恒定律及繩子拉力提供向心力,可得。根據功的定義式,計算拉力功
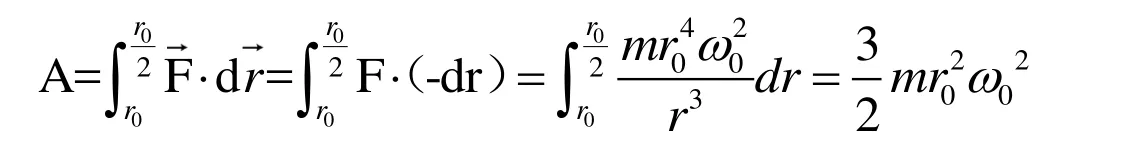
式中拉力使質點m沿矢徑方向靠近O點的效果,所以雖然力矩功為0,但拉力的功不為0。
4 結論
力對物體有移動效應,也有使物體繞某點轉動的效應,力矩是物體轉動效應的量度。功是描述力在物體位移過程中的空間累積效應,是能量變化的一種量度。當力使物體相對參考點做圓周運動時,力的功等于力矩功;當力使物體相對參考點的運動僅有矢徑方向上的平動時,該力相對參考點力矩的功為零,但力的功不為零;當力使物體相對參考點的運動既有轉動,也有徑向方向上的平動,則力的功為力矩功與物體相對參考點方向發生移動效應的所做功兩部分之和,力的功不等于力矩功。力的功是物體動能變化的量度,力矩功是轉動動能變化的量度,是力的功在轉動運動形式中的引申。
[1] 張立新. 物理學中的演繹邏輯[J]. 江蘇教育學院學報(自然科學版), 2013, 29(5): 42-45.
[2] 漆安慎, 杜嬋英. 普通物理學教程-力學[M]. 北京: 高等教育出版社, 2004: 113-184.
[3] 趙凱華, 羅蔚茵. 力學[M]. 北京: 高等教育出版社, 1995: 211-214.
[4] 程守珠. 普通物理學(第六版)(上冊)[M]. 北京: 高等教育出版社, 2006: 120-122.
O4-0
A
1003-7551(2016)01-0040-03
2015-1-20
湖南省教改項目(湘教通【2015】291-487);湖南省教育廳教改項目(編號:2013-223-452)
? 通訊作者:chenyaqi_0@163.com

