基于間歇控制的帶有時滯與非時滯線性耦合的復雜動力學網絡的完全同步

高俊

（江西財經職業學院，江西九江332000）

基于間歇控制的帶有時滯與非時滯線性耦合的復雜動力學網絡的完全同步

高俊

（江西財經職業學院，江西九江332000）

研究了帶有時滯與非時滯線性耦合的復雜動力學網絡的完全同步，設計出周期性間歇控制器，使得該系統同步于一個給定的軌道，得到了實現同步的標準，并運用數值模擬證明了理論結果的有效性。

復雜動力學網絡；時滯與非時滯線性耦合；間歇控制；完全同步

1中，S.Zheng等人研究了脈沖控制的帶有時滯與非時滯線性耦合的復雜動力學網絡的同步問題；在參考文獻2中，W.Guo等人研究了牽制控制的帶有時滯與非時滯線性耦合的復雜動力學網絡的同步問題；參考文獻3中，Z.Wang等人研究了自適應牽制控制的帶有時滯與非時滯線性耦合的復雜動力學網絡的同步問題；在參考文獻4中，S. Wen等人中研究了自適應牽制控制的帶有時滯與非時滯線性耦合的復雜動力學網絡的同步問題。

盡管如此，采用間歇控制的方法研究帶有時滯與非時滯線性耦合的復雜動力學網絡的同步問題，卻很少被提及。因此，本文采用間歇控制的方法研究帶有時滯與非時滯線性耦合的復雜動力學網絡的同步問題。

2 基本引理

引理1：（見參考文獻5）對于任意的正定矩陣Q∈Rn×n及向量x，y∈Rn，有2xTy≤xTQx+yTQ-1y。

引理2：（見參考文獻6、7、8）假設當t∈(-τ，∞)時y(t)是非負的連續函數，γ1，γ2，γ3為常數，γ1＞γ2＞0，，其中的唯一正解，且

3 模型建立

由N個相同的動力節點組成的帶有時滯與非時滯線性耦合的復雜動力學網絡：

選擇合適的間歇控制器使得網絡(1)同步到某個特定的軌道s(t)，使得這個s(t)是網絡（1）的孤立點的滿足s′(t)=f(s(t))的解，可能是一個循環軌道或是一個周期軌道，甚至可能是一個混沌軌道。

受控網絡

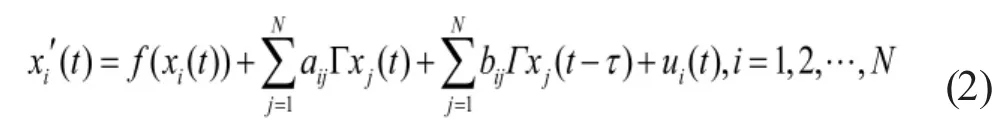
通過選擇適當的K，T，δ使得網絡（1）同步于給定的軌道s(t)。

令ei(t)=xi(t)-s(t)為同步誤差為控制率，則有誤差系統

4 理論證明

假設（A1）：假設存在常數Lf＞0，對于任意的x, y∈Rn及t＞0，有，其中

定理：如果存在正定矩陣P＞0，常數α，β，γ，η＞0，γ1＞γ2＞0，γ1+γ3＞0，且滿足下列條件：

因此，網絡（2）達到指數同步。

5 數值模擬

由6個相同的Chen系統節點構成的復雜動力學網絡如下描述：

為了使此復雜動力學網絡中的所有節點同步于一個給定的軌道s(t)（初始值為s(0)=(1,2,3)T的Chen吸引子，如圖1所示），選擇數據：控制增益矩陣K=10I3，控制周期T=1，控制寬度δ=0.4，控制率θ=δ/T=0.4，初始的狀態變量值任取。圖2中顯示了同步誤差。

圖1 Chen吸引子

圖2 同步誤差

參考文獻

[1]S.Zheng，G.Dong and Q.Bi.Impulsive synchronization of complex networks with non-delayed and delayed coupling[J].Phys.Lett.A, 2009,373(46):4 255-4 259.

[2]W.Guo，F.Austin，S.Chen and W.Sun.Pinning synchronization of the complex networks with non-delayed and delayed coupling[J]. Phys.Lett.A，2009,373(17):1 565-1 572.

[3]Z.Wang,L.Huang，Y.Wang and Y.Zuo.Synchronization analysis of networkswith both delayed and non-delayed couplings via adaptive pinning control method[J].Commun.Non.Sci.Numer.Simulat.，2010,15(12):4 202-4 208.

[4]S.Wen，S.ChenandW.Guo.Adaptiveglobalsynchronizationofageneral complexdynamicalnetworkwith non-delayed and delayed coupling[J]. Phys.Lett.A，2008，372(42):6340-6346.

[5]E.N.Sanchez and J.P.Perez.Input-to-State Stability(ISS)Analysis for Dynamic Neural Networks[J].IEEE Trans.Circuits Syst.I: Fundam.Theory Appl.,1999,46(11):1 395-1 398.

[6]S.Cai，J.Hao and Q.He.New results on synchronization of chaotic networks with time-varying delays via intermittent control[J]. Nonlinear Dynamics,2011,67(1)：393-402.

[7]S.Cai，Q.He，J.Haoand Z.Liu.Exponentialsynchronization ofcomplex networkswith nonidentical time-delayed dynamicalnodes[J].Physics LettersA，2010，374(25)：2 539-2550.

[8]S.Cai，J.Hao，Q.Heand Z.Liu.Exponentialsynchronization ofcomplex delayed dynamical networks via pinning periodically intermittent control[J].Physics LettersA，2011,375(19):1 965-1971.

（編輯：賈娟）

Exponential Synchronization of Complex Network with Non-delayed and Delayed Coup ling Via Interm ittent Feedback control

Gao Jun
(Jiangxi Vocational College of Finance and Econom ics,Jiujiang Jiangxi 332000)

This paper investigates the exponential synchronization of complex network with non-delayed and delayed coupling.A periodically intermittent controller is designed to synchronize the network onto a given orbit.The criteria for exponential synchronization are derived.Numerical simulation is presented to verify the effectiveness of the derived results.

complex dynamicalnetworks;non-delayed and delayed coupling;intermittent feedback control;exponential synchronization

TP271

A

2095-0748(2016)24-0079-03

10.16525/j.cnki.14-1362/n.2016.24.33

1 研究背景介紹

2016-11-15

高?。?987—），男，江西九江人，碩士，江西財經職業學院教師，主要研究方向：應用統計學、復雜動力學網絡。

復雜動力學網絡作為一門熱門學科被廣泛研究。復雜動力學網絡的同步行為是一種非常重要的動力學行為。間歇控制是一種非連續的控制方法，并且具有一定的控制寬度。由于它的方便與高效，間歇控制在通訊、運輸、生產等各個行業被廣泛使用。