樹狀管網和環狀管網水力計算研究

李軍霞（定西市安定區水務局，甘肅定西743000）

?

樹狀管網和環狀管網水力計算研究

李軍霞
（定西市安定區水務局，甘肅定西743000）

摘要：對中外學者提出的相關公式對管段流量、管道直徑、管網水頭損失進行詳細分析，旨在為管網水力計算的方法及灌溉管網設計的研究取得更大進展。節水灌溉管網水力計算是發展節水農業的重要途徑，在工程資金投入有限的情況下,進行管網系統的優化設計、尋求能滿足水量和水壓要求,且能使整個系統的造價最低或年費用最小、系統可靠性最高的設計方案,對節約投資、降低能耗、提高經濟效益和社會效益有著重要的現實意義。以節水灌溉管網為研究對象,在總結國內外管網研究技術成果的基礎上,采取理論研究和實例分析相結合的方法,對節水灌溉管網水力計算和水頭損失計算方法進行了系統的研究。

關鍵詞：管網；流量；水力計算

農業用水是水資源的最大用戶，約占世界資源總量的70%，占國內水資源總量的88%，其中灌溉用水占農業用水的90%以上，而且隨著社會工業、農業用水的飛速發展和人民生活水平的不斷提高，水資源的供需矛盾越來越突出，因此，發展節水灌溉勢在必行。管網水力計算是管網設計的依據，因此，節水灌溉管網水力計算顯得尤為重要。中外學者對此做出了巨大貢獻，達西—維斯巴赫公式、哈森—威廉斯公式、謝才公式等都為管網的水頭損失計算解決了根本性問題。本文主要介紹樹狀管網和環狀管網水力計算的基本內容及其每項計算內容中不同情形對應的不同計算方法。

1　管網的水力計算

在給水工程中將許多管路組合成為管網，按其布置形式可將其分為樹狀管網和環狀管網兩種類型。

1.1管網要素之間的關系

管網要素包括節點、管段和環，這些要素組成管網。在管網中節點數J、管段P和環數L有以下關系：

P=J+L-1

對于一個環狀管網，有J-1個連續方程和L個能量方程，共有J+L-1個獨立方程，根據式（1）解這J+L-1獨立方程，剛好可求出P個管段流量，這J+L-1個獨立方程就構成了環狀管網水力計算基本方程。

1.2樹狀管網水力計算

1）已知管路沿線地形、水塔高度Ht、管路長度l、用水點的自由水頭Hz及通過的流量，要求確定管徑。

根據已知條件，算出它們各自的平均水力坡度：

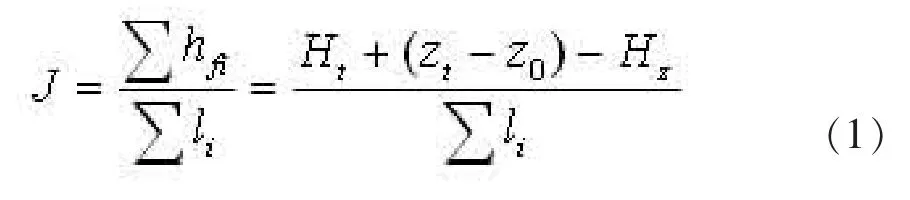
式中：Z0——控制點地面標高，m；

Zt——泵站或水塔處的地面標高，m；

Σhfi——從水塔到管網控制點的總水頭損失，m。

式中：Qmi——各管段流量，m3/s。

按照求得的Si值，結合經濟流速選擇各管段直徑。實際選用時，可取部分管段比阻率S大于計算值Si，部分小于計算值，使得這些管段的組合正好滿足在給定水頭下通過需要的流量。

干線管徑確定后，算出各節點的水頭，繼續設計各支線的管徑。

2）已知管路沿線地形，各管段長度l及通過的流量Q和端點要求的自由水頭HZ，要求確定管路的各段直徑d及水泵的揚程或水塔的高度Ht。

根據各段流量Q和經濟流速確定管道直徑d，依流量Q和直徑d及管長l計算出個管段的水頭損

選擇其中平均水力坡度最小的那根干線作為控制干線進行設計。控制干線上按水頭損失均勻分配，即各管段水力坡度相等的條件，由式hfi=SiliQmi計算各管段比阻率：失，然后按串聯管路計算干管中從水塔到管網控制點的總水頭損失。管網的控制點是指在管網中水塔至該點水位水頭損失、地形標高和要求自由水頭三項之和最大值的點。對于簡單樹狀管網，控制點可以直觀判斷；對于復雜樹狀管網，應通過計算比較確定。

對于水泵揚程或水塔高度Ht為：

式中：HZ——控制點要求的壓力水頭或工作水頭，m；

Z0——控制點地面標高，m；

Zt——泵站或水塔處的地面標高，m；

Σhfi——從水塔到管網控制點的總水頭損失，m。

1.3環狀管網水力計算

通常管網的布置及各管段的長度l和各節點流出的流量為已知，要求確定各管段通過的流量Q和管徑d，其中需要求出各管段水頭損失hf。

根據各節點流量求得各管段流量Q，再依經濟流速選擇各管段直徑d，計算各管段的水頭損失。環狀管網中的每一個環應按并聯管道考慮，在每一個環的水力計算中均有：

1）連續方程。環狀管網分配流量時，流入一節點的流量之和等于流出這一節點的流量之和，規定流出節點的流量為正，流入節點的流量為負，即在各節點上有：

2）能量方程。在任一閉合環路內，由某一節點沿兩支管流至另一節點的水頭損失應該相等，設在一個環內以順時針水流方向管段的水頭損失為正，逆時針為負，則

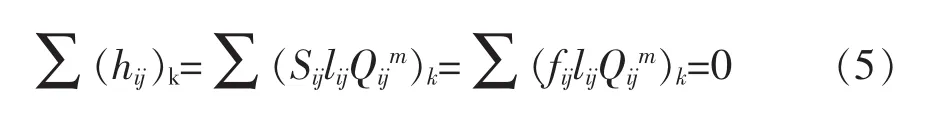
式中：Qij——管段流量，m3/s；

l——管道長度，m；

S——比阻率或比阻抗；

f——摩阻，f=Sl；

m—流量指數。

（3）環狀管網平差原理。在環狀管網水力計算中，可先根據連續方程初分流量，但初分流量很難滿足能量方程，為此，必須調整管段流量，以達到同時滿足連續方程和能量方程的目的，這里用校正流量△q來調整各個基環中的管段流量，調整后應不破壞節點連續方程，規定校正流量順時針方向為正，逆時針方向為負。

設Q為管段初分流量，基環的校正流量為△q，假設在初分流量的管段中，加入△q就可滿足能量方程：

上式中的每一個方程均表示調整流量后，該環各管段水頭損失的總和，△qi表示該管段所屬環的校正流量，對兩環的公共管段，應同時考慮兩個環的校正流量。

管段流量與校正流量方向相同則相加，否則相減，并由此計算各管段的新流量，如此反復調整管段流量，直到滿足能量方程為止。

4）校正流量計算公式。管網平差就是求解L個線性的△qi方程組，每一個方程表示一個環的校正流量，待求的是閉合差為零時的校正流量△qi。校正流量由兩部分組成:一是消除本環閉合差的校正流量；二是考慮鄰環影響的校正流量。如果忽略鄰環的影響，即每環調整流量時，不考慮鄰環的影響，這樣雖然計算精度有所降低，但計算簡單，對應的校正流量公式為：

式中：△hi——閉合差，環i內各管段水頭損失的代數和；

fij——摩阻，fij=Sijlij；

Qij——管段流量，m3/s；

m——流量指數，其值可查表得。

2　樹狀管網與環狀管網的比較

1）布置方式不同。

2）適用條件不同。樹狀管網一般只適用于沒有坡度或坡度比較平緩的地形；環狀管網適用即可使用于有坡度的地形也可使用于沒有坡度的地形。

3）造價不同。樹狀管網投資較省，環狀管網投資大。

4）供水可靠性不同。樹狀管網投資可靠性較差，環狀管網較好。

5）計算量不同。樹狀管網水力計算方便快捷，環狀管網水力計算復雜，計算過程量大。

6）水力計算步驟不同。

樹狀管網水力計算步驟：

（1）確定干管走向和水塔位置，然后在干管上選定節點并對節點編號；

（2）管段流量推算逐級進行，即從最末端開始逐段推算上一級管段的流量；

（3）根據管段設計流量和依經濟流速求得的管徑，不同的流態區域選擇不同的水頭損失計算公式，計算各個管段的水頭損失；

（4）以距二級泵站最遠或最高的點為控制點，根據控制點所需要的服務水壓求出水塔高度和水泵揚程。

環狀管網水力計算步驟：

（1）初擬各管段的水流方向（用箭頭標在圖上）并根據各節點上應滿足連續方程初擬各管段的流量；

（2）根據經濟流速和管段的流量選擇管徑；

（3）計算各管段水頭損失，校核各環是否滿足能量方程，如果Σhij≠0，其差值為第一次閉合差△hi，需管網平差；

（4）按校正流量計算公式計算校正流量，如果閉合差為正，校正流量即為負，反之則校正流量為正。

（5）按校正后的流量重新計算水頭損失，求閉合差，若不滿足精度要求，則再進行流量校正，某一環在第一次校正后還會受到相鄰另一環校正流量的影響，則：

式中：△qs——本環的校正流量，m3/s；

△qn——鄰環的校正流量,m3/s。

至此，再從第2步起重復計算，直到每環的閉合差在0.5m以下，此時各管段的管徑、流量、水頭損失就可作為最后結果。

3　結語

對于樹狀管網，確定了干管走向后逐級推算出管段流量，依經濟流速求管道直徑，選取適合的公式計算水頭損失，選擇控制點求得水塔高度和水泵安裝高程。對于環狀管網，需先進行初分流量，確定管徑后計算的水頭損失是否滿足能量方程，如不滿足需進行管網平差，直至每環的閉合差在0.5m以下。本文中外學者所研究的管網水力計算的方法大大推動了灌溉管網設計的理論發展和技術的應用，其中達西—維斯巴赫公式計算最精確，但工程量過大，本文將單項指數公式做成Excel表格，應用于實例中。隨著微型計算機的迅速發展，結合計算機的特點，將管網水力計算自動化，并有效地運用于實際工作中，有效提高灌溉管網工程設計效率和設計精度。

參考文獻:

[1]郝瑞霞，王海云.管網水力計算及其在給水工程中的應用[J].東北水利水電學報，2004，22（6）：22-24.

[2]呂宏興，裴國霞，楊玲霞.水力學[M].北京：中國農業出版社，2002，76-86.

[3]蘇德榮，田媛.微灌理論與實踐[M].甘肅：甘肅教育出版社，1988，42-43.

[4]王旭強，鄭魚洪.滴灌中的管網水力計算[J].浙江水利水電專科學校學報，2002，17(3):67-68.

[5]趙鳳橋.噴灌管網水力計算方法研究及軟件開發[M].北京：中國農業出版社,2003，82-83.

[6]趙振興，何建京.水力學[M].北京：清華大學出版社，2005，34-35.

[7]吳春占，張艷紅.城鎮供水管網水力計算方法[J].中國水運，2009，21（9）:33-34.

[8]羅固源，肖明奎.水力學[M].重慶：重慶大學出版社，2001，45-47.

[9]史濱海，田軍倉，劉慶華.灌溉排水工程學[M].北京：中國水利水電出版社，2006，142-144.

[10]張德林，王佳.水力學[M].鄭州：黃河水利出版社，2005, 71-72.

[11]李田，寧希南.水力計算圖表[M].北京：建筑工業出版社，2008，111-113.

[12]韓會玲，羅金耀，李靖.城鎮給排水[M].北京：中國水利水電出版社,2010，72-73.

[13]清華大學水力學教研組.水力學[M].北京：人民教育出版社，1980，201-202.

[14]武漢水利電力學院，華東水利學院.水力學[M].北京：人民教育出版社，1980,82-83.

[15]孫道宗.水力學[M].北京：中國水利水電出版社，1992, 63-64.

[16]丁新求.水力學基礎[M].北京：中國水利水電出版社，2002, 96-97.

[17]徐正凡.水力學[M].北京：高等教育出版社，1986,152-153.

中圖分類號：TU996.7+2