異地配置的雷達(dá)與電子支援措施航跡關(guān)聯(lián)

，

(海軍航空工程學(xué)院電子信息工程系， 山東煙臺 264001)

0 引言

雷達(dá)與ESM航跡關(guān)聯(lián)是雷達(dá)與ESM數(shù)據(jù)融合的前提，是對目標(biāo)進(jìn)行更有效定位、跟蹤和識別的必要條件。由于ESM屬于被動傳感器，僅有角度信息而沒有距離信息[1-3]，且主被動傳感器的數(shù)據(jù)率往往不一致，因而在雷達(dá)與ESM航跡關(guān)聯(lián)中存在很多的困難與不確定性。根據(jù)傳感器的相對位置不同，雷達(dá)與ESM航跡關(guān)聯(lián)問題可以分為同地配置與異地配置兩種情況[4]。同地配置的雷達(dá)與ESM航跡關(guān)聯(lián)問題研究得較早且成果豐碩[5-12]。通常是在極坐標(biāo)下利用角度量測構(gòu)造統(tǒng)計(jì)量，然后根據(jù)相應(yīng)的門限進(jìn)行關(guān)聯(lián)決策[5-7]。由于可利用的信息較少，所以需要較長的觀測時間和觀測樣本才能達(dá)到較好的關(guān)聯(lián)性能；或者對兩傳感器的量測進(jìn)行濾波處理，根據(jù)不同的濾波方法，可用的關(guān)聯(lián)向量也不同。通常運(yùn)用濾波后的狀態(tài)向量來進(jìn)行航跡關(guān)聯(lián)的性能比僅利用角度的方法好[7-12]，但是為了避免濾波器發(fā)散，要求被動傳感器根據(jù)目標(biāo)的運(yùn)動情況進(jìn)行一定的機(jī)動。

但是在實(shí)際應(yīng)用中，會經(jīng)常面臨雷達(dá)與ESM異地配置的情況[13-16]。文獻(xiàn)[15]提出了基于角度統(tǒng)計(jì)量和基于距離統(tǒng)計(jì)量的兩種方法，仿真表明基于距離統(tǒng)計(jì)量的關(guān)聯(lián)算法有相對較低的錯誤關(guān)聯(lián)概率，但正確關(guān)聯(lián)概率仍有待提高。本文首先利用雷達(dá)量測定義了ESM虛定位點(diǎn)；然后利用交叉定位點(diǎn)與ESM虛定位點(diǎn)來構(gòu)造距離統(tǒng)計(jì)量，根據(jù)相應(yīng)的門限進(jìn)行關(guān)聯(lián)判別；最后與文獻(xiàn)[15]的基于距離統(tǒng)計(jì)量的方法進(jìn)行了仿真對比，本文提出的方法取得了較好的關(guān)聯(lián)效果。

1 ESM虛定位點(diǎn)

如圖1所示，假設(shè)二維情況下兩部異地配置的雷達(dá)和ESM在公共笛卡爾坐標(biāo)系下同時對目標(biāo)進(jìn)行共同探測，其中雷達(dá)位于坐標(biāo)(xa,ya)處， ESM位于(xb,yb)處。雷達(dá)在k時刻量測由距離和方位角共同組成，且該量測受到隨機(jī)量測噪聲影響，則

(1)

(2)

圖1基于ESM虛定位點(diǎn)的雷達(dá)與ESM航跡關(guān)聯(lián)示意圖

圖1中交叉定位點(diǎn)是由k時刻兩個傳感器測得角度交叉定位得到，其直角坐標(biāo)為(x1(k),y1(k))：

(3)

定義ESM虛定位點(diǎn)，從幾何圖形直觀描述為：以ESM為圓心，各雷達(dá)量測到ESM的距離為半徑畫圓，與ESM角度方向的交點(diǎn)為ESM虛定位點(diǎn)，其直角坐標(biāo)為(x2(k),y2(k))，因此ESM關(guān)于目標(biāo)的虛距離為

(4)

所以

(5)

式中，(xr(k),yr(k))是雷達(dá)關(guān)于目標(biāo)的轉(zhuǎn)換直角坐標(biāo)：

(6)

2 基于ESM虛定位點(diǎn)的雷達(dá)與ESM航跡關(guān)聯(lián)算法

2.1 構(gòu)造關(guān)聯(lián)統(tǒng)計(jì)量

k時刻交叉定位點(diǎn)到ESM虛定位點(diǎn)的距離為

d(k)=sgn(y1(k)-y2(k))·d12(k)

(7)

式中，

所以

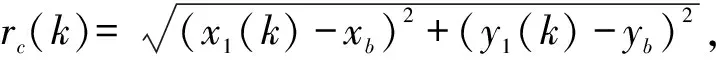
d(k)=rc(k)-rb(k)

(8)

從上式可以看出，d(k)是由ra(k),θa(k)和θb(k)確定，由于雷達(dá)的測距、測角和ESM的測角誤差相互獨(dú)立，服從高斯分布，所以式(8)可近似認(rèn)為服從零均值的高斯分布，其方差為

式中，

(10)

式中，各式中的偏導(dǎo)數(shù)如下:

(11)

(12)

(13)

(14)

2.2 關(guān)聯(lián)判決

得到基于距離統(tǒng)計(jì)量判別函數(shù)后，選擇適當(dāng)?shù)年P(guān)聯(lián)決策門限η，雷達(dá)與ESM的航跡關(guān)聯(lián)問題可以轉(zhuǎn)化為如下假設(shè)檢驗(yàn)問題：

H0：若Δ(n)>η，則判斷雷達(dá)與ESM航跡不關(guān)聯(lián)；

H1：若Δ(n)≤η，則判斷雷達(dá)與ESM航跡關(guān)聯(lián)。

當(dāng)給定允許的漏關(guān)聯(lián)概率為β時，決策門限η的選取應(yīng)使得雷達(dá)和ESM在實(shí)際關(guān)聯(lián)的情況下被錯誤判決為不關(guān)聯(lián)的概率小于β，即Pr{H0|H1}≤α。當(dāng)雷達(dá)和ESM航跡關(guān)聯(lián)時，由式構(gòu)造的距離統(tǒng)計(jì)量服從自由度為n的2分布。即

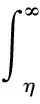
(15)

(16)

3 仿真分析

為了驗(yàn)證本文算法的有效性，用本文方法與文獻(xiàn)[15]的基于距離統(tǒng)計(jì)量的方法關(guān)聯(lián)性能進(jìn)行仿真對比實(shí)驗(yàn)。仿真中， 正確關(guān)聯(lián)概率為Ec=Nc/ (Nc+Ne+Ns)， 錯誤關(guān)聯(lián)概率為Ee=Ne/ (Nc+Ne+Ns)，漏關(guān)聯(lián)概率為Es=Ns/(Nc+Ne+Ns)，其中Nc,Ne和Ns分別為實(shí)驗(yàn)中正確關(guān)聯(lián)、錯誤關(guān)聯(lián)和漏關(guān)聯(lián)點(diǎn)跡對的數(shù)目，且有Ec+Ee+Es=1。

實(shí)驗(yàn)1：不同雷達(dá)測角誤差對算法的影響。假設(shè)雷達(dá)與ESM分別位于(0 km,0 km)和(100 km,0 km)， ESM的測角誤差為0.6°，雷達(dá)測距和測角誤差分別為1 000 m和0.1°～1.2°，允許的漏關(guān)聯(lián)概率為0.1。以(40 km,70 km)與(60 km,90 km)為對角的矩形作為公共觀測區(qū)域，隨機(jī)產(chǎn)生10個直線運(yùn)動目標(biāo)，目標(biāo)的初始速度和初始航向分別在50～70 m/s和0～2π內(nèi)均勻分布。在上述條件下進(jìn)行各100次蒙特卡洛仿真，圖2和圖3分別給出了不同雷達(dá)測角誤差時雷達(dá)與ESM航跡正確和錯誤關(guān)聯(lián)概率。

圖2 不同雷達(dá)測角誤差時雷達(dá)與ESM航跡正確關(guān)聯(lián)概率

圖3 不同雷達(dá)測角誤差時雷達(dá)與ESM航跡錯誤關(guān)聯(lián)概率

從圖2可以看出，隨著雷達(dá)測角誤差的增大，兩種方法的正確關(guān)聯(lián)概率呈逐漸減小趨勢，當(dāng)雷達(dá)測角誤差小于1.1°時，本文方法的正確關(guān)聯(lián)概率優(yōu)于文獻(xiàn)[15]的關(guān)聯(lián)算法。從圖3可以看出，隨著雷達(dá)測角誤差的增大，兩種方法的錯誤關(guān)聯(lián)概率呈逐漸增大趨勢，當(dāng)雷達(dá)測角誤差大于0.7°、小于1.1°時，由于文獻(xiàn)[15]的關(guān)聯(lián)算法具有較大的漏關(guān)聯(lián)概率，導(dǎo)致其正確關(guān)聯(lián)和錯誤關(guān)聯(lián)概率均小于本文方法。

實(shí)驗(yàn)2：不同雷達(dá)測距誤差對算法的影響。在其他條件同實(shí)驗(yàn)1完全相同的條件下，假設(shè)雷達(dá)測距誤差為200～2 000 m，雷達(dá)測角誤差為0.5°，分別進(jìn)行100次蒙特卡洛仿真，圖4和圖5分別給出了不同雷達(dá)測距誤差時雷達(dá)與ESM航跡正確和錯誤關(guān)聯(lián)概率。

圖4 不同雷達(dá)測距誤差時雷達(dá)與ESM航跡正確關(guān)聯(lián)概率

圖5 不同雷達(dá)測距誤差時雷達(dá)與ESM航跡錯誤關(guān)聯(lián)概率

從圖4可以看出，隨著雷達(dá)測距誤差的增大，兩種方法的正確關(guān)聯(lián)概率呈逐漸減小趨勢，當(dāng)雷達(dá)測距誤差較小時，現(xiàn)有方法的正確關(guān)聯(lián)概率大于本文的關(guān)聯(lián)方法，但是當(dāng)其大于600 m時，本文的關(guān)聯(lián)方法關(guān)聯(lián)效果更好。從圖5可以看出，隨著雷達(dá)測距誤差的增大，兩種方法的錯誤關(guān)聯(lián)概率呈逐漸增大趨勢，當(dāng)雷達(dá)測距誤差較大時，本文的關(guān)聯(lián)方法具有更低的錯誤關(guān)聯(lián)概率。

實(shí)驗(yàn)3：不同ESM測角誤差對算法的影響，在其他條件同實(shí)驗(yàn)1完全相同的條件下，假設(shè)ESM測角誤差為0.1°～1.2°，雷達(dá)測角誤差為0.5°，分別進(jìn)行100次蒙特卡洛仿真，圖6和圖7分別給出了不同ESM測角誤差時雷達(dá)與ESM航跡正確和錯誤關(guān)聯(lián)概率。

圖6 不同ESM測角誤差時雷達(dá)與ESM航跡正確關(guān)聯(lián)概率

圖7 不同ESM測角誤差時雷達(dá)與ESM航跡錯誤關(guān)聯(lián)概率

從圖6可以看出，隨著ESM測角誤差的增大，兩種方法的正確關(guān)聯(lián)概率呈逐漸減小趨勢，當(dāng)ESM測角誤差小于1°時，本文的關(guān)聯(lián)方法的正確關(guān)聯(lián)概率大于現(xiàn)有方法。從圖7可以看出，隨著ESM測角誤差的增大，兩種方法的錯誤關(guān)聯(lián)概率性能相當(dāng)，均呈逐漸增大趨勢。

實(shí)驗(yàn)4：不同目標(biāo)密集度對算法的影響，假設(shè)公共觀測區(qū)域的目標(biāo)數(shù)目為1～30，雷達(dá)測角誤差為0.5°，在其他條件同實(shí)驗(yàn)1完全相同的條件下分別進(jìn)行100次蒙特卡洛仿真，圖8和圖9分別給出了不同目標(biāo)數(shù)目時雷達(dá)與ESM航跡正確和錯誤關(guān)聯(lián)概率。

圖8 不同目標(biāo)數(shù)目時雷達(dá)與ESM航跡正確關(guān)聯(lián)概率

圖9 不同目標(biāo)數(shù)目時雷達(dá)與ESM航跡錯誤關(guān)聯(lián)概率

從圖8可以看出，隨著目標(biāo)數(shù)目的增大，兩種基于統(tǒng)計(jì)理論方法的正確關(guān)聯(lián)概率呈逐漸減小趨勢，本文的關(guān)聯(lián)方法的正確關(guān)聯(lián)概率始終大于現(xiàn)有方法。從圖9可以看出，隨著目標(biāo)數(shù)目的增大而增大，兩種方法具有類似的錯誤關(guān)聯(lián)概率。

4 結(jié)束語

本文研究了異地配置下的雷達(dá)與ESM航跡關(guān)聯(lián)問題，提出了利用ESM虛定位點(diǎn)與交叉定位點(diǎn)來構(gòu)造距離統(tǒng)計(jì)量的關(guān)聯(lián)算法，并與文獻(xiàn)[15]中基于距離統(tǒng)計(jì)量的關(guān)聯(lián)算法進(jìn)行了仿真對比。仿真結(jié)果表明，當(dāng)目標(biāo)數(shù)目相同時，本文提出的關(guān)聯(lián)方法在雷達(dá)測角誤差較小、雷達(dá)測距誤差較大或ESM測角誤差較小時具有更好的關(guān)聯(lián)性能；當(dāng)量測誤差相同，本文方法在不同的目標(biāo)密集程度時均有較好的關(guān)聯(lián)性能。

[1] 韓崇昭,朱洪艷,段戰(zhàn)勝,等. 多源信息融合[M]. 2版. 北京：清華大學(xué)出版社, 2010.

[2] 何友,王國宏,關(guān)欣,等. 信息融合理論及應(yīng)用[M]. 北京：電子工業(yè)出版社, 2010.

[3] 楊萬海. 多傳感器數(shù)據(jù)融合及其應(yīng)用[M]. 西安：西安電子科技大學(xué)出版社, 2004.

[4] 王國宏. 利用角度、角度變化率和ITG信息的主被動傳感器數(shù)據(jù)關(guān)聯(lián)[J]. 雷達(dá)科學(xué)與技術(shù), 2003, 1(1):39-45.

[5] WANG G H, MAO S Y, HE Y. Analytical Performance Evaluation of Association of Active and Passive Tracks for Airborne Sensors[J]. Signal Processing, 2003, 83(5):973-981.

[6] WANG G H, MAO S Y, HE Y, et al. Triple-Threshold Radar-to-ESM Correlation Algorithm When Each Radar Track is Specified by Different Number of Measurements[J]. IEE Proceedings:Radar, Sonar and Navigation, 2000, 147(4):177-181.

[7] 劉德浩,王國宏,陳中華. 基于EM-EKF的異類傳感器系統(tǒng)誤差配準(zhǔn)算法[J]. 雷達(dá)科學(xué)與技術(shù), 2011, 9(5):453-456.

LIU Dehao, WANG Guohong, CHEN Zhonghua. A Registration Algorithm of Different Sensors Based on EM-EKF[J]. Radar Science and Technology, 2011, 9(5):453-456.(in Chinese)

[8] 黃友澎,曹萬華,張志云,等. 基于灰色關(guān)聯(lián)分析的異類傳感器航跡相關(guān)算法[J]. 華中科技大學(xué)學(xué)報(bào)(自然科學(xué)版), 2011, 39(10):83-86.

[9] WANG G H, ZHANG X Y, TAN S C. Effect of Biased Estimation on Radar-to-ESM Track Association[J]. Journal of Systems Engineering and Electronic, 2012, 23(2):188-194.

[10] ZHOU Y F, MICKEAL J. A Sequential ESM Track Association Algorithm Based on the Use of Information Theoretic Criteria[C]∥10th International Conference on Information Fusion, Quebec:IEEE, 2007:1-7.

[11] 龍海鷹,任清安. 空管異類傳感器數(shù)據(jù)融合算法研究[J]. 雷達(dá)科學(xué)與技術(shù), 2010, 8(6):526-531.

[12] GUAN X, HE Y, YI X. Gray Track-to-Track Correlation Algorithm for Distributed Multitarget Tracking System[J]. Signal Processing, 2006, 86(11):3448-3455.

[13] 李彬彬,馮新喜,王朝英,等. 異類傳感器三維空間數(shù)據(jù)關(guān)聯(lián)算法研究[J]. 宇航學(xué)報(bào), 2011, 32(7):1632-1638.

[14] 王妍妍. 基于GAM模型雷達(dá)與ESM數(shù)據(jù)關(guān)聯(lián)實(shí)現(xiàn)方法[J]. 指揮信息系統(tǒng)與技術(shù), 2012, 3(3):40-43.

[15] 王國宏,邵錫軍,潘哲. 主被動傳感器異地配置下的數(shù)據(jù)關(guān)聯(lián)[J]. 現(xiàn)代雷達(dá), 2003, 25(4):26-29.

[16] 宋振宇,張翔宇,張光軼. 系統(tǒng)誤差對異地配置的雷達(dá)和ESM航跡關(guān)聯(lián)的影響[J]. 電光與控制, 2014, 21(3):42-46.