空管一次雷達抗風電場干擾目標檢測方法

， ，

(1.中國人民解放軍95483部隊， 四川成都 610054；2.中國人民解放軍93897部隊， 陜西西安 710077；3.中國人民解放軍94326部隊， 山東濟南 250023)

0 引言

風力作為一種綠色能源越來越受到人們重視，目前我國的風力發電裝機容量已經達到9.637×107kW。與此同時，風電場對雷達目標檢測的干擾也開始受到了人們的重視，而國產空管雷達的發展[1]也使風電場干擾成為一個必須直面的問題。文獻[2-3]研究了風電場對雷達探測的影響，指出風電場會引起虛警率上升、雷達盲區、目標丟失、航跡偏離等問題。文獻[4-7]研究了風力發電機的RCS模型及回波信號模型，并將仿真結果與實測結果進行了對比，對比發現，風力發電機的雷達回波具有一定的周期性，回波形式主要受旋翼個數、旋轉周期等影響。電磁波受到風輪機調制后，回波具有一定的頻譜寬度，而空管一次雷達常用MTD濾波器組來濾除雜波，提取有用的目標信號，但風輪機回波往往會擴展到0號濾波器(低通濾波器)外，MTD后進行恒虛警率(Constant False Alarm Rate, CFAR)處理會形成虛警。

加拿大雷聲公司最早將風電場抗干擾處理應用到實際雷達裝備中[8]，在其ASR-10/23SS空管一次雷達中采用了檢測前、檢測、檢測后三步的處理方式，這是一種較實用的抗風電場干擾方法，但文獻僅給出了總體介紹，未提供詳細算法。Uysal等人在2014年國際雷達會議上提出了一種基于信號分解的風輪機雜波消除算法[9]，該算法利用形態成分分析(Morphological Component Analysis, MCA)將風輪機雜波與飛行器目標回波疊加信號進行了分離，但該算法計算較復雜且需要較長時間積累。Karabayir等人則在2015年國際雷達會議上提出一種基于CLEAN算法的風輪機雜波消除算法[10]，通過構造僅包含風輪機回波的輔助雷達距離維波形，將雷達接收回波信號減去該輔助信號以獲得不包含風輪機回波的新信號，但該算法沒有考慮風輪機雷達回波的不穩定性。

針對上述情況，根據飛行器及風輪機的雷達回波模型，提出了一種基于目標識別的抗風電場干擾目標檢測方法，將風電場干擾抑制問題轉化為飛行器目標與風輪機目標的識別問題，通過對回波信號的目標特性判斷，剔除風輪機回波，保留飛行器目標回波。仿真表明該方法可以有效地完成飛行器目標回波與風輪機回波的辨別，保證飛行器目標在風電場雜波中航跡的連續性及準確性。

1 問題描述及數據模型

空管一次雷達為了實現對飛行器目標的自動檢測、自動跟蹤，往往采用MTD與CFAR結合的技術，在濾除固定物雜波后進行目標的恒虛警檢測。風輪機隨風轉動后，照射的電磁波在反射后會產生多普勒頻移，當這些信號進入MTD濾波器組的非0號濾波器時，就可能引起虛警；同時風輪機作為強反射體，產生強回波后會整體提高CFAR門限，影響飛行器目標的檢測，產生陰影效應[8]。為了防止風電場雜波區成為雷達探測的“空洞”，則需要相應的算法完成風電場雜波區中風輪機回波的抑制及飛行器目標回波的檢測。本文中考慮降低CFAR門限，使飛行器及風輪機回波都通過CFAR處理，但對通過CFAR門限的回波進行目標識別，判定其為飛行器或風輪機，將原問題轉化為目標識別問題。這里先給出不同種類飛行器(渦扇、螺旋槳以及直升機)和風輪機的雷達回波模型。

飛行器目標的雷達回波包含機身回波、旋轉部件回波(JEM分量)和噪聲分量部分，綜合表示[11]為

sAC(t)=as(t)[Cf_ACSf_AC(t)+CJEM_ACSJEM_AC(t)]+

Cnwn(t)

(1)

式中，as(t)為雷達系統對目標回波的總限制；Sf_AC(t)，SJEM_AC(t)和wn(t)分別為機身分量、旋轉部件分量和噪聲分量；Cf_AC，CJEM_AC和Cn為各分量的系數。具體地，機身回波分量為

Sf_AC(t)= exp(j2πfdt)

(2)

JEM回波分量為

(3)

式中，fd為機身多普勒頻移量，λ為雷達波長，R0為目標遠場距離，α為方位角，β為俯仰角，L1m和L2m分別為槳葉根和槳葉尖到槳中心的距離，M為理想旋轉部件數量(發動機數量)，可見度函數V(α,β′,P)用來描述旋轉部件遮擋情況，Nm為第m個旋轉部件的葉片數，θkm=θ0+2πk/Nm，θ0為第0個槳葉的初始轉角，一般忽略整個槳葉的扭轉，g1m=sin(|β′| +?m)+sin(|β′|-?m) ，g2m=sign(β′)[sin(|β′|+?m)+sin(|β′|-?m)]，?m表示漿葉角，β′用于區別旋轉面方向，當旋轉面平行飛行方向時β′=β， 垂直時β′=π/2-β，ωrm為第m個旋轉部件的轉速。

風輪機回波模型與飛行器目標模型類似，但風輪機為固定目標，所以沒有整體目標的多普勒頻移項fd，同時去掉了一些考慮不同飛行器類型而設置的參數。其常用回波模型[5,7]如下：

sWT(t)=as(t)[Cf_WTSf_WT(t)+CJEM_WTSJEM_WT(t)]+

Cnwn(t)

(4)

式中：Sf_WT(t)，SJEM_WT(t)和wn(t)分別為風輪機塔分量、風輪機葉片分量和噪聲分量；Cf_WT，CJEM_WT和Cn為各分量的系數。具體地，風輪機塔為固定物，回波僅包含距離調制：

(5)

風輪機葉片回波分量為

cos(γ)sin(θi)sinc(δi)

(6)

式中，A為系數，M為分辨單位中的風輪機個數，Ni為第i個風輪機的頁片數，Li為槳葉長度，γ為雷達波束方向與風輪機旋轉面的夾角，θi=ωit+2πn/Ni+θ0，ωi為轉速，δi=(2πLi/λ)cos(α)· cos(γ)cos(θi)，其他符號與之前飛行器模型中相同的符號代表相同含義，兩個模型中各角度參數的具體含義可以參看文獻[5,11]中圖示。

在目標識別時，除了利用飛行器機身回波與風輪機回波特征進行識別外，還可以利用JEM特征提高識別的正確率。4種類型目標的典型JEM信號頻譜如圖 1所示，可以看出4種目標的JEM回波分量頻率特性有較大區別。但實際應用中，空管雷達無法長時間照射目標，時間一般在20～100 ms，使得多普勒域的分辨率較低，簡單的頻域進行比較識別率較低，需要采用特征提取來進一步識別。

(a)渦扇飛機

(d)風輪機圖14種目標JEM回波分量的典型頻率特性(雷達頻率為2.6 GHz，RPF=3 kHz，采樣時間為1 s，前3種目標帶有一定的整體多普勒頻移)

2 目標檢測方法

本文提出的目標檢測方法總體步驟如下：

第一步空管雷達是固定配置，所以雷達工作范圍內的風電場區域信息比較容易獲得。為防止風輪機強回波提高CFAR門限，使得飛行器目標漏檢，可根據相關信息在雷達中設置相應的距離方位波門圖(RAG圖)，以降低CFAR門限。實際處理中，可在該區域設置航跡禁止起始區，當預測無飛行器通過該區域時，區域內的目標點都按風電場雜波處理，降低數據處理量。這一步是常規設置，數據處理從第二步開始。

第二步對可能進入風電場區域的目標作目標識別處理，區分渦扇飛機、螺旋槳飛機及直升機，而低分辨雷達對飛行器目標識別當前已有較多算法可供參考[11-13]，本文不作進一步討論。這一步是為了后續有效利用不同飛機器的JEM信息，提高風電場區域內目標識別的準確率。

第三步對風電場區域內的雷達信號進行MTD及CFAR處理，提取可能的目標，對超過CFAR門限并且處于航跡預測的波門內的目標進行飛行器與風輪機目標識別，具體算法見后文。將目標識別結果送給數據處理器進行相關處理，剔除風電場干擾。

因為第二步已經完成了飛行器類型的識別，所以第三步完成的是特定飛行器類型與風輪機的識別(例如，第二步中飛行器識別為直升機，那么第三步就只需要就直升機與風輪機進行識別)。為了提取不同目標的特征進行識別，就目標的頻域特性進行分析。首先考慮回波信號頻域的集中性，即集中大部分能量的頻率點的多寡。這里采用頻率能量熵[13]來作為提取特征1。首先將信號變換到頻域并求模值：

M1(f) = |FFT(s(t))|

(7)

式中， FFT(·)為快速傅里葉變換， |·|為求模運算。

定義特征1：

(8)

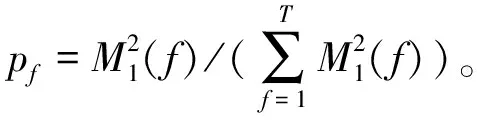
為了更好地利用目標的JEM特性，需要先去除機身回波，并保留JEM回波。對飛行器而言，機身回波強度大于JEM回波，且如式(2)所示，僅有單一頻率，所以可以通過找到頻域中模值最大點的方法來去除，這也就是常用的CLEAN算法[14]。而對風輪機而言，JEM回波所占頻點較多，剔除其中一點并不會明顯影響其頻率特征。CLEAN算法的簡要步驟[13]如下：

第一步對回波信號s作快速傅里葉變換，S=FFT(s)。

第二步搜索找到S中模值最大的點，計算該點的頻率f1、幅度ρ1及相位φ1。則機身回波為

(9)

式中 ，t=1,2,…,T。

第三步將回波信號減去機身回波，得到JEM回波信號：

sJEM(t) =s(t)-sF(t)

(10)

對CLEAN運算得到的sF(t)和sJEM(t)，從中提取了兩個特征量。

定義特征2：

F2= entropy(MJEM)

(11)

式中，MJEM為sJEM(t)的快速傅里葉變換結果求模值。該值反映了目標JEM回波的頻域能量特征。

定義特征3：

F3= ‖sF‖2/‖sJEM‖2

(12)

式中， ‖·‖表示l2范數，該特征代表了目標機身回波能量與JEM回波能量的比值。

典型條件下，4種目標3種特征值的概率分布曲線如圖 2所示。可以看出，4種目標3個特征的概率分布都存在重疊，無法由一種特征完成識別；但又各有區別，所以可以用來共同實現目標識別的功能。

(a)特征1

(b)特征2

(c)特征3圖2 典型條件下4種目標3種特征值的概率分布曲線(雷達頻率為2.6 GHz，RPF=3 kHz，采樣時間為50 ms，詳細仿真條件參見第3節)

支撐向量機(Support Vector Machine, SVM)方法是模式識別常用的算法之一，本文采用高斯核的SVM來完成目標的識別，先使用不含噪聲信號樣本來完成對分類器的訓練，輸出3種針對不同飛行器類別的分類器，最后對輸入帶有噪聲的測試信號完成分類。算法流程如圖 3所示，圖示上半部分為分類器訓練過程，下半部分為樣本分類過程。因為在總的算法第二步中已經完成了飛行器的識別，所以實際下半部分的三路中只有對應飛行器的一路在進行處理。

圖3 飛行器與風輪機目標識別算法框圖

3 仿真實驗及分析

仿真實驗中，設置雷達工作頻率為2.6 GHz，脈沖重復頻率PRF=3 kHz。飛行器參數參考文獻[13]設置，如表 1所示，其中渦扇飛機6種，螺旋槳飛機8種，直升機10種，飛機序號分別以T,P及H開頭表示。仿真中各飛行器的飛行速度、距離及高度參考文獻[11]設置，如表 2所示。此外，式(3)中V(α,β′,P)設為常數，方位角α及槳葉初相角θ0在U(0,π)隨機取值，式(2)中機身回波幅度Cf_AC在一次照射時間內保持不變，不同照射組間服從Rayleigh分布，以符合SwerlingⅠ類起伏模型。風輪機參數參考文獻[5]設置，式(6)中風輪機數M設為1，槳葉數Ni設為3，轉速在U(5,25)(r/min)中均勻概率取值，風輪機槳葉長度在U(10,24)(m)中均勻概率取值，方位角α及槳葉初相角θ0在U(0,π)隨機取值，因風輪機高度都很低，在距離R0足夠大時，俯仰角隨R0改變很小，所以R0設為常數。

在每次仿真實驗中，每組數據使用飛行器序號隨機抽取，4種目標先分別產生1 000組無噪回波數據用于分類器訓練；然后再分別產生1 000組包含高斯白噪聲的回波數據用于測試，即每個分類器的訓練數據與測試數據都為2 000組(1 000組飛行器加1 000組風輪機)。

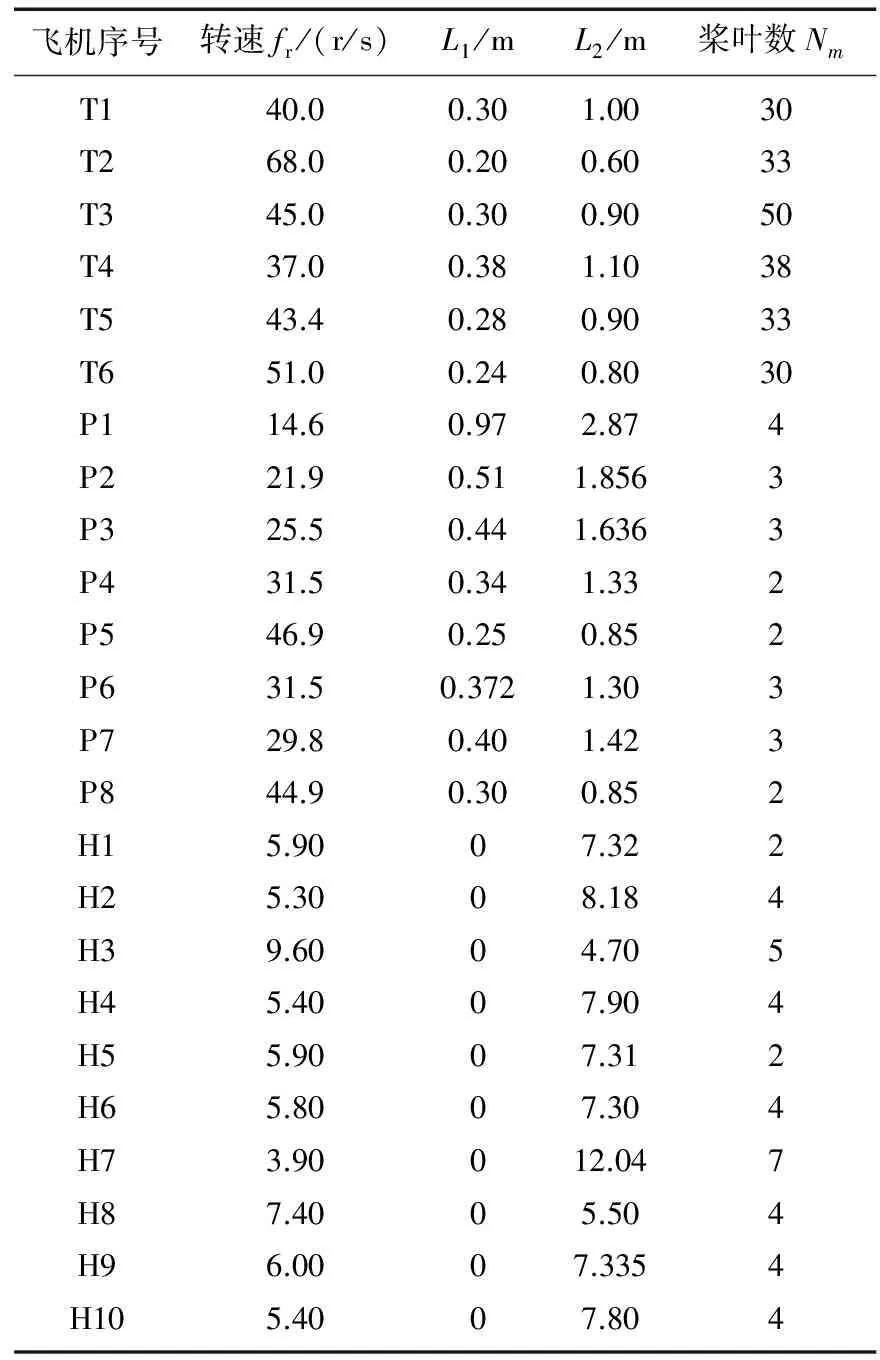
表1 3種飛行器旋轉部件轉速和結構參數

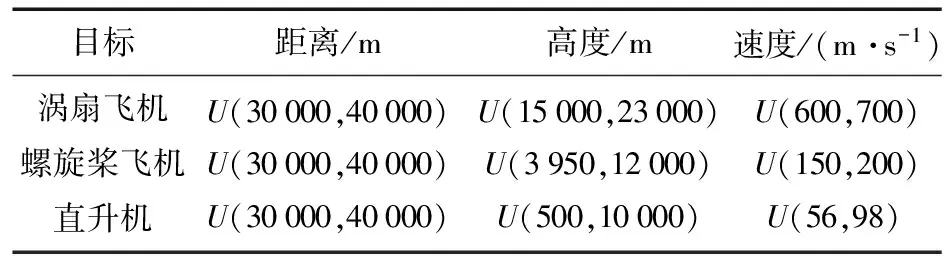
表2 3種飛行器典型場景下參數分布(U(a,b)代表(a,b)上均勻分布)

仿真實驗1：總體性能及不同SNR對檢測準確率的影響

設置照射時間為50 ms，3種分類器的檢測準確率如圖4所示。可以看出，當信噪比(SNR)高于10 dB時，3種飛行器都可以很好與風輪機進行區分，能夠完成風電場中飛行器與風輪機回波的區分工作。此外，SNR低時，渦扇飛機與風輪機的識別準確率較高，因為渦扇飛機JEM回波特征較簡單，抗噪聲干擾能力較強。而隨著SNR升高，另兩種飛行器的識別準確率提升，因為這兩種目標的JEM回波特征較復雜，SNR高時更容易與風輪機的JEM回波特征進行區分。

圖4不同SNR下3種分類器的檢測準確率及平均檢測準確率

仿真實驗2：不同照射時間對檢測準確率的影響

設置SNR為15 dB，3種分類器的檢測準確率如圖5所示。可以看出，當SNR較高時，照射時間為20 ms即可以得到較良好的檢測性能，當照射時間超過30 ms后，檢測正確率緩慢提高但不明顯。此外，對直升機與風輪機進行區分，其準確率相對照射時間不敏感。

圖5不同照射時間下3種分類器的檢測準確率及平均檢測準確率

4 結束語

本文將風電場干擾抑制轉化為了飛行器與風輪機的目標識別問題，通過提取4種目標的整體特征及JEM回波特征，完成了對飛行器目標與風輪機干擾的區分。最后通過仿真實驗驗證了這種算法的有效性。在實際應用中，算法第三步可以不直接進行風輪機雜波的剔除，而是將檢測目標的信息與判定結果一起發送給后續的點跡、航跡濾波，進一步提高檢測的準確率。此外，本文沒有考慮地雜波及低SNR下算法的修正，后續工作可以就地雜波及噪聲的預濾除進行研究。

[1] 牛忠文,任翠鋒,鞠金山,等. 大口徑高精度航管雷達天線結構設計與應用[J]. 雷達科學與技術, 2015, 13(1):103-108.

NIU Zhongwen, REN Cuifeng, JU Jinshan, et al. The Design and Application of the Large-Diameter and High-Precision ATC Antenna[J]. Radar Science and Technology, 2015, 13(1):103-108.(in Chinese)

[2] SANTOS R M, CORREIA L M, ALVES C, et al. Analysis of Wind Turbines Generators Influence in Aeronautical Radars[C]∥IEEE Antennas and Propagation Society International Symposium, Memphis, TN:IEEE, 2014:711-712.

[3] GREVING G, BIERMANN W D, MUNDT R. Wind Turbines as Distorting Scattering Objects for Radar:Visibility, Desensitization and Shadowing[C]∥13th International Radar Symposium, Warsaw:IEEE, 2012:275-277.

[4] KENT B M, HILL K C, BUTERBAUGH A, et al. Dynamic Radar Cross Section and Radar Doppler Measurements of Commercial General Electric Windmill Power Turbines Part 1:Predicted and Measured Radar Signatures[J]. IEEE Antennas and Propagation Magazine, 2008, 50(2):211-219.

[5] MISHRA K V, CHANDRASEKAR V. Signal Analysis and Modeling of Wind Turbine Clutter in Weather Radars[C]∥IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI:IEEE, 2010:3561-3564.

[6] LOK Y F, PALEVSKY A, WANG J, et al. Simulation of Radar Signal on Wind Turbine[J]. IEEE Aerospace and Electronic Systems Magazine, 2011, 26(8):39-42.

[7] KARABAYIR O, YUCEDAG S M, COSKUN A F, et al. Wind Turbine Signal Modeling Approach for Pulse Doppler Radars and Applications[J]. IET Radar, Sonar and Navigation, 2015, 9(3):276-284.

[8] SERGEY L. HUBBARD O, DING Z, et al. Advanced Mitigating Techniques to Remove the Effects of Wind Turbines and Wind Farms on Primary Surveillance Radars[C]∥IEEE Radar Conference, Rome:IEEE, 2008:1-6.

[9] UYSAL F, PILLAI U, SELESNICK I, et al. Signal Decomposition for Wind Turbine Clutter Mitigation[C]∥IEEE Radar Conference, Cincinnati, OH:IEEE, 2014:60-63.

[10] KARABAYIR O, UNAL M, COSKUN A F. CLEAN Based Wind Turbine Clutter Mitigation Approach for Pulse-Doppler Radars[C]∥IEEE Radar Conference, Arlington, VA:IEEE, 2015:1541-1544.

[11] 陳鳳,劉宏偉,杜蘭,等. 基于特征譜散布特征的低分辨雷達目標分類方法[J]. 中國科學：信息科學, 2010, 40(4):624-636.

[12] MOLCHANOV P, EGIAZARIAN K, ASTOLA J, et al. Classification of Aircraft Using Micro-Doppler Bicoherence-Based Features[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(2):1455-1467.

[13] DU Lan, WANG Baoshuai, LI Yanbing, et al. Robust Classification Scheme for Airplane Targets with Low Resolution Radar Based on EMD-CLEAN Feature Extraction Method[J]. IEEE Sensors Journal, 2013, 13(12):4648-4662.

[14] TSAO J, STEINBERG B D. Reduction of Sidelobe and Speckle Artifacts in Microwave Imaging:The CLEAN Technique[J]. IEEE Trans on Antennas Propagation, 1988, 36(4):543-556.