具有庇護所效應的Kolmogorov型捕食-食餌系統的進一步研究
林琳,馮曉梅
(1.運城農業職業技術學院 基礎教學部,山西 運城 044000;2.運城學院 應用數學系,山西 運城 044000)
具有庇護所效應的Kolmogorov型捕食-食餌系統的進一步研究
林琳1,馮曉梅2
(1.運城農業職業技術學院 基礎教學部,山西 運城 044000;2.運城學院 應用數學系,山西 運城 044000)
研究了一類具有庇護所效應的Kolmogorov型捕食-食餌系統,運用Bendixson環域定理及丁蓀紅定理,得到了該系統存在唯一極限環的充分條件.運用Dulac函數法,得到了系統不存在極限環的充分條件.同時利用Matlab進行了仿真.
庇護所效應;捕食者;食餌;平衡點;穩定性;極限環
近年來,食餌具有庇護所效應的捕食系統已被許多人所研究,取得了比較好的成果[1-7],但對于Kolmogorov模型[8]的研究成果還不甚多見.文獻[9]以Kolmogorov模型為基礎,創建了一類具備庇護所效應的2種群食餌-捕食系統,本文在此系統基礎上對其進行更深入的研討.
1 數學模型的建立
文獻[9]基于一系列的假設得到了模型
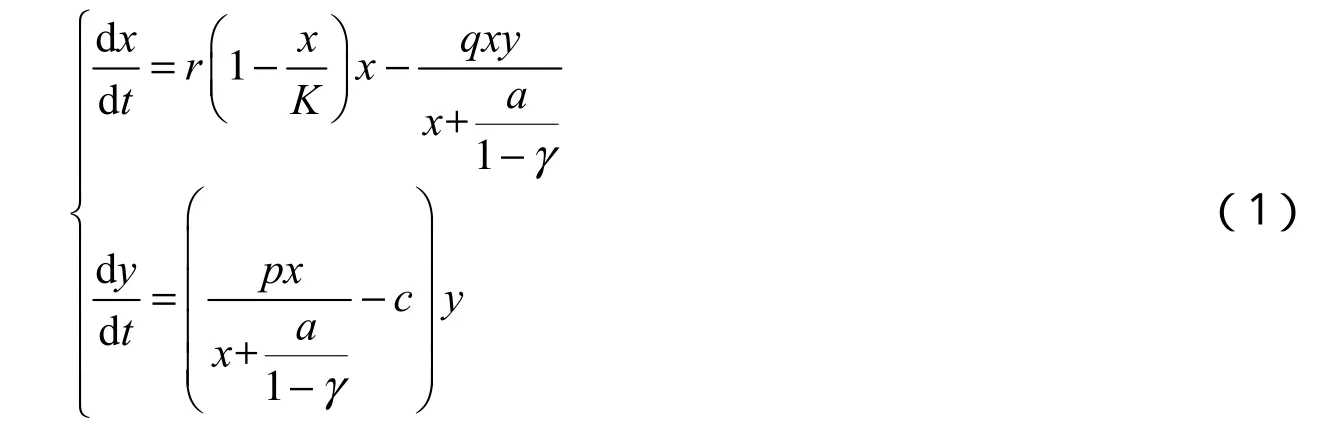
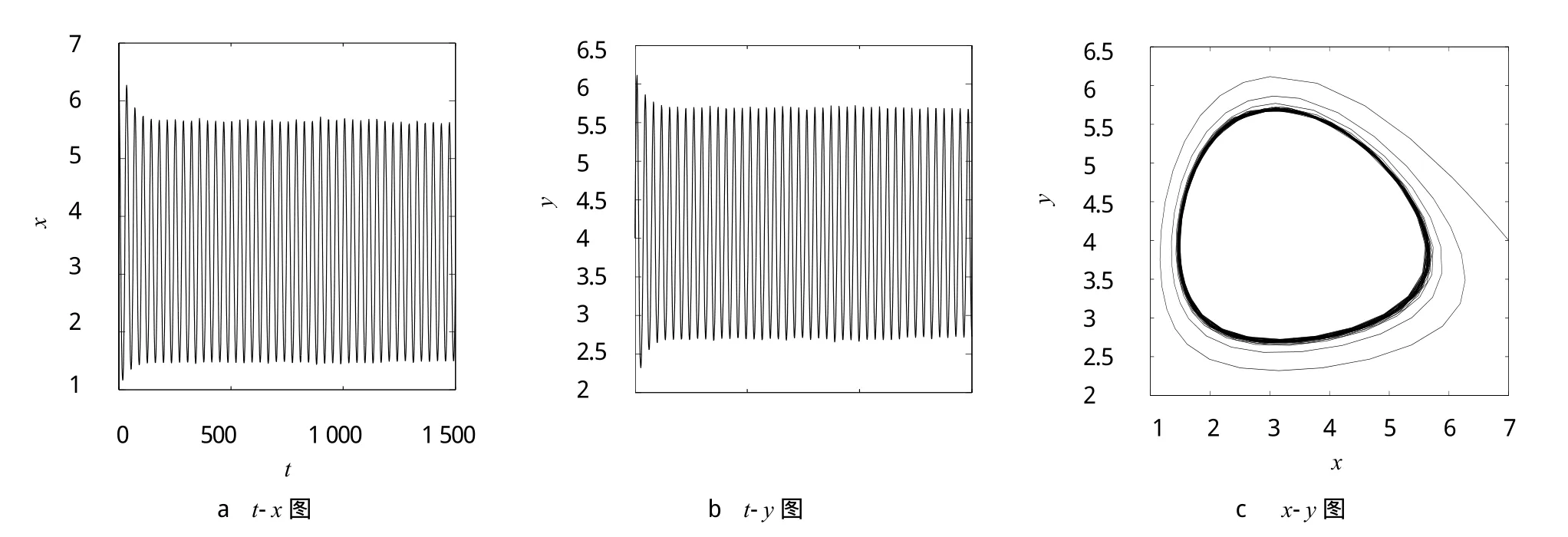
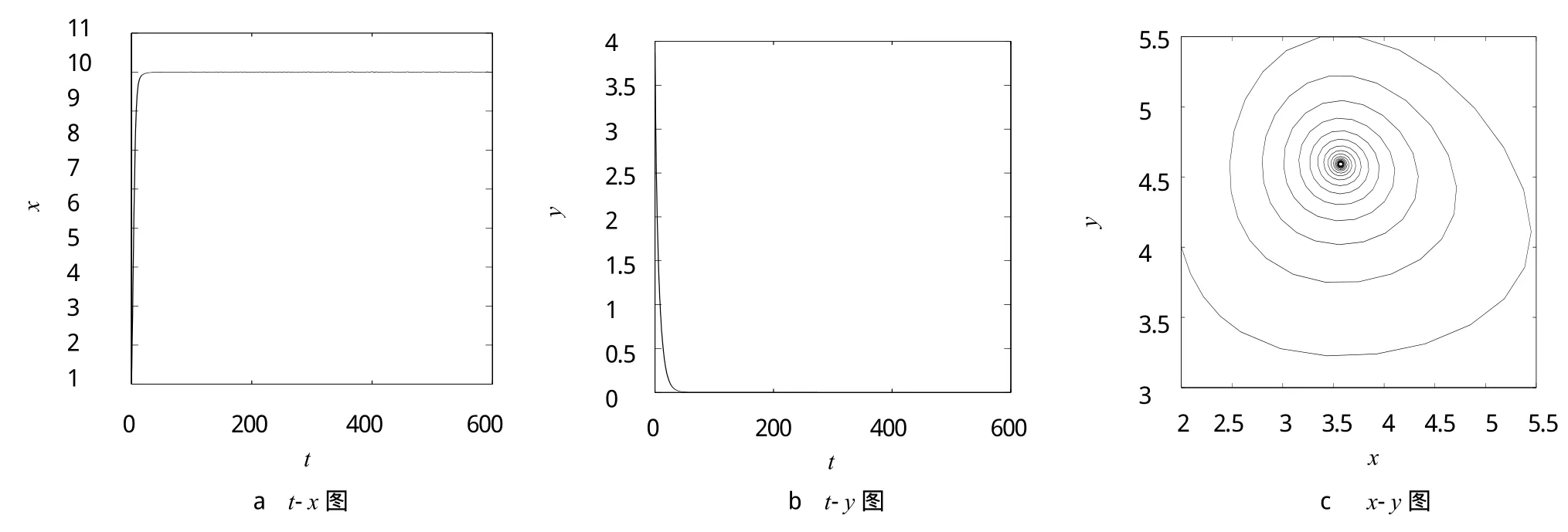
其中:x(t)為食餌種群在t時刻的種群密度;y(t)為捕食者種群在t時刻的種群密度;r為食餌種群固有的增長率;c為捕食者種群的死亡率;K為環境的容納量;q為捕食者最大消耗率;p(c 當1?C?AC>0時,系統(2)共有3個非負平衡點:,其中: 文獻[9]用常微分方程定性理論給出了系統(2)的平衡點類型及解的有界性.本文對此系統進行更深一步的研究. 定理1 設(A,C)∈,那么 為了更加明確地驗證定理2的正確性,對系統(1)的一個具體例子進行數學模擬,用數形結合的方法驗證其正確性. 令r=q=a=0.5,K=10,p=0.4,c=0.2,得到系統 圖1γ=0.84<γ1=0.85時的數值模擬 圖2γ1=0.85<γ=0.86<γ2=0.95時的數值模擬 圖3γ2=0.95<γ=0.99時的數值模擬 [1]林琳,侯林潔.具有庇護所的Lotka-Volterra型的捕食-食餌系統[J].北華大學學報:自然科學版,2012,13(1):19-21 [2]周稻祥,朱長榮.一類具有常數避難所與收獲率的捕食-食餌模型的穩定性[J].重慶理工大學學報:自然科學版,2012,26(12):122-126 [3]帥智圣,苗春梅,張偉鵬,等.具有庇護所的三種群捕食者-食餌模型[J].生物數學學報,2004,16(1):65-71 [4]徐昌進,陳大學.具有時滯的食餌-捕食模型的分支問題[J].重慶師范大學學報:自然科學版,2011(3):43-48 [5]徐國明,賈建文.一類具有避難所的捕食系統的分析[J].陜西師范大學學報,2007,21(4):4-7 [6]張艷波,王萬雄,段永紅.一類具第三類功能反應且食餌具有避難所的捕食系統的分析[J].數學的實踐與認識,2010,40(24):149-154 [7]馬智慧,李文龍,李自珍,等.具有已感染者庇護所效應的傳染病模型[J].蘭州大學學報,2008,44(2):111-114 [8]陳蘭蓀.數學生態學模型與研究方法[M].北京:科學出版社,1988 [9]林琳,雒志學.具有庇護所的Kolmogorov型的捕食-食餌系統[J].重慶理工大學學報:自然科學版,2014,28(2):120-122 [10]馬知恩,周義倉.常微分方程定性與穩定性方法[M].北京:科學出版社,2001 [11]丁蓀紅.捕食者-食餌系統極限環的唯一性[J].科學通報,1985(13):976-979 The further study of the Kolmogorov predator-prey system with prey refuges LIN Lin1,FENG Xiao-mei2 Studies the Kolmogorov prey-predator system with prey refuges.The sufficient condition for the existence and the unique of the limit cycle is given by using the Bendixson and Ding Sunhong theory.The sufficient condition that the system has no limit cycle is obtained by the Dulac function.The theory is illustrated by using the Matlab. prey refuge;predator;prey;equilibrium point;stability;limit cycle O175.1:Q141 A 10.3969/j.issn.1007-9831.2016.12.001 2016-10-13 國家自然科學基金資助項目(11501498) 林琳(1983-),女,山西運城人,講師,碩士,從事生物數學研究.E-mail:15835988676@163.com 1007-9831(2016)12-0001-05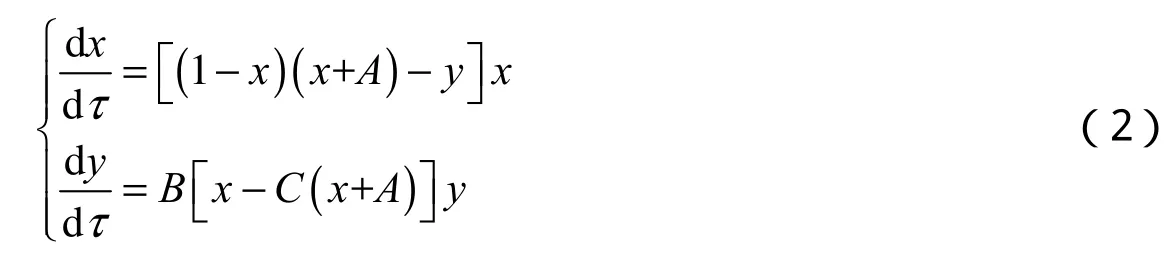
2 主要結果及證明


3 實例仿真
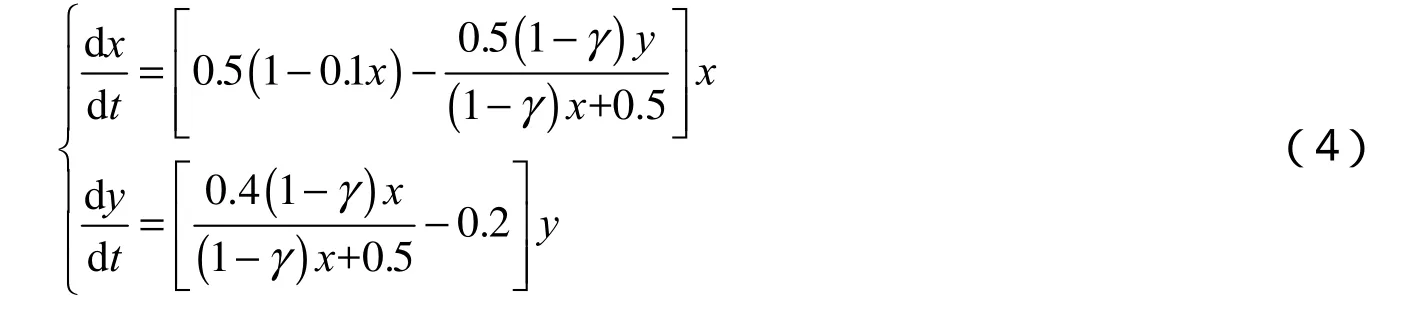

(1.Department of Primary Education,Yuncheng Polytechnic College of Agriculture,Yuncheng 044000,China;2.Department of Applied Mathematics,Yuncheng University,Yuncheng 044000,China)

